Statistical Independence Two events are statistically independent if

Statistical Independence • Two events are statistically independent if the probability of any one of them is unaffected by the occurrence of the other. • Independence can ordinarily be assumed from the nature of the random experiment For instance, consider Experiment 1 involving separate tosses of two fair coins, a dime and a quarter.

Statistical Independence • The assumed statistical independent events: -head of the dime (Hd) -head for the quarter (Hq) • For Experiment 2, (which has a statistically dependent events), the dime is tossed first. If head is obtained (Hd), a fair quarter is tossed. But, if tail is obtained (Td), a crooked twoheaded quarter is tossed instead.

Statistical Independence Pr[Hq] = ½ , when Hd occurs Pr[Hq] = 1 when Td occurs and Pr[Hq] = 3/4, in any repetition of the experiment

The Multiplication Law for Independence Event • Just to remind you that for independents events, one outcome is not dependent to occurrence of the next outcome. • The second basic law (multiplication law) of probability is intended for computing joint probabilities. • Pr[A and B] = Pr[A] X Pr[B]

The Multiplication Law for Independence Event • To illustrate, suppose a perfectly balanced coin id fairly tossed twice in succession. • H 1, T 1, H 2, T 2 are the events • Probability of two heads is the probability of the joint event H 1 and H 2 • Pr[H 1 and H 2] = Pr[H 1] X Pr[H 2] =½X½=¼

An Example • Among 24 invoices prepared by a billing department, 4 contain errors while the others do not. If we randomly check 2 of these invoices, what are the probabilities that (a) both will contain errors (b) neither will contain an error

Solution (a) The probability of getting an error on the first draw is 4/24 As we pick only 2 invoices and want to have error in both invoices, so after the first pick (with error), we have only 23 invoices left. And the among those 23 invoices only 3 invoices could have errors. So, the probability of the second event (picking an invoice with error in second draw) is 3/23. The probability that both will contain error is 4/24 X 3/23 = 1/46 = 0. 0217

Solution (b) The probability that neither will contain error is: 20/24 X 19/23 = 95/138 = 0. 688.

Conditional Probabilities • Consider how the probability value of one event is affected by the occurrence of another • A probability value computed under the assumption that the another event is going to occur is a conditional probability.

An Example It is more likely to rain tomorrow if there is a solid cloud cover than if there are patches of blue. For the events “rain” and “blue patches”, the following value might apply: Pr[rain|blue patches] = 0. 30 The event “rain” is listed first, and. 30 is the conditional probability of that event; the condition - given event – “solid overcast” is listed second, and the vertical bar is a shorthand representation for “given that”. Should no stipulations be made regarding sky conditions. We might have Pr[rain] = 0. 20 which is unconditional probability

Conditional Probability • It may be possible to compute a conditional probability directly from known probability values using the following:

The General Multiplication Law Suppose that a quality-control inspector has established that 10% of all electric assemblies fail (F) the circuit test. Twenty percent of the failing items have poor (P) solder joints. This experience provides that the following particular assembly will fail and have poor solder joints: Pr[F] = 0. 10 Pr[P|F] = 0. 20 The multiplication law gives the joint probability that a particular assembly will fail and have solder joints Pr[F and P] = Pr[F] X Pr[P|F] =. 1 X. 2 =. 002

The General Multiplication Law Pr[A and B] = Pr[A] X Pr[B|A] And Pr[A and B] = Pr[B] X Pr[A|B] Notice that the probability for the first event in the product is an unconditional one, whereas the second is a conditional probability for the other event, given the first.

PROBABILITY TREES • Probability trees are useful to – calculate probabilities – identify all simple events – visualize the relationship among the events • Probability trees are useful if it is possible to – break down simple events into stages – identify mutually exclusive and exhaustive events at each stage – ascertain the probabilities of events at each stage

PROBABILITY TREES • A probability tree consists of some nodes and branches • Nodes – an initial unlabelled node called origin – other nodes, each labeled with the event represented by the node

PROBABILITY TREES • Branches – each branch connect a pair of nodes. – a branch from A to B implies that event B may occur after event A – each branch from • origin to A is labeled with probability P(A) • A to B is labeled with the probability P(B|A)

PROBABILITY TREES • Any path through the tree from the origin to a terminal node corresponds to one possible simple event. • All simple events and their probabilities are shown next to the terminal nodes.

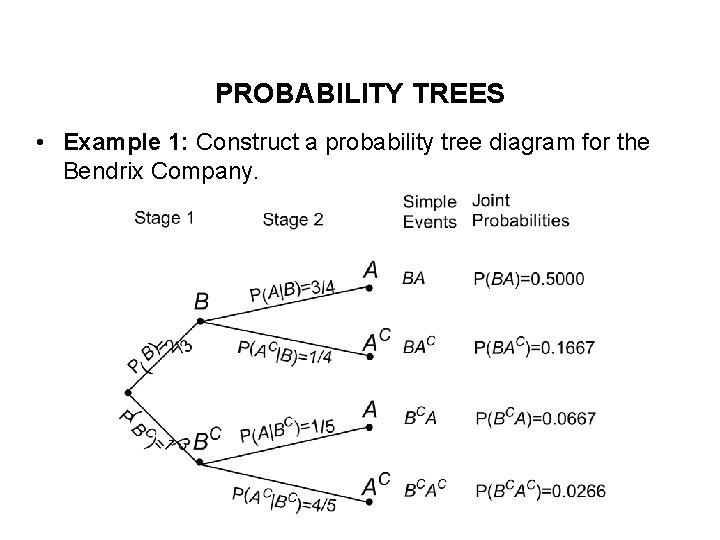
BENDRIX COMPANY’S SITUATION • The Bendrix Company supplies contractors with materials for the construction of houses. • Bendrix currently has a contract with one of its customers to fill an order by the end of July. • There is uncertainty about whether this deadline can be met, due to uncertainty about whether Bendrix will receive the materials it needs from one of its suppliers by the middle of July. It is currently July 1. • How can the uncertainty in this situation be assessed?

PROBABILITY TREES • Example 1: Construct a probability tree diagram for the Bendrix Company.

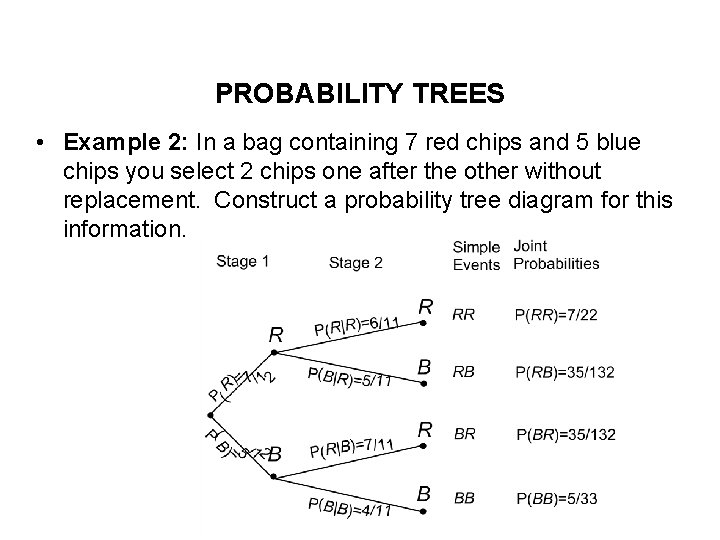
PROBABILITY TREES • Example 2: In a bag containing 7 red chips and 5 blue chips you select 2 chips one after the other without replacement. Construct a probability tree diagram for this information.

PROBABILITY TREES • What is the probability of getting a red chip first and then a blue chip? • What is the probability of getting a blue chip first and then a red chip? • What is the probability of getting a red and a blue chip? • What is the probability of getting 2 red chips?

Conditional Probability The four attendants of a gasoline service station are supposed to wash the windshield of each customer’s car. Janet, who services 20% of all cars, fails to wash the windshield one time in 20 Tom, who services 60% of all cars, fails to wash the windshield one time in 10 Georgia, who services 15% of all cars, fails to wash the windshield one time in 10 Peter, who services 5% of all cars, fails to wash the windshield one time in 20.

Conditional Probability If a customer later complained that her windshield was not washed, what is the probability that her car was serviced by Janet?

Solution All these are mutually exclusive events. Pr[windshield was not washed|Janet serviced the car] =