Spis treci Wprowadzenie Logarytmy Makrokosmos Mikrokosmos Spirala logarytmiczna

Spis treści Wprowadzenie Logarytmy Makrokosmos Mikrokosmos Spirala logarytmiczna Ciąg Fibonacciego Galaktyki Ziemia- natura Co z tego wynika?

Logarytmy Nasza przygoda z logarytmami zaczęła się na pewnej lekcji matematyki. Twoja może dopiero się rozpoczyna, albo ją dalej kontynuujesz. A więc logarytmem o podstawie a z liczby b nazywamy taką liczbę c, że a podniesione do potęgi c jest równe b, tzn. : log a b=c wtedy i tylko wtedy, gdy a c =b

Makrokosmos Fizyka gwiazd, czyli ich jasność Do okreslenia janosci gwiazd okazala się pomocna skala logarytmiczna. Obserwowaną(widomą) wielkość gwiazdowa, m(jasność obserwowana); mierzona w magnitudo(mag) określamy zależnością: m= -2, 5 log E Różnica wielkości gwiazdowych Obiektów jest wyrażona wzorem pagsona: m 1 -m 2=-2, 5 log(E 1/E 2)

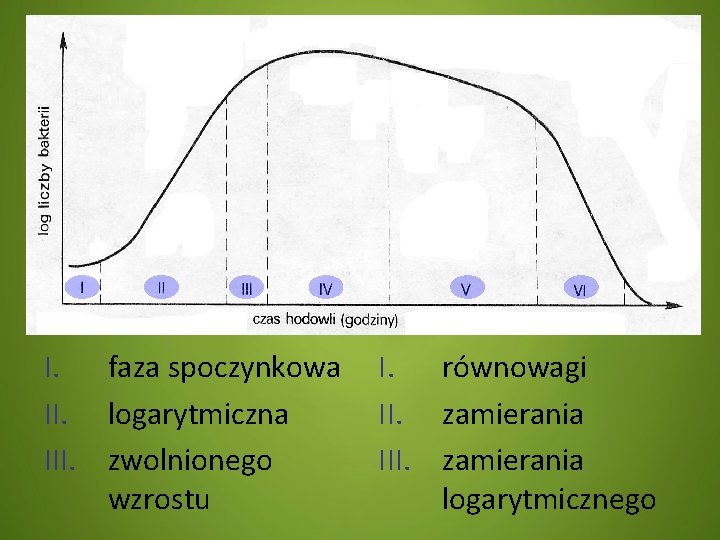
Mikrokosmos Zjawisko wzrostu drobnoustrojów można zobrazować za pomocą krzywej wzrostu bakterii. Na wykresie wyróżniono sześć faz rozwoju populacji. . .

I. faza spoczynkowa II. logarytmiczna III. zwolnionego wzrostu I. równowagi II. zamierania III. zamierania logarytmicznego

W fazie logarytmicznej dochodzi do intensywnych podziałów komórkowych, przez co liczba komórek rośnie w tempie geometrycznym, gdzie logarytm ilości bakterii jest wprost proporcjonalny do czasu. Wzrost w fazie log. opisuje wzór: N= N 0 * 2 n ,

wzór określający swoistą szybkość przyrostu masy organizmów bakteryjnych w jednostce czasu i jednostkę masy już istniejącej: M. = (ln x 2 -ln x 1) / (t 2 -t 1) , W fazie VI podziały komórek prawie całkowicie ustają. W rezultacie liczba komórek stale maleje. W niekorzystnych warunkach zamieranie może zachodzić bardzo szybko. Mówimy wtedy o fazie śmierci logarytmicznej.

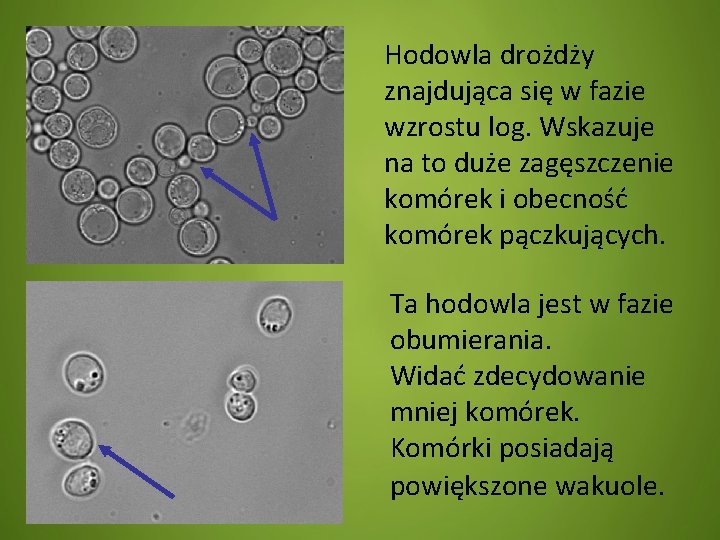
Hodowla drożdży znajdująca się w fazie wzrostu log. Wskazuje na to duże zagęszczenie komórek i obecność komórek pączkujących. Ta hodowla jest w fazie obumierania. Widać zdecydowanie mniej komórek. Komórki posiadają powiększone wakuole.

Ciąg Fibonacciego to ciąg liczb, który rozpoczyna się od 0 i 1, a każdy kolejny wyraz ciągu jest sumą dwóch poprzednich. Jest to jeden z najważniejszych ciągów, o wszechstronnym zastosowaniu, nie tylko w matematyce. Ciąg został podany przez Leonarda z Pizy zwanego Fibonaccim w swoim dziele Liber abaci (1202) Było to rozwiązanie zadania o rozmnażaniu się królików.

1 Króliki Fibonacciego 1 W kwadratach podano liczbę par na danym „poziomie”. 2 3 5

Innym przykładem obecności ciągu Fibonacciego w przyrodzie jest przyrost pędów roślinnych. Zatem wzór na zapis ciągu Fibonacciego wygląda:

Spirala logarytmiczna Spirala Logarytmiczna zwana też spiralą Fibonnaciego oraz złotą spiralą. Złoty podział, oparty jest liczbach, których suma dwóch poprzednich daje następną, tak na przykład: jeżeli I liczbą ciągu jest liczba 1, tak samo jak II jest również 1, 1+1=2 następną liczbą ciągu jest 2. Idąc dalej tym tokiem myślenia 1+2=3 i tak dalej - 2+3=5, 3+5=8 i tak w nieskończoność.

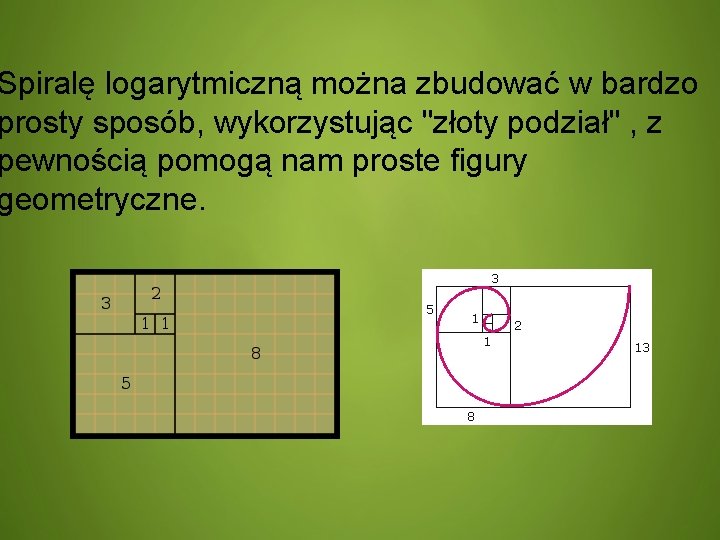
Spiralę logarytmiczną można zbudować w bardzo prosty sposób, wykorzystując "złoty podział" , z pewnością pomogą nam proste figury geometryczne.

Budowa galaktykspirala logarytmiczna Galaktyki, łącznie stanowią 4, 5% masy całego Wszechświata. Każda z galaktyk spiralnych posiada jądro otoczone dyskiem. Droga Mleczna jest jedną z galaktyk spiralnych.

Rodzaje galaktyk: 1. Eliptyczna 2. Soczewkowata 3. Nieregularne 4. Spiralne

Ciąg Fibonacciego w naturze W przyrodzie istnieja dużo bardziej racjonalne przypadki ciągu niż twierdzenie o królikach. Dowodem tego moga być np. : Układ pestek w tarczy słonecznika, lub uklad łusek w szysce.

Co z tego wynika? W trakcie naszej prezentacji miałeś okazję przekonać się, iż logarytmy otaczają cały twój świat. Nurtuje nas jedno pytanie: czy tak cudowny świat można opisać za pomocą zjawiska, jakimi są logarytmy? Na to pytanie niestety nikt nie jest w stanie odpowiedzieć.

Literatura: Bibliografia Astronomia, Państwowe zakłady wydawnictw szkolnych, Warszawa 1973 J. Nicklin, K. Graeme- Cook, R. Killington, Mikrobiologia - Krótkie wykłady wyd. II popr. i unow. , PWN, Warszawa 2004 E. Solomon, L. Berg, D. Martin, C. A. Villee, Biologia, wyd. II popr. , (wg III wyd. amer. ) MULTICO Oficyna Wydawnicza, Warszawa 2000 T. Szymczyk, S. Rabiej, A. Pielesz, J. Desselberger, Tablice matematyczne, fizyczne, chemiczne, astronomiczne James Trefil, 1001 Spotkań z nauką, wyd. Świat Książki, Warszawa 1997 Matematyka Fizyka Chemia, Wydawnictwo Naukowe PWN, Warszawa 2004 F. Sherman, Getting started with yeast M. Prescott, Microbiology, 5 th edition (2002) Zdjęcia mikroskopowe drożdży pochodzą z materiałów ćwiczeniowych z przedmiotu pracownia inżynierii genetycznej na Międzyuczelnianym Wydziale Biotechnologii UG i GUMed Strony internetowe: http: //vesta. astro. amu. edu. pl/Staff/Tkastr/Astro/geo-lec/node 103. html http: //vesta. astro. amu. edu. pl/Staff/Tkastr/Astro/geo-lec/node 102. html http: //news. astronet. pl/3012 http: //gwiazdozbiory. eulersoft. com. pl/dod_Jasnosci. Gwiazd. html http: //scientist. pl/viewtopic. php? t=1774