Mierniki efektywnoci inwestycji finansowych stopa zwrotu okresowa stopa

Mierniki efektywności inwestycji finansowych stopa zwrotu, okresowa stopa zwrotu z inwestycji wieloetapowej średnia geometryczna stopa zwrotu średnia arytmetyczna stopa zwrotu efektywna stopa zwrotu realna stopa zwrotu NPV- wartość bieżąca netto (net present value) IRR- wewnętrzna stopa zwrotu (internal rate of return) ERR- zewnętrzna stopa zwrotu (external rate of return) Stopy zwrotu w funduszach inwestycyjnych

Stopa zwrotu z inwestycji (1) R = (K - K 0) / K 0 gdzie K 0 – kapitał początkowy, K - kapitał końcowy

Inwestycje wieloetapowe Ciąg rocznych inwestycji zamkniętych

Inwestycje wieloetapowe Ciąg rocznych inwestycji zamkniętych Dowód. Rzeczywiście n K 1 = K 0 (1+ r 1) n K 2 = K 1 (1+ r 2) = K 0 (1+ r 1) (1+ r 2) n K 3 = K 2 (1+ r 3) = K 0 (1+ r 1) (1+ r 2) (1+ r 3). . . . . n Kn = Kn-1 (1+ rn) = K 0 (1+ r 1) (1+ r 2) (1+ r 3)… (1+ rn) Stąd i z uwagi 1 otrzymujemy (2). Aby średnia roczna stopa zwrotu rs generowała stopę zwrotu R z całej inwestycji, musi zachodzić równość (4) (1+ rs)n = Πni=1(1+ ri) , stąd otrzymujemy (3). Wzór ten można przedstawić w postaci (5) rs = ( R + 1)1/n – 1, czyli

Inwestycje wieloetapowe Ciąg rocznych inwestycji zamkniętych Zatem mamy (6) rs = ( R + 1)1/n – 1, czyli Wzór można interpretować jako wzór na średnią okresową stopę zwrotu z inwestycji trwającej n okresów bazowych i posiadającej stopę zwrotu R z całej inwestycji rs nosi nazwę średniej geometrycznej stopy zwrotu w okresie bazowym

Inwestycje wieloetapowe Ciąg inwestycji zamkniętych o etapach różnej długości n UWAGA 1. Jeśli kolejne inwestycje zamknięte o stopach zwrotu r 1, r 2, …, rn nie są związane z rocznymi okresami (każdy etap może mieć różną długość) to R we wzorze (2) pozostaje stopą zwrotu z ciągu inwestycji, zaś rs ze wzoru (3) jest średnią geometryczną stopą zwrotu w jednym etapie.

Inwestycje wieloetapowe Ciąg inwestycji kompensowanych Def. 3. Ciąg inwestycji nazywamy ciągiem inwestycji kompensowanych, jeżeli kolejna inwestycja ma taki sam kapitał początkowy jak poprzednia (kapitał jest uzupełniany w przypadku straty, odprowadzany - w przypadku zysku). n Twierdzenie 2. Niech dany będzie ciąg rocznych inwestycji kompensowanych, o stopach zwrotu odpowiednio: r 1, r 2, r 3, . . . , rn. Wtedy stopa zwrotu R całego ciągu inwestycji wynosi (7) R = ∑ni=1 ri zaś średnia roczna stopa zwrotu rsa wynosi (8)

Inwestycje wieloetapowe Ciąg inwestycji kompensowanych Dowód. Niech K 0 oznacza kapitał początkowy. Po roku dysponujemy kapitałem K 1 = K 0 (1+ r 1) , odprowadzamy K 0 r 1. Po drugiej inwestycji - kapitałem K 2 = K 0 (1+ r 2) , odprowadzamy K 0 r 2, i. t. d. Po n-tej inwestycji mamy Kn = K 0 (1+ rn) , odprowadzamy K 0 rn, pozostało K 0. Kapitał końcowy to suma K 0 oraz wszystkich odprowadzonych kwot, początkowy to K 0. R = [( K 0+ K 0 r 1+ K 0 r 2+. . . + K 0 rn ) – K 0 ]/ K 0. Stąd R = r 1 + r 2 +. . . + rn Ponieważ stopa zysku jest sumą stóp z poszczególnych inwestycji, więc średnia roczna stopa zwrotu musi czynić zadość równości: rsa+ rsa +. . . + rsa= n rsa= R czyli rsa = R/n lub inaczej

Inwestycje wieloetapowe Ciąg inwestycji kompensowanych o etapach różnej długości n UWAGA 2. Jeśli kolejne inwestycje kompensowane o stopach zwrotu r 1, r 2, …, rn nie są związane z rocznymi okresami (każdy etap może mieć różną długość) to R we wzorze (7) pozostaje stopą zwrotu z ciągu inwestycji, zaś rsa ze wzoru (8) jest średnią arytmetyczną stopą zwrotu w jednym etapie.

Porównanie średniej arytmetycznej i średniej geometrycznej stopy zwrotu

Porównanie stóp zwrotu z ciągu inwestycji wieloetapowych o dodatnich stopach zwrotu

Inwestycje wieloetapowe Ciągi inwestycji o etapach różnej długości n UWAGA 3. Twierdzenia 3 i 4 pozostają prawdziwe, gdy r 1, r 2, …, rn są stopami dotyczącymi dowolnych przedziałów czasowych

Efektywna roczna stopa zwrotu n Niech r oznacza nominalną roczną stopę zwrotu oferowaną przez bank, w którym w ciągu roku dokonuje się n – kapitalizacji. Wtedy efektywna roczna stopa zwrotu wynosi

Realna roczna stopa zwrotu Def. 6. Realną roczną stopą zwrotu nazywamy liczbę mierzącą względny przyrost wartości nabywczej pieniądza w okresie jednego roku. n Niech K oznacza początkowy koszt standardowego koszyka dóbr, f – roczną stopę inflacji, re - efektywną roczną stopę zwrotu zaś rr - realną roczną stopą zwrotu. Koszt koszyka po roku wynosi K(1+f). n Kwota K po rocznej inwestycji wzrosła do K(1+ re). Zatem po roku można nabyć K(1+ re)/ K(1+f) standardowych koszyków. Ponieważ przed rokiem mogliśmy nabyć 1 koszyk więc przyrost wartości nabywczej rr wynosi (9)

Realna roczna stopa zwrotu Po dodaniu 1 do obu stron równania otrzymujemy tzw. wzór Fischera: (10)

Stopa zwrotu ponad zysk wolny od ryzyka Przykład. Niech roczna stopa zysku wolnego od ryzyka wynosi 8%. Inwestor giełdowy osiągnął w ciągu roku zysk 12 %. O ile procent więcej zarobił inwestor giełdowy od inwestora nie podejmującego ryzyka ? Zakładając kwotę początkową K dla obu inwestycji, odpowiedź na pytanie daje liczba Jest to sytuacja analogiczna do tej, przy stopie realnej (porównanie z wzorem (10)). Przy oznaczeniach: r - stopa zwrotu z inwestycji, rw- stopa zysku wolnego od ryzyka otrzymujemy wzór na stopę zwrotu r* ponad zysk wolny od ryzyka (11)

Logarytmiczna stopa zwrotu z inwestycji o dwóch przepływach: nakładzie i przychodzie Nakład - K 0, Przychód – K 1 Def. Logarytmiczną stopą zwrotu z inwestycji o przepływach K 0, K 1 nazywamy wyrażenie (12) r = ln(K 1 /K 0) Dla ciągu inwestycji zamkniętych logarytmiczna stopa zwrotu R z całej inwestycji jest sumą logarytmicznych stóp zwrotu z poszczególnych etapów. Mamy bowiem: R = ln (Kn/K 0) = ln(K 1/K 0 K 2/K 1 … Kn/Kn-1 ) = = ln(K 1/K 0)+ln(K 2/K 1)+… +ln(Kn/Kn-1) =r 1+ r 2 +…+ rn Zatem średnia logarytmiczna stopa zwrotu z jednego etapu jest równa średniej arytmetycznej z logarytmicznych stóp zwrotu z poszczególnych etapów

Wartość bieżąca netto (NPV) net present value Inwestycję finansową traktujemy jako ciąg nakładów i dochodów (przepływów finansowych), znanych co do wielkości i momentów wystąpienia. n Def. Wartość bieżąca netto inwestycji to suma zdyskontowanych przepływów netto (dochód minus nakład z tej samej chwili) z inwestycji przy ustalonej stopie procentowej. n Przy założeniu kapitalizacji okresowej, wartość tego wskaźnika obliczamy ze wzoru : (13)

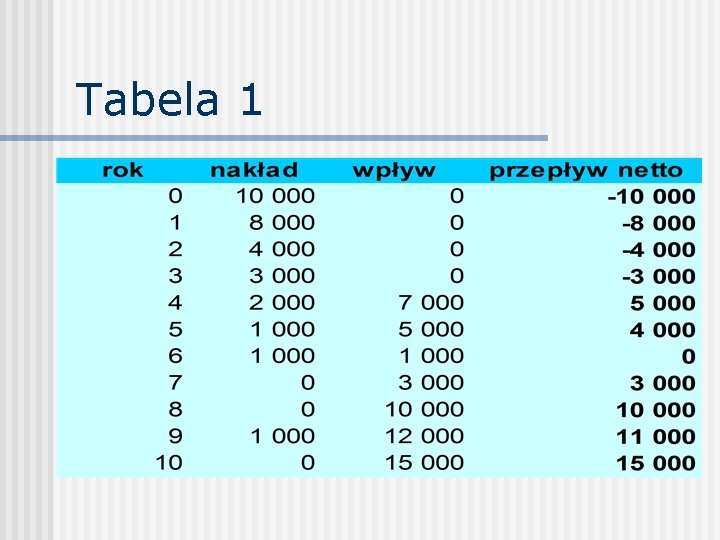
Tabela 1

Wartość bieżąca netto Ci - i-ty przepływ finansowy netto, ti – czas od przepływu zerowego do i - tego, mierzony liczbą okresów bazowych, (zatem t 0=0), r – stopa procentowa w okresie bazowym. Okres bazowy może być rokiem, kwartałem, miesiącem, itp. Dodatnie Ci oznaczają dochód netto, ujemne – nakład netto. Kolejność wydatków i dochodów jest dowolna. Na ogół przepływ C 0 jest ujemny (wydatek).

Wartość bieżąca netto / szczególny przypadek Przy jednym nakładzie dokonanym na początku wzór przyjmuje postać (14) Gdzie dodatnie I oznacza wielkość początkowego nakładu, Ci są także dodatnie.

NPV – szczególny przypadek modyfikacja

Wartość bieżąca netto n Uwaga 4. Jeżeli wartość wskaźnika NPV jest dodatnia oznacza to, że inwestycja jest opłacalna. Przy ujemnej wartości tego wskaźnika inwestycję uważamy za nieopłacalną. n Uwaga 5. Jeżeli dane są dwie inwestycje o tym samym NPV, to korzystniejsza jest ta, która angażuje mniejszy kapitał.

Wartość bieżąca netto (NPV) n n Przykład 1. Czy warto zainwestować 1500 $ w przedsięwzięcie, które przyniesie za rok 100 $, po dwóch latach 200 $, po trzech 300 $, po czterech 400 $ i po pięciu 500 $, jeżeli roczna stopa procentowa wolna od ryzyka wynosi w tym okresie 6 % ? Korzystając ze wzoru (42) otrzymujemy Oceniając inwestycję na podstawie NPV, stwierdzamy, że jest ona nieopłacalna.

Wartość bieżąca netto (NPV) / interpretacja Z wyżej otrzymanej równości mamy także Interpretacja równości (w aspekcie zasady równoważności długu i spłat) Kwota 1214, 69 $ powinna wygenerować dany ciąg wpływów przy rocznej stopie w wys. 6 %. Może być interpretowana jako kwota kredytu, która przynosi bankierowi od dłużnika wymienione dochody w odpowiednich chwilach (pożyczka udzielona przez bankiera jest dla niego inwestycją). Inwestując 1500 $ by uzyskać wymienione wyżej przypływy „przepłacamy” więc aż 285, 31 $.

Wartość bieżąca netto (NPV) Wniosek. Jeżeli NPV = 0, to inwestycja jest tak samo opłacalna jak lokata bankowa o oprocentowaniu rocznym równym stopie dyskontowej użytej do obliczenia NPV, przy rocznej kapitalizacji odsetek. Jeżeli NPV > 0, to inwestycja jest bardziej opłacalna niż lokata bankowa przy stopie r, jeżeli natomiast NPV < 0, to jest mniej opłacalna.

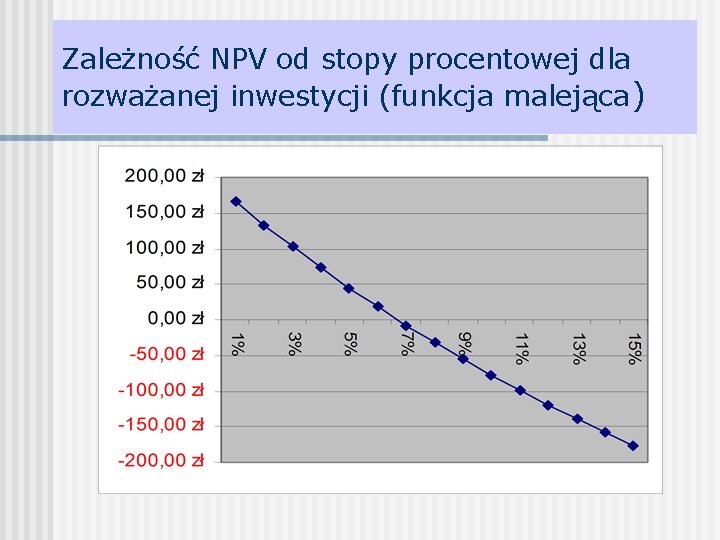
Zależność wskaźnika NPV od stopy dyskontowej Przykład. Inwestycja 800 zł przynosi po roku wpływ w wysokości 100 zł a w następnych latach odpowiednio: 150, 200, 250, 300 zł. Oblicz NPV tej inwestycji przy różnych stopach procentowych ( od 1% do 15 % ).

Zależność NPV od stopy procentowej dla rozważanej inwestycji (funkcja malejąca)

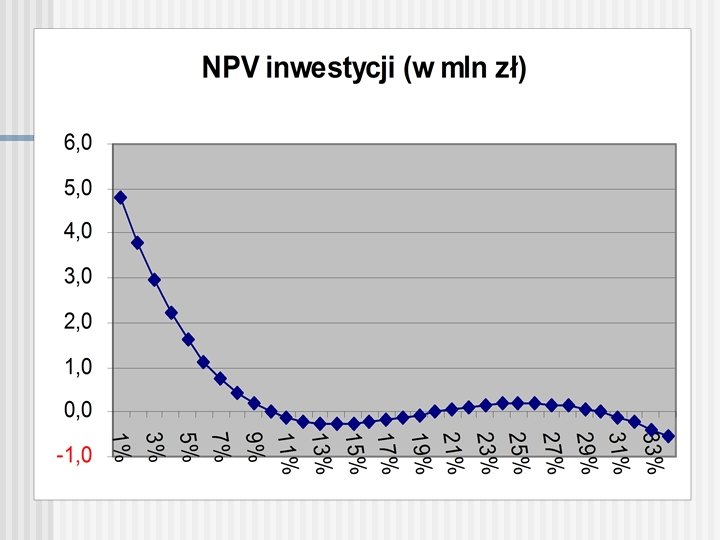
Zależność wskaźnika NPV od stopy procentowej dla inwestycji o dużych przepływach różnych znaków Przykład 2. Inwestycja w wysokości 1 mln zł przynosi po roku wpływ w wysokości 3, 6 mln zł w następnym roku stratę 4, 31 mln a rok później zysk 1, 716 mln zł. Zbadamy zależność wskaźnika NPV od stopy procentowej

Wartość bieżąca netto (NPV) podsumowanie Zalety wskaźnika n łatwość w obliczeniu n jednoznaczność (przy ustalonej stopie dyskontowej) n mianowanie w użytych w przepływach jednostkach monetarnych Wady n zależność od skali inwestycji (pomnożenie nakładów i dochodów przez liczbę skutkuje zmianą NPV) n zależność od wyboru stopy dyskontowej (nietrafny wybór stopy może zmienić znak wskaźnika)

Indeks zyskowności PI Profitability index PI=NPV/I gdzie I – wielkość zainwestowanej kwoty n Standaryzacja NPV n PI – niewrażliwy na skalę inwestycji n

Wewnętrzna stopa zwrotu (IRR) internal rate of return n Def. Wewnętrzną stopą zwrotu ciągu przepływów finansowych C 0, C 1 , C 2 , . . . , Cn jest taka stopa procentowa, przy której wartość bieżąca netto tych przepływów jest równa zeru, czyli takie r, że (15) n Wzór (15) jest równaniem względem r, stopnia tn. Niektóre Ci są dodatnie, niektóre ujemne. Muszą wystąpić przepływy różnych znaków, n t 0=0

IRR - przypadek jedynego nakładu I dokonanego na początku, Ci dodatnie.

IRR - szczególny przypadek (modyfikacja), jedyny nakład I dokonany na początku, Ci nieujemne

Brak jednoznacznego rozwiązania równania (15) Inwestycja z przykładu 2. (nakład w wysokości 1 mln zł przynosi po roku wpływ w wysokości 3, 6 mln zł w następnym roku stratę 4, 31 mln a rok później zysk 1, 716 mln zł) nie posiada jednoznacznie wyznaczonej wewnętrznej stopy zwrotu. Wynika to z wykresu NPV dla tej inwestycji (3 miejsca zerowe wykresu)

Brak rozwiązania równania (15) w zbiorze liczb rzeczywistych Inwestycja 100$ przynosi po roku przychód 200$ zaś po dwóch latach stratę 101$. n Równanie definiujące IRR dla tej inwestycji -100 + 200/(1+r) – 101/(1+r)2 = 0 ma tylko pierwiastki zespolone n

Jednoznaczność rozwiązania równania korespondującego z równaniem definiującym IRR TW. Jeżeli strumień c 0 , c 1, . . . , cn , przepływów spełnia warunki: c 0 < 0, pozostałe przepływy są nieujemne, przynajmniej jeden jest dodatni, to istnieje jednoznaczne rozwiązanie równania c 0 + c 1 x + c 2 x 2+. . . + cnxn = 0

Jednoznaczność rozwiązania równania korespondującego z równaniem definiującym IRR Dowód: f(x) = c 0 + c 1 x + c 2 x 2+. . . + cnxn g(x)= c 1 x + c 2 x 2+. . . + cnxn Z założeń o ci wynika, że g jest rosnąca dla nieujemnych argumentów oraz g(x) > 0 dla x > 0 Funkcja f jest ciągła oraz f(0) < 0. Wykres f jest przesunięciem w dół wykresu funkcji rosnącej g, ma więc jeden punkt wspólny z osią OX, po jej dodatniej stronie.

Wewnętrzna stopa zwrotu / przykład n n n Przykład 1. Bank udzielił pożyczki w kwocie 800 zł. Dłużnik spłaci po roku 100 zł, po dwóch latach 120, po trzech 200 zł, po czterech 250 zł, po pięciu 300 zł. Jaka jest wewnętrzna stopa zwrotu tej inwestycji dla banku ? Szukana stopa jest rozwiązaniem równania Jest to równanie 5 – tego stopnia. Jedynym jego pierwiastkiem jest liczba 6, 69 % (z dokł. do setnej).

Wewnętrzna stopa zwrotu z inwestycji w obligację zerokuponową n n n Przykład 2. Zerokuponowa obligacja dziesięcioletnia o wartości nominalnej 100 zł jest sprzedawana po 60 zł. Jaką wewnętrzną stopę zwrotu ma inwestycja w tą obligację? Rozwiązaniem równania Stopa IRR jest w tym przypadku również średnią roczną stopą zwrotu z tej inwestycji (wzór (6))

Wewnętrzna stopa zwrotu z inwestycji w obligację kuponową n n n Przykład 3. Obligacja kuponowa o cenie sprzedaży 1000 zł generuje 11 co miesięcznych wypłat po 20 zł oraz dwunastą w wys. 1020 zł. Jaka jest wewnętrzna stopa zwrotu z tej inwestycji w ujęciu miesięcznym? Należy rozwiązać równanie 12 – tego stopnia Okazuje się, że r = 2% jest jego rozwiązaniem. Jest to tzw. stopa rentowności obligacji

IRR - uwagi 1. Z dwóch inwestycji lepsza jest ta, która ma wyższy IRR n 2. Równanie (15) może mieć kilka rozwiązań. ( Dany jest przepływ kapitałów: - 1000 $, +3600 $ , - 4310 $, + 1716 $ w rocznych odstępach czasowych. Liczby 10%, 20 %, 30 % spełniają równanie (15) dla tego przepływu kapitału). n 3. Jeżeli występuje tylko początkowy nakład, to IRR jest wyznaczona jednoznacznie. n 4. Inwestycja jest opłacalna, jeżeli jej IRR przewyższa stopę procentową wolną od ryzyka (np. oprocentowania lokat bankowych), jeżeli zaś jest od niej mniejsza, to inwestycja jest nieopłacalna. n

IRR - podsumowanie Zalety n brak wrażliwości na skalę inwestycji n porównywalność z innymi miernikami efektywności inwestycji (stopa efektywna, stopa rentowności obligacji) n pełnienie roli okresowej efektywnej stopy zwrotu Wady n wskaźnik IRR (w wielu przypadkach) możliwy do obliczenia tylko metodami numerycznymi n niejednoznaczność (równanie (15) może posiadać więcej niż jedno rozwiązanie)

Profitability index PI n Współczynnik PI można zdefiniować także w przypadku gdy nakłady rozciągnięte są w czasie n Primowane Ci oznaczają wpływy, Ii nakłady (zob. Tabela 1) Można zauważyć, że PI=1 tylko wtedy gdy stopa procentowa użyta do dyskontowania r = IRR n

Stopa zwrotu z inwestycji o wielu przychodach bez reinwestycji Niech inwestycja I przynosi w kolejnych latach przypływy finansowe c 1 , . . . , cn. Stopa zwrotu R z inwestycji dana jest wzorem

Średnia okresowa stopa zwrotu rs gdy ostatni przepływ nastąpił po tn okresach

Reinwestowanie wpływów przy stałej stopie procentowej r Uzyskane w czasie trwania inwestycji wpływy inwestujemy bezzwłocznie uzyskując stałą okresową stopę zwrotu r Obliczymy stopę zwrotu z inwestycji i średnią okresową stopę zwrotu przy reinwestowaniu wpływów

Reinwestowanie wpływów przy stopie r n Inwestując każdy wpływ przy stopie procentowej r, w momencie ostatniego wpływu otrzymujemy kwotę n Oznaczając – jak poprzednio- stopę zwrotu z całej inwestycji przez R otrzymujemy

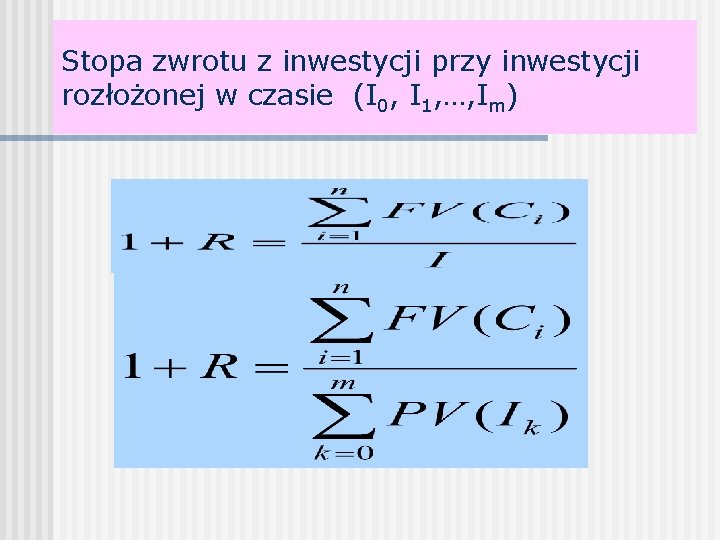
Stopa zwrotu z inwestycji przy inwestycji rozłożonej w czasie (I 0, I 1, …, Im)

Zewnętrzna stopa zwrotu ERR n Inwestycja trwa tn lat zatem średnia roczna stopa zwrotu rs spełnia równanie (rs nosi nazwę zewnętrznej stopy zwrotu)

ERR (external rate of return)

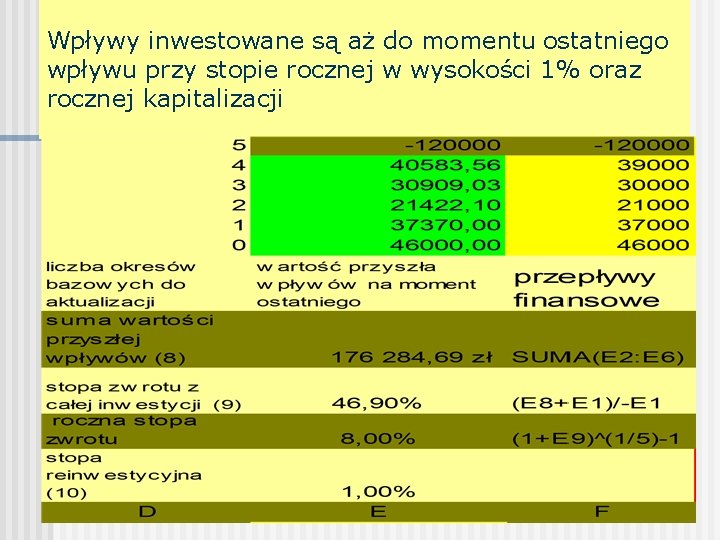
Stopa zwrotu z inwestycji i średnia okresowa stopa zwrotu przy reinwestowaniu wpływów (modyfikacja) (powrót) Stopa zwrotu Średnia okresowa stopa zwrotu - rs (ERR)

Wpływy inwestowane są aż do momentu ostatniego wpływu przy stopie rocznej w wysokości 1% oraz rocznej kapitalizacji

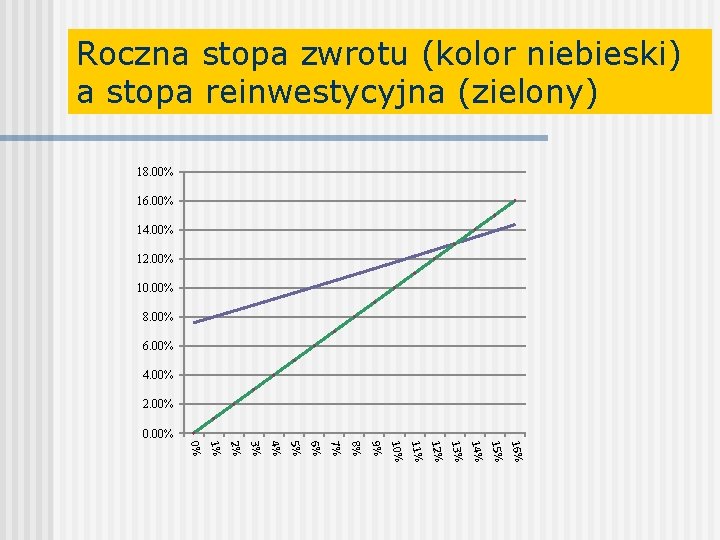
Roczna stopa zwrotu (kolor niebieski) a stopa reinwestycyjna (zielony) 18. 00% 16. 00% 14. 00% 12. 00% 10. 00% 8. 00% 6. 00% 4. 00% 2. 00% 0. 00% 16% 15% 14% 13% 12% 11% 10% 9% 8% 7% 6% 5% 4% 3% 2% 1% 0%

Uwaga n n n Dla pewnej wartości stopy reinwestycyjnej występuje równość z okresową stopą zwrotu z inwestycji (rs lub inaczej ERR) Okazuje się, że taka wartość stopy reinwestycyjnej jest równa wewnętrznej stopie zwrotu (IRR) Jeśli nie jest możliwe reinwestowanie przy stopie IRR, to ERR oznaczająca „rzeczywistą” stopę uzyskana z inwestycji jest mniejsza od IRR. Zatem IRR pozostaje „teoretyczną” stopą zwrotu.

Reinwestowanie wpływów przy stopie r =IRR (wtedy ERR = IRR)

Zrealizowana składana stopa zwrotu Realized compound rate - RCY (modyfikacja ERR) n Zakładamy, że nastąpiła inwestycja I w chwili t 0=0, pierwszy wpływ C 1 w t 1 =1, itd. . Cn w chwili tn oraz że w każdym rocznym okresie obowiązuje inna stopa reinwestycji ( w okresie (ti-1, ti) stopa ri. Poniższe wzory definiują stopę RCY, która jest modyfikacją ERR

Stopa zwrotu ważona kwotowo i, funduszu inwestycyjnego o wartości początkowej A, końcowej (po roku) B, wpływach C 1, …, Cm w chwilach t 1, …, tm z przedziału (0; 1)

Stopa zwrotu ważona czasowo r, funduszu inwestycyjnego o wartości początkowej A 0, końcowej (po roku) B, wpływach C 1, …, Cm w chwilach t 1, …, tm z przedziału (0; 1) i wartościach funduszu A 1, …, Am tuż przed kolejnymi wpłatami C 1, …, Cm. (jeśli następuje wypłata, to C jest ujemne)

Przykład. Fundusz w pierwszym półroczu uzyskał 50% stratę, w drugim 100% wzrost. A) Oblicz stopę zwrotu ważoną czasowo. B) Oblicz stopę zwrotu ważoną kwotowo dla A=100, C 1=50. C) Oblicz stopę zwrotu ważoną kwotowo dla A=100, C 1=-40. D) Oblicz stopę zwrotu ważoną kwotowo dla A=100, C 1=0.

Przykład n 01. stycznia pewien fundusz miał wartość 100 tys. $. Dnia 01. 05. wartość funduszu wzrosła do 112 tys. oraz nastąpiła wpłata 30 tys. $. Dnia 01. 11. wartość funduszu wyniosła 125 tys. $ i nastąpiła wypłata 42 tys. $. Dnia 01. fundusz był znowu wart 100 tys. $. Jaka była stopa zwrotu ważona czasowo ?

Okres zwrotu inwestycji – długość takiego okresu [0; T], w którym wartość NPV wynosi zero W drugim przypadku dokładniejsze określenie okresu zwrotu T wymaga zastosowania metod aproksymacyjnych

Okres zwrotu inwestycji - własności n n n Zależy od wyboru stopy procentowej r Może nie istnieć (przy małych przychodach) Gdy nakłady przeplatają się z dochodami – nie jest wyznaczony jednoznacznie, gdyż można wtedy wskazać kilka okresów zwrotu związanych z kolejnymi cyklami nakładów i przychodów Nie zależy od skali inwestycji Jeśli istnieje IRR, to przy stopie r=IRR okres zwrotu pokrywa się z okresem inwestycji, (gdy r>IRR to OZ nie istnieje; gdy r<IRR, to OZ krótszy od okresu inwestycji) Nie istnieje, jeśli inwestycja ma tylko jeden początkowy nakład oraz jej NPV<0, (NPV liczone przy tym samym r)

Roczna wewnętrzna stopa zwrotu r inwestycji o jednym nakładzie (PV) w rentę wieczystą, wypłacającą jednakowe roczne kwoty (W). n Stopę r zdefiniujemy jako granicę ciągu wewnętrznych stóp zwrotu rn dla skończonego ciągu n jednakowych wypłat: