Sparse Recovery Using Sparse Matrices Piotr Indyk MIT

Sparse Recovery (Using Sparse Matrices) Piotr Indyk MIT

Heavy Hitters • Also called frequent elements and elephants • Define HHpφ (x) = { i: |xi| ≥ φ ||x||p } • Lp Heavy Hitter Problem: – Parameters: φ and φ’ (often φ’ = φ-ε) – Goal: return a set S of coordinates s. t. • S contains HHpφ (x) • S is included in HHpφ’ (x) • Lp Point Query Problem: – Parameter: – Goal: at the end of the stream, given i, report x*i=xi ||x||p Can solve L 2 point query problem, with parameter and failure probability P by storing O(1/ 2 log(1/P)) numbers sketches [A-Gibbons-M-S’ 99], [Gilbert-Kotidis-Muthukrishnan-Strauss’ 01]

Sparse Recovery • (approximation theory, learning Fourier coeffs, linear sketching, finite rate of innovation, compressed sensing. . . ) Setup: – Data/signal in n-dimensional space : x E. g. , x is an 256 x 256 image n=65536 – Goal: compress x into a “sketch” Ax , where A is a m x n “sketch matrix”, m << n • Requirements: – Plan A: want to recover x from Ax • Impossible: underdetermined system of equations – Plan B: want to recover an “approximation” x* of x • Sparsity parameter k • Informally: want to recover largest k coordinates of x • Formally: want x* such that ||x*-x||p C(k) minx’ ||x’-x||q over all x’ that are k-sparse (at most k non-zero entries) • Want: – Good compression (small m=m(k, n)) – Efficient algorithms for encoding and recovery • Why linear compression ? A x = Ax

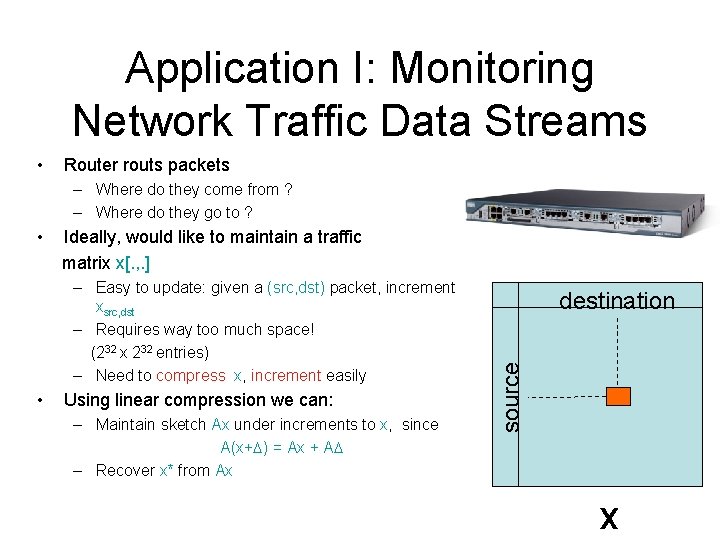
Application I: Monitoring Network Traffic Data Streams • Router routs packets – Where do they come from ? – Where do they go to ? Ideally, would like to maintain a traffic matrix x[. , . ] – Easy to update: given a (src, dst) packet, increment xsrc, dst – Requires way too much space! (232 x 232 entries) – Need to compress x, increment easily • Using linear compression we can: – Maintain sketch Ax under increments to x, since A(x+ ) = Ax + A – Recover x* from Ax destination source • x

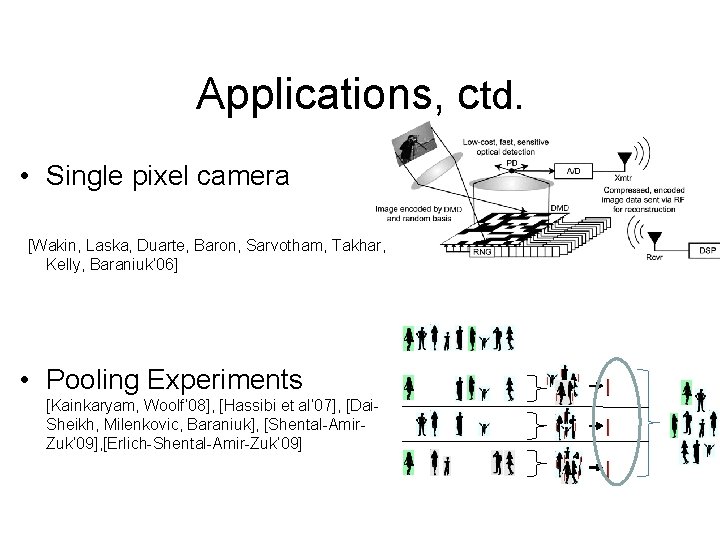
Applications, ctd. • Single pixel camera [Wakin, Laska, Duarte, Baron, Sarvotham, Takhar, Kelly, Baraniuk’ 06] • Pooling Experiments [Kainkaryam, Woolf’ 08], [Hassibi et al’ 07], [Dai. Sheikh, Milenkovic, Baraniuk], [Shental-Amir. Zuk’ 09], [Erlich-Shental-Amir-Zuk’ 09]

Constructing matrix A • “Most” matrices A work – Sparse matrices: • Data stream algorithms • Coding theory (LDPCs) – Dense matrices: • Compressed sensing • Complexity/learning theory (Fourier matrices) • “Traditional” tradeoffs: – Sparse: computationally more efficient, explicit – Dense: shorter sketches • Recent results: the “best of both worlds”

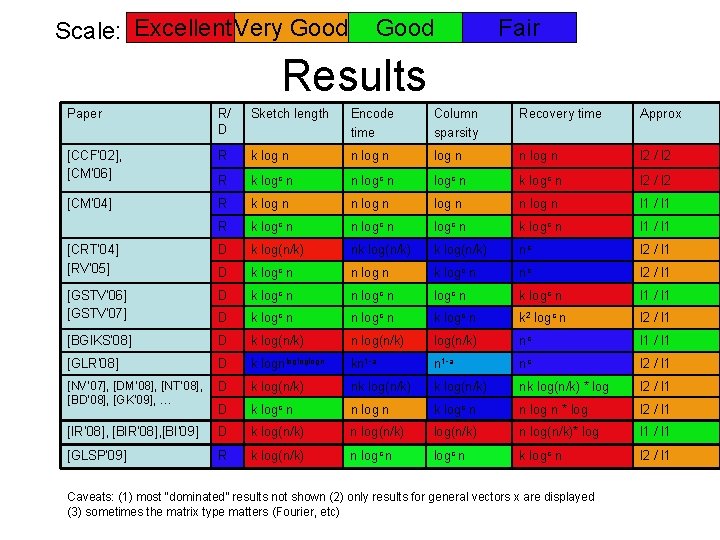
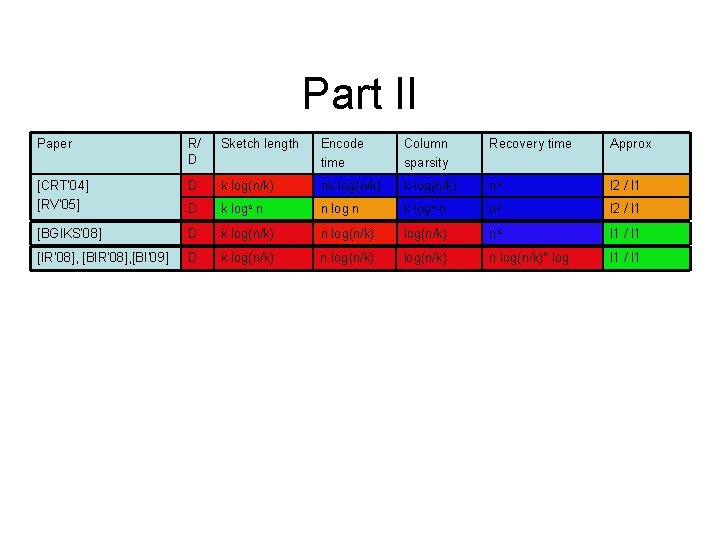
Scale: Excellent Very Good Fair Results Paper R/ D Sketch length Encode time Column sparsity Recovery time Approx [CCF’ 02], [CM’ 06] R k log n n log n l 2 / l 2 R k logc n n logc n k logc n l 2 / l 2 [CM’ 04] R k log n n log n l 1 / l 1 R k logc n n logc n k logc n l 1 / l 1 [CRT’ 04] [RV’ 05] D k log(n/k) nk log(n/k) nc l 2 / l 1 D k logc n n log n k logc n nc l 2 / l 1 [GSTV’ 06] [GSTV’ 07] D k logc n n logc n k logc n l 1 / l 1 D k logc n n logc n k 2 logc n l 2 / l 1 [BGIKS’ 08] D k log(n/k) nc l 1 / l 1 [GLR’ 08] D k lognlogloglogn kn 1 -a nc l 2 / l 1 [NV’ 07], [DM’ 08], [NT’ 08], [BD’ 08], [GK’ 09], … D k log(n/k) nk log(n/k) * log l 2 / l 1 D k logc n n log n * log l 2 / l 1 [IR’ 08], [BI’ 09] D k log(n/k) n log(n/k)* log l 1 / l 1 [GLSP’ 09] R k log(n/k) n logc n k logc n l 2 / l 1 Caveats: (1) most “dominated” results not shown (2) only results for general vectors x are displayed (3) sometimes the matrix type matters (Fourier, etc)

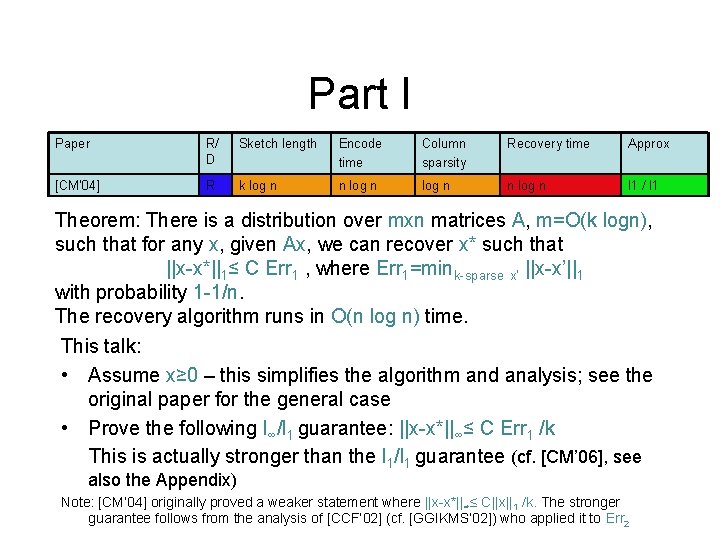
Part I Paper R/ D Sketch length Encode time Column sparsity Recovery time Approx [CM’ 04] R k log n n log n l 1 / l 1 Theorem: There is a distribution over mxn matrices A, m=O(k logn), such that for any x, given Ax, we can recover x* such that ||x-x*||1≤ C Err 1 , where Err 1=mink-sparse x’ ||x-x’||1 with probability 1 -1/n. The recovery algorithm runs in O(n log n) time. This talk: • Assume x≥ 0 – this simplifies the algorithm and analysis; see the original paper for the general case • Prove the following l∞/l 1 guarantee: ||x-x*||∞≤ C Err 1 /k This is actually stronger than the l 1/l 1 guarantee (cf. [CM’ 06], see also the Appendix) Note: [CM’ 04] originally proved a weaker statement where ||x-x*||∞≤ C||x||1 /k. The stronger guarantee follows from the analysis of [CCF’ 02] (cf. [GGIKMS’ 02]) who applied it to Err 2

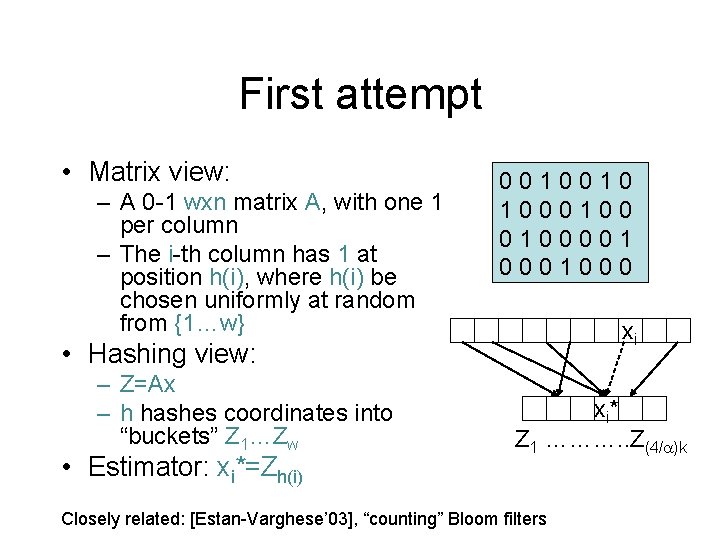
First attempt • Matrix view: – A 0 -1 wxn matrix A, with one 1 per column – The i-th column has 1 at position h(i), where h(i) be chosen uniformly at random from {1…w} 0010010 1000100001 0001000 xi • Hashing view: – Z=Ax – h hashes coordinates into “buckets” Z 1…Zw • Estimator: xi*=Zh(i) xi* Z 1 ………. . Z(4/ )k Closely related: [Estan-Varghese’ 03], “counting” Bloom filters

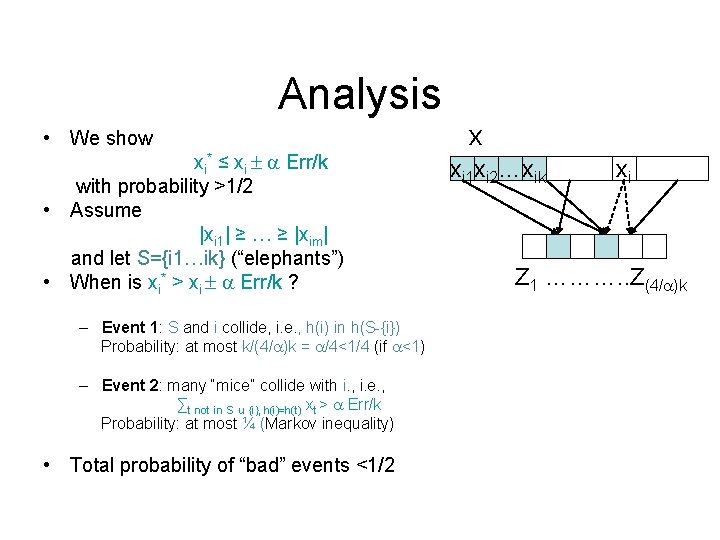
Analysis • We show xi* ≤ xi Err/k with probability >1/2 • Assume |xi 1| ≥ … ≥ |xim| and let S={i 1…ik} (“elephants”) • When is xi* > xi Err/k ? – Event 1: S and i collide, i. e. , h(i) in h(S-{i}) Probability: at most k/(4/ )k = /4<1/4 (if <1) – Event 2: many “mice” collide with i. , i. e. , ∑t not in S u {i}, h(i)=h(t) xt > Err/k Probability: at most ¼ (Markov inequality) • Total probability of “bad” events <1/2 x xi 1 xi 2…xik xi Z 1 ………. . Z(4/ )k

Second try • Algorithm: – Maintain d functions h 1…hd and vectors Z 1…Zd – Estimator: Xi*=mint Ztht(i) • Analysis: – Pr[|xi*-xi| ≥ α Err/k ] ≤ 1/2 d – Setting d=O(log n) (and thus m=O(k log n) ) ensures that w. h. p |x*i-xi|< α Err/k

Part II Paper R/ D Sketch length Encode time Column sparsity Recovery time Approx [CRT’ 04] [RV’ 05] D k log(n/k) nk log(n/k) nc l 2 / l 1 D k logc n n log n k logc n nc l 2 / l 1 [BGIKS’ 08] D k log(n/k) nc l 1 / l 1 [IR’ 08], [BI’ 09] D k log(n/k) n log(n/k)* log l 1 / l 1

Compressed Sensing • A. k. a. compressive sensing or compressive sampling [Candes-Romberg-Tao’ 04; Donoho’ 04] • Signal acquisition/processing framework: – Want to acquire a signal x=[x 1…xn] – Acquisition proceeds by computing Ax+noise of dimension m<<n • We ignore noise in this lecture – From Ax we want to recover an approximation x* of x • Note: x* does not have to be k-sparse in general – Method: solve the following program: minimize ||x*||1 subject to Ax*=Ax – Guarantee: for some C>1 (1) ||x-x*||1 ≤ C mink-sparse x” ||x-x”||1 (2) ||x-x*||2 ≤ C mink-sparse x” ||x-x”||1 /k 1/2

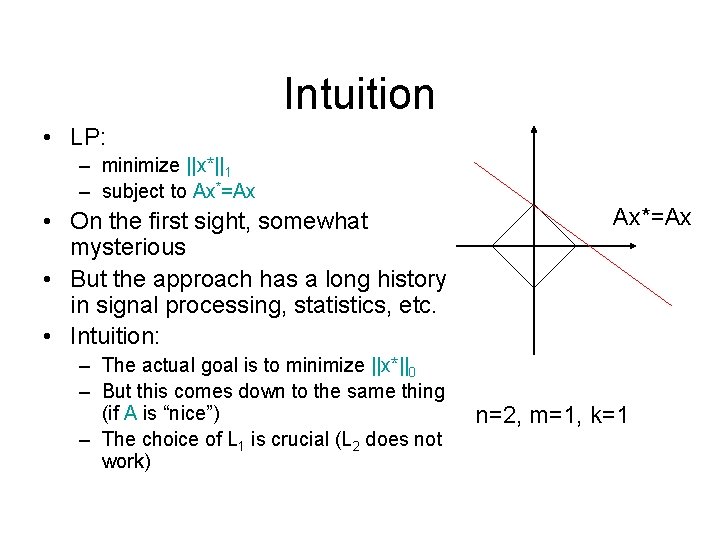
Linear Programming • Recovery: – minimize ||x*||1 – subject to Ax*=Ax • This is a linear program: – minimize ∑i ti – subject to • -ti ≤ x*i ≤ ti • Ax*=Ax • Can solve in nΘ(1) time

Intuition • LP: – minimize ||x*||1 – subject to Ax*=Ax • On the first sight, somewhat mysterious • But the approach has a long history in signal processing, statistics, etc. • Intuition: – The actual goal is to minimize ||x*||0 – But this comes down to the same thing (if A is “nice”) – The choice of L 1 is crucial (L 2 does not work) Ax*=Ax n=2, m=1, k=1

Restricted Isometry Property • A matrix A satisfies RIP of order k with constant δ if for any k-sparse vector x we have (1 -δ) ||x||2 ≤ ||Ax||2 ≤ (1+δ) ||x||2 • Theorem 1: If each entry of A is i. i. d. as N(0, 1), and m=Θ(k log(n/k)), then A satisfies (k, 1/3)-RIP w. h. p. • Theorem 2: (O(k), 1/3)-RIP implies L 2/L 1 guarantee [CRT’ 04] [RV’ 05] D k log(n/k) nk log(n/k) nc l 2 / l 1 D k logc n n log n k logc n nc l 2 / l 1

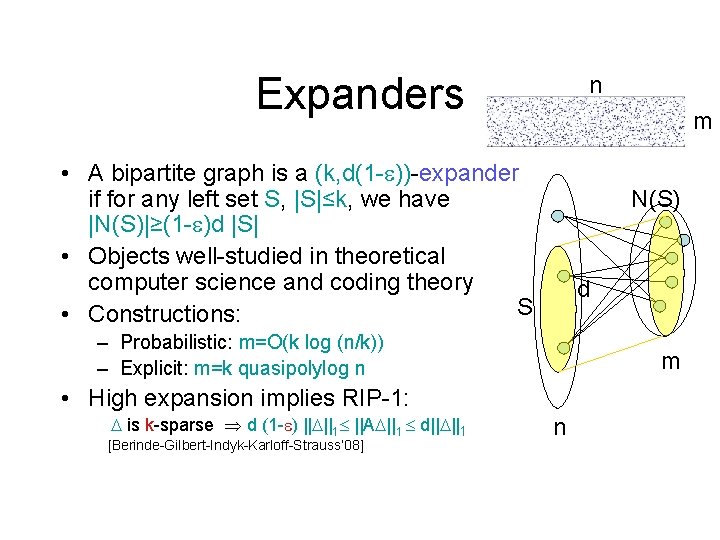
dense • • vs. sparse Restricted Isometry Property (RIP) [Candes-Tao’ 04] is k-sparse || ||2 ||A ||2 C || ||2 Consider m x n 0 -1 matrices with d ones per column Do they satisfy RIP ? – No, unless m= (k 2) [Chandar’ 07] However, they can satisfy the following RIP-1 property [Berinde-Gilbert-Indyk-Karloff -Strauss’ 08]: is k-sparse d (1 - ) || ||1 ||A ||1 d|| ||1 • Sufficient (and necessary) condition: the underlying graph is a ( k, d(1 - /2) )-expander

Expanders n m • A bipartite graph is a (k, d(1 - ))-expander if for any left set S, |S|≤k, we have |N(S)|≥(1 - )d |S| • Objects well-studied in theoretical computer science and coding theory S • Constructions: N(S) d – Probabilistic: m=O(k log (n/k)) – Explicit: m=k quasipolylog n m • High expansion implies RIP-1: is k-sparse d (1 - ) || ||1 ||A ||1 d|| ||1 [Berinde-Gilbert-Indyk-Karloff-Strauss’ 08] n

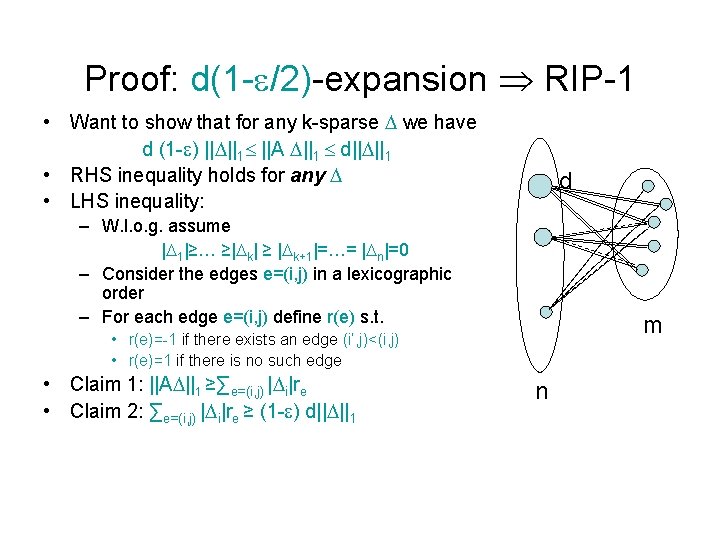
Proof: d(1 - /2)-expansion RIP-1 • Want to show that for any k-sparse we have d (1 - ) || ||1 ||A ||1 d|| ||1 • RHS inequality holds for any • LHS inequality: d – W. l. o. g. assume | 1|≥… ≥| k| ≥ | k+1|=…= | n|=0 – Consider the edges e=(i, j) in a lexicographic order – For each edge e=(i, j) define r(e) s. t. m • r(e)=-1 if there exists an edge (i’, j)<(i, j) • r(e)=1 if there is no such edge • Claim 1: ||A ||1 ≥∑e=(i, j) | i|re • Claim 2: ∑e=(i, j) | i|re ≥ (1 - ) d|| ||1 n

Recovery: algorithms

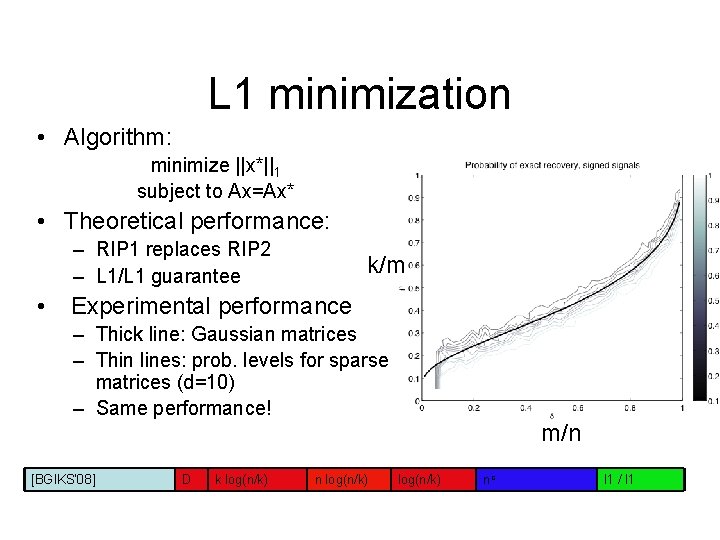
L 1 minimization • Algorithm: minimize ||x*||1 subject to Ax=Ax* • Theoretical performance: – RIP 1 replaces RIP 2 – L 1/L 1 guarantee • k/m Experimental performance – Thick line: Gaussian matrices – Thin lines: prob. levels for sparse matrices (d=10) – Same performance! [BGIKS’ 08] D k log(n/k) n log(n/k) m/n log(n/k) nc l 1 / l 1

Matching Pursuit(s) A x*-x i Ax-Ax* = i • Iterative algorithm: given current approximation x* : – Find (possibly several) i s. t. Ai “correlates” with Ax-Ax*. This yields i and z s. t. ||x*+zei-x||p << ||x* - x||p – Update x* – Sparsify x* (keep only k largest entries) – Repeat • Norms: – p=2 : Co. Sa. MP, SP, IHT etc (RIP) – p=1 : SMP, SSMP (RIP-1) – p=0 : LDPC bit flipping (sparse matrices)

Sequential Sparse Matching Pursuit [Berinde-Indyk’ 09] • Algorithm: – x*=0 – Repeat T times A • Repeat S=O(k) times – Find i and z that minimize* ||A(x*+zei)-Ax||1 – x* = x*+zei i N(i) • Sparsify x* (set all but k largest entries of x* to 0) • Similar to SMP, but updates done sequentially Ax-Ax* x-x* * Set z=median[ (Ax*-Ax)N(I). Instead, one could first optimize (gradient) i and then z [ Fuchs’ 09]

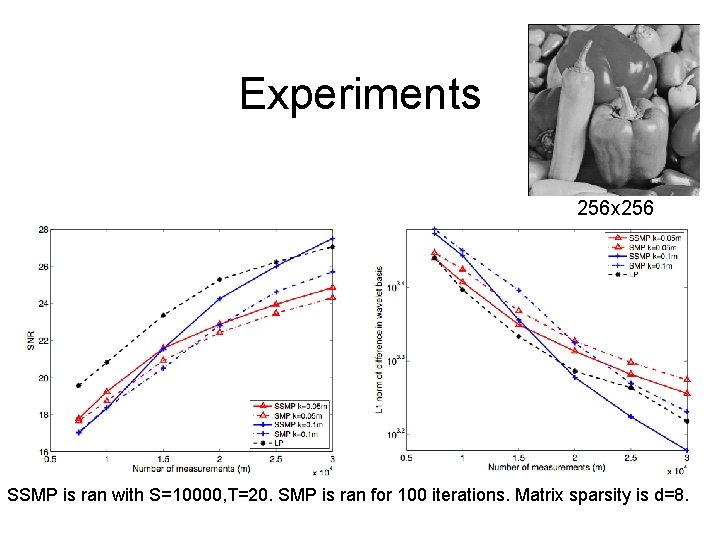
Experiments 256 x 256 SSMP is ran with S=10000, T=20. SMP is ran for 100 iterations. Matrix sparsity is d=8.

Conclusions • Sparse approximation using sparse matrices • State of the art: deterministically can do 2 out of 3: – Near-linear encoding/decoding This talk – O(k log (n/k)) measurements – Approximation guarantee with respect to L 2/L 1 norm • Open problems: – 3 out of 3 ? – Explicit constructions ?

References • Survey: A. Gilbert, P. Indyk, “Sparse recovery using sparse matrices”, Proceedings of IEEE, June 2010. • Courses: – “Streaming, sketching, and sub-linear space algorithms”, Fall’ 07 – “Sub-linear algorithms” (with Ronitt Rubinfeld), Fall’ 10 • Blogs: – Nuit blanche: nuit-blanche. blogspot. com/