Programming Application in Civil Engineering Application of Data

Programming Application in Civil Engineering - Application of Data Structure

Sparse Matrix • Matrices with relatively high proportion of zero or null entries are called sparse matrices. • When matrices are sparse, then much space and computing time could be saved if the non-zero entries were stored explicitly i. e. ignoring the zero entries the processing time and space can be minimized in sparse matrices. • • • In this matrix we have 6 rows and 7 columns. There are 5 nonzero entries out of 42 entries. It requires an alternate form to represent the matrix without considering the null entries.

• The alternate data structure that we consider to represent a sparse matrix is a triplet. • The triplet is a two dimensional array having t+1 rows and 3 columns. Where, t is total number of nonzero entries. • The first row of the triplet contains number of rows, columns and nonzero entries available in the matrix in its 1 st, 2 nd and 3 rd column respectively. Second row onwards it contains the row subscript, column subscript and the value of the nonzero entry in its 1 st, 2 nd and 3 rd column respectively. • Let us represent the above matrix in the following triplet of 6 rows and 3 columns • The above triplet contains only non-zero details by reducing the space for null entries.

Application of Linked List • Sparse Matrix Representation • Polynomial Representation • Dynamic Storage Management

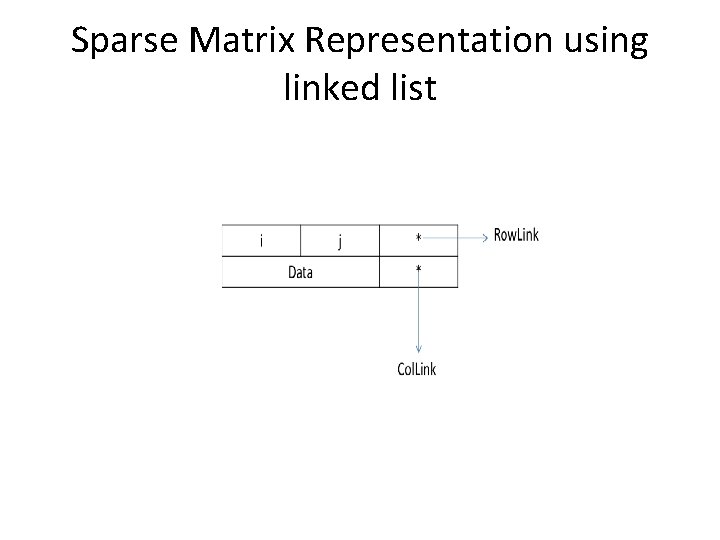
Sparse Matrix Representation using linked list

struct node { int row; int col; int data; struct node *link; }*head=NULL, *curr=NULL, *p=NULL; main() { m=no. of rows n=no. of columns for(i=0; i<m; i++) { for(j=0; j<n; j++) { scanf("%d", &a[i][j]); if(a[i][j]!=0) {

curr=(struct node*)malloc(sizeof(struct node)); curr->row=i; curr->col=j; curr->data=a[i][j]; curr->link=NULL; if(head==NULL) head=curr; else { p=head; while(p->link!=NULL) p=p->link; p->link=curr; } }//end of inner for loop }//end of outer for loop

p=head; if(head==NULL) printf("n. Sparse matrix empty!n"); else { while(p->link!=NULL) { printf("%d %d %d ", p->row, p->col, p->data); p=p->link; } printf("%d %d %d ", p->row, p->col, p->data); } }// end of main

Polynomial Representation • We want to represent the polynomial : • We will represent each term as a node containing coefficient and exponent fields, as well as a pointer to the next term. • Declarations: typedef struct poly_node *poly_pointer; typedef struct poly_node { int coef; int expon; poly_pointer link; };

Application of Stack • • Parenthesis Matching Tower of Hanoi Problem Quick Sort Recursion

Application: Parenthesis Matching • Problem: match the left and right parentheses in a character string • (a*(b+c)+d) – Left parentheses: position 0 and 3 – Right parentheses: position 7 and 10 – Left at position 0 matches with right at position 10 • (a+b))*((c+d) – (0, 4) – Right parenthesis at 5 has no matching left parenthesis – (8, 12) – Left parenthesis at 7 has no matching right parenthesis 15

Parenthesis Matching • (((a+b)*c+d-e)/(f+g)-(h+j)*(k-1))/(m-n) – Output pairs (u, v) such that the left parenthesis at position u is matched with the right parenthesis at v. (2, 6) (1, 13) (15, 19) (21, 25) (27, 31) (0, 32) (34, 38) • How do we implement this using a stack? 1. Scan expression from left to right 2. When a left parenthesis is encountered, add its position to the stack 3. When a right parenthesis is encountered, remove matching position from the stack 16

Example of Parenthesis Matching (((a+b)*c+d-e)/(f+g)-(h+j)*(k-1))/(m-n) stack 2 1 0 output – … 1 0 0 (2, 6) (1, 13) 15 0 0 (15, 19) 21 0 0 (21, 25) … Do the same for (a-b)*(c+d/(e-f))/(g+h) 17

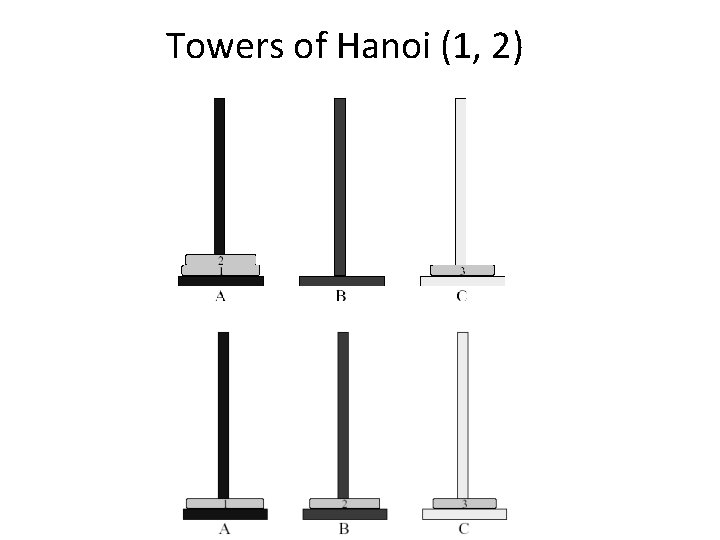
Application: Towers of Hanoi • Read the ancient Tower of Brahma ritual • n disks to be moved from tower A to tower C with the following restrictions: – Move 1 disk at a time – Cannot place larger disk on top of a smaller one 18

Let’s solve the problem for 3 disks 19

Towers of Hanoi (1, 2) 20

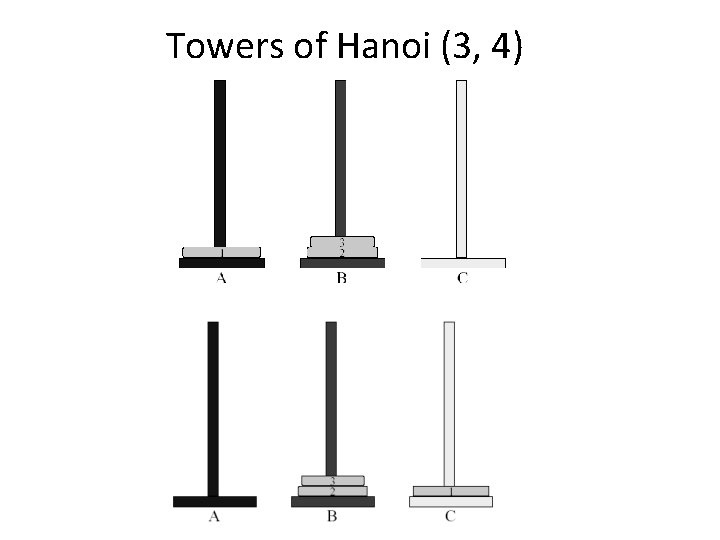
Towers of Hanoi (3, 4) 21

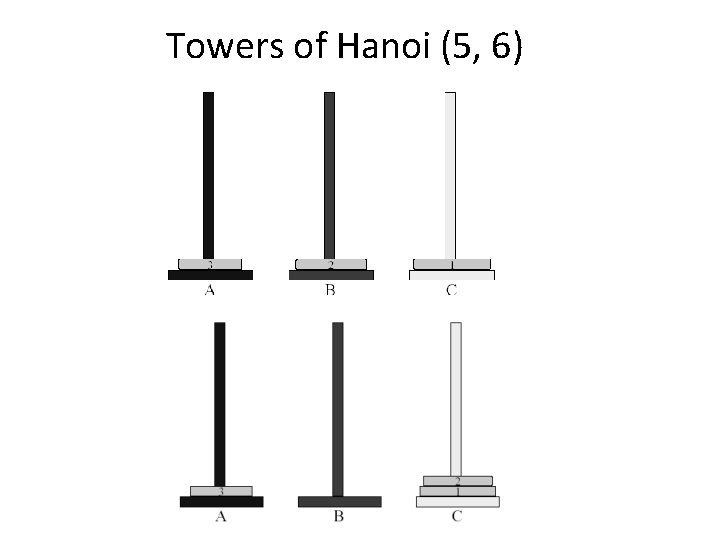
Towers of Hanoi (5, 6) 22

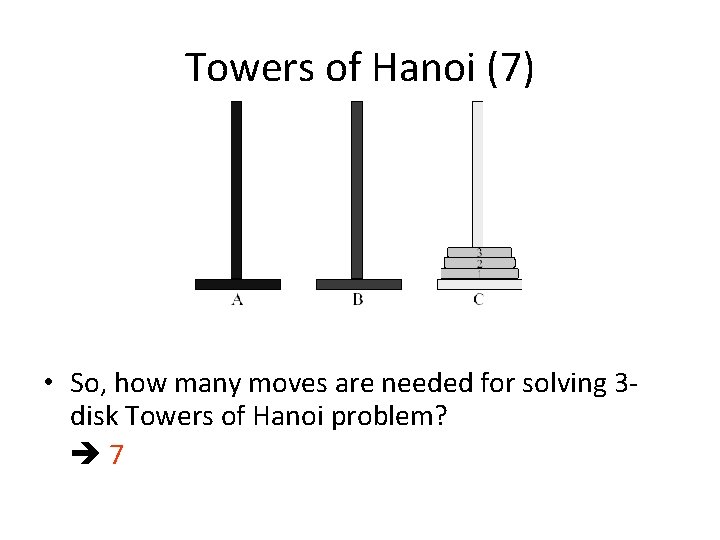
Towers of Hanoi (7) • So, how many moves are needed for solving 3 disk Towers of Hanoi problem? 7 23

Time complexity for Towers of Hanoi • A very elegant solution is to use recursion. • The minimum number of moves required is 2 n-1 • Time complexity for Towers of Hanoi is Q(2 n), which is exponential! • Since disks are removed from each tower in a LIFO manner, each tower can be represented as a stack 24

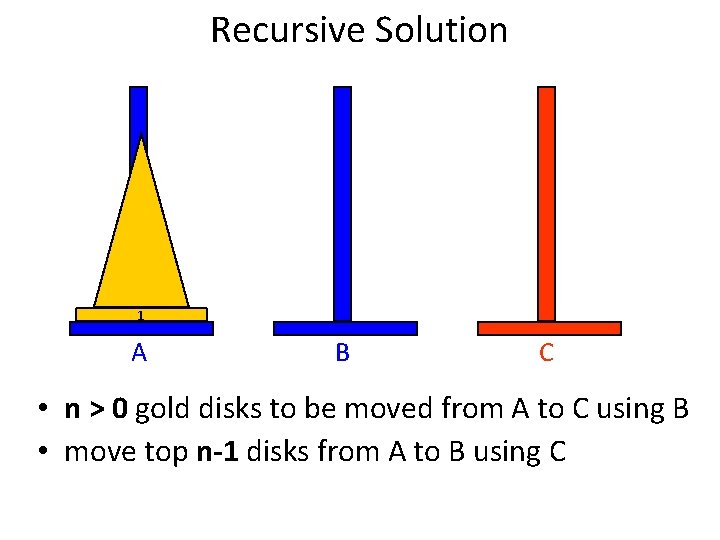
Recursive Solution 1 A B C • n > 0 gold disks to be moved from A to C using B • move top n-1 disks from A to B using C 25

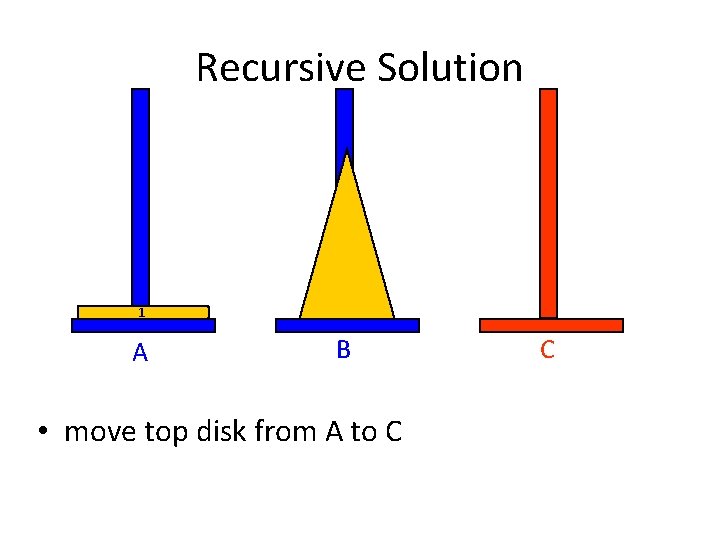
Recursive Solution 1 A B C • move top disk from A to C 26

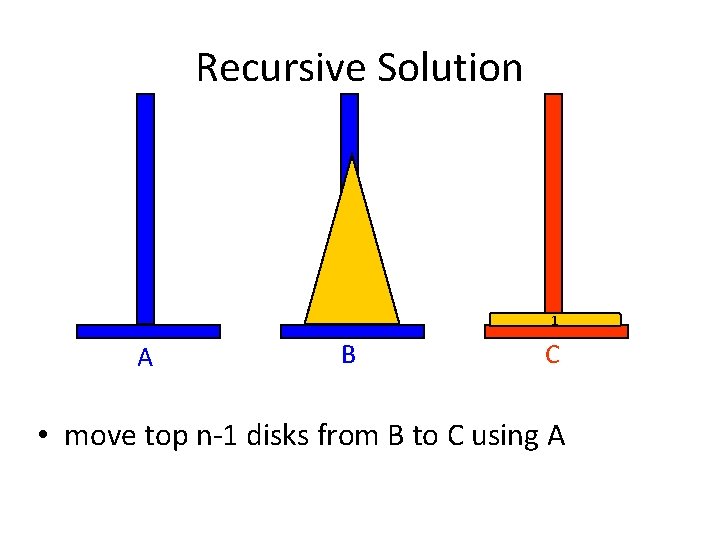
Recursive Solution 1 A B C • move top n-1 disks from B to C using A 27

Recursive Solution • To move n rings from A to C using B as spare: • if n is 1 – just do it, • otherwise. . . – move n-1 rings from A to B using C as spare – move one ring from A to C – move n-1 rings from B to C using A as spare 28

#include <stdio. h> int n, A, B, C; /* number to move, source pole, destination pole and spare pole respectively */ void move(n, A, C, B) { if (n==1) { printf("Move from %d to %d. n", A, C); } else { move(n-1, A, B, C); move(1, A, C, B); move(n-1, B, C, A); } } main() { move(4, 1, 3, 2); }