Solicitacin por Flexin Simple Resolucin del Ejercicio N

Solicitación por Flexión Simple Resolución del Ejercicio N° 1 (Ejercicio II del Complemento Teórico) Curso de Estabilidad IIb Ing. Gabriel Pujol Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la Facultad de Ingeniería de la Universidad de Buenos Aires

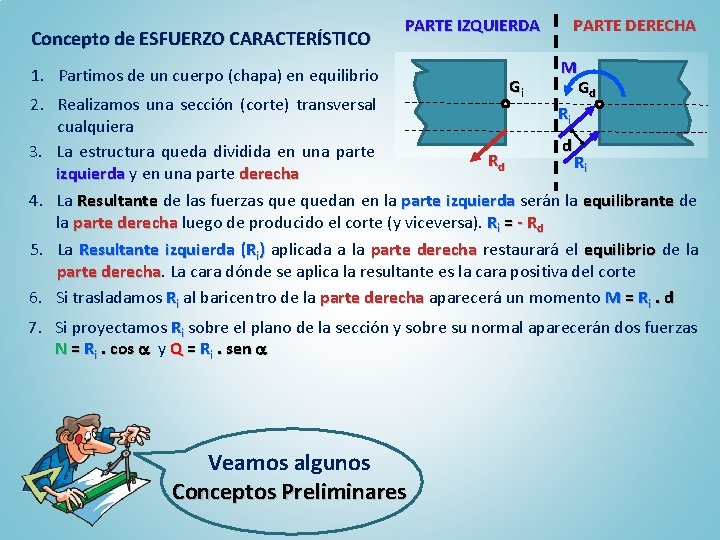
Concepto de ESFUERZO CARACTERÍSTICO PARTE IZQUIERDA 1. Partimos de un cuerpo (chapa) en equilibrio Gi PARTE DERECHA M Gd 2. Realizamos una sección (corte) transversal Ri cualquiera d 3. La estructura queda dividida en una parte Rd Ri izquierda y en una parte derecha 4. La Resultante de las fuerzas quedan en la parte izquierda serán la equilibrante de la parte derecha luego de producido el corte (y viceversa). Ri = - Rd 5. La Resultante izquierda (Ri) aplicada a la parte derecha restaurará el equilibrio de la parte derecha La cara dónde se aplica la resultante es la cara positiva del corte 6. Si trasladamos Ri al baricentro de la parte derecha aparecerá un momento M = Ri. d 7. Si proyectamos Ri sobre el plano de la sección y sobre su normal aparecerán dos fuerzas N = Ri. cos y Q = Ri. sen Veamos algunos Conceptos Preliminares

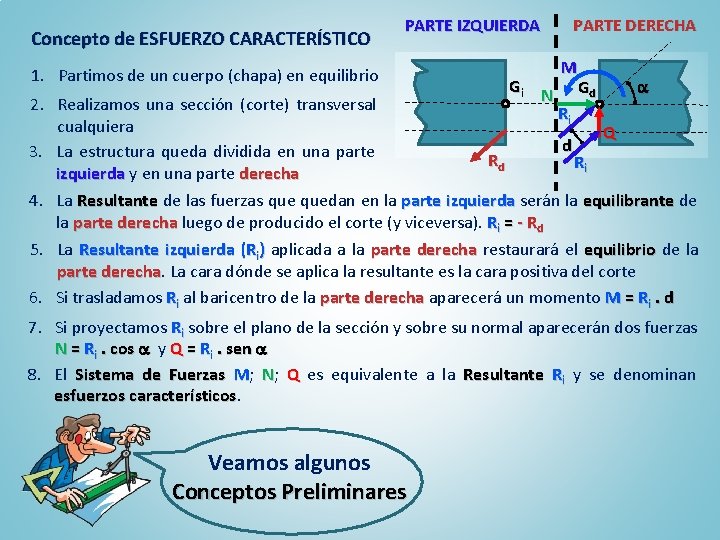
Concepto de ESFUERZO CARACTERÍSTICO PARTE IZQUIERDA 1. Partimos de un cuerpo (chapa) en equilibrio Gi N PARTE DERECHA M Gd 2. Realizamos una sección (corte) transversal Ri cualquiera Q d 3. La estructura queda dividida en una parte Rd Ri izquierda y en una parte derecha 4. La Resultante de las fuerzas quedan en la parte izquierda serán la equilibrante de la parte derecha luego de producido el corte (y viceversa). Ri = - Rd 5. La Resultante izquierda (Ri) aplicada a la parte derecha restaurará el equilibrio de la parte derecha La cara dónde se aplica la resultante es la cara positiva del corte 6. Si trasladamos Ri al baricentro de la parte derecha aparecerá un momento M = Ri. d 7. Si proyectamos Ri sobre el plano de la sección y sobre su normal aparecerán dos fuerzas N = Ri. cos y Q = Ri. sen 8. El Sistema de Fuerzas M; N; Q es equivalente a la Resultante Ri y se denominan esfuerzos característicos Veamos algunos Conceptos Preliminares

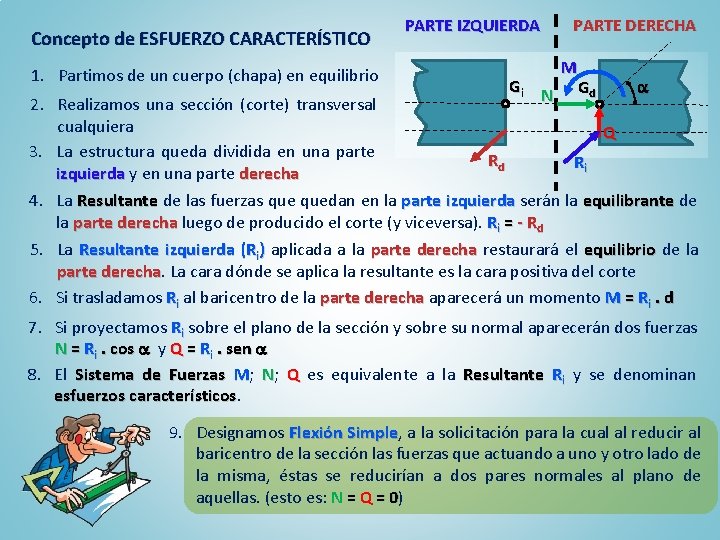
Concepto de ESFUERZO CARACTERÍSTICO 1. Partimos de un cuerpo (chapa) en equilibrio PARTE IZQUIERDA Gi N PARTE DERECHA M Gd 2. Realizamos una sección (corte) transversal cualquiera Q 3. La estructura queda dividida en una parte Rd Ri izquierda y en una parte derecha 4. La Resultante de las fuerzas quedan en la parte izquierda serán la equilibrante de la parte derecha luego de producido el corte (y viceversa). Ri = - Rd 5. La Resultante izquierda (Ri) aplicada a la parte derecha restaurará el equilibrio de la parte derecha La cara dónde se aplica la resultante es la cara positiva del corte 6. Si trasladamos Ri al baricentro de la parte derecha aparecerá un momento M = Ri. d 7. Si proyectamos Ri sobre el plano de la sección y sobre su normal aparecerán dos fuerzas N = Ri. cos y Q = Ri. sen 8. El Sistema de Fuerzas M; N; Q es equivalente a la Resultante Ri y se denominan esfuerzos característicos 9. Designamos Flexión Simple, Simple a la solicitación para la cual al reducir al baricentro de la sección las fuerzas que actuando a uno y otro lado de la misma, éstas se reducirían a dos pares normales al plano de aquellas. (esto es: N = Q = 0) 0

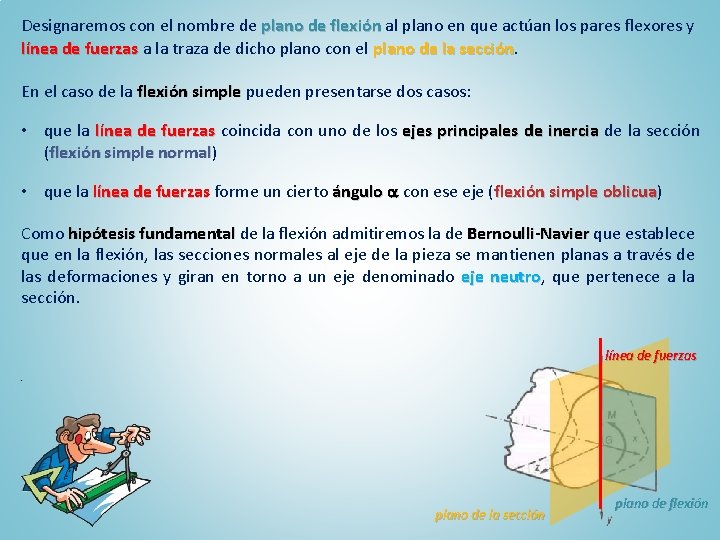
Designaremos con el nombre de plano de flexión al plano en que actúan los pares flexores y línea de fuerzas a la traza de dicho plano con el plano de la sección En el caso de la flexión simple pueden presentarse dos casos: • que la línea de fuerzas coincida con uno de los ejes principales de inercia de la sección (flexión simple normal) normal • que la línea de fuerzas forme un cierto ángulo con ese eje (flexión simple oblicua) oblicua Como hipótesis fundamental de la flexión admitiremos la de Bernoulli-Navier que establece que en la flexión, las secciones normales al eje de la pieza se mantienen planas a través de las deformaciones y giran en torno a un eje denominado eje neutro, neutro que pertenece a la sección. línea de fuerzas. plano de la sección plano de flexión

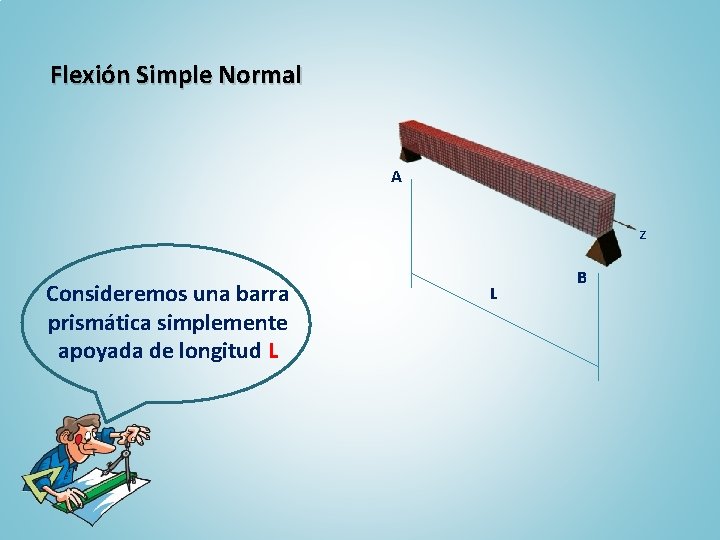
Flexión Simple Normal A z Consideremos una barra prismática simplemente apoyada de longitud L L B

z Carguémosla con 2 fuerzas iguales manteniendo la simetría de cargas

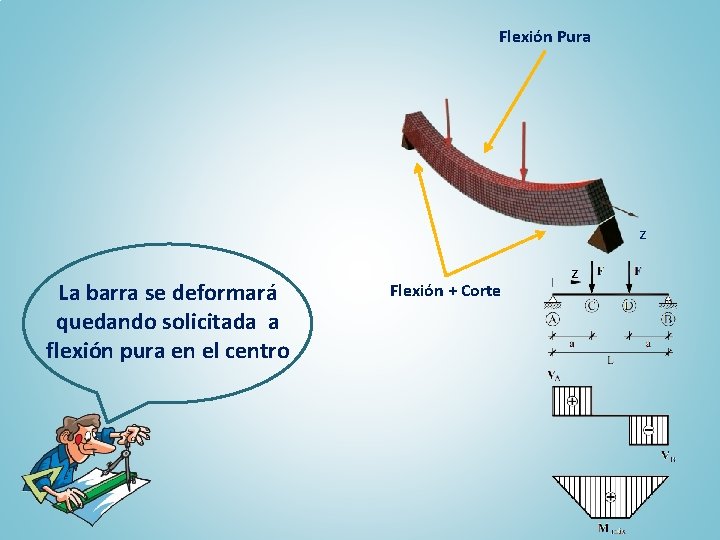
Flexión Pura z La barra se deformará quedando solicitada a flexión pura en el centro Flexión + Corte z

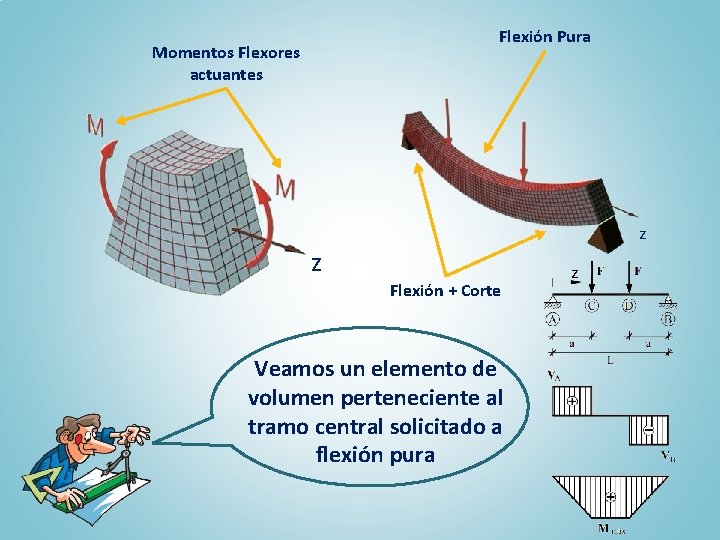
Flexión Pura Momentos Flexores actuantes z z Flexión + Corte Veamos un elemento de volumen perteneciente al tramo central solicitado a flexión pura z

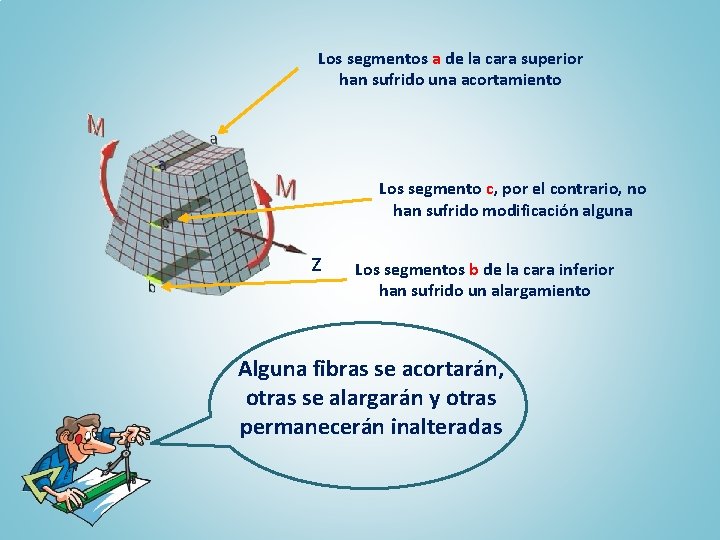
Los segmentos a de la cara superior han sufrido una acortamiento Los segmento c, por el contrario, no han sufrido modificación alguna z Los segmentos b de la cara inferior han sufrido un alargamiento Alguna fibras se acortarán, otras se alargarán y otras permanecerán inalteradas

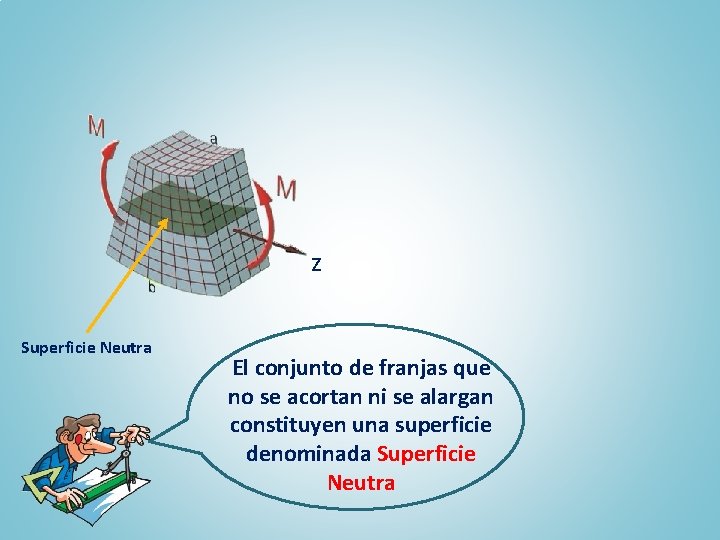
z Superficie Neutra El conjunto de franjas que no se acortan ni se alargan constituyen una superficie denominada Superficie Neutra

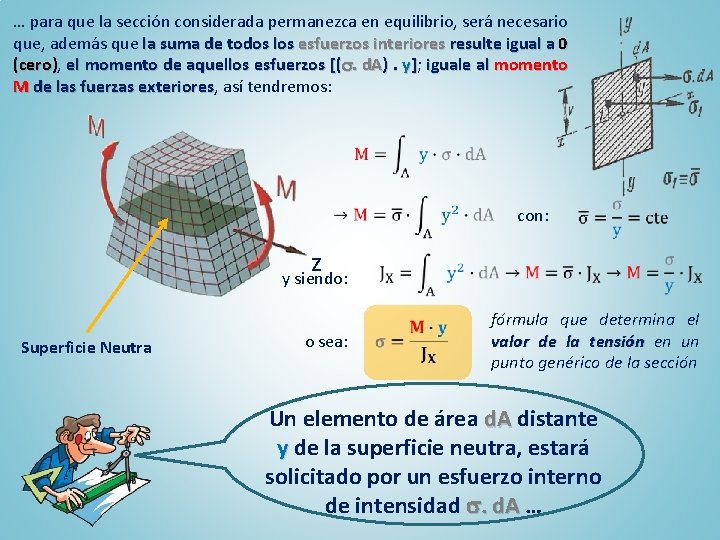
… para que la sección considerada permanezca en equilibrio, será necesario que, además que la suma de todos los esfuerzos interiores resulte igual a 0 (cero), (cero) el momento de aquellos esfuerzos [(. d. A). y]; iguale al momento M de las fuerzas exteriores, exteriores así tendremos: con: z y siendo: Superficie Neutra o sea: fórmula que determina el valor de la tensión en un punto genérico de la sección Un elemento de área d. A distante y de la superficie neutra, estará solicitado por un esfuerzo interno de intensidad . d. A …

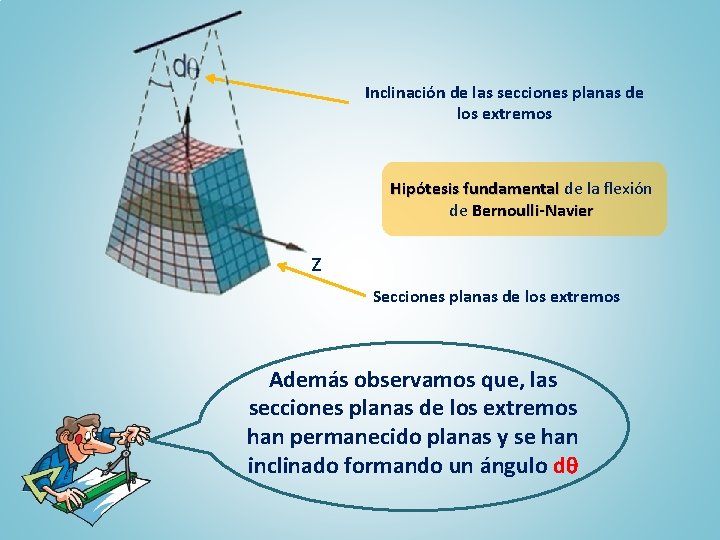
Inclinación de las secciones planas de los extremos Hipótesis fundamental de la flexión de Bernoulli-Navier z Secciones planas de los extremos Además observamos que, las secciones planas de los extremos han permanecido planas y se han inclinado formando un ángulo dq

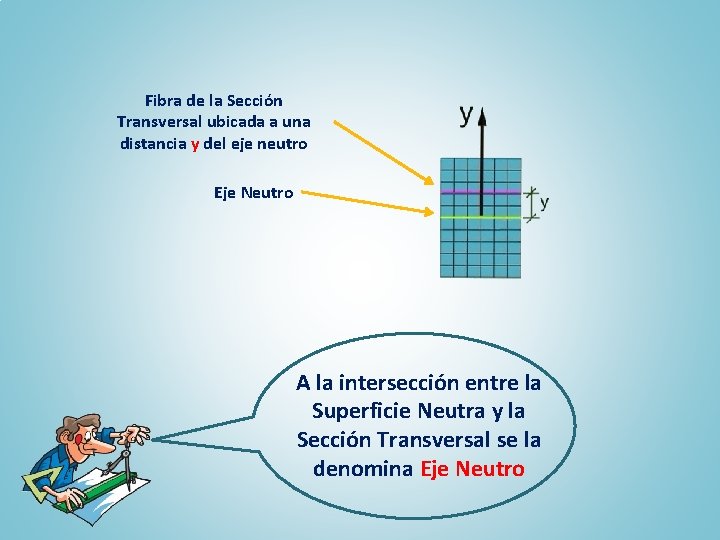
Fibra de la Sección Transversal ubicada a una distancia y del eje neutro Eje Neutro A la intersección entre la Superficie Neutra y la Sección Transversal se la denomina Eje Neutro

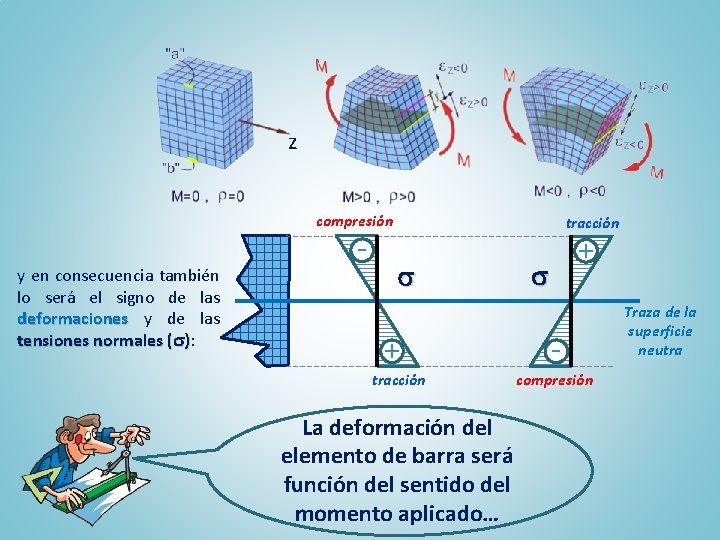
z z z compresión y en consecuencia también lo será el signo de las deformaciones y de las tensiones normales ( ): - tracción + tracción La deformación del elemento de barra será función del sentido del momento aplicado… + compresión Traza de la superficie neutra

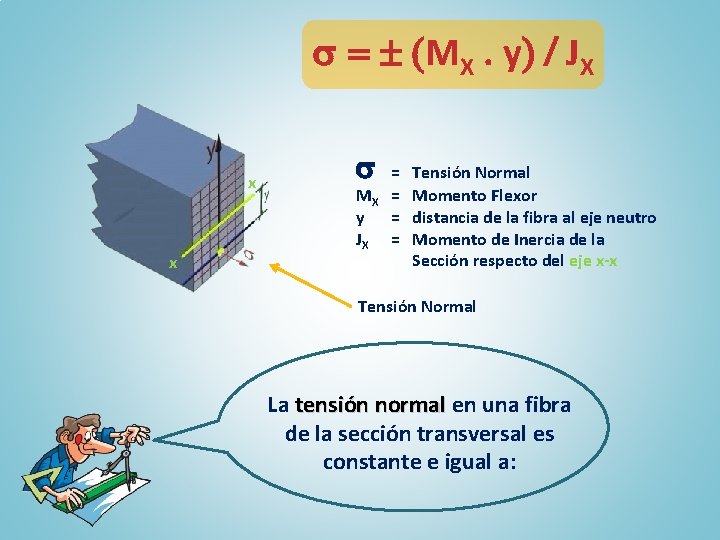
= (MX. y) / JX x x MX y JX = = Tensión Normal Momento Flexor distancia de la fibra al eje neutro Momento de Inercia de la Sección respecto del eje x-x Tensión Normal La tensión normal en una fibra de la sección transversal es constante e igual a:

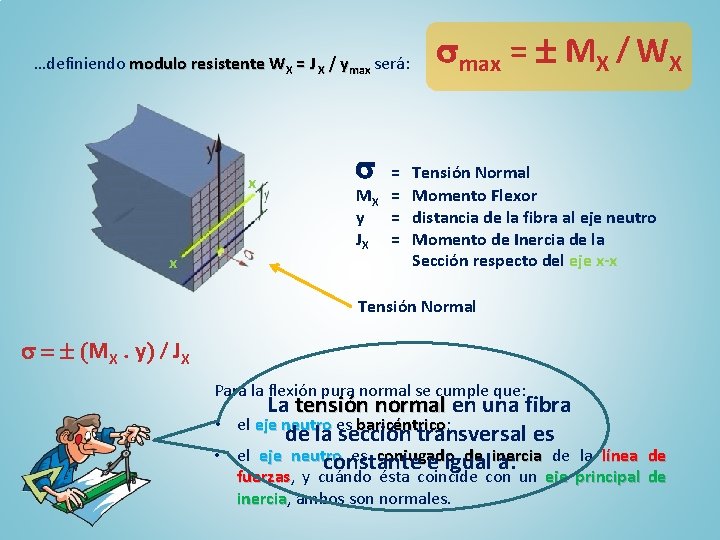
…definiendo modulo resistente WX = J X / ymax será: x x MX y JX = = max = MX / WX Tensión Normal Momento Flexor distancia de la fibra al eje neutro Momento de Inercia de la Sección respecto del eje x-x Tensión Normal = (MX. y) / JX Para la flexión pura normal se cumple que: • • La tensión normal en una fibra el eje neutro es baricéntrico; baricéntrico de la sección transversal es el eje neutro es conjugado de inercia constante e igual a: de la línea de fuerzas, fuerzas y cuándo ésta coincide con un eje principal de inercia, inercia ambos son normales.

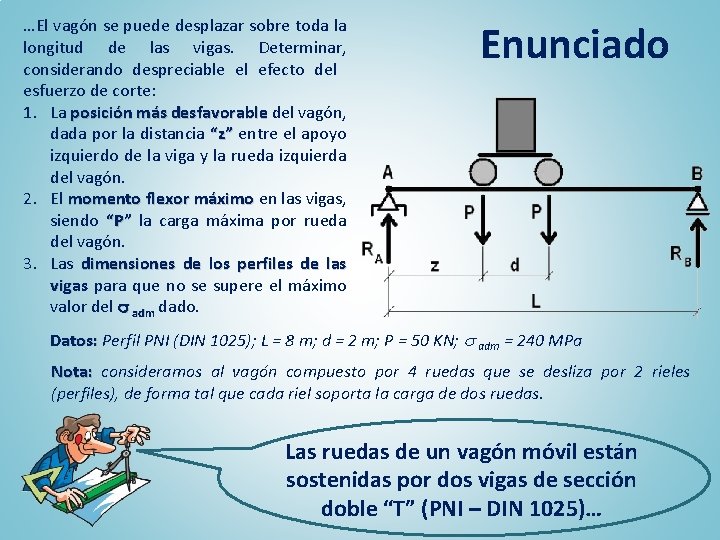
…El vagón se puede desplazar sobre toda la longitud de las vigas. Determinar, considerando despreciable el efecto del esfuerzo de corte: 1. La posición más desfavorable del vagón, dada por la distancia “z” entre el apoyo izquierdo de la viga y la rueda izquierda del vagón. 2. El momento flexor máximo en las vigas, siendo “P” la carga máxima por rueda del vagón. 3. Las dimensiones de los perfiles de las vigas para que no se supere el máximo valor del adm dado. Enunciado Datos: Perfil PNI (DIN 1025); L = 8 m; d = 2 m; P = 50 KN; adm = 240 MPa Nota: consideramos al vagón compuesto por 4 ruedas que se desliza por 2 rieles (perfiles), de forma tal que cada riel soporta la carga de dos ruedas. Las ruedas de un vagón móvil están sostenidas por dos vigas de sección doble “T” (PNI – DIN 1025)…

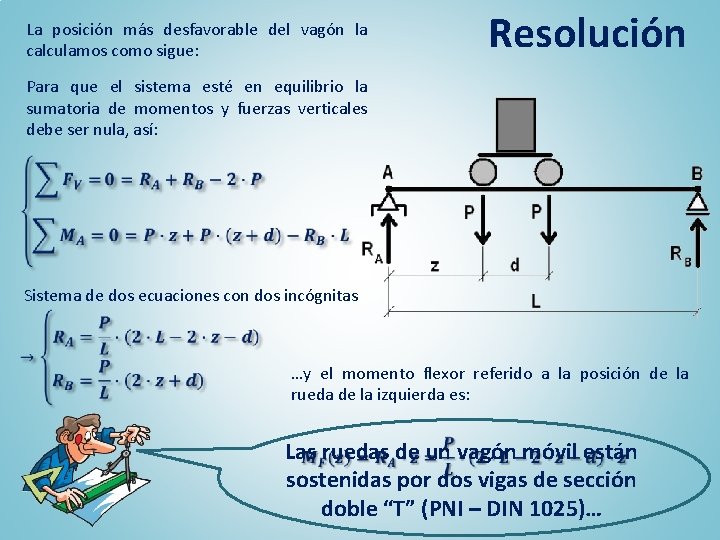
La posición más desfavorable del vagón la calculamos como sigue: Resolución Para que el sistema esté en equilibrio la sumatoria de momentos y fuerzas verticales debe ser nula, así: Sistema de dos ecuaciones con dos incógnitas …y el momento flexor referido a la posición de la rueda de la izquierda es: Las ruedas de un vagón móvil están sostenidas por dos vigas de sección doble “T” (PNI – DIN 1025)…

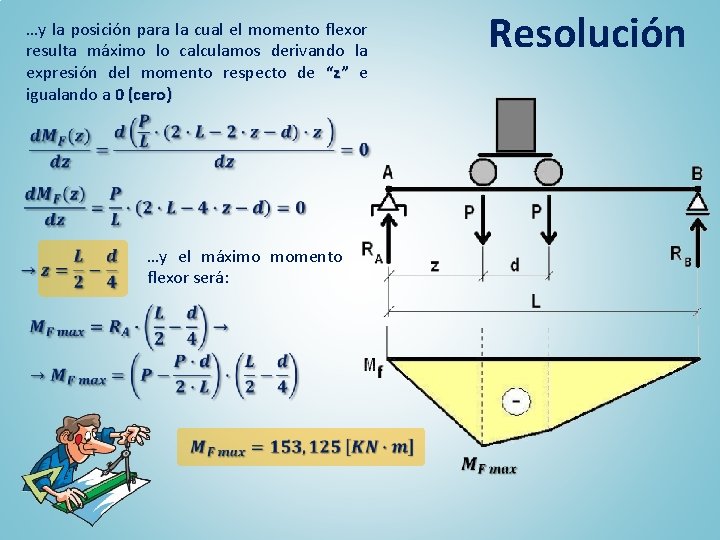
…y la posición para la cual el momento flexor resulta máximo lo calculamos derivando la expresión del momento respecto de “z” e igualando a 0 (cero) …y el máximo momento flexor será: Resolución

Dimensionamos el perfil, para ello calculamos el valor del módulo resistente: Vamos a la tabla de perfiles (DIN 1025), 1025) entramos con por la columna Wx y seleccionamos un perfil que tenga un módulo resistente mayor o igual al calculado, así seleccionamos: Resolución

Bibliografía Estabilidad II - E. Fliess Introducción a la estática y resistencia de materiales - C. Raffo Mecánica de materiales - F. Beer y otros Resistencia de materiales - R. Abril / C. Benítez Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana Resistencia de materiales - V. Feodosiev Resistencia de materiales - A. Pytel / F. Singer Resistencia de materiales - S. Timoshenko

Muchas Gracias