Slopes and Areas Frequently we will want to









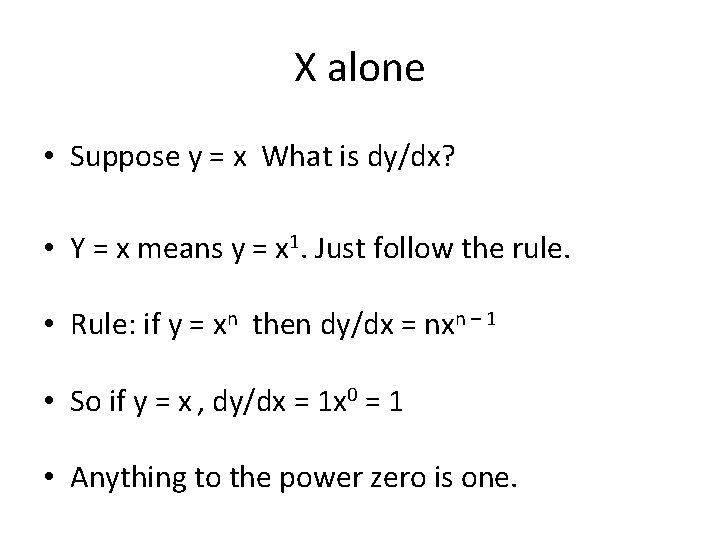











- Slides: 33

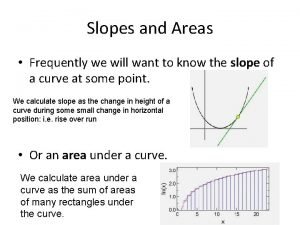
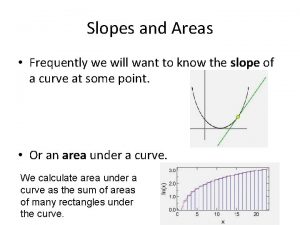
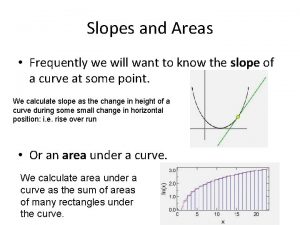
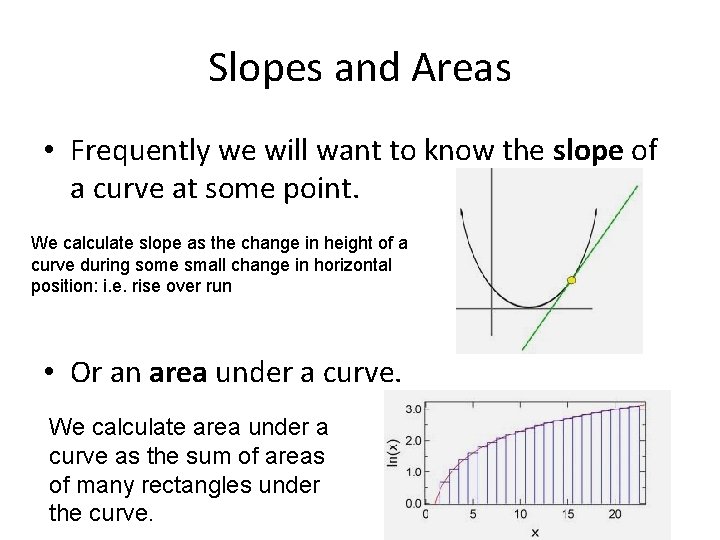
Slopes and Areas • Frequently we will want to know the slope of a curve at some point. We calculate slope as the change in height of a curve during some small change in horizontal position: i. e. rise over run • Or an area under a curve. We calculate area under a curve as the sum of areas of many rectangles under the curve.

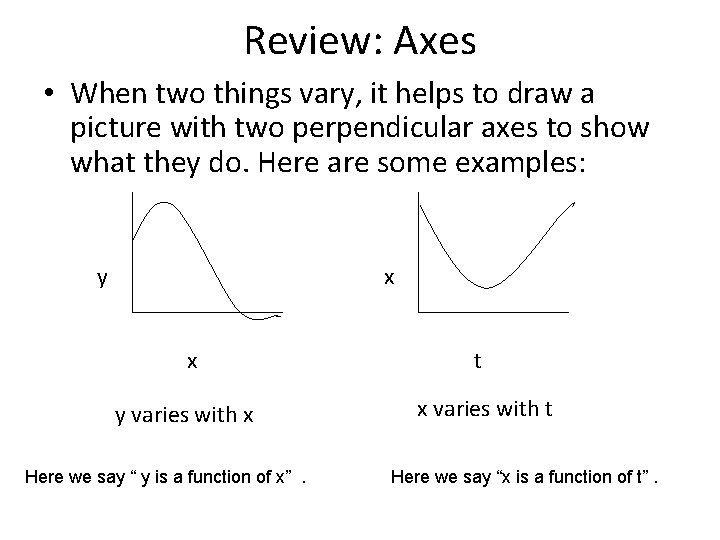
Review: Axes • When two things vary, it helps to draw a picture with two perpendicular axes to show what they do. Here are some examples: y x x y varies with x Here we say “ y is a function of x”. t x varies with t Here we say “x is a function of t”.

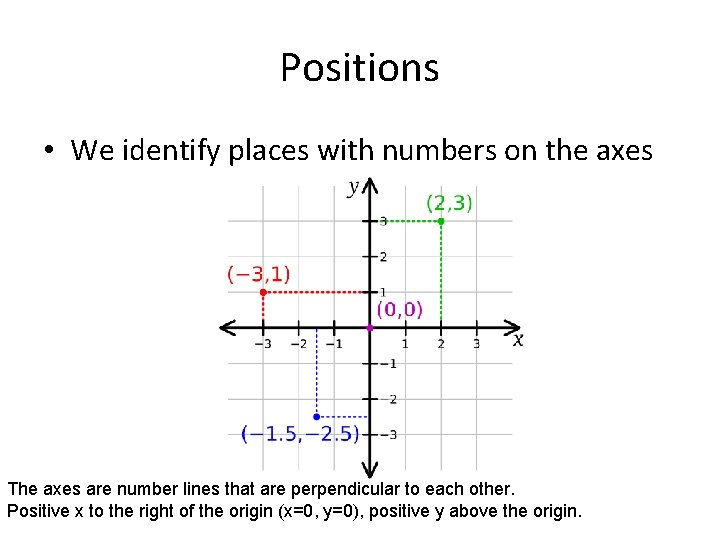
Positions • We identify places with numbers on the axes The axes are number lines that are perpendicular to each other. Positive x to the right of the origin (x=0, y=0), positive y above the origin.

Straight Lines • Sometimes we can write an equation for how one variable varies with the other. For example a straight line can be described as y = ax + b Here, y is a position on the line along the y-axis, x is a position on the line along the xaxis, a is the slope, and b is the place where the line hits the y-axis

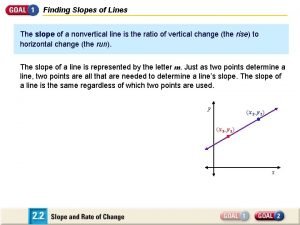
Straight Line Slope y = ax + b The slope, a, is just the rise Dy divided by the run Dx. We can do this anywhere on the line. Proceed in the positive x direction for some number of units, and count the number of units up or down the y changes So the slope of the line here is Dy = -3 2 Dx Remember: Rise over Run and up and right are positive

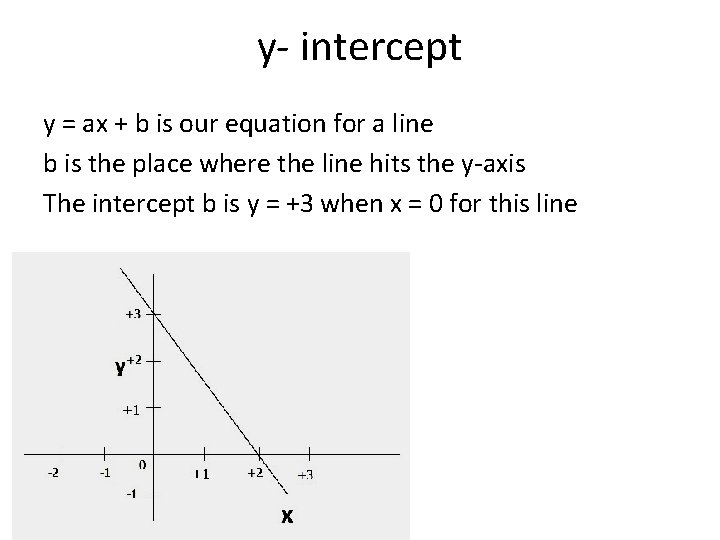
y- intercept y = ax + b is our equation for a line b is the place where the line hits the y-axis The intercept b is y = +3 when x = 0 for this line

y = ax + b is the general equation for a line We want an equation for this line Equation of our example line So the equation of the line here is y = -3 x + 3 2 We plugged in the slope and y intercept

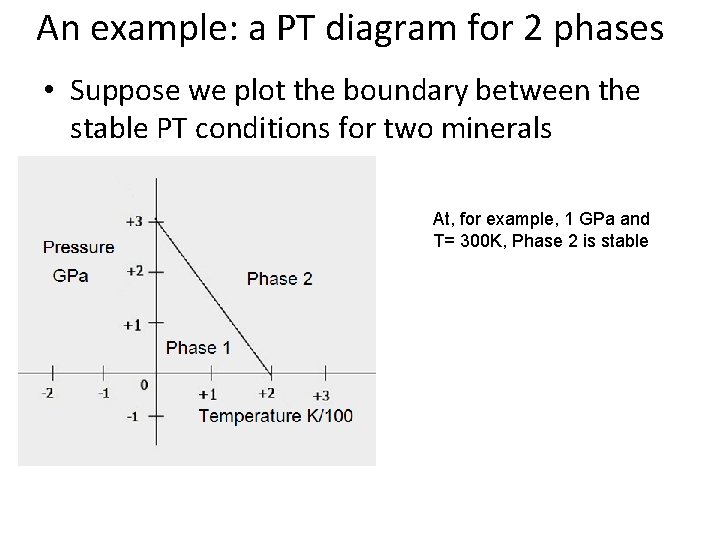
An example: a PT diagram for 2 phases • Suppose we plot the boundary between the stable PT conditions for two minerals At, for example, 1 GPa and T= 300 K, Phase 2 is stable

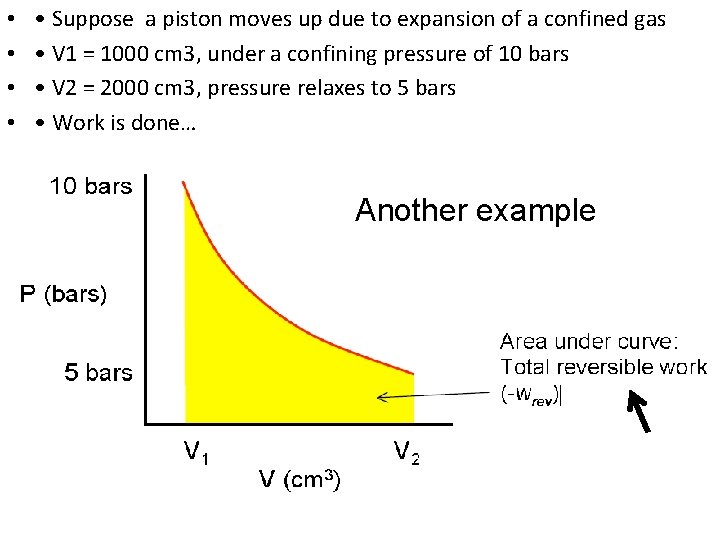
• • • Suppose a piston moves up due to expansion of a confined gas • V 1 = 1000 cm 3, under a confining pressure of 10 bars • V 2 = 2000 cm 3, pressure relaxes to 5 bars • Work is done… Another example

Trig • Perpendicular axes and lines are very handy. Recall we said we use them for vectors such as velocity. To break a vector r into components, we use trig. The rise is r. sin q, and the run is r cos q. Demo: The sine is the ordinate (rise) divided by the hypotenuse sin q = rise / r so the rise = r sin q Similarly the run = r cos q hy run rise se u en t po This vector with size r and direction q, has been broken down into components. Along the y-axis, the rise is Dy = +r sin q Along the x-axis, the run is Dx = +r cos q Whenever possible we work with unit vectors so r = 1, simplifying calculations.

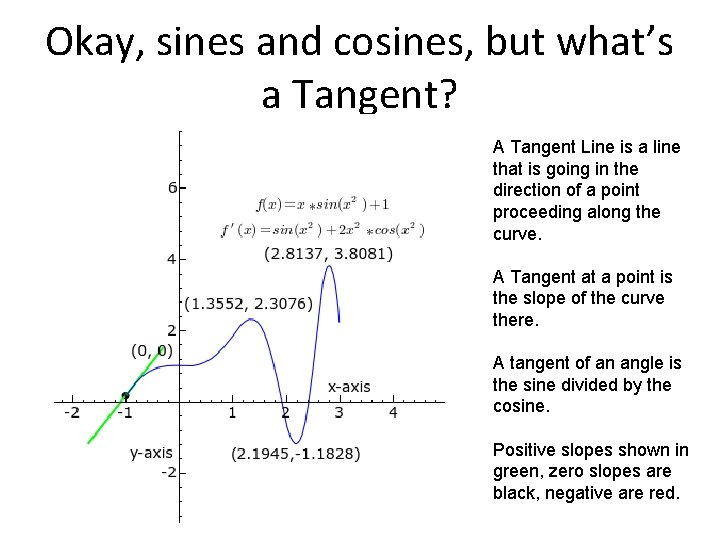
Okay, sines and cosines, but what’s a Tangent? A Tangent Line is a line that is going in the direction of a point proceeding along the curve. A Tangent at a point is the slope of the curve there. A tangent of an angle is the sine divided by the cosine. Positive slopes shown in green, zero slopes are black, negative are red.

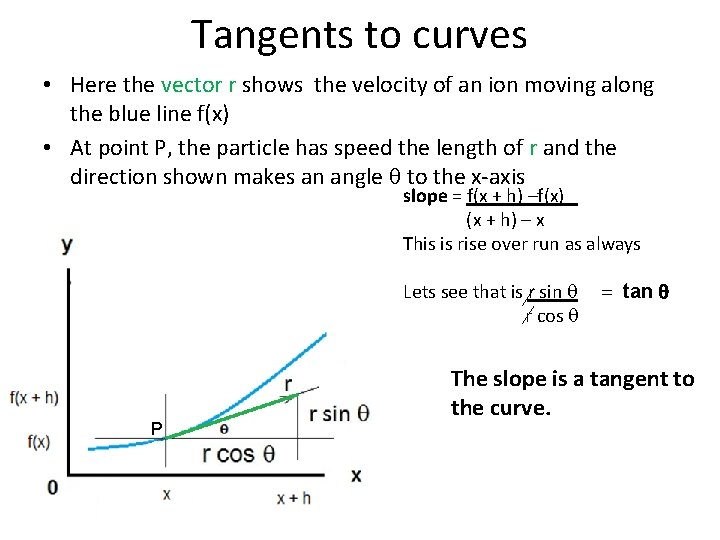
Tangents to curves • Here the vector r shows the velocity of an ion moving along the blue line f(x) • At point P, the particle has speed the length of r and the direction shown makes an angle q to the x-axis slope = f(x + h) –f(x) (x + h) – x This is rise over run as always Lets see that is r sin q r cos q PP = tan q The slope is a tangent to the curve.

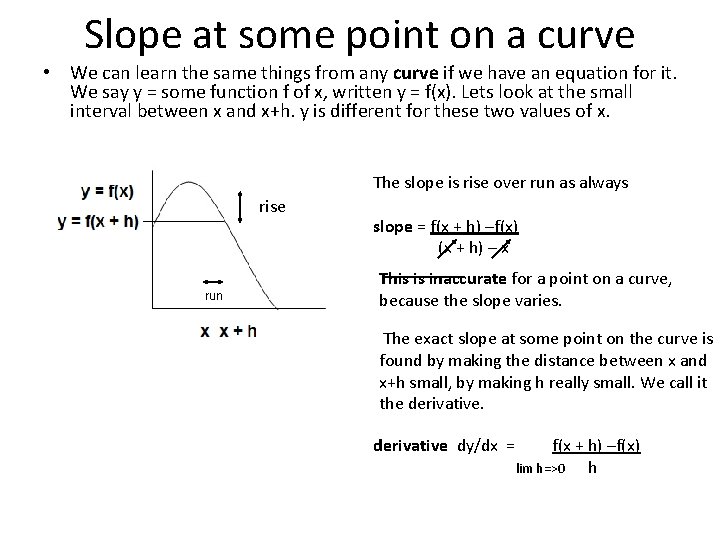
Slope at some point on a curve • We can learn the same things from any curve if we have an equation for it. We say y = some function f of x, written y = f(x). Lets look at the small interval between x and x+h. y is different for these two values of x. The slope is rise over run as always rise run slope = f(x + h) –f(x) (x + h) – x This is inaccurate for a point on a curve, because the slope varies. The exact slope at some point on the curve is found by making the distance between x and x+h small, by making h really small. We call it the derivative dy/dx = f(x + h) –f(x) lim h=>0 h

A simple derivative for Polynomials • The exact slope “derivative” of f(x) f’(x) = f(x + h) – f(x) lim h=>0 (x + h) – x lim h=>0 h is known for all of the types of functions we will use in Petrology. For example, suppose y = xn where n is some constant and x is a variable Then y’(x) = dy/dx = nxn-1 dy/dx means “The small change in y with respect to a small change in x”

We just saw for polynomials y = xn the dy/dx = nxn - 1 Some Examples for Polynomials • (1) Suppose y = x 4. What is dy/dx? dy/dx = 4 x 3 • (2) Suppose y = x-2 What is dy/dx? dy/dx = -2 x-3

Differentials • Those new symbols dy/dx mean the really accurate slope of the function y = f(x) at any point. We say they are algebraic, meaning dx and dy behave like any other variable you manipulated in high school algebra class. • The small change in y at some point on the function (written dy) is a separate entity from dx. • For example, if y = xn • dy/dx = nxn-I also means dy = nxn-I dx

Variable names • There is nothing special about the letters we use except to remind us of the axes in our coordinate system • For example, if y = un • dy = nun-I du is the same as the previous formula. y = un u

Constants Alone • The derivative of a constant is zero. • If y = 17, dy/dx = 0 because constants don’t change, and the constant line has zero slope y 17 Y = 17 x For any dx, dy = 0
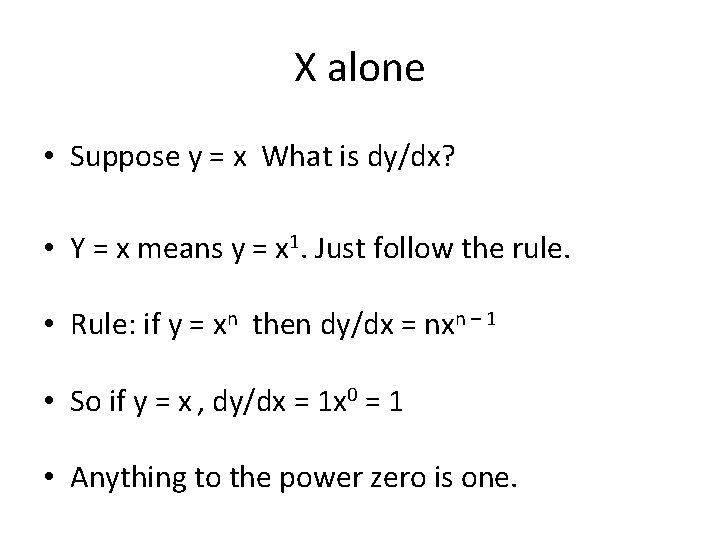
X alone • Suppose y = x What is dy/dx? • Y = x means y = x 1. Just follow the rule. • Rule: if y = xn then dy/dx = nxn – 1 • So if y = x , dy/dx = 1 x 0 = 1 • Anything to the power zero is one.

A Constant times a Polynomial • Suppose y = 4 x 7 What is dy/dx? • Rule: The derivative of a constant times a polynomial is just the constant times the derivative of the polynomial. • So if y = 4 x 7 , dy/dx = 4. ( 7 x 6)

For polynomials y = xn dy/dx = nxn - 1 Multiple Terms in a sum • The derivative of a function with more than one term is the sum of the individual derivatives. • If y = 3 + 2 t + t 2 then dy/dt = 0 + 2 +2 t • Notice 2 t = 2 t 1

The derivative of a product • In words, the derivative of a product of two terms is the first term times the derivative of the second, plus the second term times the derivative of the first.

Exponents Suppose m and n are rational numbers • aman = am+n • (am)n = amn • (a/b)m = am/bm am/an = am-n (ab)m = ambm a-n = 1/an You can remember all of these just by experimenting For example 22 = 2 x 2 and 24= 2 x 2 x 2 x 2 so 22 x 24 = 2 x 2 x 2 x 2 = 26 reminds you of rule 1 Rule 6, a-n = 1/an , is especially useful

Logarithms • Logarithms (Logs) are just exponents • if by = x then y = logb x • log 10 (100) = 2 because 102 = 100 • Natural logs (ln) use e = 2. 718 as a base • For example ln(1) = loge(1) = 0 because e 0 = (2. 718)0 = 1 Anything to the zero power is one.

e • e is a base, the base of the so-called natural logarithms just mentioned. e ~ 2. 718 • It has a very interesting derivative (slope). • Suppose u is some function • Then d(eu) = eu du • “The derivative of eu is eu times the derivative of u” • Example: If y = e 2 x what is dy/dx? • here u = 2 x, so du = 2 • Therefore dy/dx = e 2 x. 2

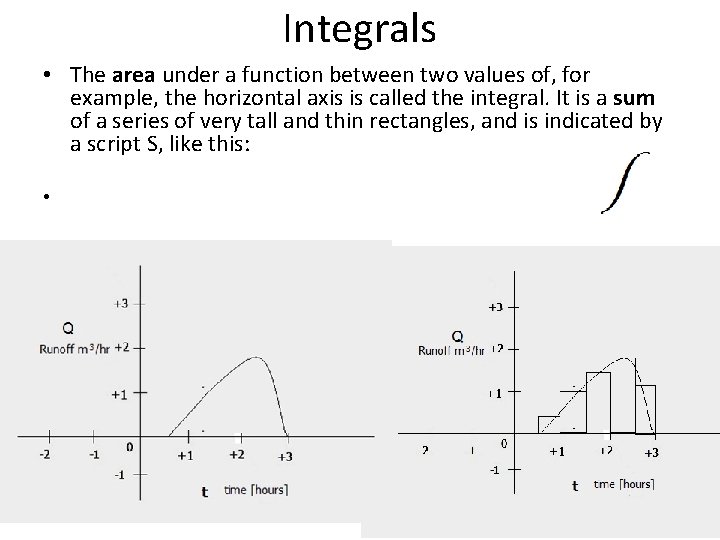
Integrals • The area under a function between two values of, for example, the horizontal axis is called the integral. It is a sum of a series of very tall and thin rectangles, and is indicated by a script S, like this: •

Integrals • To get accuracy with areas we use extremely thin rectangles, much thinner than this.

Example 1 Integration is the inverse operation for differentiation • If y=3 x 5 Then dy/dx = 15 x 4 • Then y = 15 x 4 dx = 3 x 5 + a constant We have to add the constant as a reminder because, if a constant was present in the original function, it’s derivative would be zero and we wouldn’t see it.

Example 2: a trick Sometimes we must multiply by one to get a known integral form. For example, we know:

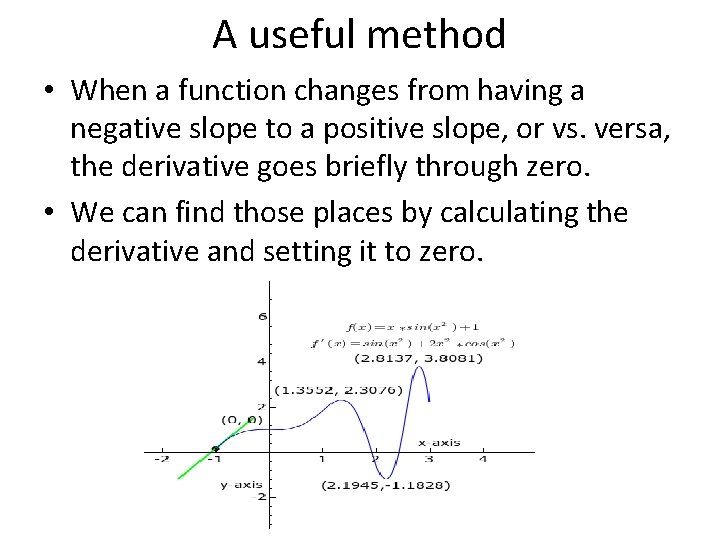
A useful method • When a function changes from having a negative slope to a positive slope, or vs. versa, the derivative goes briefly through zero. • We can find those places by calculating the derivative and setting it to zero.

Getting useful numbers • Suppose y = x 2. • (a) Find the minimum If y = x 2 then dy/dx = 2 x 1 = 2 x. Set this equal to zero 2 x=0 so x=0 y = x 2 so if x = 0 then y = 0 Therefore the curve has zero slope at (0, 0)

Getting useful numbers • Suppose y = x 2. • TODO: Find (a) the location of the minimum, and (b) the slope at x=3 (a) See previous page (b) dy/dx = 2 x , so set x=3 then the slope is 2 x = 2. 3 = 6

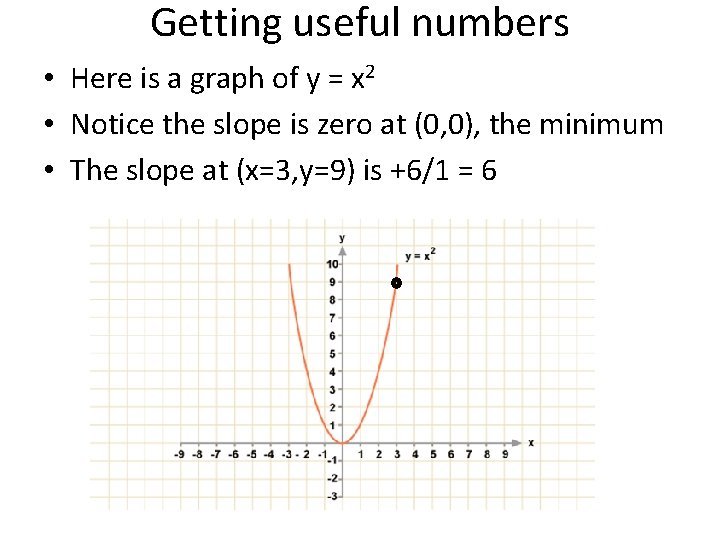
Getting useful numbers • Here is a graph of y = x 2 • Notice the slope is zero at (0, 0), the minimum • The slope at (x=3, y=9) is +6/1 = 6
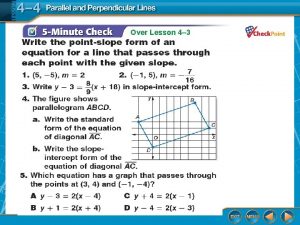
 Parallel lines have the same slope
Parallel lines have the same slope Slopes of parallel and perpendicular lines
Slopes of parallel and perpendicular lines Slopes of parallel and perpendicular lines assignment
Slopes of parallel and perpendicular lines assignment Lesson 12-4 slopes of parallel and perpendicular lines
Lesson 12-4 slopes of parallel and perpendicular lines Slopes of parallel and perpendicular lines lesson 8-1
Slopes of parallel and perpendicular lines lesson 8-1 If line a contains q(5 1)
If line a contains q(5 1) What slope is perpendicular to 5/8
What slope is perpendicular to 5/8 Find and use slopes of lines
Find and use slopes of lines Answers to how often
Answers to how often Page replacement algorithm online calculator
Page replacement algorithm online calculator Past repeated or habitual actions
Past repeated or habitual actions Rarely sometimes often
Rarely sometimes often The crucible final test
The crucible final test Laurie kirkland
Laurie kirkland Restate and paraphrase
Restate and paraphrase Hipaa frequently asked questions
Hipaa frequently asked questions Types of slopes
Types of slopes Oversteepened
Oversteepened The slope of parallel lines are always
The slope of parallel lines are always Parallel vs perpendicular
Parallel vs perpendicular The emigree poem structure
The emigree poem structure Two lines are parallel if their slopes are
Two lines are parallel if their slopes are Lesson 3-3 slopes of lines
Lesson 3-3 slopes of lines 3-5 slopes of lines
3-5 slopes of lines If line a contains q(5 1)
If line a contains q(5 1) Poem tissue
Poem tissue Slope review classifying slope
Slope review classifying slope Zero slop
Zero slop Slopes
Slopes Undefined slope
Undefined slope How to find the y intercept in an equation
How to find the y intercept in an equation Simple slopes analysis spss
Simple slopes analysis spss The graceful slopes glow even clearer
The graceful slopes glow even clearer Skradden slopes vista
Skradden slopes vista