3 5 Slopes of Lines Warm Up Find
















- Slides: 22

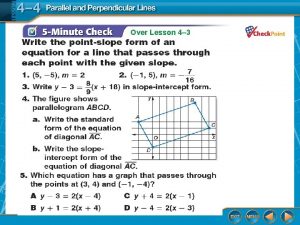
3 -5 Slopes of Lines Warm Up Find the value of m. 1. 2. 3. 4. undefined Holt Mc. Dougal Geometry 0

3 -5 Slopes of Lines Section 3 -5, Slopes of lines Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Learning Targets I will determine the slope of a line. I will use the slopes of lines to identify parallel and perpendicular lines. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Vocabulary rise run slope of a line zero slope undefined slope Holt Mc. Dougal Geometry

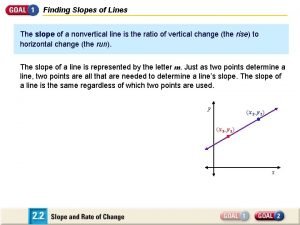
3 -5 Slopes of Lines The slope of a line in a coordinate plane is a number that describes the steepness of the line. Any two points on a line can be used to determine the slope. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Holt Mc. Dougal Geometry

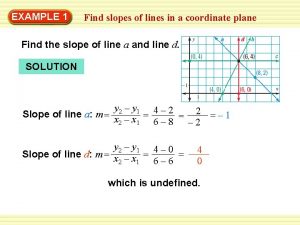
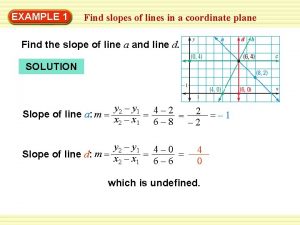
3 -5 Slopes of Lines Example 1 A: Finding the Slope of a Line Use the slope formula to determine the slope of each line. AB Substitute (– 2, 7) for (x 1, y 1) and (3, 7) for (x 2, y 2) in the slope formula and then simplify. This line has ZERO slope, not no slope. Holt Mc. Dougal Geometry

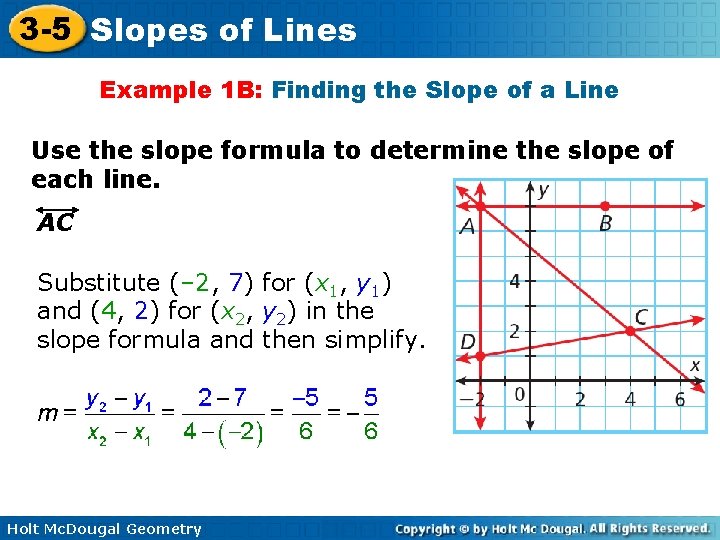
3 -5 Slopes of Lines Example 1 B: Finding the Slope of a Line Use the slope formula to determine the slope of each line. AC Substitute (– 2, 7) for (x 1, y 1) and (4, 2) for (x 2, y 2) in the slope formula and then simplify. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Example 1 C: Finding the Slope of a Line Use the slope formula to determine the slope of each line. AD Substitute (– 2, 7) for (x 1, y 1) and (– 2, 1) for (x 2, y 2) in the slope formula and then simplify. The slope is undefined. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Example 1 D: Finding the Slope of a Line Use the slope formula to determine the slope of each line. CD Substitute (4, 2) for (x 1, y 1) and (– 2, 1) for (x 2, y 2) in the slope formula and then simplify. Holt Mc. Dougal Geometry

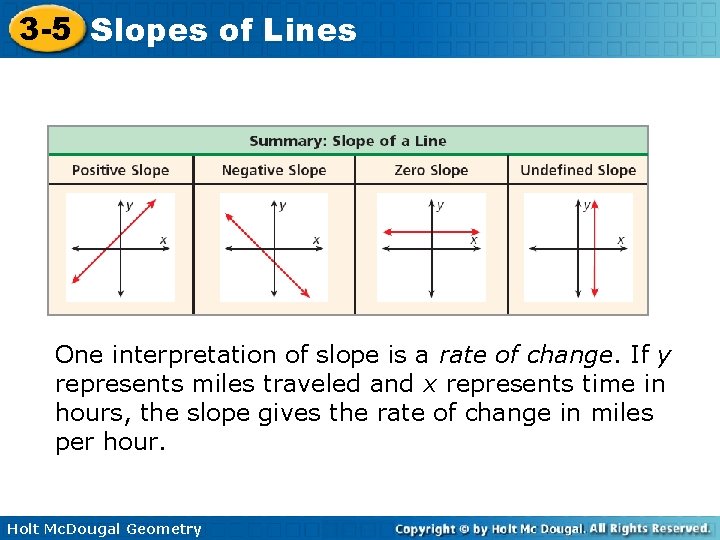
3 -5 Slopes of Lines One interpretation of slope is a rate of change. If y represents miles traveled and x represents time in hours, the slope gives the rate of change in miles per hour. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Holt Mc. Dougal Geometry

3 -5 Slopes of Lines If a line has a slope of perpendicular line is The ratios If you multiply Holt Mc. Dougal Geometry and , then the slope of a. are called opposite reciprocals. your product is -1.

3 -5 Slopes of Lines Caution! Four given points do not always determine two lines. Graph the lines to make sure the points are not collinear. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Example 2 A: Determining Whether Lines Are Parallel, Perpendicular, or Neither Graph each pair of lines. Use their slopes to determine whether they are parallel, perpendicular, or neither. UV and XY for U(0, 2), V(– 1, – 1), X(3, 1), and Y(– 3, 3) The products of the slopes is – 1, so the lines are perpendicular. Holt Mc. Dougal Geometry

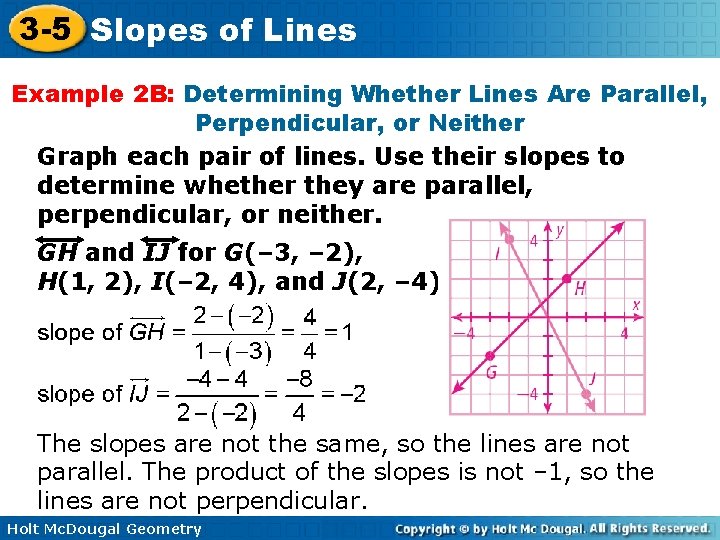
3 -5 Slopes of Lines Example 2 B: Determining Whether Lines Are Parallel, Perpendicular, or Neither Graph each pair of lines. Use their slopes to determine whether they are parallel, perpendicular, or neither. GH and IJ for G(– 3, – 2), H(1, 2), I(– 2, 4), and J(2, – 4) The slopes are not the same, so the lines are not parallel. The product of the slopes is not – 1, so the lines are not perpendicular. Holt Mc. Dougal Geometry

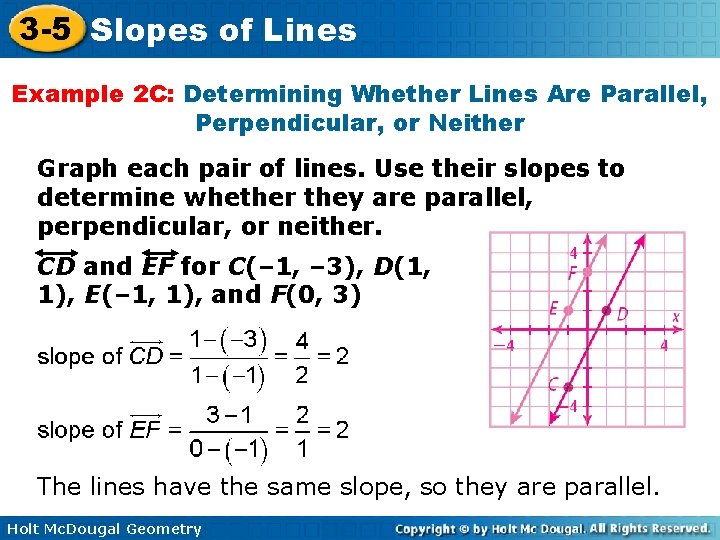
3 -5 Slopes of Lines Example 2 C: Determining Whether Lines Are Parallel, Perpendicular, or Neither Graph each pair of lines. Use their slopes to determine whether they are parallel, perpendicular, or neither. CD and EF for C(– 1, – 3), D(1, 1), E(– 1, 1), and F(0, 3) The lines have the same slope, so they are parallel. Holt Mc. Dougal Geometry

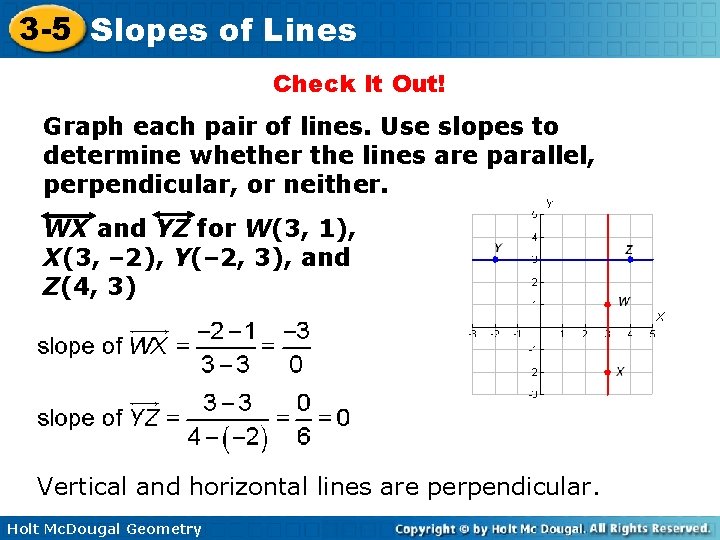
3 -5 Slopes of Lines Check It Out! Graph each pair of lines. Use slopes to determine whether the lines are parallel, perpendicular, or neither. WX and YZ for W(3, 1), X(3, – 2), Y(– 2, 3), and Z(4, 3) Vertical and horizontal lines are perpendicular. Holt Mc. Dougal Geometry

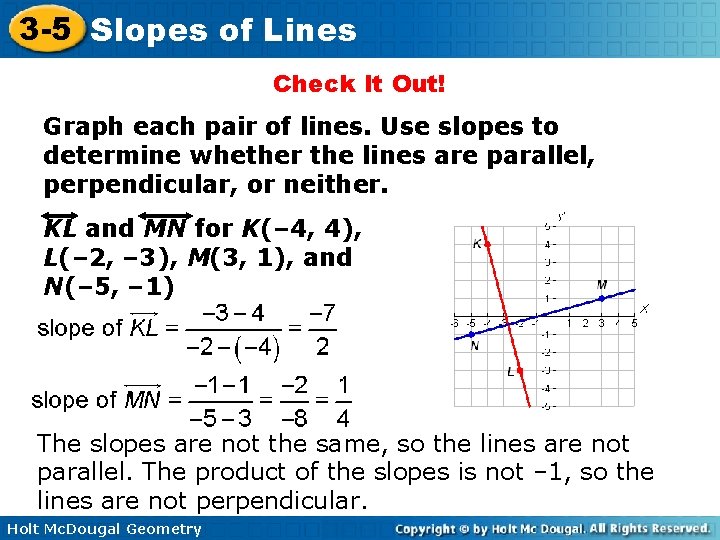
3 -5 Slopes of Lines Check It Out! Graph each pair of lines. Use slopes to determine whether the lines are parallel, perpendicular, or neither. KL and MN for K(– 4, 4), L(– 2, – 3), M(3, 1), and N(– 5, – 1) The slopes are not the same, so the lines are not parallel. The product of the slopes is not – 1, so the lines are not perpendicular. Holt Mc. Dougal Geometry

3 -5 Slopes of Lines CRITICAL THINKING: If the slope of a line is greater than 0 but less than 1, what inequality can use to find the slope (m) of a line perpendicular to the given line? Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Homework, Pg 186, #10 - 22 Holt Mc. Dougal Geometry

3 -5 Slopes of Lines Lesson Quiz 1. Use the slope formula to determine the slope of the line that passes through M(3, 7) and N(– 3, 1). m=1 Graph each pair of lines. Use slopes to determine whether they are parallel, perpendicular, or neither. 2. AB and XY for A(– 2, 5), B(– 3, 1), X(0, – 2), and Y(1, 2) 4, 4; parallel 3. MN and ST for M(0, – 2), N(4, – 4), S(4, 1), and T(1, – 5) Holt Mc. Dougal Geometry
 Find and use slopes of lines
Find and use slopes of lines Parallel lines slope
Parallel lines slope Parallel and perpendicular lines worksheet doc
Parallel and perpendicular lines worksheet doc Slopes of parallel and perpendicular lines assignment
Slopes of parallel and perpendicular lines assignment The slope of parallel lines are always
The slope of parallel lines are always Two lines are parallel if their slopes are
Two lines are parallel if their slopes are 3-3 slopes of lines answer key
3-3 slopes of lines answer key 8-1 slopes of parallel and perpendicular lines
8-1 slopes of parallel and perpendicular lines Homework 5 slopes of lines
Homework 5 slopes of lines 3-3 slope of lines
3-3 slope of lines 3 sets of parallel lines
3 sets of parallel lines Slopes of parallel and perpendicular lines lesson 8-1
Slopes of parallel and perpendicular lines lesson 8-1 If line a contains q(5 1)
If line a contains q(5 1) Slope review classifying slope
Slope review classifying slope Warm line meaning
Warm line meaning Angles & lines unit warm ups
Angles & lines unit warm ups Quiz 3-1 parallel lines transversals and angles
Quiz 3-1 parallel lines transversals and angles Slope types
Slope types Geology
Geology Perpendicular slopes examples
Perpendicular slopes examples The emigree by carol rumens
The emigree by carol rumens Living space poem
Living space poem Zero slop
Zero slop