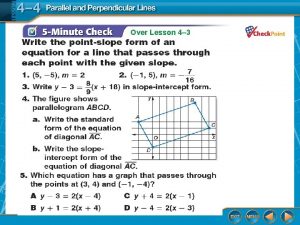
Slopes and Areas Frequently we will want to

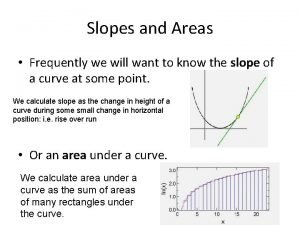
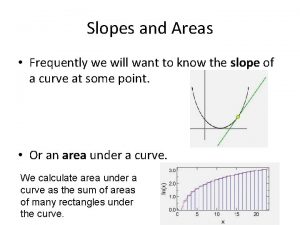
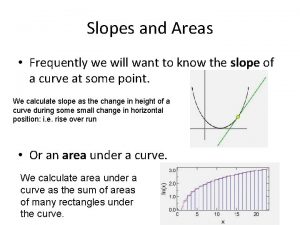
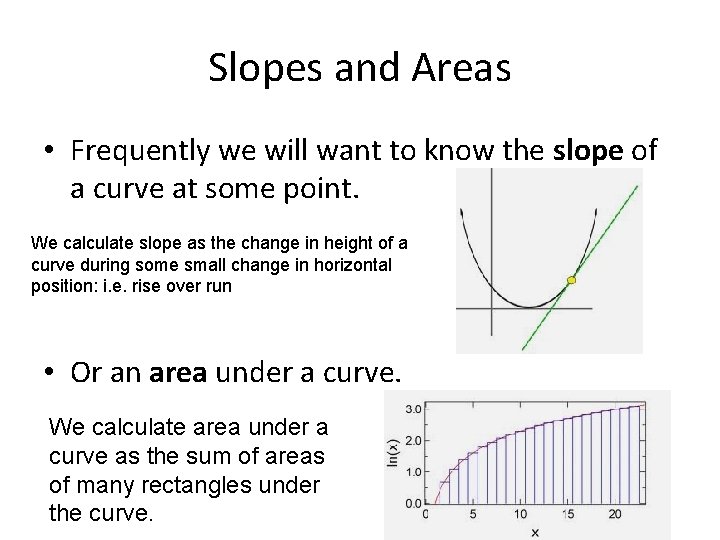
Slopes and Areas • Frequently we will want to know the slope of a curve at some point. We calculate slope as the change in height of a curve during some small change in horizontal position: i. e. rise over run • Or an area under a curve. We calculate area under a curve as the sum of areas of many rectangles under the curve.

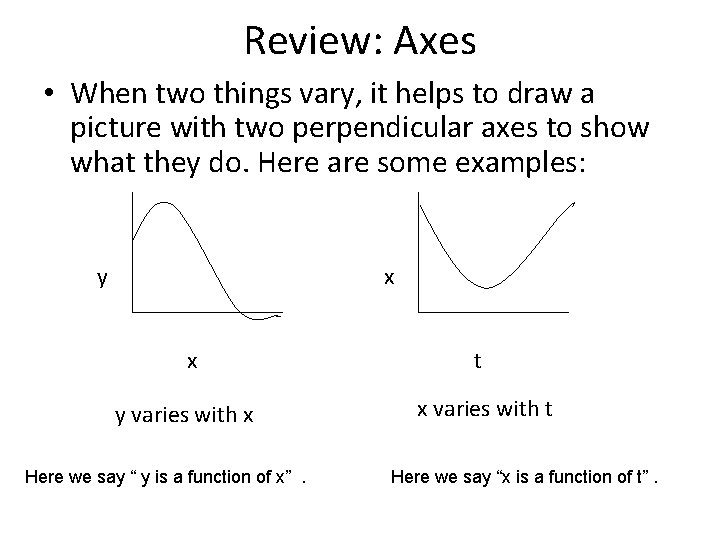
Review: Axes • When two things vary, it helps to draw a picture with two perpendicular axes to show what they do. Here are some examples: y x x y varies with x Here we say “ y is a function of x”. t x varies with t Here we say “x is a function of t”.

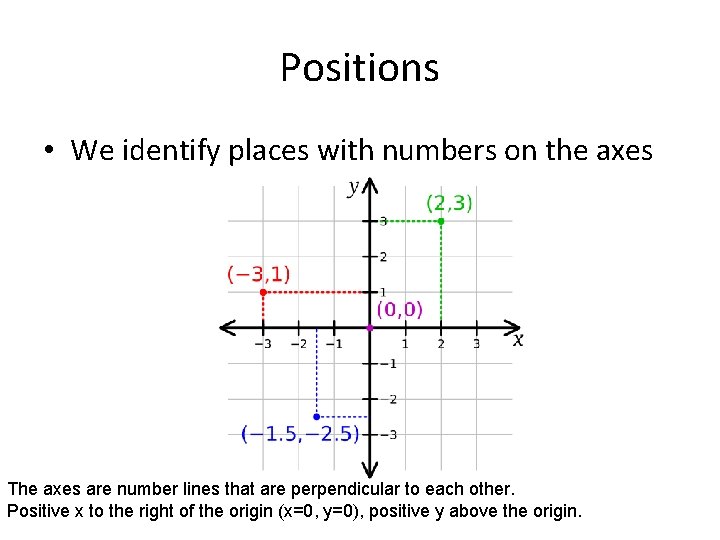
Positions • We identify places with numbers on the axes The axes are number lines that are perpendicular to each other. Positive x to the right of the origin (x=0, y=0), positive y above the origin.

Straight Lines • Sometimes we can write an equation for how one variable varies with the other. For example a straight line can be described as y = ax + b Here, y is a position on the line along the y-axis, x is a position on the line along the xaxis, a is the slope, and b is the place where the line hits the y-axis

Straight Line Slope y = ax + b The slope, a, is just the rise Dy divided by the run Dx. We can do this anywhere on the line. Proceed in the positive x direction for some number of units, and count the number of units up or down the y changes So the slope of the line here is Dy = -3 2 Dx Remember: Rise over Run and up and right are positive

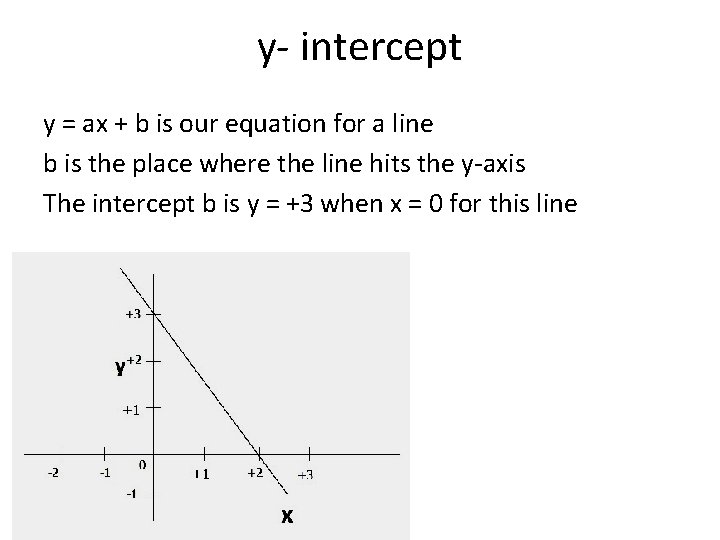
y- intercept y = ax + b is our equation for a line b is the place where the line hits the y-axis The intercept b is y = +3 when x = 0 for this line

y = ax + b is the general equation for a line We want an equation for this line Equation of our example line So the equation of the line here is y = -3 x + 3 2 We plugged in the slope and y intercept

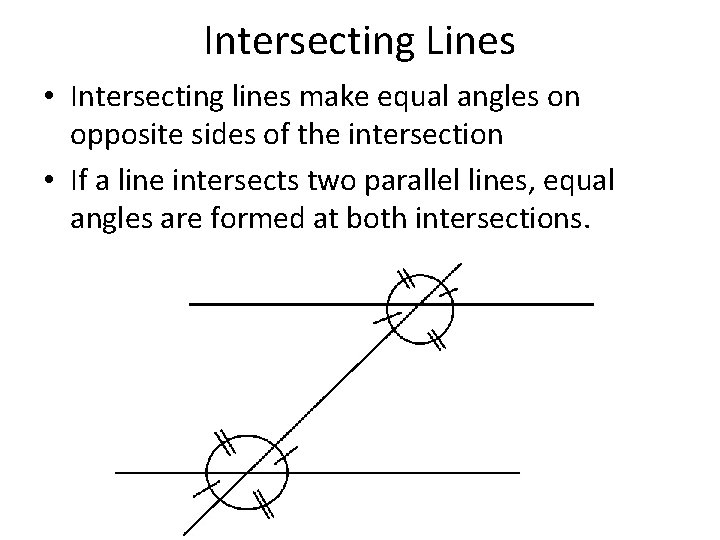
Intersecting Lines • Intersecting lines make equal angles on opposite sides of the intersection • If a line intersects two parallel lines, equal angles are formed at both intersections.

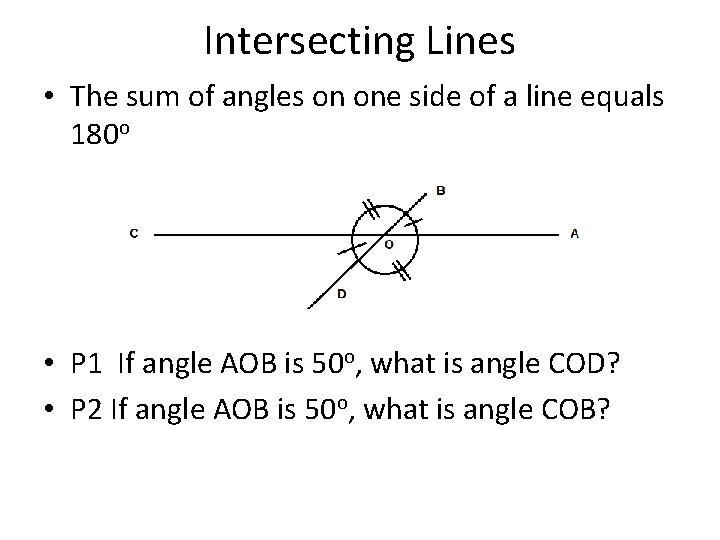
Intersecting Lines • The sum of angles on one side of a line equals 180 o • P 1 If angle AOB is 50 o, what is angle COD? • P 2 If angle AOB is 50 o, what is angle COB?

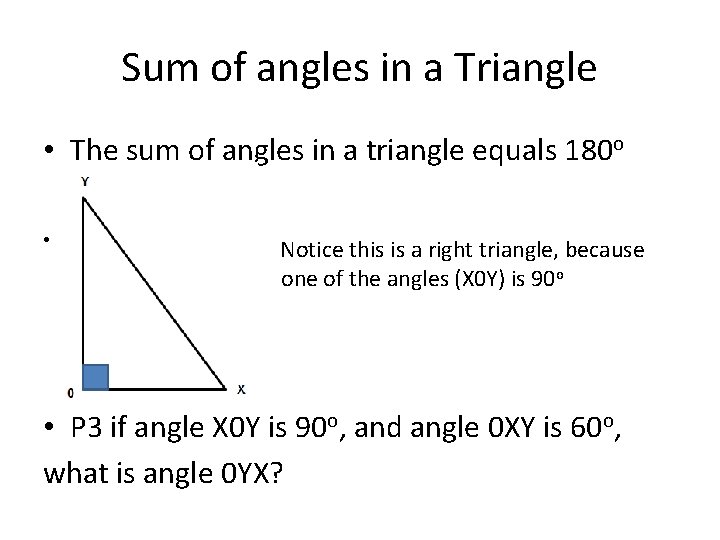
Sum of angles in a Triangle • The sum of angles in a triangle equals 180 o • Notice this is a right triangle, because one of the angles (X 0 Y) is 90 o • P 3 if angle X 0 Y is 90 o, and angle 0 XY is 60 o, what is angle 0 YX?

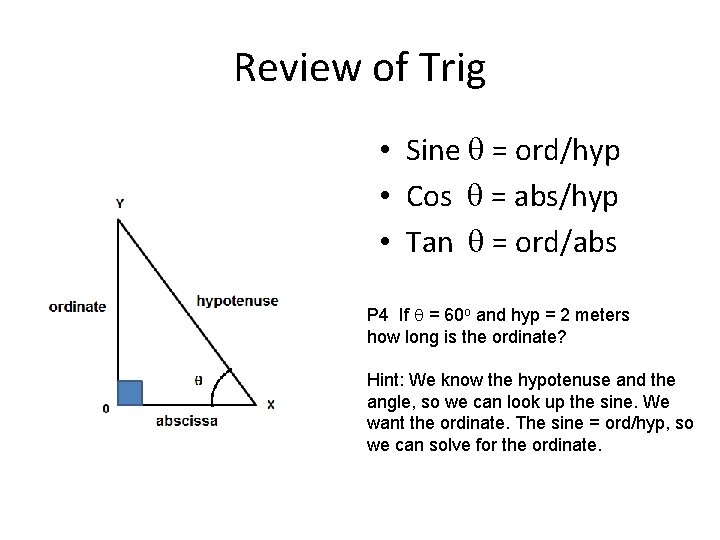
Review of Trig • Sine q = ord/hyp • Cos q = abs/hyp • Tan q = ord/abs P 4 If q = 60 o and hyp = 2 meters how long is the ordinate? Hint: We know the hypotenuse and the angle, so we can look up the sine. We want the ordinate. The sine = ord/hyp, so we can solve for the ordinate.

Review of Trig • Sine q = ord/hyp (1) • Cos q = abs/hyp (2) • Tan q = ord/abs (3) P 4 If q = 60 o and hyp = 2 meters how long is the ordinate? Soln: Sine 60 o = 0. 866 Solve Eqn (1) for ordinate = Sine q * hypotenuse Plug in: ordinate = 0. 866 * 2 meters ordinate = 1. 732 meters Hint: We know the hypotenuse and the angle, so we can look up the sine. We want the ordinate. The sine = ord/hyp, so we can solve for the ordinate.