l SecantLine Slopes to TangentLine Slopes 2 7

Wednesday, Monday, February 1, 2016 6, 2019 MAT 145

We call this slope calculation the derivative of f at x = a. Wednesday,

• • The value f ’(a) is called: the derivative of f at

Can we create a derivative function f that will be true for any x

Calculate the derivative function, f ’(x), for f(x) = x 2. Use the limit

Find an equation of the tangent line to the parabola y = x 2

The derivative in action! S(t) represents the distance traveled by some object, where t

The derivative in action! C(p) represents the total daily cost of operating a hospital,

The derivative in action! V(r) represents the volume of a sphere, where r is

Here is a graph of the function y = g(x). Arrange the following values

Here is the graph of the function y = |x|. Why does the derivative

Three situations for which a derivative DOES NOT EXIST! Wednesday, February 6, 2019 MAT

For each graphed function, state points at which the function is NOT differentiable. Explain

Match each function, a-d, with its derivative, I-IV. Wednesday, February 6, 2019 MAT 145

Here are the graphs of four functions. One represents the position of a car

Here is the graph of a function f. Use it to sketch the graph

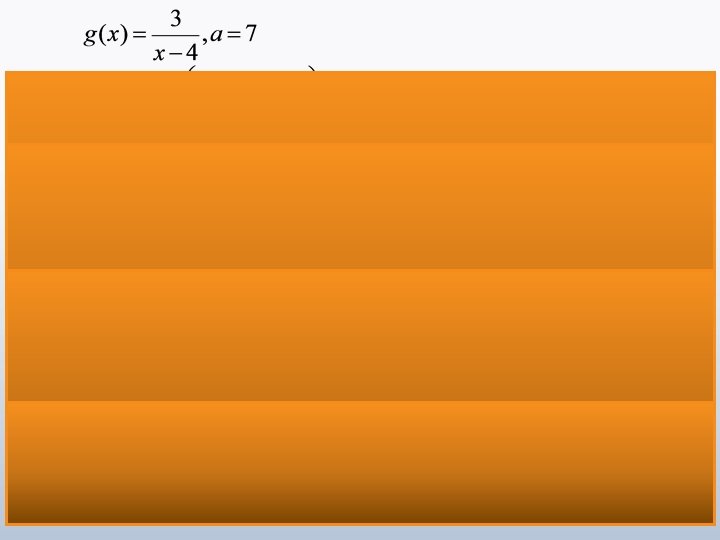
Slides: 25

Download presentation

l Secant-Line Slopes to Tangent-Line Slopes (2. 7 & 2. 8) Using limits to determine exact values for tangent-line slope l This limit statement for tangent-line slope is called the derivative of th function l l. Test #1: Friday, STV 308 Wednesday, February 6, 2019 MAT 145

Wednesday, February 6, 2019 MAT 145

Wednesday, Monday, February 1, 2016 6, 2019 MAT 145

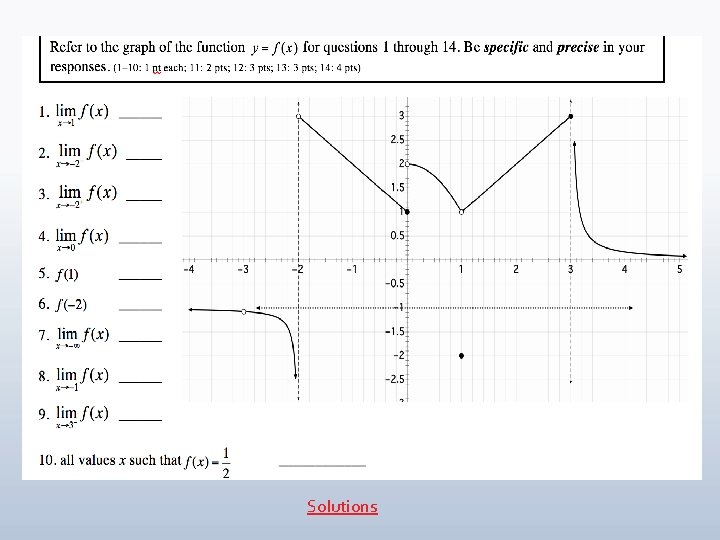
Solutions

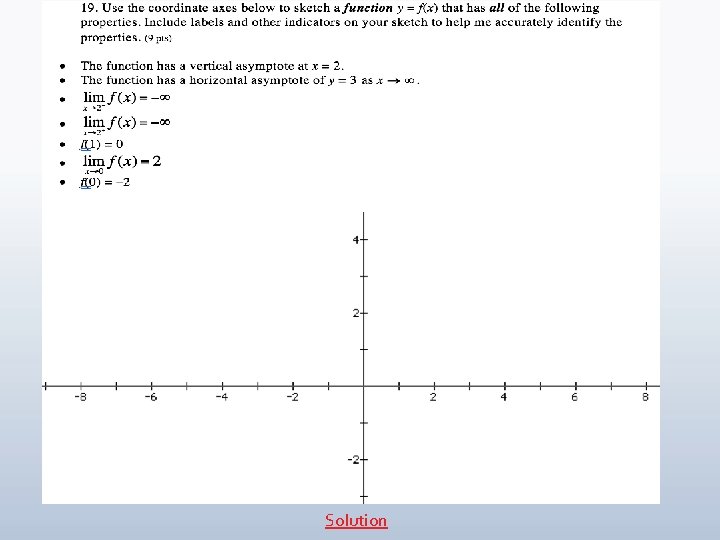
Solution

We call this slope calculation the derivative of f at x = a. Wednesday, February 6, 2019 MAT 145

• • The value f ’(a) is called: the derivative of f at x = a, the instantaneous rate of change of f at x = a, the slope of f at x = a, and the slope of the tangent line to f at x = a. Wednesday, February 6, 2019 MAT 145

Can we create a derivative function f that will be true for any x value where a derivative exists? Wednesday, February 6, 2019 MAT 145

Calculate the derivative function, f ’(x), for f(x) = x 2. Use the limit definition of the derivative. Wednesday, February 6, 2019 MAT 145

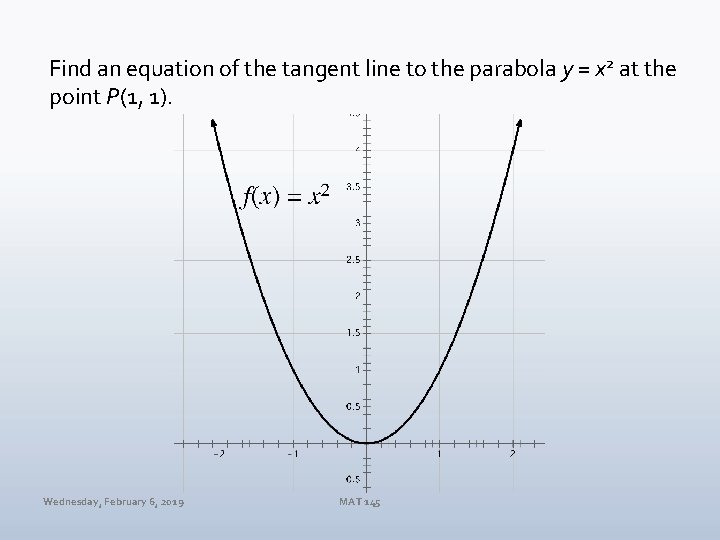
Find an equation of the tangent line to the parabola y = x 2 at the point P(1, 1). Wednesday, February 6, 2019 MAT 145

Wednesday, February 6, 2019 MAT 145

The derivative in action! S(t) represents the distance traveled by some object, where t is in minutes and S is in feet. What is the meaning of S’(12)=100? Wednesday, February 6, 2019 MAT 145

The derivative in action! S(t) represents the distance traveled by some object, where t is in minutes and S is in feet. What is the meaning of S’(12)=100? • From the description of the context, the “rate units” are: feet per minute. • The value 12 is an input variable, so we are looking at the precise instant that 12 minutes of travel has occurred, since some designated starting time when t = 0. • S’ indicates rate of change of S, indicating we have information about how S is changing with respect to t, in feet per minute. • The value 100 specifies the rate: 100 feet per minute. Putting it all together: • At precisely 12 minutes into the trip, the object’s position is increasing at the rate of 100 feet per minute. Wednesday, February 6, 2019 MAT 145

The derivative in action! C(p) represents the total daily cost of operating a hospital, where p is the number of patients and C is in thousands of dollars. What is the meaning of C’(90)=4. 5? • From the description of the context, the “rate units” are: thousands of dollars per patient. • The value 90 is an input variable, so we are looking at the precise instant when 90 patients are in the hospital. • C’ indicates rate of change of C, indicating we have information about how C is changing with respect to p, in thousands of dollars per patient. • The value 4. 5 specifies the rate: 4. 5 thousand dollars ($4500) per patient. Putting it all together: • At precisely the instant that 90 patients are in the hospital, the cost per patient is increasing at the rate of $4500 per patient. Wednesday, February 6, 2019 MAT 145

The derivative in action! V(r) represents the volume of a sphere, where r is the radius of the sphere in cm. What is the meaning of V ’(3)=36π? • From the description of the context, the “rate units” are: cubic cm of volume per cm of radius. • The value 3 is an input variable, so we are looking at the precise instant when the sphere’s radius is 3 cm long. • V’ indicates rate of change of V, indicating we have information about how V is changing with respect to r, in cubic cm per cm. • The value 36π specifies the rate: 36π cubic cm of volume per 1 cm of radius length. Putting it all together: • At precisely the instant that the sphere has a radius length of 3 cm, the sphere’s volume is increasing at the rate of 36π cubic cm per cm of radius length. Wednesday, February 6, 2019 MAT 145

Wednesday, February 6, 2019 MAT 145

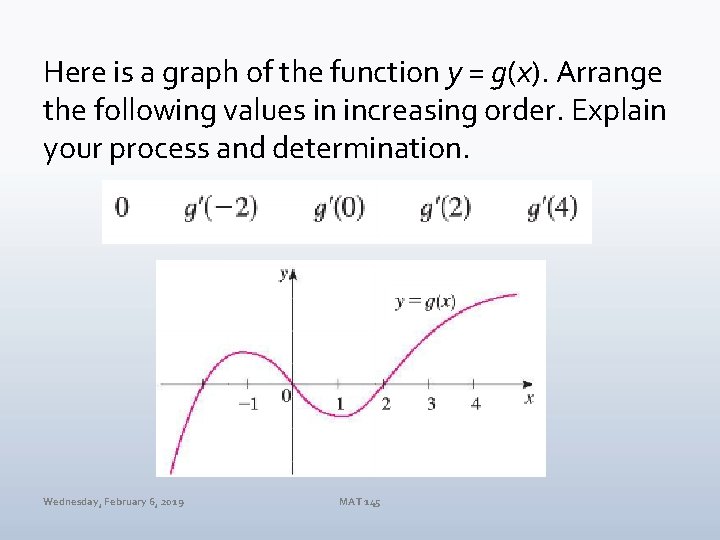
Here is a graph of the function y = g(x). Arrange the following values in increasing order. Explain your process and determination. Wednesday, February 6, 2019 MAT 145

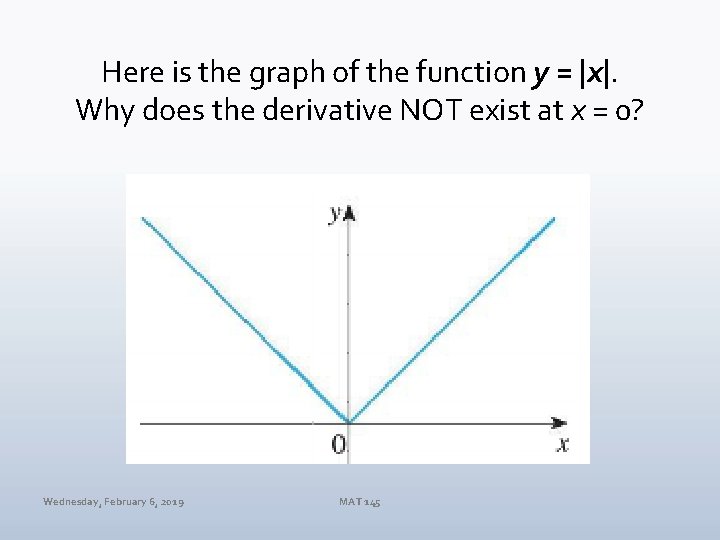
Here is the graph of the function y = |x|. Why does the derivative NOT exist at x = 0? Wednesday, February 6, 2019 MAT 145

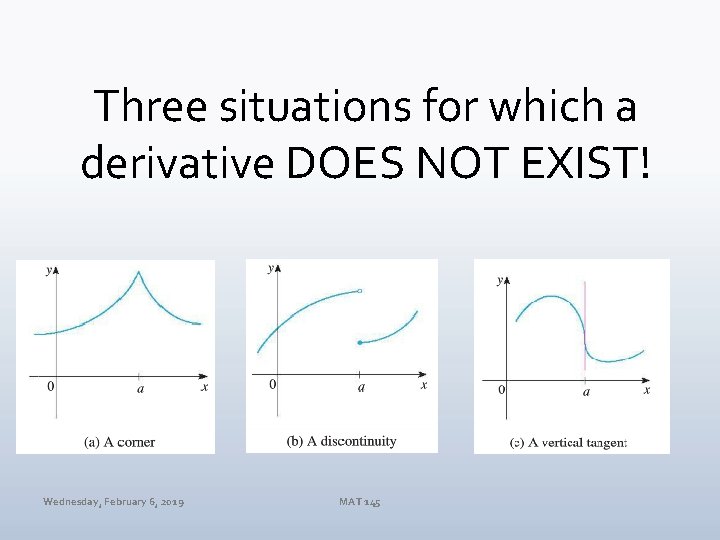
Three situations for which a derivative DOES NOT EXIST! Wednesday, February 6, 2019 MAT 145

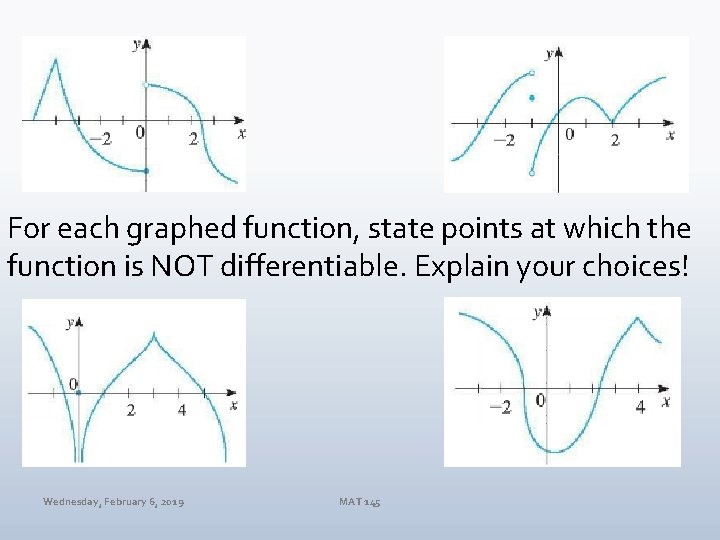
For each graphed function, state points at which the function is NOT differentiable. Explain your choices! Wednesday, February 6, 2019 MAT 145

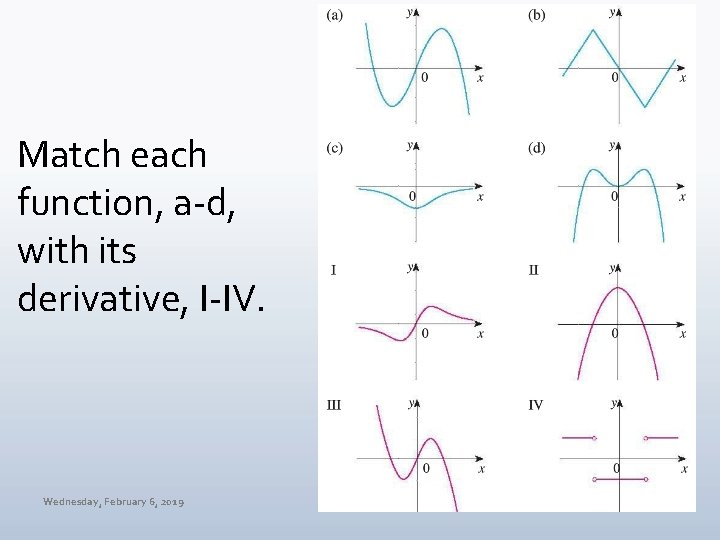
Match each function, a-d, with its derivative, I-IV. Wednesday, February 6, 2019 MAT 145

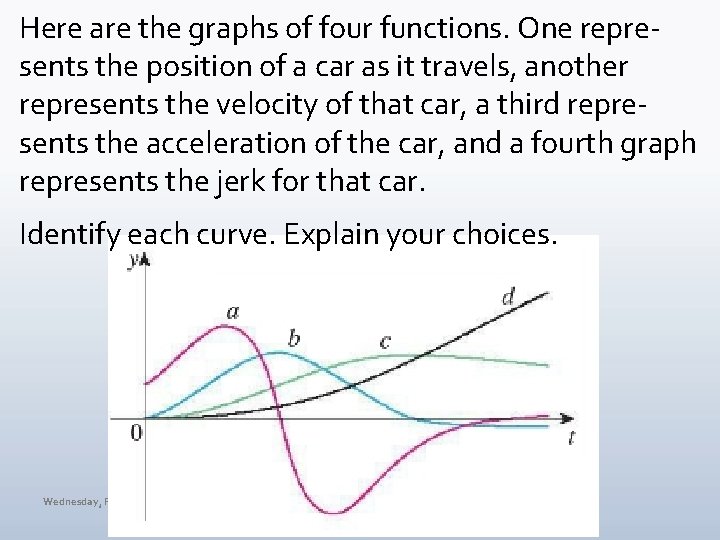
Here are the graphs of four functions. One represents the position of a car as it travels, another represents the velocity of that car, a third represents the acceleration of the car, and a fourth graph represents the jerk for that car. Identify each curve. Explain your choices. Wednesday, February 6, 2019 MAT 145

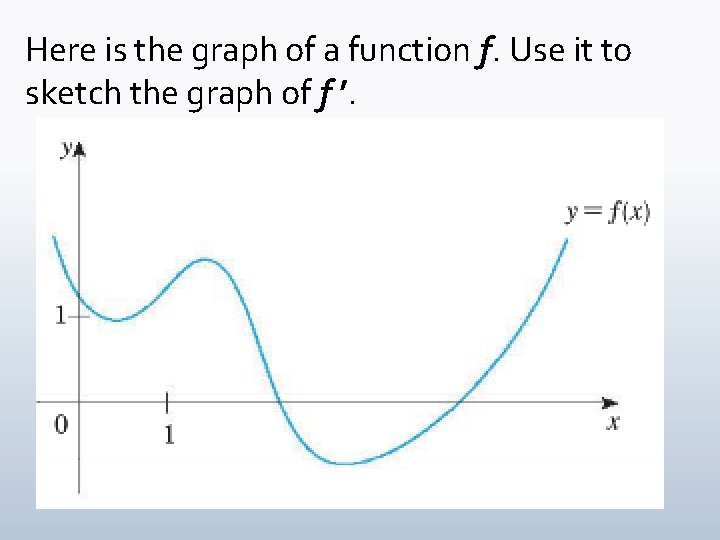
Here is the graph of a function f. Use it to sketch the graph of f ’. Wednesday, February 6, 2019 MAT 145