Linear Functions and Slopes Objectives Find the slopes

Linear Functions and Slopes Objectives • Find the slopes of lines • Write and graph linear equations • Model data with linear functions and make predictions

VOCABULARY Linear equation Slope Point-slope form Slope-intercept form
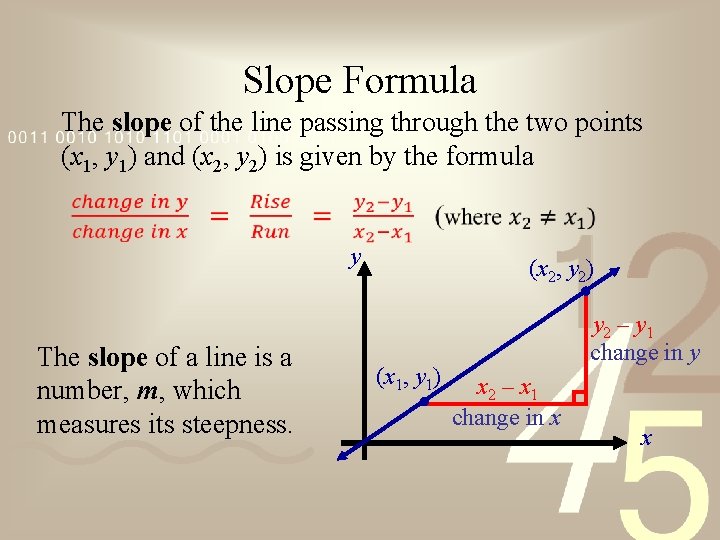
Slope Formula The slope of the line passing through the two points (x 1, y 1) and (x 2, y 2) is given by the formula y The slope of a line is a number, m, which measures its steepness. (x 2, y 2) (x 1, y 1) y 2 – y 1 change in y x 2 – x 1 change in x x
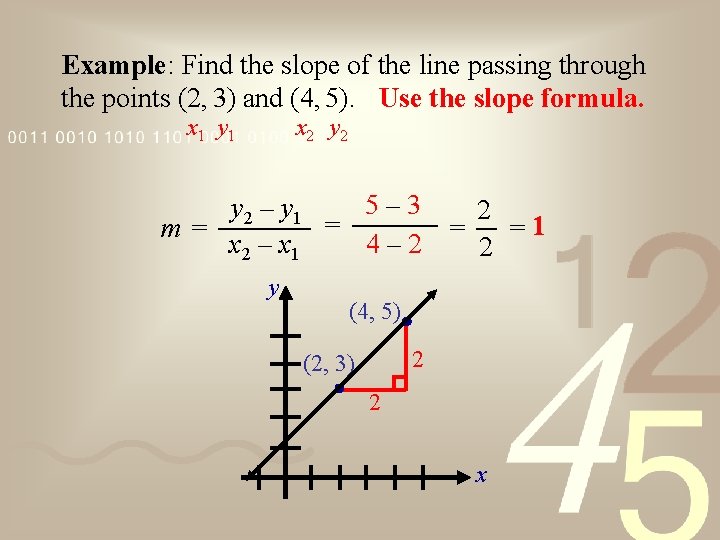
Example: Find the slope of the line passing through the points (2, 3) and (4, 5). Use the slope formula. x 2 y 2 x 1 y 1 5– 3 y 2 – y 1 2 = m= = =1 4– 2 x 2 – x 1 2 y (4, 5) 2 (2, 3) 2 x

Your Turn •
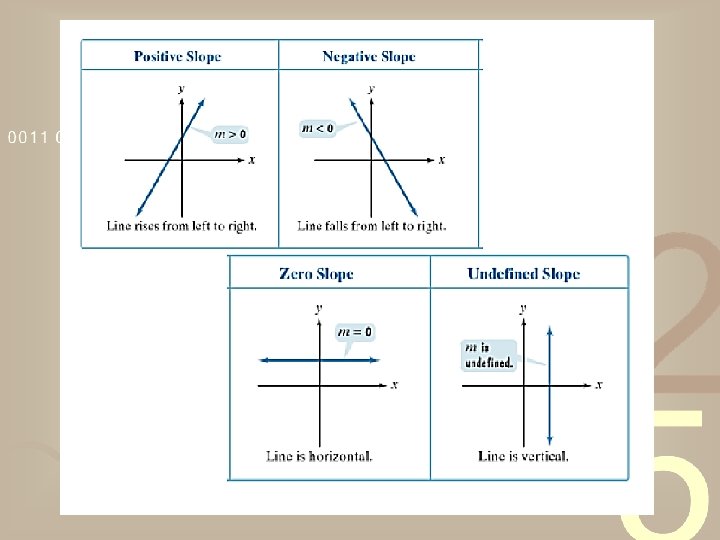

Slope of Horizontal Lines • Slope of a horizontal line is 0 • Equation of a horizontal line that passes through the point (a, b):

Slope of Vertical Lines • Slope of a vertical line is undefined • Equation of a vertical line that passes through the point (a, b):
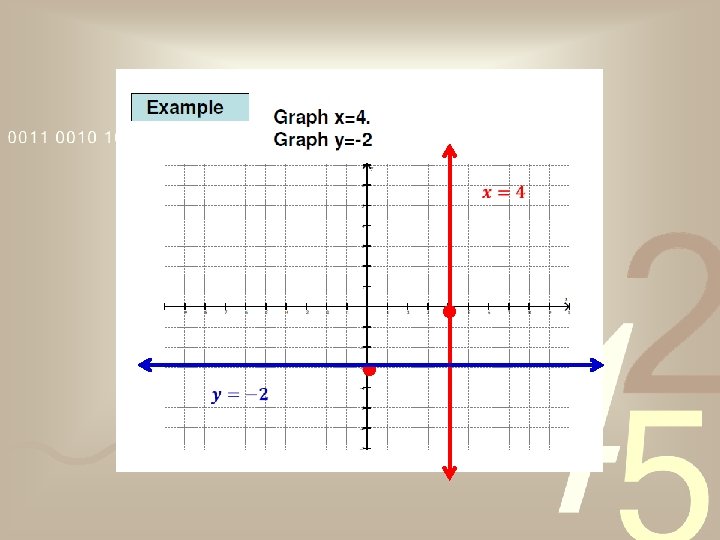

Because the slope of line is constant, it is possible to use any point on a line and the slope of the line to write an equation of the line in point-slope form. All you need is a point and the slope.

Point-Slope Form The Point-Slope form is derived from the slope formula. Slope Formula Change y 2, x 2 to just y and x. Multiple both sides by the denominator. Point-Slope Form

Point-Slope Form A linear equation written in the form y – y 1 = m(x – x 1) is in point-slope form. The graph of this equation is a line with slope m passing through the point (x 1, y 1). y Example: 8 The graph of the equation 4 y – 3 = - 1 (x – 4) is a line m=- 1 2 (4, 3) 2 of slope m = - 1 passing 2 through the point (4, 3). x 4 8

Use the point-slope form of the equation.

Rule # 1: We need to find the slope, whether it is given to us or it needs to be calculated. y 2 – y 1 m= x 2 – x 1 To be continued

The above answer is the slope-intercept form of the equation.

Slope-Intercept Form A linear equation written in the form y = mx + b is in slope-intercept form. The slope is m and the y-intercept is b. To graph an equation in slope-intercept form: 1. Write the equation in the form y = mx + b. Identify m and b. 2. Plot the y-intercept (0, b). 3. Starting at the y-intercept, find another point on the line using the slope. 4. Draw the line through (0, b) and the point located using the slope.

Example: Graph the line y = 2 x – 4. 1. The equation y = 2 x – 4 is in the slope-intercept form. So, m = 2 and b = - 4. y 2. Plot the y-intercept, (0, - 4). x 3. The slope is 2. m = change in y = 2 1 change in x 4. Start at the point (0, 4). Count 1 unit to the right and 2 units up to locate a second point on the line. The point (1, -2) is also on the line. 5. Draw the line through (0, 4) and (1, -2) 2 (0, - 4) 1
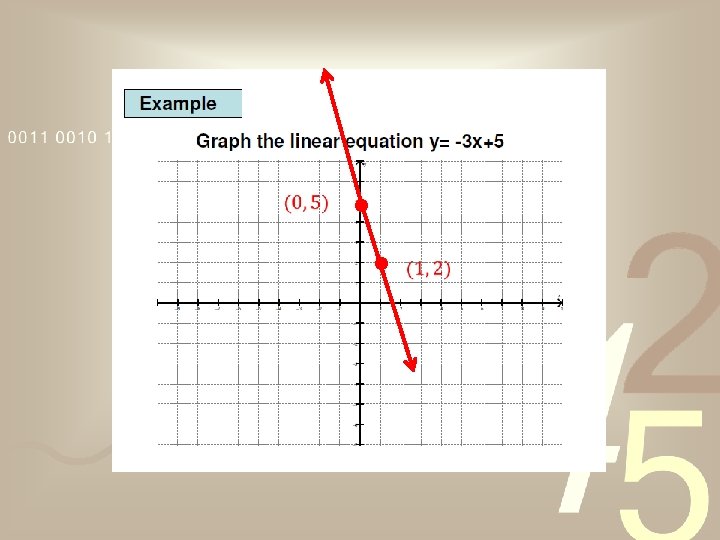
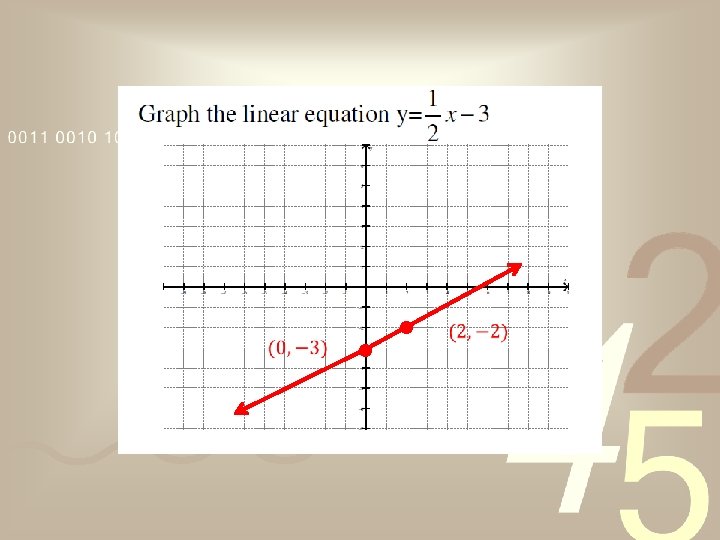

General Form of the Equation of a Line



Linear Equations The point (0, 4) is the y-intercept. The point (6, 0) is the x-intercept. y (0, 4) (6, 0) -2 2 x

Summary of Equations of Lines 1. 2. 3. 4. 5. General form: Vertical line: Horizontal line: Slope-intercept form: Point-slope form:

Linear Model Writing an equation of a line that models real data: If the data changes at a fairly constant rate, the rate of change is the slope. An initial condition would be the y-intercept. • Example: Suppose there is a flat rate of $. 20 plus a charge of $. 10/minute to make a phone call. Write an equation that gives the cost y for a call of x minutes. Note: The initial condition is the flat rate of $. 20 and the rate of change is $. 10/minute. Solution: y =. 10 x +. 20

Linear Model Writing an equation of a line that models real data: If the data changes at a fairly constant rate, the rate of change is the slope. An initial condition would be the y-intercept. • Example: The percentage of mothers of children under 1 year old who participated in the US labor force is shown in the table. Find an equation that models the data. Using (1980, 38) and (1998, 59)

Your Turn The net sales for a car manufacturer were $14. 61 billion in 2005 and $15. 78 billion in 2006. Write a linear equation giving the net sales y in terms of x, where x is the number of years since 2000. Then use the equation to predict the net sales for 2007. Answer: y=1. 17 x+8. 76, predicted sales for 2007 is $16. 95 billion.

Summary of Linear Graphs

- Slides: 29