Finding Slopes of Lines The slope of a

Finding the Slope of a Line Find the slope of the line passing through

Classifying Lines Using Slope CONCEPT SUMMARY CLASSIFICATION OF LINES BY SLOPE A line with

Classifying Lines Using Slope Without graphing tell whether the line through the given points

Comparing Steepness of Lines The slope of a line tells you more than whether

Comparing Steepness of Lines Tell which line is steeper. Line 1: through (2, 3)

Classifying Parallel and Perpendicular Lines Slope can be used to determine whether two different

Classifying Parallel and Perpendicular Lines Tell whether the lines are parallel, perpendicular, or neither.

Using Slope in Real Life In a home repair manual the following ladder safety

Finding the Slope of a Line In real-life problems slope is often used to

Slides: 15

Download presentation

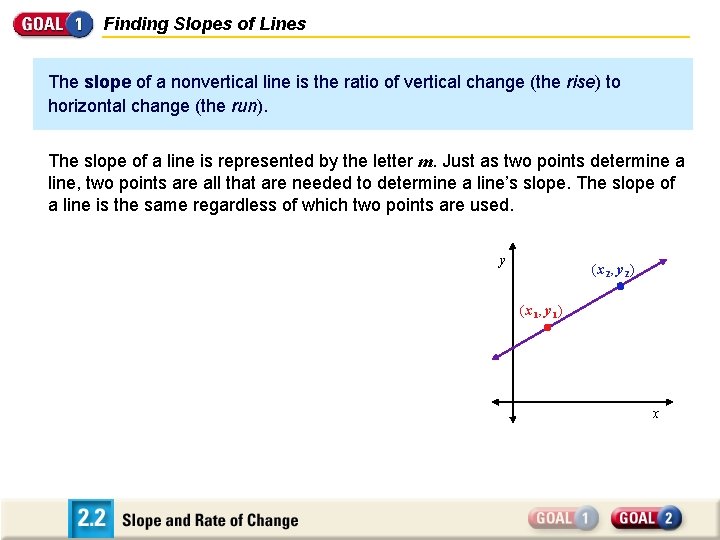
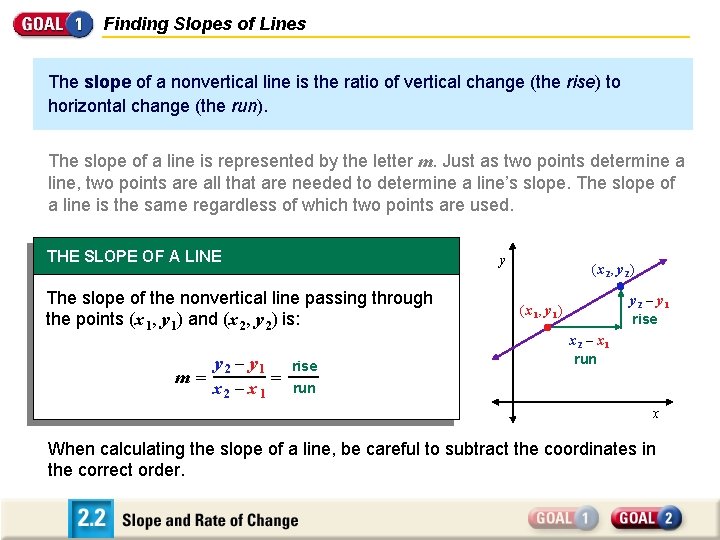
Finding Slopes of Lines The slope of a nonvertical line is the ratio of vertical change (the rise) to horizontal change (the run). The slope of a line is represented by the letter m. Just as two points determine a line, two points are all that are needed to determine a line’s slope. The slope of a line is the same regardless of which two points are used. THE SLOPE OF A LINE y The slope of the nonvertical line passing through the points (x 1, y 1) and (x 2, y 2) is: m = y 2 – y 1 = x 2 – x 1 rise (x 2, y 2) y 2 – y 1 rise (x 1, y 1) x 2 – x 1 run x When calculating the slope of a line, be careful to subtract the coordinates in the correct order.

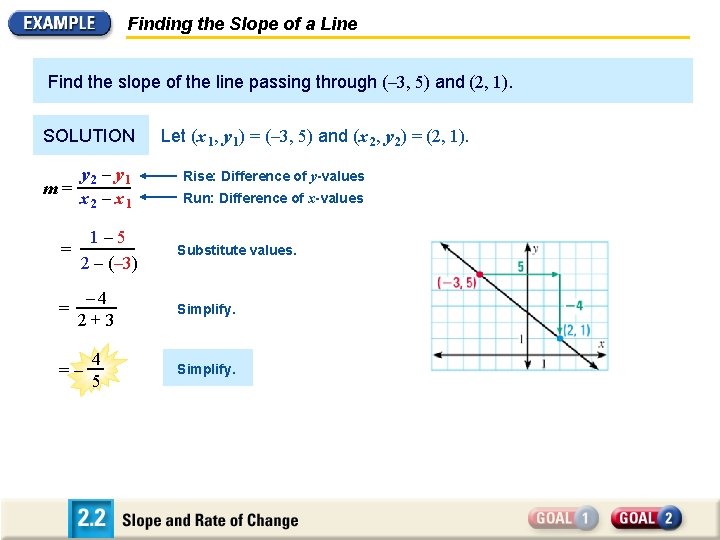
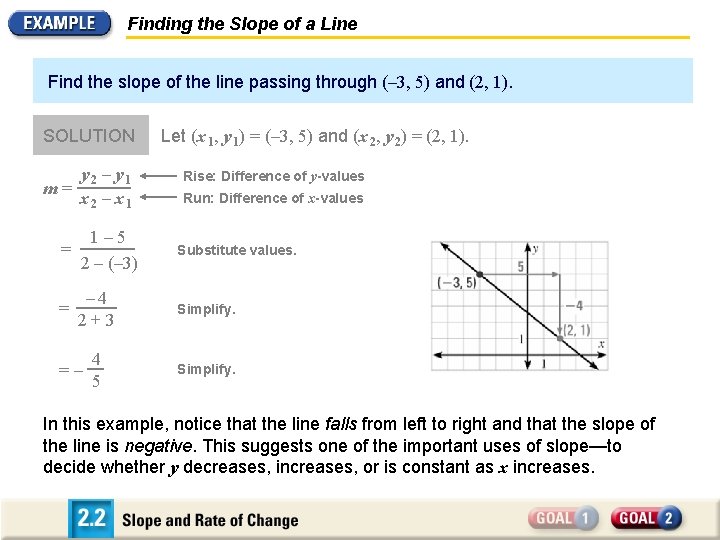
Finding the Slope of a Line Find the slope of the line passing through (– 3, 5) and (2, 1). SOLUTION y 2 – y 1 m = x 2 – x 1 Let (x 1, y 1) = (– 3, 5) and (x 2, y 2) = (2, 1). Rise: Difference of y-values Run: Difference of x-values = y 1 – 5 2 – y 1 x 2 – x 1 2 – (– 3) Substitute values. = – 4 2 + 3 Simplify. 4 5 Simplify. = – In this example, notice that the line falls from left to right and that the slope of the line is negative. This suggests one of the important uses of slope—to decide whether y decreases, increases, or is constant as x increases.

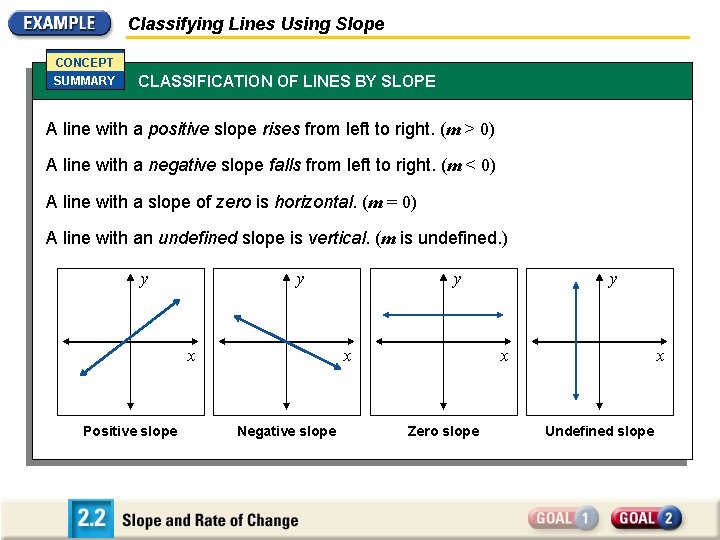
Classifying Lines Using Slope CONCEPT SUMMARY CLASSIFICATION OF LINES BY SLOPE A line with a positive slope rises from left to right. (m > 0) A line with a negative slope falls from left to right. (m < 0) A line with a slope of zero is horizontal. (m = 0) A line with an undefined slope is vertical. (m is undefined. ) y y x Positive slope y x Negative slope y x Zero slope x Undefined slope

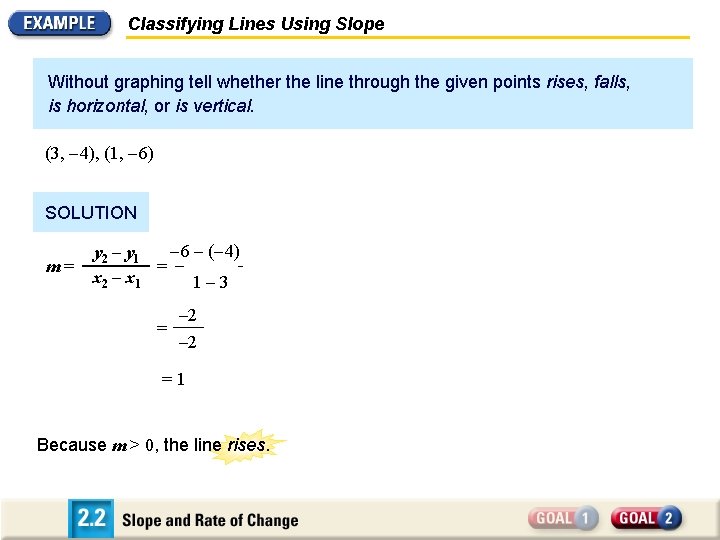
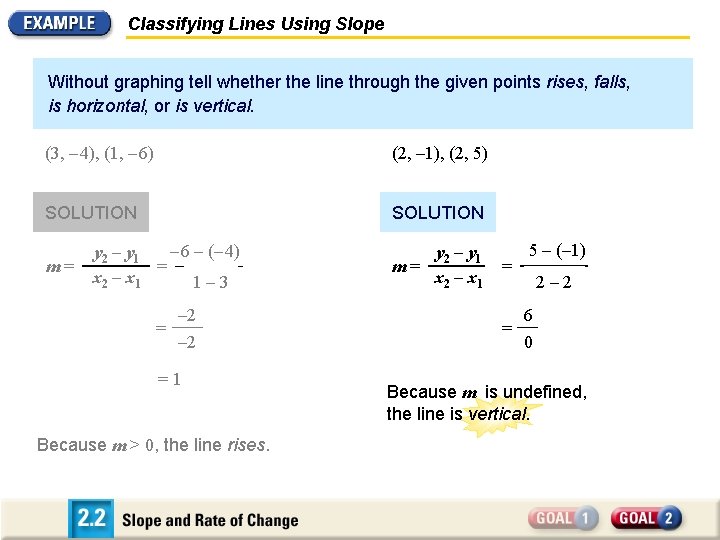
Classifying Lines Using Slope Without graphing tell whether the line through the given points rises, falls, is horizontal, or is vertical. (3, – 4), (1, – 6) SOLUTION m = – 6 – (– y 2 – y 1 y 2 – y 4) 1 = x 2 – x 1 – 3 2 – x 1 = – 2 = 1 Because m > 0, the line rises.

Classifying Lines Using Slope Without graphing tell whether the line through the given points rises, falls, is horizontal, or is vertical. (3, – 4), (1, – 6) (2, – 1), (2, 5) SOLUTION m = – 6 – (– y 2 – y 1 y 2 – y 4) 1 = x 2 – x 1 – 3 2 – x 1 = – 2 = 1 Because m > 0, the line rises. m = 5 – (– 1) y 2 – y 1 = x 2 – x 1 x 2 – 2 2 – x 1 = 6 0 Because m is undefined, the line is vertical.

Comparing Steepness of Lines The slope of a line tells you more than whether the line rises, falls, is horizontal, or is vertical. It also tells you the steepness of the line. For two lines with positive slopes, the line with the greater slope is steeper. For two lines with negative slopes, the line with the slope of greater absolute value is steeper.

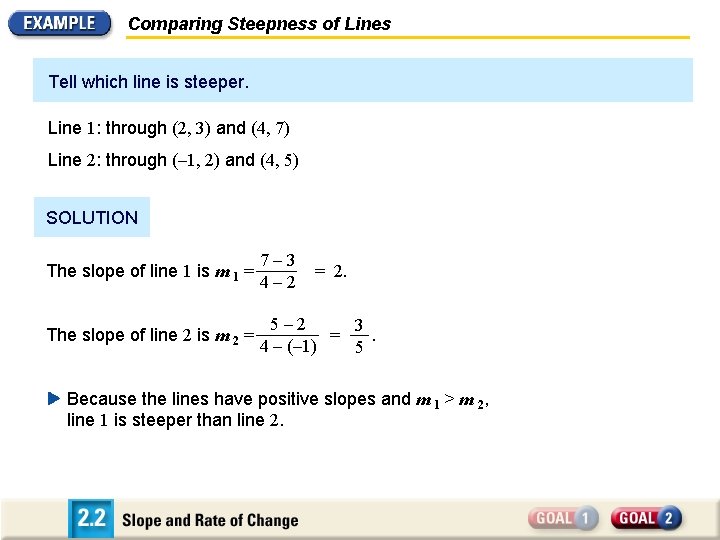
Comparing Steepness of Lines Tell which line is steeper. Line 1: through (2, 3) and (4, 7) Line 2: through (– 1, 2) and (4, 5) SOLUTION The slope of line 1 is m 1 = 7 – 3 4 – 2 The slope of line 2 is m 2 = 5 – 2 3 = . 4 – (– 1) 5 = 2. Because the lines have positive slopes and m 1 > m 2, line 1 is steeper than line 2.

Classifying Parallel and Perpendicular Lines Slope can be used to determine whether two different (nonvertical) lines are parallel or perpendicular. Two lines in a plane are parallel if they do not intersect. Two lines in a plane are perpendicular if they intersect to form a right angle. SLOPES OF PARALLEL AND PERPENDICULAR LINES Consider two different nonvertical lines 1 and 2 with Parallel Lines The lines are parallel if and only if they Perpendicular The lines are perpendicular if have the ifsame and only their slopes are negative reciprocals of each other. 1 or 2 m 1 m 2 = – 1 m 1 = – m 1 = m m 2 slopes m 1 and m 2. y x

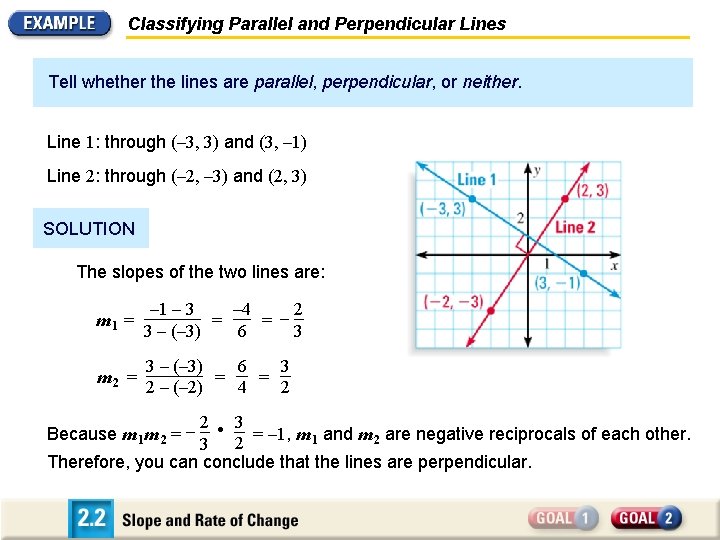
Classifying Parallel and Perpendicular Lines Tell whether the lines are parallel, perpendicular, or neither. Line 1: through (– 3, 3) and (3, – 1) Line 2: through (– 2, – 3) and (2, 3) SOLUTION The slopes of the two lines are: m 1 = – 1 – 3 – 4 2 = = – 3 – (– 3) 6 3 m 2 = 3 3 – (– 3) 6 = = 2 2 – (– 2) 4 3 – 2 • Because m 1 m 2 = = – 1, m 1 and m 2 are negative reciprocals of each other. 3 2 Therefore, you can conclude that the lines are perpendicular.

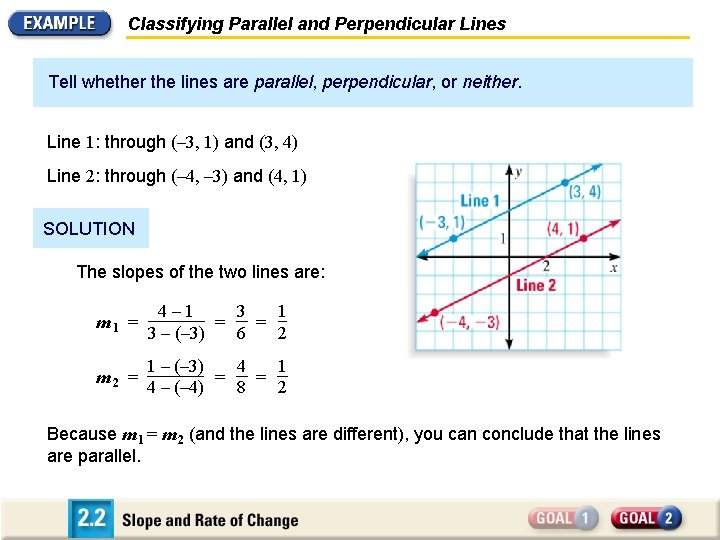
Classifying Parallel and Perpendicular Lines Tell whether the lines are parallel, perpendicular, or neither. Line 1: through (– 3, 1) and (3, 4) Line 2: through (– 4, – 3) and (4, 1) SOLUTION The slopes of the two lines are: m 1 = 4 – 1 3 1 = = 3 – (– 3) 6 2 m 2 = 1 1 – (– 3) 4 = = 2 4 – (– 4) 8 Because m 1 = m 2 (and the lines are different), you can conclude that the lines are parallel.

Using Slope in Real Life In a home repair manual the following ladder safety guideline is given. Adjust the ladder until the distance from the base of the ladder to the wall is at least one quarter of the height where the top of the ladder hits the wall. For example, a ladder that hits the wall at a height of 12 feet should have its base at least 3 feet from the wall. Find the maximum recommended slope for a ladder. SOLUTION A ladder that hits the wall at a height of 12 feet with its base about 3 feet from rise 12 the wall has slope m = = = 4. 3 run The maximum recommended slope is 4.

Using Slope in Real Life In a home repair manual the following ladder safety guideline is given. Adjust the ladder until the distance from the base of the ladder to the wall is at least one quarter of the height where the top of the ladder hits the wall. Find the minimum distance a ladder’s base should be from a wall if you need the ladder to reach a height of 20 feet. SOLUTION 4 Letrise x represent the minimum distance that the ladder’s Write a proportion. = 1 runshould base be from the wall for the ladder to safely reach of 20 feet. 4 20 a height The rise is 20 and the run is x. = x 1 20 = 4 x 5 = x Cross multiply. Solve for x. The ladder’s base should be at least 5 feet from the wall.

Finding the Slope of a Line In real-life problems slope is often used to describe an average rate of change. These rates involve units of measure, such as miles per hour or dollars per year. DESERTS In the Mojave Desert in California, temperatures can drop quickly from day to night. Suppose the temperature drops from 100ºF at 2 P. M. to 68ºF at 5 A. M. Find the average rate of change and use it to determine the temperature at 10 P. M. SOLUTION Average rate of change = = Change in temperature Change in time – 32ºF 68ºF – 100ºF – 2ºF per hour = 5 A. M. – 2 P. M. 15 hours Because 10 P. M. is 8 hours after 2 P. M. , the temperature changed 8(– 2ºF) = – 16ºF. That means the temperature at 10 P. M. was about 100ºF – 16ºF = 84ºF.