Sistemi di numerazione La rappresentazione pi semplice poco

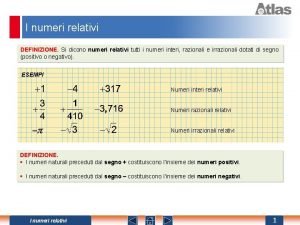
Sistemi di numerazione • La rappresentazione più semplice: | | …. poco rappresentativa; difficoltà di memorizzazione • Numeri romani: I, III, IV, V, VII, VIII, IX, X, … 1997 MCMXCVII problemi di utilizzo nelle operazioni e nella rappresentazione di numeri “grandi” Università di Pavia - corso di Fondamenti di Informatica 52

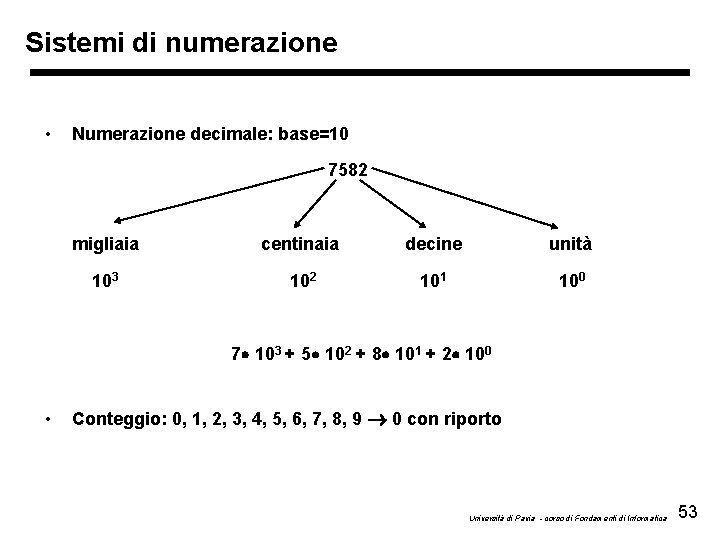
Sistemi di numerazione • Numerazione decimale: base=10 7582 migliaia centinaia decine unità 103 102 101 100 7 103 + 5 102 + 8 101 + 2 100 • Conteggio: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0 con riporto Università di Pavia - corso di Fondamenti di Informatica 53

Rappresentazione di numeri interi • Si sceglie una base b. • Si scelgono b simboli che rappresentano i numeri da 0 a b-1 (cifre). • I numeri sono rappresentati dai coefficienti del polinomio per le potenze della base • Indichiamo la base del sistema di numerazione con il pedice Nb = As As-1 … A 1 A 0 0 Ai b - 1 Valore Nb = As bs + As-1 bs-1 + … + A 1 b 1 + A 0 b 0 • La rappresentazione è posizionale poiché il peso associato alla generica cifra Ai dipende dalla posizione di Ai Università di Pavia - corso di Fondamenti di Informatica 54

Sistemi di numerazione Numerazione binaria: base=2 • Conteggio: Binario Decimale 0 0 1 1 10 2 11 3 10, 11 0 riporto 100 4 100, … 101 5 110 6 111 7 1000 8 1001 9 0, 1 0 riporto Corrispondenza binario-decimale Università di Pavia - corso di Fondamenti di Informatica 55

Sistemi di numerazione Numerazione binaria: base 2. Simboli usati: 0, 1 1 0 1 28=256 29=512 0 1 26=64 27=128 1 1 24=16 25=32 0 1 22=4 23=8 0 2 20=1 21=2 1 29 + 0 28 + 1 27 + 0 26 + 1 25 + 1 24 + 1 23 + 0 22 + 1 21 + 0 20 = = 512+128+32+16+8+2=698 10 Università di Pavia - corso di Fondamenti di Informatica 56

Sistemi di numerazione Numerazione ottale: base 8 Simboli usati: 0, 1, 2, 3, 4, 5, 6, 7 Esempio: 37158 3 83 + 7 82 + 1 81 + 5 80 = = 3 512 + 7 64 + 8 + 5 = = 1536+448+8+5 = 1997 10 Università di Pavia - corso di Fondamenti di Informatica 57

Sistemi di numerazione Numerazione esadecimale : base 16 Simboli usati: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Esempio: 7 C D 16 7 162 + 12 161 + 13 160 = = 7 256 + 12 16 + 13 = = 1792+13 = 1997 10 Università di Pavia - corso di Fondamenti di Informatica 58

Sistemi di numerazione: esempi • Base 2 1 0 2 = 23 + 2 = 10 10 1 1 0 0 2 = 26 + 25 + 22 = 100 10 1 1 1 0 0 0 2 = 29 + 28 + 27 + 26 + 25 + 23 = 1000 10 • Base 8 1 2 8 = 8 + 2 = 10 1 4 4 8 = 82 + 4 8 + 4 = 100 1 7 5 0 8 = 83 + 7 82 + 5 8 = 512 + 448 + 40 = 1000 10 Università di Pavia - corso di Fondamenti di Informatica 59

Sistemi di numerazione: esempi • Base 16 A 16 = 10 10 6 4 16 = 6 16 + 4 = 100 10 3 E 8 16 = 3 162 + 14 16 + 8 = 768 + 224 + 8 = 1000 10 F 16 = 15 10 5 E 16 = 5 16 + 14 = 94 10 7 1 B 16 = 7 162 + 1 16 + 11 = 1792 + 16 + 11 = 1819 10 Università di Pavia - corso di Fondamenti di Informatica 60

Sistemi di numerazione: esempi b = 10, N = 14320 10 N = 1 104 + 4 103 + 3 102 + 2 10 + 0 1 b = 2, N = 110100 2 N = 1 25 + 1 24 + 0 23 + 1 22 + 0 1 = 32 + 16 + 4 = 52 10 b = 8, N = 3216 8 N = 3 83 + 2 82 + 1 8 + 6 = 1536 + 128 + 6 = 1678 10 b = 16, N = AB 9 E 16 N = 10 163 + 11 162 + 9 16 + 15 = 40960 + 2816 + 144 + 15 = 43935 10 Università di Pavia - corso di Fondamenti di Informatica 61

Conversione di base Per la parte intera: • Dato un numero in una base A, si vuole rappresentarlo in base B, cioè: N A = N B = x 0 + B (x 1 + B (…B xs)…) • Se dividiamo N A per la nuova base B, otteniamo un quoziente N 1 ed un resto R. Uguagliando: N A = R + B N 1 = x 0 + B (x 1 + B (x 2 + … ) ) da cui: x 0 = R (x 1 + B (x 2 + … ) ) = N 1 • Iterando il procedimento con N 1 al posto di N A, si ottengono tutti i coefficienti del polinomio nelle potenze di B, cioè la codifica di N A nella nuova base, e quindi N B Università di Pavia - corso di Fondamenti di Informatica 62

Conversione di base 1258 629 314 157 78 39 19 9 4 2 1 0 0 1 0 1 1 1 0 0 1 1258 10 = 10011101010 2 1258 157 19 2 0 2 5 3 2 1258 10 = 2352 8 1258 78 4 0 10 14 4 1258 10 = 4 EA 16 Università di Pavia - corso di Fondamenti di Informatica 63

Conversione di base: numeri frazionari Nb = 0 , A-1 A-2 A-3 A-4 A-5 Valore Nb = A-1 b-1 + A-2 b-2 + A-3 b-3 + A-4 b-4 + A-5 b-5 In generale: Qb = As As-1 … A 1 A 0 , A-1 A-2 A-3 … A-R 0 Ai b - 1 Valore Qb = As bs + As-1 bs-1 + … + A 1 b 1 + A 0 b 0 + + A-1 b-1 + A-2 b-2 + A-3 b-3 + … + A-R b-R Esempi: b = 10, N = 325, 23 10 N = 3 102 + 2 101 + 5 + 2 10 -1 + 3 10 -2 b = 2, N = 101, 01 2 N = 1 22 + 1 2 -2 = 4 + 1 + 0, 25 = 5, 25 10 Università di Pavia - corso di Fondamenti di Informatica 64

Conversione di base Per la parte frazionaria: • Dato un numero in una base A, si vuole rappresentarlo in base B, cioè: FA = FB = B-1(x-1 + B-1(x-2 + B-1(…B-1 x-r)…)) • Se moltiplichiamo F A per la nuova base B, otteniamo una parte intera I ed una parte frazionaria F 1. Uguagliando: FA B = I + F 1 da cui: x-1 = I B-1(x-2 + B-1(…B-1 x-r)…) = F 1 • Iterando il procedimento con F 1 al posto di FA, si ottengono i coefficienti del polinomio nelle potenze di B, cioè la codifica di FA nella nuova base, e quindi FB. Il procedimento termina quando Fl = 0, oppure quando si è raggiunta la precisione desiderata (errore < B-r se ci si ferma al termine x-r) Università di Pavia - corso di Fondamenti di Informatica 65

Conversione di base: numeri frazionari 0. 59375 1. 18750 0. 37500 0. 75000 1. 50000 1. 00000 1 0 0 1 1 0. 59375 10= 0. 10011 2 0. 59375 4. 75000 6. 00000 4 6 0. 59375 10= 0. 46 8 0. 59375 9. 50000 8. 00000 9 8 0. 59375 10= 0. 98 16 Università di Pavia - corso di Fondamenti di Informatica 66

CONVERTIRE IL NUMERO 58, 0710 IN BINARIO PARTE INTERA PARTE FRAZIONARIA 58 = 29 x 2+0 X 0=0 29 = 14 x 2+1 X 1=1 14 = 7 x 2+0 X 2=0 7 = 3 x 2+1 X 3=1 3 = 1 x 2+1 X 4=1 1 = 0 x 2+1 X 5=1 0, 07 x 2=0. 14 X-1=0 0, 14 x 2=0. 28 X-2=0 0, 28 x 2=0. 56 X-3=0 0, 56 x 2=1. 12 X-4=1 0, 12 x 2=0. 24 X-5=0 0, 24 x 2=0. 48 X-6=0 0, 48 x 2=0. 96 X-7=0 0, 96 x 2=1. 92 X-8=1 0, 92 x 2=1. 84 X-9=1 (TRONCHIAMO QUI) IL NUMERO IN BINARIO È: 111010, 00011 Università di Pavia - corso di Fondamenti di Informatica 67

CONVERTIRE IL NUMERO 4287, 31210 IN ESADECIMALE PARTE INTERA: 4287: 16=267 : 16= 16 16 : 16= 1 1 : 16= 0 PARTE FRAZIONARIA RESTO=15 F RESTO=11 B RESTO= 0 0 RESTO= 1 1 0, 312 x 16=4, 992 4 0, 992 x 16=15, 872 F 0, 872 x 16=13, 952 D 0, 952 x 16=15, 232 F 4287, 31210 ~ 10 BF, 4 FDF… 16 1 X 163 = 4096 11 X 161 = 176 15 X 160 = 15 4 X 16 -1 = 0, 250 15 X 16 -2 = 0, 04859. . . _________________ = 4287, . . Università di Pavia - corso di Fondamenti di Informatica 68

Conversione di un numero dalla base β 1 alla base β 2 quando β 2= β 1 k dove K è un intero ≥ 2 ESEMPIO: β 1=2, β 2=8=23 N 2 = dk dk-1. . . d 5 d 4 d 3 d 2 d 1 d 0 = dk 2 k+…. +d 525+d 424+d 323+d 222+d 121+d 020 = …. +(d 522+d 421+d 320)23+(d 222+d 121+d 020)20 = ch 23*h+…. +c 223*2+c 123*1+c 023*0 con 0 ci 7 = ch 8 h+…. +c 282+c 181+c 080 N 8= ch ch-1. . . c 5 c 4 c 3 c 2 c 1 c 0 Quindi se una base è potenza dell’altra, con esponente K, la conversione è molto semplice: basta sostituire ogni gruppo di K cifre del numero in una base (β 1) con la cifra corrispondente nell’altra base (β 2) o viceversa. N. B. se il numero di bit non è multiplo di K aggiungere gli 0 necessari a renderlo tale in posizioni che non modifichino il significato del numero. Università di Pavia - corso di Fondamenti di Informatica 69

Conversioni fra basi diverse Esempio: 16 2 0 0000 8 1000 1 0001 9 1001 2 0010 A 1010 3 0011 B 1011 4 0100 C 1100 5 0101 D 1101 6 0110 E 1110 7 0111 F 1111 Università di Pavia - corso di Fondamenti di Informatica 70

Conversioni fra basi diverse: esempi • • 100111010102 125810 10|011|101|0102 23528 100|1110|10102 4 EA 16 0. 10011000002 0. 5937510 0. 100|110|000|02 0. 468 0. 1001|1000|002 0. 9816 Si può fare anche il passaggio inverso: • 1 F 516 1|1111|01012 • 75268 111|101|010|1102 • 752616 111|0101|0010|01102 Università di Pavia - corso di Fondamenti di Informatica 71

Conversione di base: numeri frazionari 0. 1 0. 2 0. 4 0. 8 1. 6 1. 2 0. 4 0. 8 …. 0 0 0 1 1 0 0 Può accadere che a un numero decimale non periodico corrisponda un numero binario, ottale o esadecimale periodico 0. 1 0. 8 6. 4 3. 2 1. 6 4. 8 …. 0 6 3 1 4 0. 1 1. 6 9. 6 …. 1 9 Università di Pavia - corso di Fondamenti di Informatica 72

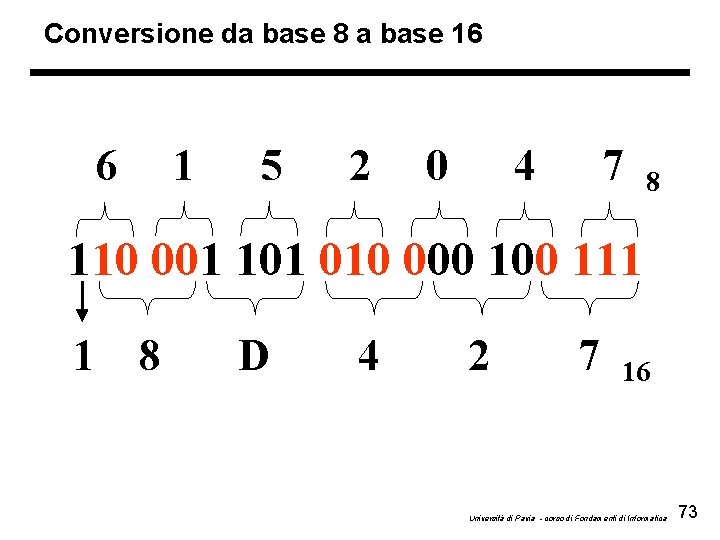
Conversione da base 8 a base 16 6 1 5 2 0 4 7 8 110 001 101 010 000 111 1 8 D 4 2 7 16 Università di Pavia - corso di Fondamenti di Informatica 73

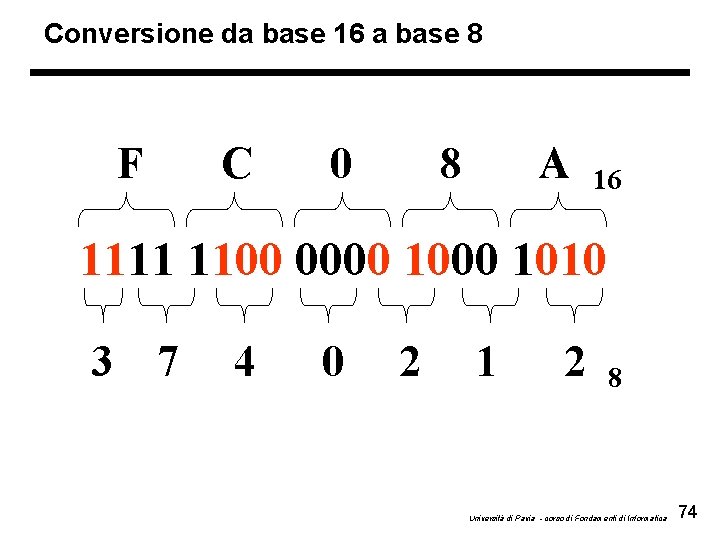
Conversione da base 16 a base 8 F C 0 8 A 16 1111 1100 0000 1010 3 7 4 0 2 1 2 8 Università di Pavia - corso di Fondamenti di Informatica 74

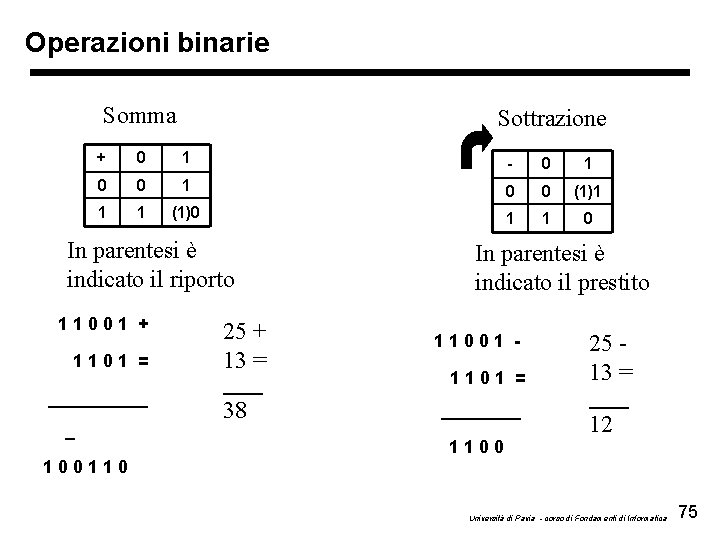
Operazioni binarie Somma Sottrazione + 0 1 - 0 1 0 0 (1)1 1 1 (1)0 1 1 0 In parentesi è indicato il riporto 11001 + 1101 = _____ _ 25 + 13 = ____ 38 In parentesi è indicato il prestito 11001 1101 = ____ 1100 25 13 = ____ 12 100110 Università di Pavia - corso di Fondamenti di Informatica 75

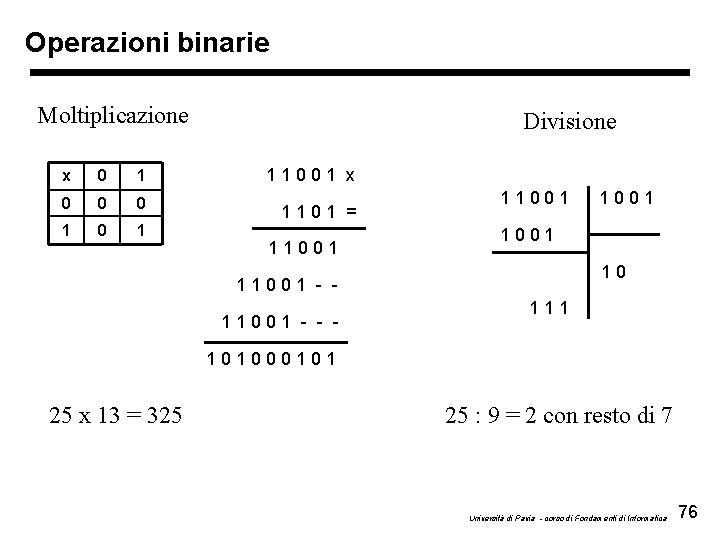
Operazioni binarie Moltiplicazione Divisione x 0 1 11001 x 0 0 0 1 1101 = 11001 10 11001 - - - 1001 111 101000101 25 x 13 = 325 25 : 9 = 2 con resto di 7 Università di Pavia - corso di Fondamenti di Informatica 76

Rappresentazione dei numeri nei calcolatori • L’unità minima di informazione nei calcolatori è il bit. Il bit corrisponde ad un sistema fisico dotato di stati stabili: passa/non passa corrente, tensione alta/bassa, condensatore scarico/carico, ecc. • I calcolatori si basano sul sistema numerico binario (cifre 0 e 1) • Si utilizza cioè un insieme di bit per rappresentare le cifre binarie. Il numero di bit utilizzati è generalmente un multiplo di 8 (cioè si utilizzano 1, 2, 4, 8 byte) Università di Pavia - corso di Fondamenti di Informatica 77

Rappresentazione dei numeri nei calcolatori • Si consideri un byte (8 bit). Un byte permette di rappresentare 28 stati differenti; può pertanto memorizzare 256 diverse configurazioni corrispondenti ai primi 256 numeri naturali (0 -255) b 7 b 6 b 5 b 4 b 3 b 2 b 1 b 0 Nella rappresentazione in valore assoluto: N= b 7 27 + b 6 26 + b 5 25 + b 4 24 + b 3 23 + b 2 22 + b 1 21 + b 0 20 0 0 1 0 1 N=37 Università di Pavia - corso di Fondamenti di Informatica 78

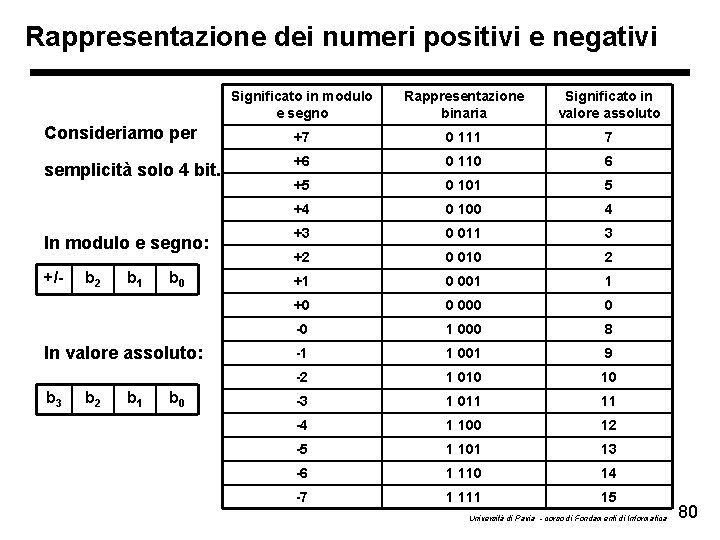
Rappresentazione dei numeri positivi e negativi • Esiste un problema: come rappresentare i numeri negativi • Prima soluzione: rappresentazione in Modulo e Segno (anche detta Binario Naturale) Si utilizza un bit per rappresentare il segno del numero considerato 0 + (numero positivo) 1 - (numero negativo) Se consideriamo un byte, rimangono ora 7 bit per il modulo del numero: i numeri rappresentabili sono perciò [0 -127] +/- b 6 b 5 b 4 b 3 b 2 b 1 b 0 Università di Pavia - corso di Fondamenti di Informatica 79

Rappresentazione dei numeri positivi e negativi Significato in modulo e segno Rappresentazione binaria Significato in valore assoluto Consideriamo per +7 0 111 7 semplicità solo 4 bit. +6 0 110 6 +5 0 101 5 +4 0 100 4 +3 0 011 3 +2 0 010 2 +1 0 001 1 +0 0 000 0 -0 1 000 8 -1 1 001 9 -2 1 010 10 -3 1 011 11 -4 1 100 12 -5 1 101 13 -6 1 110 14 -7 1 111 15 In modulo e segno: +/- b 2 b 1 b 0 In valore assoluto: b 3 b 2 b 1 b 0 Università di Pavia - corso di Fondamenti di Informatica 80

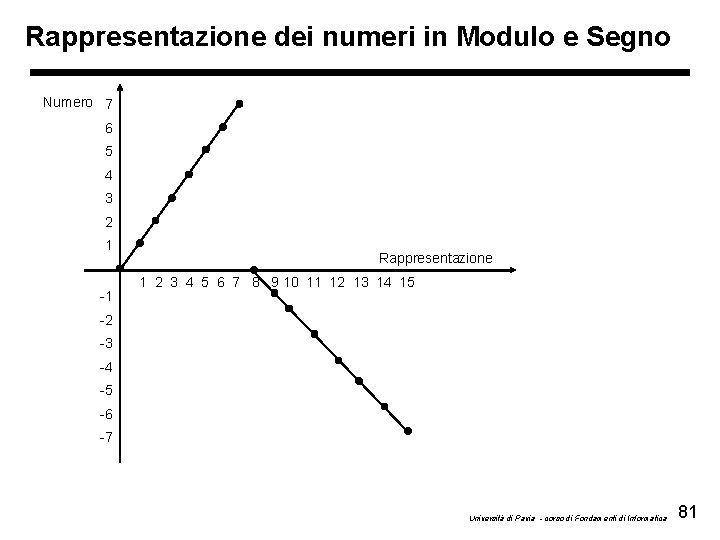
Rappresentazione dei numeri in Modulo e Segno Numero 7 6 5 4 3 2 1 -1 Rappresentazione 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -2 -3 -4 -5 -6 -7 Università di Pavia - corso di Fondamenti di Informatica 81

Rappresentazione dei numeri in Modulo e Segno • Esistono due rappresentazioni diverse dello 0 distanti 2 n-1 fra di loro, se n sono i bit usati per la rappresentazione (8 con 4 bit) • Un incremento binario nella rappresentazione corrisponde ad un incremento per numeri positivi, ma un decremento per numeri negativi • Numero minimo: -2 n-1+1 • Numero massimo: 2 n-1 -1 Università di Pavia - corso di Fondamenti di Informatica 82

Rappresentazione in modulo e segno: problemi • Addizione e sottrazione sono le operazioni di cui si deve disporre per poter realizzare qualsiasi operazione aritmetica più complessa • Si supponga che il calcolatore abbia una “Unità Aritmetica” che realizzi indipendentemente le due operazioni. • Di fronte ad una somma algebrica, il calcolatore dovrebbe: – confrontare i due segni – se uguali, attivare il circuito di addizione – se diversi, identificare il maggiore (in valore assoluto) ed attivare il circuito di sottrazione – completare il risultato con il segno corretto • I passi indicati non sono eseguibili contemporaneamente perché ognuno dipende dai precedenti • In pratica per effettuare somma e sottrazione si ricorre ad un unico circuito, utilizzando un metodo che permette di evitare le operazioni di confronto Università di Pavia - corso di Fondamenti di Informatica 83

Complemento alla base di un numero • Nella rappresentazione in complemento alla base con n cifre le bn combinazioni rappresentano numeri positivi e negativi. • In particolare: le combinazioni da 0 a bn: 2 - 1 rappresentano i numeri positivi, rispettando la usuale rappresentazione posizionale; Le combinazioni da bn: 2 fino a bn – 1 rappresentano i numeri negativi, con la seguente definizione: dato un numero positivo X, il suo corrispondente negativo è dato da: bn-X Università di Pavia - corso di Fondamenti di Informatica 84

Complemento alla base – 1 di un numero • Nella rappresentazione in complemento alla base – 1 con n cifre le bn combinazioni rappresentano numeri positivi e negativi. • In particolare: le combinazioni da 0 a bn: 2 - 1 rappresentano i numeri positivi, rispettando la usuale rappresentazione posizionale; Le combinazioni da bn: 2 fino a bn – 1 rappresentano i numeri negativi, con la seguente definizione: dato un numero positivo X, il suo corrispondente negativo è dato da: (bn-1)-X Università di Pavia - corso di Fondamenti di Informatica 85

Complemento alla base Esempio b=10, n=2; 102 configurazioni: i numeri da 0 a 49 rappresentano i positivi, con il consueto significato; da 50 a 99 i negativi come previsto dal complemento (-1 -> 99, -2 -> 98, … , -49 -> 51, -50 -> 50). X=36; -X in complemento alla base (si dice complemento a 10) è: 102 - X = 100 - 36 = 64 b=10, n=4; i numeri da 0 a 4999 rappresentano i positivi; da 5000 a 9999 i negativi (-1 -> 9999, -2 -> 9998, … , -4999 -> 5001, -5000 -> 5000) X=1630; -X in complemento alla base è: 10000 - 1630 = 8370 Regola pratica per trovare l’equivalente negativo di un numero positivo, in complemento a 10: il significativa fa significativa cifra prima della quali; si eriportano tali si Università di Pavia - corso di Fondamenti di Informatica complemento a 10, di tutte le altre il complemento a 9 86

Complemento alla base b=2, n=5 b=2, n=7 Positivi da 0 a 0111111 Negativi da 1000000 a 1111111 a 11111 X=0011000; trovo -X X = 01011; trovo -X 10000000 - 100000 - 0011000= 01011= 10101 1101000 Regola pratica per trovare l’equivalente negativo di un numero positivo, in complemento a 2 : partendo dal bit meno significativo, si riportano invariati tutti i bit fino al primo bit a 1 compreso; si complementano i rimanenti bit (0 1, 1 0) Università di Pavia - corso di Fondamenti di Informatica 87

Complemento alla base -1 X=36, b=10, n=2 in complemento alla base -1 è: 99 - 36 = 63 Si ottiene complementando a 9 ogni singola cifra X=01011, b=2, n=5 -X in complemento alla base -1 è: (25 - 1) - X = (100000 - 1) - X = 11111 - 01011 = 10100 Si ottiene complementando ogni singolo bit (0 1, 1 0) Università di Pavia - corso di Fondamenti di Informatica 88

Complemento alla base • La rappresentazione dei numeri negativi in complemento alla base si può ottenere anche sommando 1 alla rappresentazione dei numeri negativi in complemento alla base -1 (per definizione) Cb = b n - X Cb-1 = (bn - 1) - X Cb - Cb-1 = 1 C 10 (36) = 64 che rappresenta - 36 C 9 (36) = 63 che rappresenta - 36 Università di Pavia - corso di Fondamenti di Informatica 89

Complementi alla base e alla base -1 Nelle rappresentazioni in complemento alla base e in complemento alla base -1 le rappresentazioni dei numeri negativi sono definite solo quando si è stabilito il numero di cifre. In complemento alla base [e in complemento alla base -1] per X=36, b=10, n=2: -X = 64 [63] In complemento alla base [e in complemento alla base -1] per X=36, b=10, n=3: -X = 964 [963] N. B: Tutti i numeri ottenuti rappresentano – 36 !!! Università di Pavia - corso di Fondamenti di Informatica 90

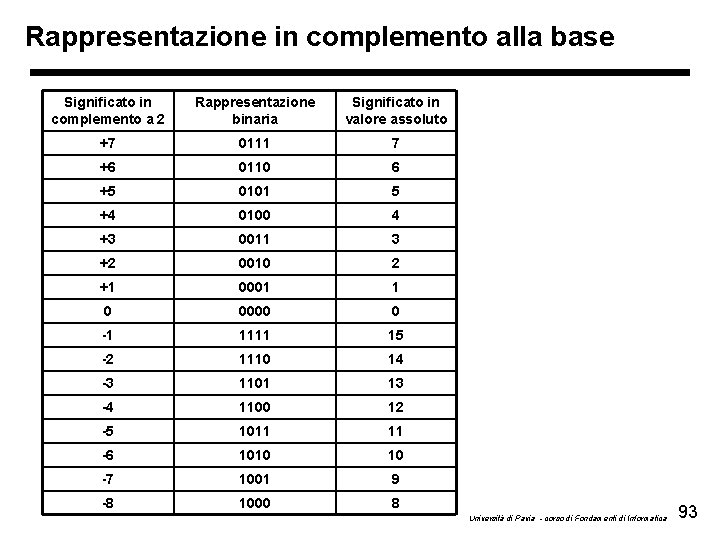
Rappresentazione in complemento: Riepilogo • Rappresentazione in complemento a 2: i numeri positivi sono rappresentati dal loro modulo e hanno il bit più significativo (segno) posto a 0. I numeri negativi sono rappresentati dalla quantità che manca al numero positivo per arrivare alla base elevata al numero di cifre utilizzate, segno compreso. Pertanto i numeri negativi hanno il bit del segno sempre a 1 • Metà delle configurazioni sono perciò riservate ai numeri positivi e metà ai numeri negativi • Discorsi analoghi possono essere fatti per basi diverse da 2: in base 10 un numero è negativo se la prima cifra è 5, in base 8 se 4, in base 16 se 8 Università di Pavia - corso di Fondamenti di Informatica 91

Rappresentazione in complemento alla base Con n bit a disposizione: • Il numero minimo rappresentabile è -2 n-1 • Il numero massimo rappresentabile è 2 n-1 - 1 • -1 è rappresentato da tutti 1 qualunque sia il numero di bit considerato • Il numero può essere interpretato considerando il bit più significativo con segno negativo b 3 b 2 b 1 b 0 N= - b 3 23 + b 2 22 + b 1 21 + b 0 20 Università di Pavia - corso di Fondamenti di Informatica 92

Rappresentazione in complemento alla base Significato in complemento a 2 Rappresentazione binaria Significato in valore assoluto +7 0111 7 +6 0110 6 +5 0101 5 +4 0100 4 +3 0011 3 +2 0010 2 +1 0001 1 0 0000 0 -1 1111 15 -2 1110 14 -3 1101 13 -4 1100 12 -5 1011 11 -6 1010 10 -7 1001 9 -8 1000 8 Università di Pavia - corso di Fondamenti di Informatica 93

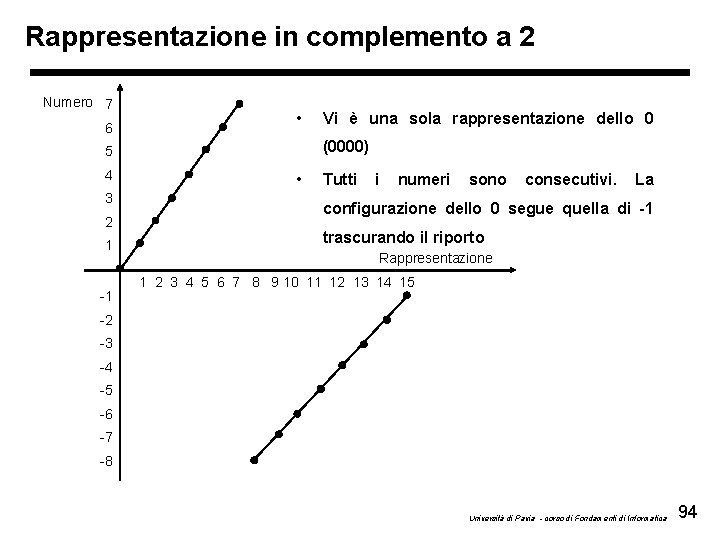
Rappresentazione in complemento a 2 Numero 7 6 • (0000) 5 4 3 2 1 -1 Vi è una sola rappresentazione dello 0 • Tutti i numeri sono consecutivi. La configurazione dello 0 segue quella di -1 trascurando il riporto Rappresentazione 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -2 -3 -4 -5 -6 -7 -8 Università di Pavia - corso di Fondamenti di Informatica 94

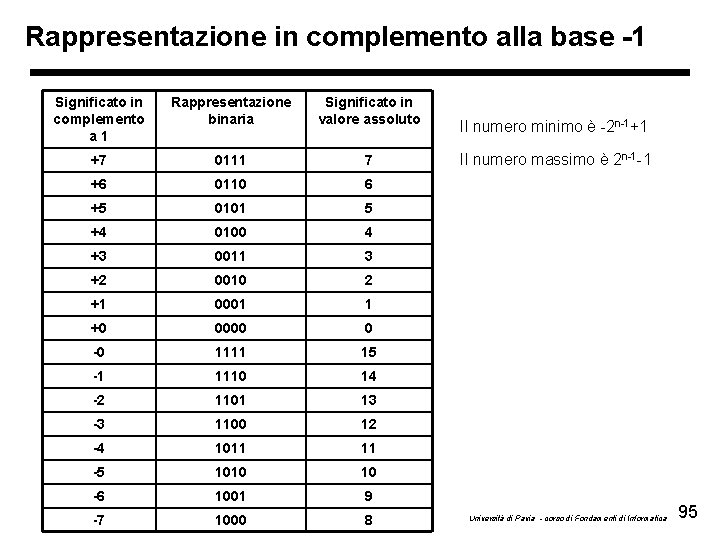
Rappresentazione in complemento alla base -1 Significato in complemento a 1 Rappresentazione binaria Significato in valore assoluto +7 0111 7 +6 0110 6 +5 0101 5 +4 0100 4 +3 0011 3 +2 0010 2 +1 0001 1 +0 0000 0 -0 1111 15 -1 1110 14 -2 1101 13 -3 1100 12 -4 1011 11 -5 1010 10 -6 1001 9 -7 1000 8 Il numero minimo è -2 n-1+1 Il numero massimo è 2 n-1 -1 Università di Pavia - corso di Fondamenti di Informatica 95

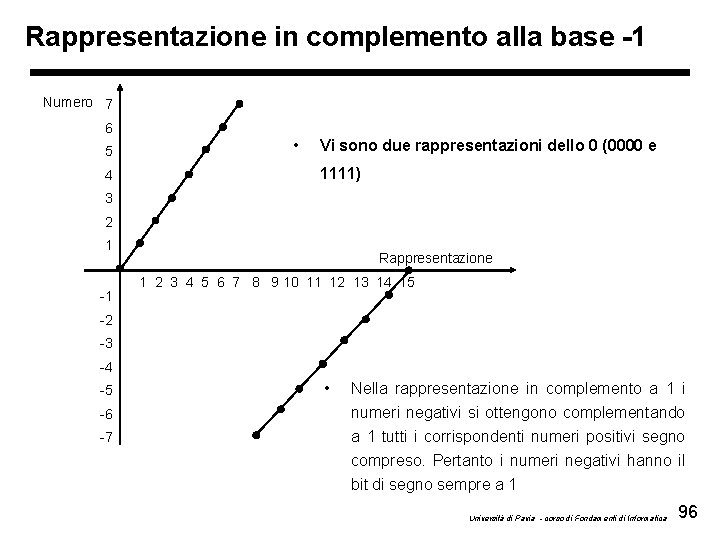
Rappresentazione in complemento alla base -1 Numero 7 6 5 4 • Vi sono due rappresentazioni dello 0 (0000 e 1111) 3 2 1 -1 Rappresentazione 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -2 -3 -4 -5 -6 -7 • Nella rappresentazione in complemento a 1 i numeri negativi si ottengono complementando a 1 tutti i corrispondenti numeri positivi segno compreso. Pertanto i numeri negativi hanno il bit di segno sempre a 1 Università di Pavia - corso di Fondamenti di Informatica 96

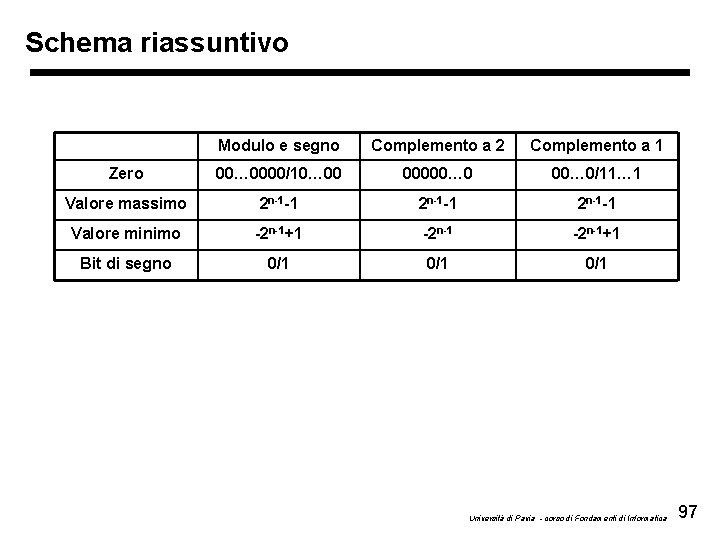
Schema riassuntivo Modulo e segno Complemento a 2 Complemento a 1 Zero 00… 0000/10… 00 00000… 0/11… 1 Valore massimo 2 n-1 -1 Valore minimo -2 n-1+1 Bit di segno 0/1 0/1 Università di Pavia - corso di Fondamenti di Informatica 97

Rappresentazione di interi in complemento a 2 • Con 1 byte (8 bit) max = 27 -1 = 127 min = -27 = -128 • Con 2 byte (16 bit) max = 215 -1 = 32767 min = -215 = -32768 • Con 4 byte (32 bit) max = 231 -1 = 2 147 483 647 min = -231 = -2 147 483 648 Università di Pavia - corso di Fondamenti di Informatica 98

Utilità del complemento alla base • Con la tecnica del complemento si può utilizzare un solo circuito per effettuare sia l’addizione, sia la sottrazione • Operiamo in base 10 e vogliamo calcolare A – B. • Si supponga di conoscere il risultato dell’operazione 10 - B (complemento a 10 di B). Allora: A - B = A + (10 - B) a condizione che si trascuri il riporto • Analogo discorso con k cifre purché si disponga del risultato dell’operazione 10 k – B (complemento a 10 k). Si ricordi sempre di fissare il numero di cifre • Se operiamo in base 2, con k cifre: A - B = A + (2 k - B) a condizione che si trascuri il riporto • Se si utilizza la tecnica del complemento alla base -1 occorre sommare il riporto al risultato finale Università di Pavia - corso di Fondamenti di Informatica 99

Operazioni aritmetiche in complemento: esempi A B 43517 26106 = 73894) ______ A-B 17411 A B 01001 00110 = 11010) ______ A-B 00011 A B A-B 42 A 61 00 B 02 = ______ 41 F 5 F Usando il complemento 43517 + 73894 = (in complemento -26106 = _______ 117411 01001 + 11010 = ______ 100011 42 A 61 + FF 4 FE = ______ 141 F 5 F (riporto da non considerare) (in complemento -00110 = (riporto da non considerare) (in complem. -00 B 02 = FF 4 FE) (riporto da non considerare) Università di Pavia - corso di Fondamenti di Informatica 100

Operazioni aritmetiche in complemento: esempi Con il complemento alla base -1 occorre sommare il riporto al risultato finale A 43517 - 43517 + 17410 + B 26106 = ______ 73893 = _______ 1= _______ A-B 17411 117410 A 01001 - 01001 + 00010 + B 00110 = ______ 11001 = _______ 1= _______ A-B 00011 A 42 A 61 - 42 A 61 + 41 F 5 E + B 00 B 02 = ______ FF 4 FD = _______ 1= _______ A-B 41 F 5 F 100010 17411 141 F 5 E 00011 41 F 5 F Università di Pavia - corso di Fondamenti di Informatica 101

Operazioni aritmetiche in complemento Esempi con 6 cifre binarie Complemento a 2 Complemento a 1 19 + (-17) 010011 101111 101110 1 0 (+2) 1000001 1 0 0 1 0 (+2) Università di Pavia - corso di Fondamenti di Informatica 102

Operazioni aritmetiche in complemento Esempi con 6 cifre binarie Complemento a 2 Complemento a 1 (-17) + (-2) 101111 101110 111101 1 1 0 1 (-19) 1101011 1 1 0 0 (-19) Università di Pavia - corso di Fondamenti di Informatica 103

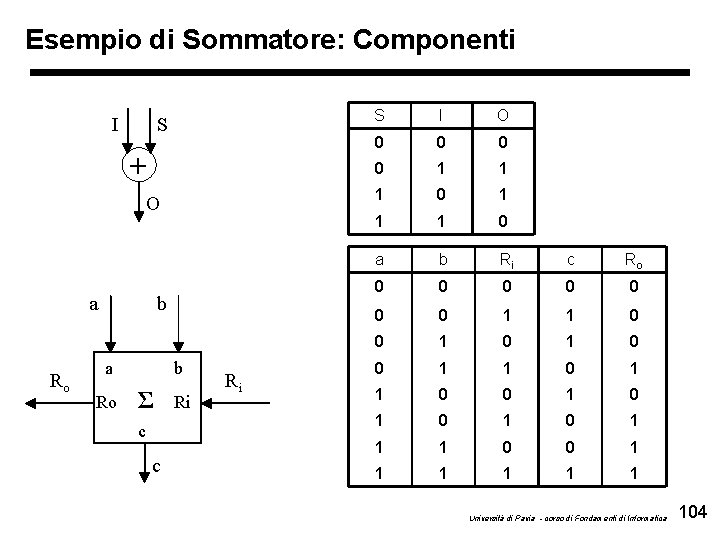
Esempio di Sommatore: Componenti I S + O a Ro b Σ c c Ri Ri S I O 0 0 1 1 1 0 a b Ri c Ro 0 0 0 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 Università di Pavia - corso di Fondamenti di Informatica 104

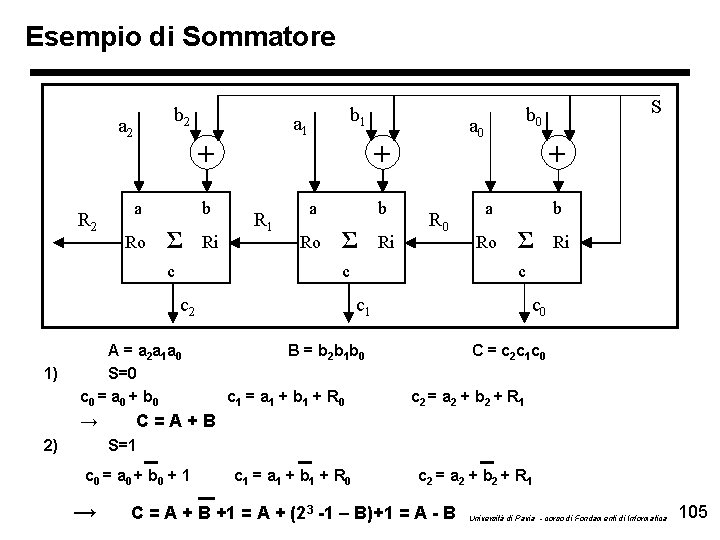
Esempio di Sommatore b 2 a 2 R 2 a 1 + a Ro b Σ Ri c b 1 R 1 a Ro b Σ A = a 2 a 1 a 0 S=0 c 0 = a 0 + b 0 → 2) Ri R 0 c c 2 1) a 0 + + a Ro b Σ Ri c c 1 c 0 B = b 2 b 1 b 0 c 1 = a 1 + b 1 + R 0 S b 0 C = c 2 c 1 c 0 c 2 = a 2 + b 2 + R 1 C=A+B S=1 c 0 = a 0 + b 0 + 1 → c 1 = a 1 + b 1 + R 0 c 2 = a 2 + b 2 + R 1 C = A + B +1 = A + (23 -1 – B)+1 = A - B Università di Pavia - corso di Fondamenti di Informatica 105

Rappresentazione di interi Esercizio: Rappresentare i numeri con 8 bit e complemento a 2 e a 1 Numero Complemento a 2 Complemento a 1 15 00001111 -15 11110001 11110000 0 00000000 1 00000001 -1 11111110 144 non rappresentabile 128 non rappresentabile -128 10000000 non rappresentabile Università di Pavia - corso di Fondamenti di Informatica 106

Operazioni aritmetiche in complemento Esempi con 6 cifre binarie 19 + 17 010011+ 010001= 1 0 0 (-28) Si sono sommati due numeri positivi e si è ottenuto un numero negativo. Il risultato corretto (+36) non è rappresentabile in complemento a 2 con 6 bit (massimo numero rappresentabile = + 31) Il fenomeno si chiama traboccamento o overflow Università di Pavia - corso di Fondamenti di Informatica 107

Operazioni aritmetiche in complemento Esempi con 6 cifre binarie Complemento a 2 Complemento a 1 (-19) + (-17) 101101+ 101100+ 101111= 101110= 1 0 1 1 1 0 0 (28) 1011010+ 1= 0 1 1 (27) Si sono sommati due numeri negativi e si è ottenuto un numero positivo. Il risultato corretto (-36) non è rappresentabile in complemento a 2 con 6 bit (minimo numero rappresentabile = -32 in C. a 2 e – 31 in C. a 1) Il fenomeno si chiama traboccamento o overflow Università di Pavia - corso di Fondamenti di Informatica 108

Somma di numeri di N bit in complemento a 2 0 A 2 N-1 -1 0 B 2 N-1 -1 -2 N-1 A < 0 0 B 2 N-1 -1 0 A 2 N-1 -1 -2 N-1 B < 0 -2 N-1 A < 0 -2 N-1 B < 0 0 S 2 N-2 -2 N-1 S < 2 N-1 -1 -2 N S < 0 Sommando due numeri positivi si ha overflow se si ottiene un numero negativo. S potrebbe non essere rappresentabile in N bit ma lo è sempre in N+1 bit. Non ci sono mai problemi di overflow. Sommando due numeri negativi si ha overflow se si ottiene un numero positivo. S potrebbe non essere rappresentabile in N bit ma lo è sempre in N+1 bit. Università di Pavia - corso di Fondamenti di Informatica 109

Esempi di somma di numeri binari 01111000+ 01101001= 11100001 11111011+ 11110000= 11101011 Complemento a 2 + 120 + + 105 = - 31 Overflow=1 - 5+ - 16 = - 21 Overflow=0 Valore Assoluto 120 + 105 = 225 Riporto=0 251 + 240 = 235 Riporto=1 Università di Pavia - corso di Fondamenti di Informatica 110

Tecnica dell’eccesso +7 1111 +6 1110 +5 1101 +4 1100 +3 1011 +2 1010 +1 1001 0 1000 -1 0111 -2 0110 -3 0101 -4 0100 -5 0011 -6 0010 -7 0001 -8 0000 • Usato per scopi particolari • Viene sommata una costante fissa, ad esempio con n bit pari a 2 n-1 (oppure 2 n-1 -1), al numero dotato di segno da rappresentare; il numero risultante viene convertito in binario. • Con questa convenzione il bit di segno è invertito Università di Pavia - corso di Fondamenti di Informatica 111