Sim Rank A Measure of StructuralContext Similarity Glen

Sim. Rank: A Measure of Structural-Context Similarity Glen Jeh & Jennifer Widom KDD 2002

Motivation Many applications require a measure of “similarity” between objects. § Web search § Shopping Recommendations § Search for “Related Works” among scientific papers But “similarity” may be domain-dependent. Can we define a generic model for similarity?

Common Ground What do all these applications have in common? data set of objects linked by a set of relations. Then, a generic concept of similarity is structural -context similarity. § “Two objects are similar if the relate to similar objects. ” Recall automorphic equivalence: § “Two objects are equivalent if the relate to equivalent objects. ”

Problem Statement Given a Graph G = (V, E), for each pair of vertices a, b ∈ V, compute a similarity (ranking) score s(a, b) based on the concept of structuralcontext similarity.

Basic Graph Model Directed Graph G = (V, E) § V = set of objects § E = set of unweighted edges § Edge (u, v) exists if there is an relation u v § I(v) = set of in-neighbors of vertex v § O(v) = set of out-neighbors of vertex v

Sim. Rank Similarity Recursive Model § “Two objects are similar if they are referenced by similar objects” § That is, a ~ b if c a and d b, and c ~ d § An object is equivalent to itself (score = 1) Example 1. Prof. A ~ Prof. B because both are referenced by Univ. 2. Student. A ~ Student. B because they are referenced by similar nodes {Prof. A, Prof. B}

Basic Sim. Rank Equation s(a, b) = similarity between a and b = average similarity between in-neighbors of a and in-neighbors of b § s(a, b) is in the range [0, 1] § If a=b, then s(a, b) = 1 § If a≠b, § C is a constant, 0 < C < 1 § if I(a) or I(b) = ∅ , then s(a, b) = 0

Decay Factor C X is identical to itself: s(x, x) = 1 a x Since we have x a and x b, should s(a, b) = 1 also? b § If the graph represented all the information about x, a, and b, then s(a, b) would ideally = 1. § But, in reality the graph does not describe everything about them, so we expect s(a, b) < 1. Therefore, the constant C expresses our limited confidence or decay with distance: s(a, b) = C ∙ average similarity of (I(a), I(b))

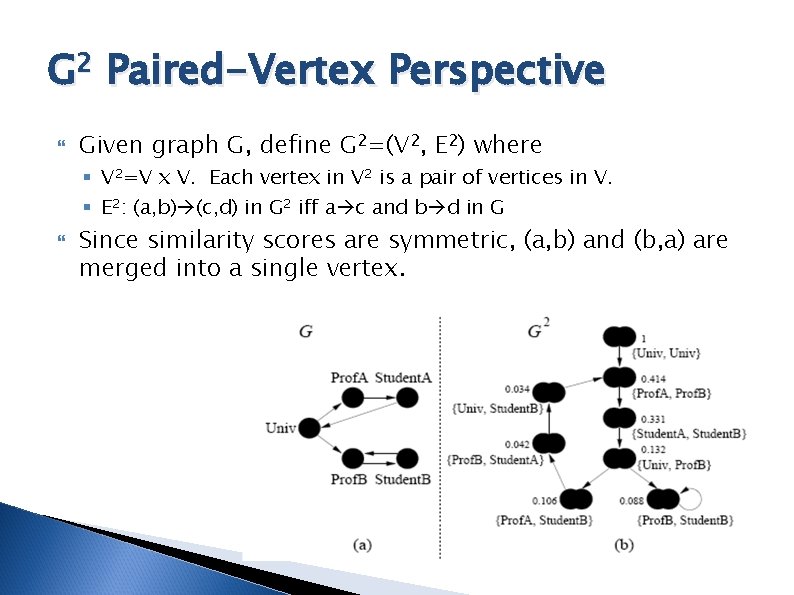
G 2 Paired-Vertex Perspective Given graph G, define G 2=(V 2, E 2) where § V 2=V x V. Each vertex in V 2 is a pair of vertices in V. § E 2: (a, b) (c, d) in G 2 iff a c and b d in G Since similarity scores are symmetric, (a, b) and (b, a) are merged into a single vertex.

Source and Flow of Similarity Sim. Rank score for a vertex (a, b) in G 2 = similarity between a and b in G. The source of similarity is self-vertices, like (Univ, Univ). Then, similarity propagates along pair-paths in G 2, away from the sources. Note that values decrease away from (Univ, Univ)

Sim. Rank in Bipartite Domains Bipartite: 2 types of objects § Example: Buyers and Items

Bipartite Sim. Rank Equations Two types of similarity: § Two buyers are similar if they buy the similar items § Out-neighbors of buyers are relevant: § Two items are similar if they are bought by similar buyers § In-neighbors of items are relevant: In general, we can use I(. ) and/or O(. ) for any graph

Mini. Max Variant Motivation: Two students A and B take the same courses: {Eng 1, Math 1, Chem 1, Hist 1} § Sim. Rank compares each course of A with each course of B § But intuitively we just want the best matching pairs: s(Eng 1 A, Eng 1 B), s(Math 1 A, Math 1 B) , etc. Solution: Two steps § Max: Pair each neighbor of A with only its most similar neighbor of B. Do the same in the other direction: Min: Final s(A, B) is the smaller of s. A(A, B) and s. B(A, B) [weakest link]

Computing Sim. Rank Rk(a, b) = estimate of Sim. Rank after k iterations. § Initialization: § Iteration: § Rk(a, b) is the similarity that has flowed a distance k away from the sources. Rk values are non-decreasing as k increases. We can prove that Rk(a, b) converges to s(a, b)

Time and Space Complexity Space complexity : O(n 2) to store Rk(a, b) Time complexity : O(kn 2 d 2), d 2 is the average of |I(a)||I(b)| over all vertex pairs (a, b) To improve performance, we can prune G 2: § Idea: vertices that are far apart should have very low similarity. We can approximate it as 0. § Select a radius r. If vertex-pair (a, b) cannot meet in less than r steps, remove it from the graph G 2. § space complexity: O(ndr) § time complexity: O(Kndrd 2), dr = avg. number of neighbors within radius r.

Random Surfer-Pairs Model Sim. Rank s(a, b) measures how soon two random surfers are expected to meet at the same node if they start at nodes a and b and randomly walk the graph backwards Background: Basic Forward Random Walk § Motion is in discrete steps, using edges of the graph. § Each time step, there is an equal probability of moving from your current vertex to one of your out-neighbors. § Given adjacency matrix A, the probability of walking from x to y is pxy = axy/O(x). Random Walk as a Markov Process § Initial location is described by the prob. distribution vector π(0) § Prob. of being at y at time 1:

Random Walk Transition Matrices Given adjacency matrix A: The forward and backward transition matrices:

Paired Backwards Random Walk Probability of walking backwards to x in one step: Two walkers meet at x if they start at a and b, and if one goes x a and the other goes x b, respectively. sx(a, b) = P(meeting at x) = π(a, b) p(x a) p(x b) s(a, b) = P(meeting) = Σx π(a, b) p(x a) p(x b) If they start together, they have met, so s(0)xy = 1 if i = j; 0 otherwise [identity matrix] Then

Experiments: Data Sets Two data sets § Research. Index (www. researchindex. com) a corpus of scientific research papers 688, 898 cross-reference among 278, 628 papers § Student’s transcripts 1030 undergraduate students in the School of Engineering at Stanford University Each transcript lists all course that the student has taken so far (average: 40 courses/student)

Performance Validation Metric Problem: Difficult to know what is the “correct” similarity between items. Solution: Define a rough domain-specific metric σ(p, q): § For scientific papers, we have two versions: σC(p, q) = fraction of q’s citations also cited by p σT(p, q) = fraction of words in q’s title also in p’s title § For university courses: σD(p, q) = 1 if p, q are in the same department, else 0

Computing the Performance Score Run the similarity algorithms: § Sim. Rank (naïve, pruned, minmax) § Co-Citation For each object p and algorithm A, form a set top. A, N(p) of the N objects most similar to p. For each q ∈ top. A, N(p), compute σ(p, q). Return the average σA, N(p) over all q.

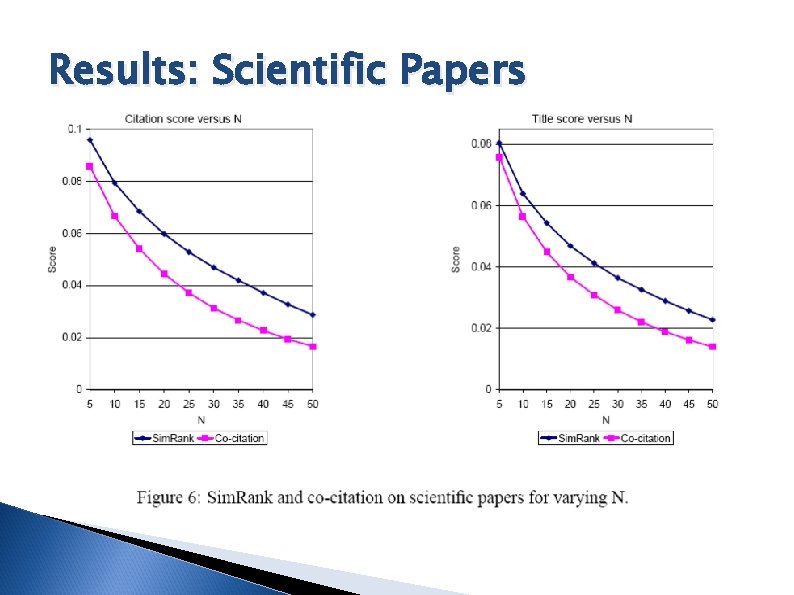
Experiment: Scientific Papers Setup § Used bipartite Sim. Rank, only considering inneighbors (validation uses out-neighbors) § N ∈ {5, 10, …, 45, 50} Results § Not very sensitive to decay factors C 1 and C 2 § Pruning the search radius had little effort on rank order of scores.

Results: Scientific Papers

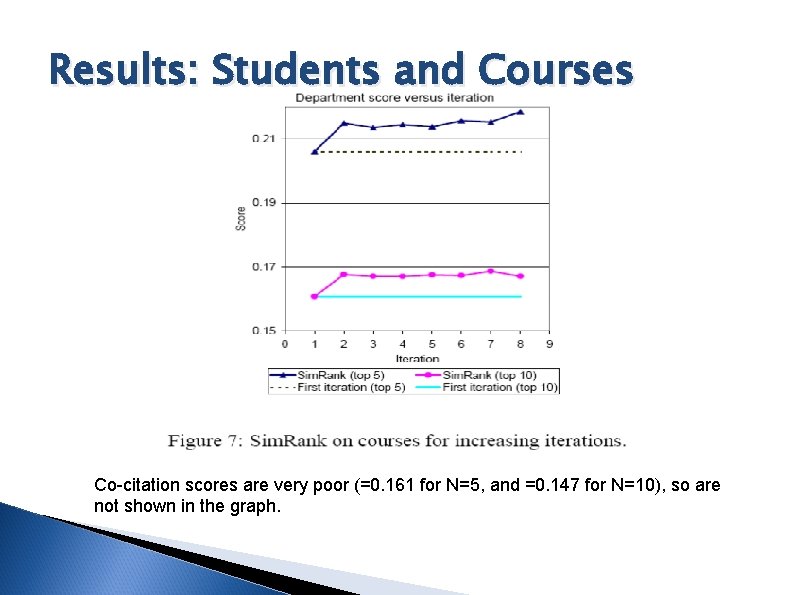
Experiment: Students and Courses Setup § Bipartite domain § N ∈ {5, 10} Results § Min-Max version of Sim. Rank performed the best § Not very sensitive to decay factors C 1 and C 2

Results: Students and Courses Co-citation scores are very poor (=0. 161 for N=5, and =0. 147 for N=10), so are not shown in the graph.

Conclusions Defined a recursive model of structural similarity between objects in a network Mathematically formulated Sim. Rank based on the recursive concept Presented a convergent algorithm to compute Sim. Rank Described a random-walk interpretation of Sim. Rank equations and scores Experimentally validated Sim. Rank over two real data sets

Open Issues and Critique O(n 2) is large; scalability needs to be improved. s(a, b) only includes contributions for paths when a and b are the same distance from some x. What if the distances are offset (total is odd)? As |I(a)| and |I(b)| increase, Sim. Rank decreases, even if I(a) = I(b)! § Addressed partially by Minimax method