Short course on spacetime modeling Instructors Peter Guttorp

Short course on space-time modeling Instructors: Peter Guttorp Johan Lindström Paul Sampson

Schedule 9: 10 – 9: 50 Lecture 1: Kriging 9: 50 – 10: 30 Lab 1 10: 30 – 11: 00 Coffee break 11: 00 – 11: 45 Lecture 2: Nonstationary covariances 11: 45 – 12: 30 Lecture 3: Gaussian Markov random fields 12: 30 – 13: 30 Lunch break 13: 30 – 14: 20 Lab 2 14: 20 – 15: 05 Lecture 4: Space-time modeling 15: 05 – 15: 30 Lecture 5: A case study 15: 30 – 15: 45 Coffee break 15: 45 – 16: 45 Lab 3

Kriging

The geostatistical model Gaussian process μ(s)=EZ(s) Var Z(s) < ∞ Z is strictly stationary if Z is weakly stationary if Z is isotropic if weakly stationary and

The problem Given observations at n locations Z(s 1), . . . , Z(sn) estimate Z(s 0) (the process at an unobserved location) or (an average of the process) In the environmental context often time series of observations at the locations.

Some history Regression (Bravais, Galton, Bartlett) Mining engineers (Krige 1951, Matheron, 60 s) Spatial models (Whittle, 1954) Forestry (Matérn, 1960) Objective analysis (Gandin, 1961) More recent work Cressie (1993), Stein (1999)

A Gaussian formula If then

Simple kriging Let X = (Z(s 1), . . . , Z(sn))T, Y = Z(s 0), so that μ X=μ 1 n, μ Y=μ, ΣXX=[C(si-sj)], ΣYY=C(0), and ΣYX=[C(si-s 0)]. Then This is the best unbiased linear predictor when μ and C are known (simple kriging). The prediction variance is

Some variants Ordinary kriging (unknown μ) where Universal kriging (μ(s)=A(s)β for some spatial variable A) where Still optimal for known C.

Universal kriging variance simple kriging variance variability due to estimating μ

The (semi)variogram Intrinsic stationarity Weaker assumption (C(0) needs not exist) Kriging predictions can be expressed in terms of the variogram instead of the covariance.

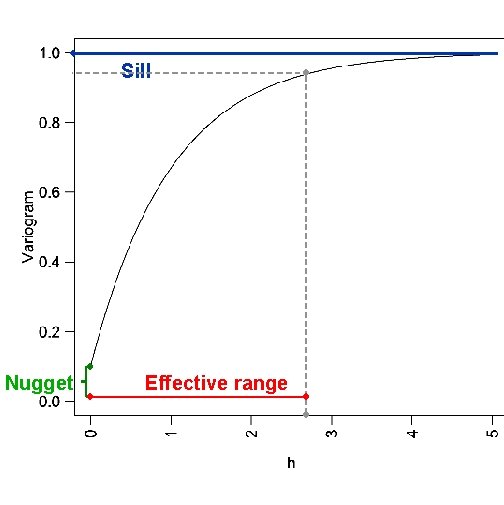
The exponential variogram A commonly used variogram function is γ (h) = σ2 (1 – e–h/ϕ). Corresponds to a Gaussian process with continuous but not differentiable sample paths. More generally, has a nugget τ2, corresponding to measurement error and spatial correlation at small distances.

Sill Nugget Effective range

Ordinary kriging where and kriging variance

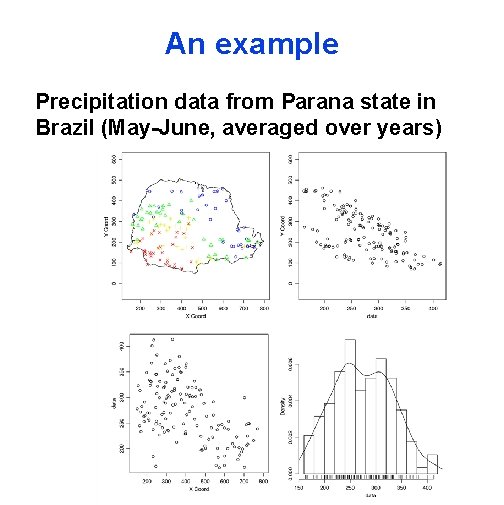
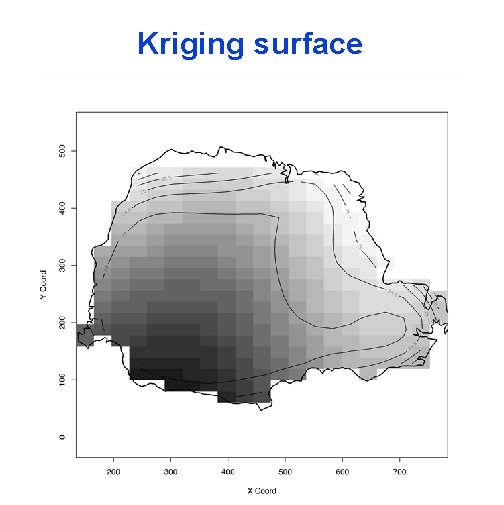
An example Precipitation data from Parana state in Brazil (May-June, averaged over years)

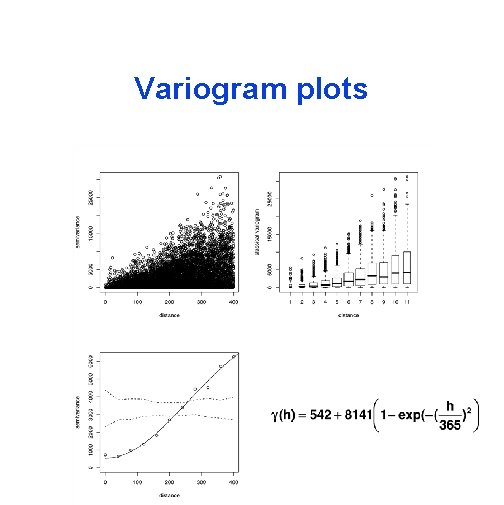
Variogram plots

Kriging surface

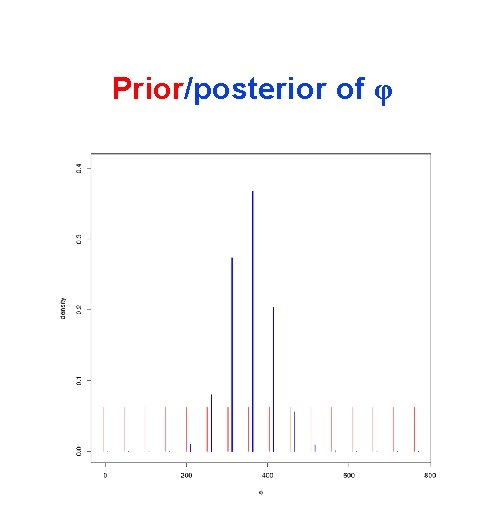
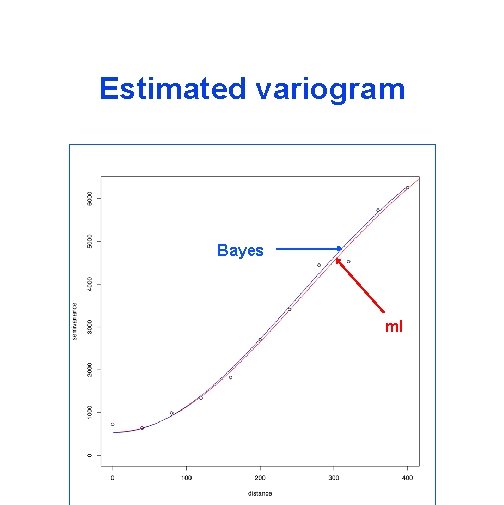
Bayesian kriging Instead of estimating the parameters, we put a prior distribution on them, and update the distribution using the data. Model: (Z(s 1). . . Z(sn))T θ=(β, σ 2, φ, τ 2) T Matrix with i, j-element C(si-sj; φ ) (correlation) measurement error

Prior/posterior of φ

Estimated variogram Bayes ml

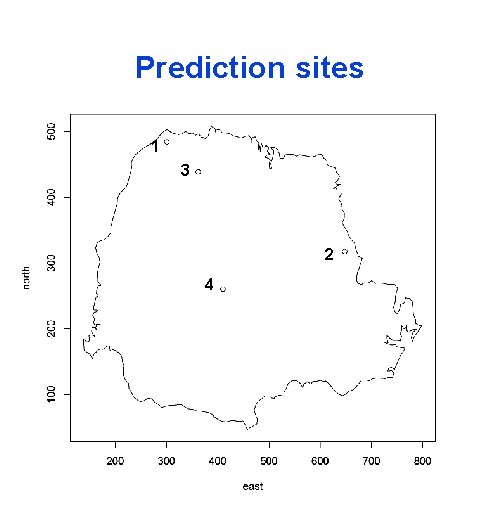
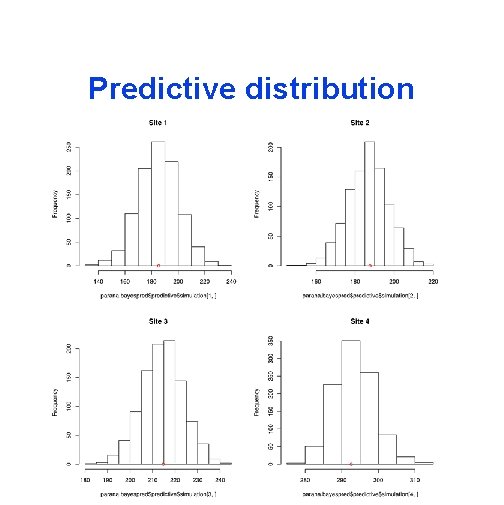
Prediction sites 1 3 2 4

Predictive distribution

References A. Gelfand, P. Diggle, M. Fuentes and P. Guttorp, eds. (2010): Handbook of Spatial Statistics. Section 2, Continuous Spatial Variation. Chapman & Hall/CRC Press. P. J. Diggle and Paulo Justiniano Ribeiro (2010): Model-based Geostatistics. Springer.