Stat 425 Introduction to Nonparametric Statistics Peter Guttorp

Stat 425 Introduction to Nonparametric Statistics Peter Guttorp NR and UW

Administrative issues Web page: http: //www. stat. washington. edu/pe ter/425/ Course grade based on participation (20%), homework (30%), midterm (25%) and final (25%). Both exams will be in class. Computing corner on Tuesdays. Homework due in class on Thursdays Office hour Tu 1 -2 CMU B 023

What the course is (and is not) about Parametric statistics: Data from a family of distributions described (indexed) by a parameter θ Under some conditions we can determine good statistical procedures (tests, estimates) How do you know if they are met? What if they are not met?

An example Test: t-test CI: Estimator: Assumptions:

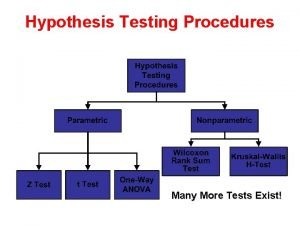
Topics 1. Checking distributional assumptions Empirical distribution function Kolmogorov-Smirnov statistic QQ-plot The importance of assumptions Shift function Density estimation Testing for independence

Topics, cont. 2. Ranks and order statistics When t-tests do not work Confidence sets for the median. Comparing the location of two or more distributions. Nonparametric approaches to bivariate data. Nonparametric Distribution-free

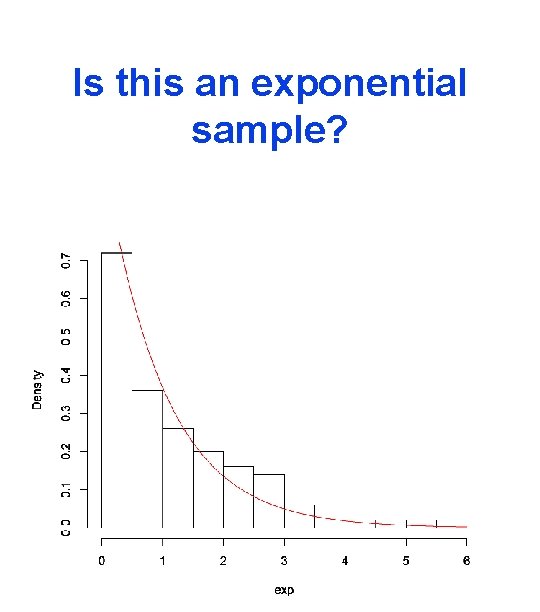
Is this an exponential sample?

The empirical distribution function For an event A, 1(A) = 1 if A happens, 0 otherwise. Let X 1, . . . , Xn be iid with distribution function (cdf) F(x). The empirical distribution function (edf) is defined as

Properties of edf 1. The edf is a cumulative distribution function. 2. It is an unbiased estimator of the true cdf. 3. It is consistent and asymptotically normal.

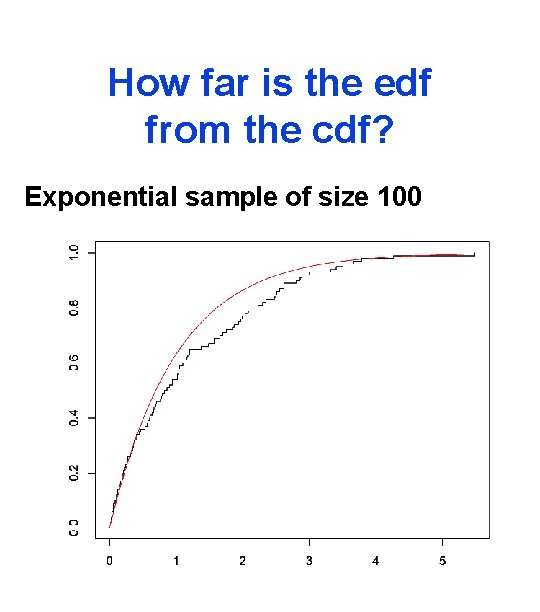
How far is the edf from the cdf? Exponential sample of size 100

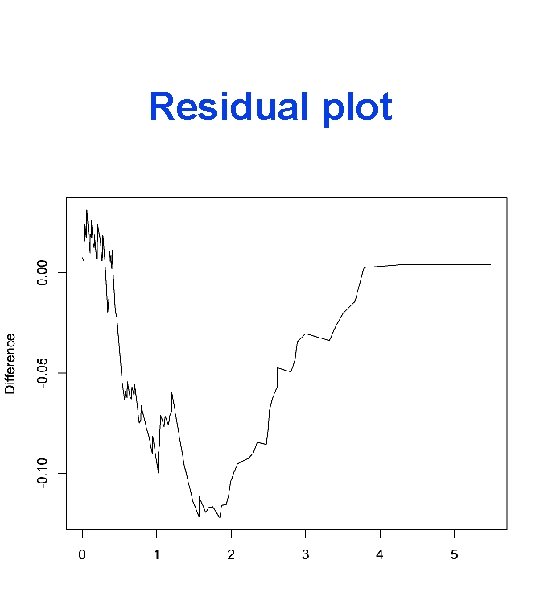
Residual plot

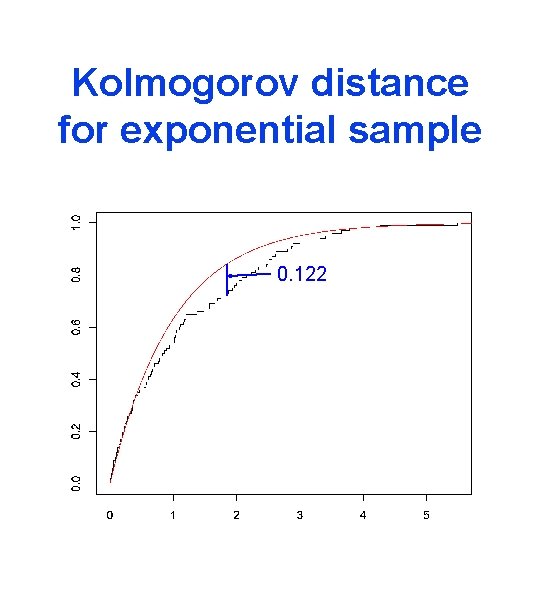
The Kolmogorov distance where x(1)<x(2)<. . . <x(n) is the ordered sample Another distance: Cramér-von Mises

Kolmogorov distance for exponential sample 0. 122

Why d. K does not depend on F 0 Considering transforming (monotonically) the x-axis. Does it change the distance? In particular, if X~F 0 what is the distribution of Y=F 0 (X)? Thus the distribution of d. K(Fn, F 0) is the same as the distribution of d. K(Gn, x) where Gn is the edf of a sample of size n from a uniform distribution on (0, 1) Distribution-free

The Kolmogorov. Smirnov test Let X~F. To test H 0: F = F 0 we (1) Estimate F by Fn (2) Calculate dn=d. K(Fn, F 0) (3) If dn is too large, reject H 0 One can also do a two-sample test, where X~F, Y~G and we test H 0: F = G by rejecting for large values of d. K(Fn, Gm).

Limiting distribution How large is large? It turns out that where This works for n ≥ 80; for smaller n there are tables and computer programs.

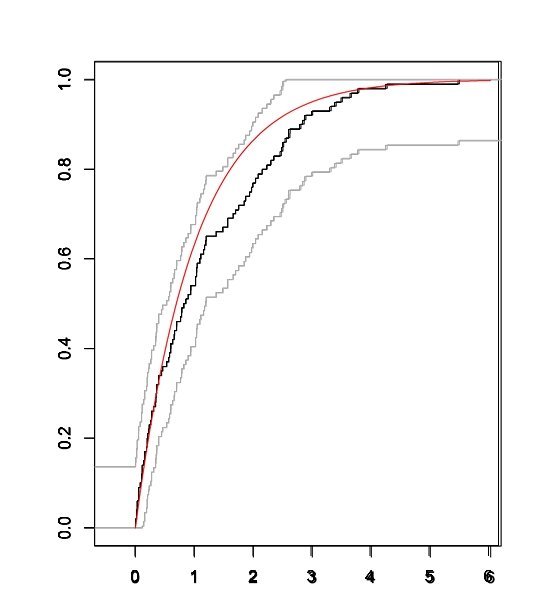
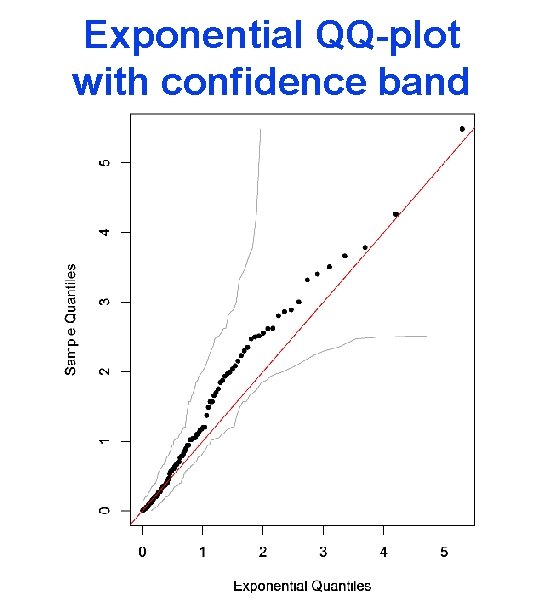
Confidence band for F For an unknown F, we use d. K(Fn, F) as a pivot: This confidence band is simultaneous (valid for all x) In particular, one can see if different candidate F fall inside the band.

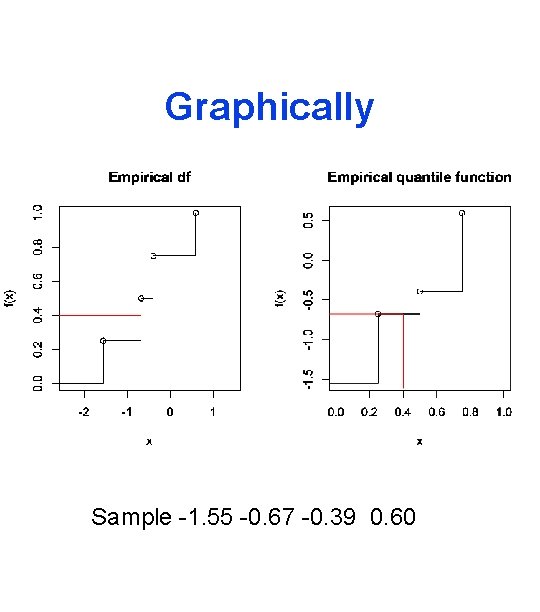
Quantile function For a continuous F there is a unique inverse function F-1. For a step function, like Fn, it is not unique, so we define the empirical quantile function as

Graphically Sample -1. 55 -0. 67 -0. 39 0. 60

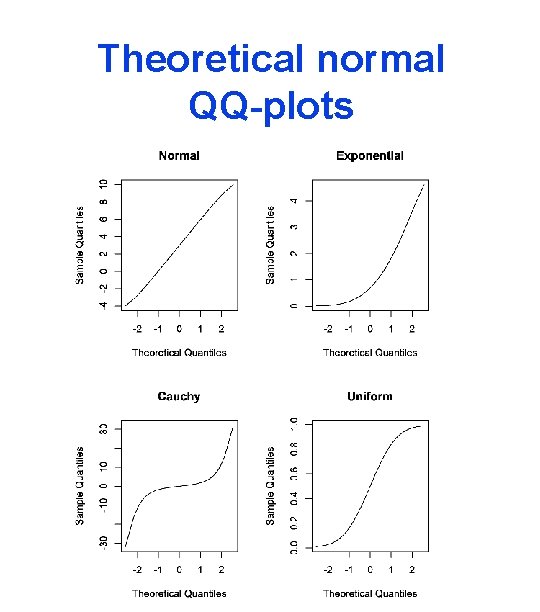
The q-q-plot The q-q plot is plotting (Fn-1(p), F 0 -1(p)) for p between 0 and 1 A common choice of F 0 is the normal distribution, but we can test any specified disytibution. We can get a simultaneous confidence band for F 0 -1, the same way we got it for the cdf.

Theoretical normal QQ-plots

Exponential QQ-plot with confidence band