Searching Also Logarithms Searching an array of integers

Searching Also: Logarithms

Searching an array of integers n If an array is not sorted, there is no better algorithm than linear search for finding an element in it static final int NONE = -1; // not a legal index static int linear. Search(int target, int[] a) { for (int p = 0; p < a. length; p++) { if (target == a[p]) return p; } return NONE; } 2

Searching an array of Strings n Searching an array of Strings is just like searching an array of integers, except n Instead of int 1==int 2 we need to use string 1. equals(string 2) static final int NONE = -1; // not a legal index static int linear. Search(String target, String[] a) { for (int p = 0; p < a. length; p++) { if (target. equals(a[p])) return p; } return NONE; } 3

Searching an array of Objects n Searching an array of Objects is just like searching an array of Strings, provided n The operation equals has been defined appropriately static final int NONE = -1; // not a legal index static int linear. Search(Object target, Object[] a) { for (int p = 0; p < a. length; p++) { if (target. equals(a[p])) return p; } return NONE; } 4

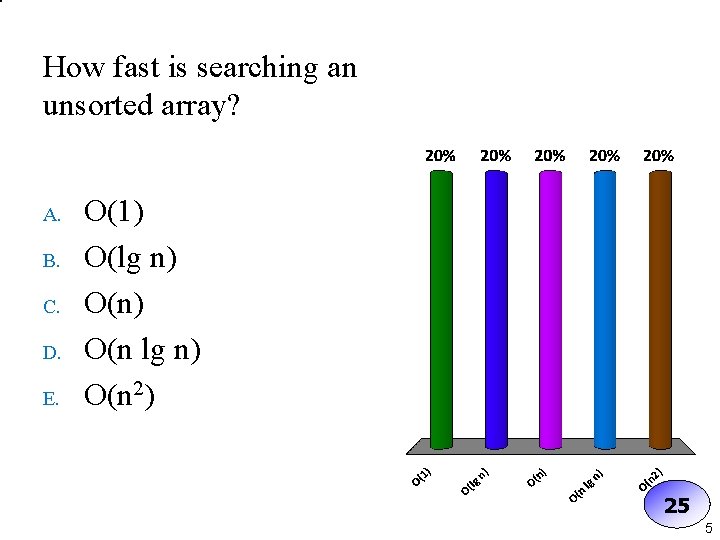
How fast is searching an unsorted array? A. B. C. D. E. O(1) O(lg n) O(n 2) 25 5

Templates n n There is no way, in Java, to write a general linear search method for any data type We can write a method that works for an array of objects (because Object defines the equals method) n n For arbitrary objects, equals is just == For your own objects, you may want to override public boolean equals(Object o) n n n The parameter must be of type Object! The method we defined for Objects also works fine for Strings (because String overrides equals) A search method for objects won’t work for primitives n Although an int can be autoboxed to an Integer, an int[] cannot be autoboxed to an Integer[] 6

Review: Overriding methods n n To override a method means to replace an inherited method with one of your own Your new method must be a legal replacement for the inherited version n Consequences: n n n Your new method must have the exact same signature (name, order and types of parameters—but parameter names are irrelevant) Your new method must have the same return type Your new method must be at least as public as the method it replaces Your new method can throw no new exceptions that the method being overridden doesn’t already throw In Java 5 and later, you should put @Override in front of your method n This lets the compiler check that you got the signature right 7

Java review: equals n n n The Object class defines public boolean equals(Object obj) For most objects, this just tests identity: whether the two objects are really one and the same This is not generally what you want The String class overrides this method with a method that is more appropriate for Strings You can override equals for your own classes n If you override equals, there are some rules you should follow 8

Overriding equals n If you override equals, your method should have the following properties (for your objects x, y, z) n n Reflexive: for any x, x. equals(x) should return true Symmetric: for any non-null objects x and y, x. equals(y) should return the same result as y. equals(x) n n For any non-null x, x. equals(null) should return false Transitive: if x. equals(y) and y. equals(z) are true, then x. equals(z) should also be true Consistent: x. equals(y) should always return the same answer (unless you modify x or y, of course) Java cannot check to make sure you follow these rules 9

Reference implementation for equals n public class Person { String name; public Person(String name) { this. name = name; } @Override public boolean equals(Object o) { if (this == o) return true; if (! (o instanceof Person)) return false; Person p = (Person)o; return (name. equals(p. name)); } } 10

public static void main(String[] args) { Person john = new Person("John"); Person jack = new Person("John"); System. out. println(jack. equals(john)); System. out. println(jack == john); } What gets printed? A. B. C. D. false then true then false true then true 25 11

About sorted arrays n n An array is sorted in ascending order if each element is no smaller than the preceding element An array is sorted in descending order if each element is no larger than the preceding element When we just say an array is “sorted, ” by default we mean that it is sorted in ascending order An array of Object cannot be in sorted order ! n n There is no notion of “smaller” or “larger” for arbitrary objects We can define an ordering for some of our objects 12

The Comparable interface n java. lang provides a Comparable interface with the following method: n n public int compare. To(Object that) This method should return n n A negative integer if this is less than that Zero if this equals that A positive integer if this is greater than that Reminder: you implement an interface like this: class My. Object implements Comparable { public int compare. To(Object that) {. . . } } 13

Rules for implementing Comparable n You must ensure: n n n x. compare. To(y) and y. compare. To(x) either are both zero, or else one is positive and the other is negative x. compare. To(y) throws an exception if and only if y. compare. To(x) throws an exception The relation is transitive: (x. compare. To(y)>0 && y. compare. To(z)>0) implies x. compare. To(z)>0 if x. compare. To(y)==0, then x. compare. To(z) has the same sign as y. compare. To(z) You should ensure: n compare. To is consistent with equals 14

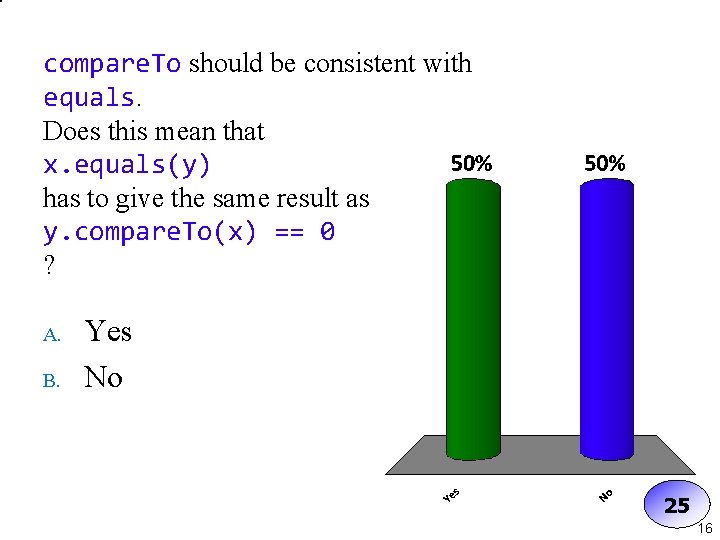
Consistency with equals n compare. To is consistent with equals if: x. compare. To(y)==0 gives the same boolean result as x. equals(y) n n Therefore: if you implement Comparable, you really should override equals as well Java doesn’t actually require consistency with equals, but sooner or later you’ll get into trouble if you don’t meet this condition 15

compare. To should be consistent with equals. Does this mean that x. equals(y) has to give the same result as y. compare. To(x) == 0 ? A. B. Yes No 25 16

Binary search n Linear search has linear time complexity: n n Time n if the item is not found Time n/2, on average, if the item is found If the array is sorted, we can write a faster search How do we look up a name in a phone book, or a word in a dictionary? n n n Look somewhere in the middle Compare what’s there with the thing you’re looking for Decide which half of the remaining entries to look at Repeat until you find the correct place This is the binary search algorithm 17

Binary search algorithm (p. 43) n To find which (if any) component of a[left. . right] is equal to target (where a is sorted): Set l = left, and set r = right While l <= r, repeat: Let m be an integer about midway between l and r If target is equal to a[m], terminate with answer m If target is less than a[m], set r = m– 1 If target is greater than a[m], set l = m+1 Terminate with answer none l • • • m-1 m m+1 ? r • • • 18

Example of binary search Search the following array a for 36: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 a 5 7 10 13 13 15 19 19 23 28 28 32 32 37 41 46 1. (0+15)/2=7; a[7]=19; too small; search 8. . 15 2. (8+15)/2=11; a[11]=32; too small; search 12. . 15 3. (12+15)/2=13; a[13]=37; too large; search 12. . 12 4. (12+12)/2=12; a[12]=32; too small; search 13. . 12. . . but 13>12, so quit: 36 not found 19

Binary search in Java (p. 45) static int binary. Search(Comparable target, Comparable[] a, int left, int right) { int l = left, r = right; while (l <= r) { int m = (l + r) / 2; int comp = target. compare. To(a[m]); if (comp == 0) return m; else if (comp < 0) r = m – 1; else /* comp > 0 */ l = m + 1; } return NONE; // As before, NONE = -1 } 20

Recursive binary search in Java static int binary. Search(Comparable target, Comparable[] a, int left, int right) { if (left > right) return NONE; int m = (left + right) / 2; int comp = target. compare. To(a[m]); if (comp == 0) return m; else if (comp < 0) return binary. Search(target, a, left, m-1); else { assert comp > 0; return binary. Search(target, a, m+1, right); } } 21

How fast is binary searching a sorted array? A. B. C. D. E. O(1) O(lg n) O(n 2) 25 22

Strings of bits n n n There is only one possible zero-length sequence of bits There are two possible “sequences” of a single bit: 0, 1 There are four sequences of two bits: 00 01, 10 11 There are eight sequences of three bits: 000 001, 010 011, 100 101, 110 111 Each time you add a bit, you double the number of possible sequences n n Add 0 to the end of each existing sequence, and do the same for 1 “Taking the logarithm” is the inverse of exponentiation 20 = 1 21 = 2 22 = 4 23 = 8, etc. log 21 = 0 log 22 = 1 log 24 = 2 log 28 = 3, etc. 23

Logarithms n n In computer science, we almost always work with logarithms base 2, because we work with bits log 2 n (or we can just write log n) tells us how many bits we need to represent n possibilities n n n Example: To represent 10 digits, we need log 10 = 3. 322 bits Since we can’t have fractional bits, we need 4 bits, with some bit patterns not used: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, and not 1010, 1011, 1100, 1101, 1110, 1111 Logarithms also tell us how many times we can cut a positive integer in half before reaching 1 n n Example: 16/2=8, 8/2=4, 4/2=2, 2/2=1, and log 16 = 4 Example: 10/2=5, 5/2=2. 5, 2. 5/2=1. 25, and log 10 = 3. 322 24

Relationships n n n n n Logarithms of the same number to different bases differ by a constant factor log 2(2) = 1. 000 log 2(3) = 1. 585 log 2(4) = 2. 000 log 2(5) = 2. 322 log 2(6) = 2. 585 log 2(7) = 2. 807 log 2(8) = 3. 000 log 2(9) = 3. 170 log 2(10)= 3. 322 log 10(2) = 0. 301 log 10(3) = 0. 477 log 10(4) = 0. 602 log 10(5) = 0. 699 log 10(6) = 0. 778 log 10(7) = 0. 845 log 10(8) = 0. 903 log 10(9) = 0. 954 log 10(10) = 1. 000 log 2(2)/log 10(2) = 3. 322 log 2(3)/log 10(3) = 3. 322 log 2(4)/log 10(4) = 3. 322 log 2(5)/log 10(5) = 3. 322 log 2(6)/log 10(6) = 3. 322 log 2(7)/log 10(7) = 3. 322 log 2(8)/log 10(8) = 3. 322 log 2(9)/log 10(9) = 3. 322 log 2(10)/log 10(10)= 3. 322 25

Logarithms—a summary n Logarithms are exponents n n n n if bx = a, then logba = x if 103 = 1000, then log 101000 = 3 if 28 = 256, then log 2256 = 8 If we start with x=1 and multiply x by 2 eight times, we get 256 If we start with x=256 and divide x by 2 eight times, we get 1 log 2 is how many times we halve a number to get 1 log 2 is the number of bits required to represent a number in binary (fractions are rounded up) Your textbook uses lg to mean log 2 26

Binary search takes log n time n n n In binary search, we choose an index that cuts the remaining portion of the array in half We repeat this until we either find the value we are looking for, or we reach a subarray of size 1 If we start with an array of size n, we can cut it in half log 2 n times Hence, binary search has logarithmic (log n) time complexity For an array of size 1000, this is 100 times faster than linear search (210 ~= 1000) 27

Conclusion n Linear search has linear time complexity Binary search has logarithmic time complexity For large arrays, binary search is far more efficient than linear search n n However, binary search requires that the array be sorted If the array is sorted, binary search is n n n 100 times faster for an array of size 1000 50 000 times faster for an array of size 1 000 This is the kind of speedup that we care about when we analyze algorithms 28

The End 29