Natural Logarithms Natural Logs ande Start by graphing

Natural Logarithms

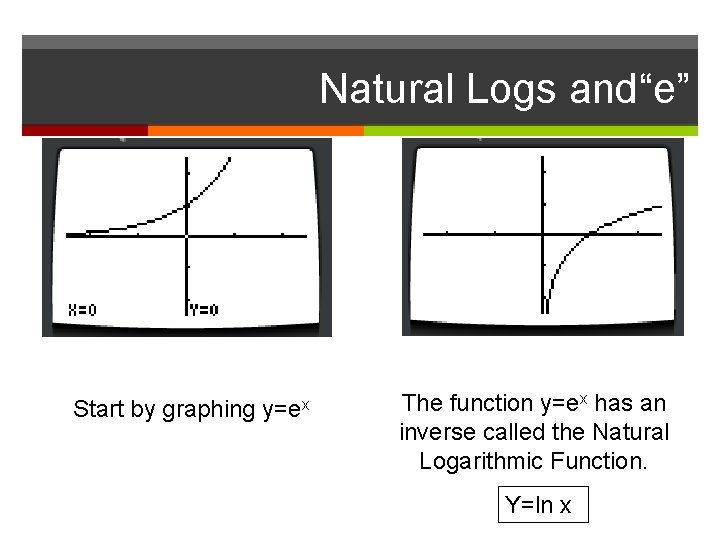
Natural Logs and“e” Start by graphing y=ex The function y=ex has an inverse called the Natural Logarithmic Function. Y=ln x

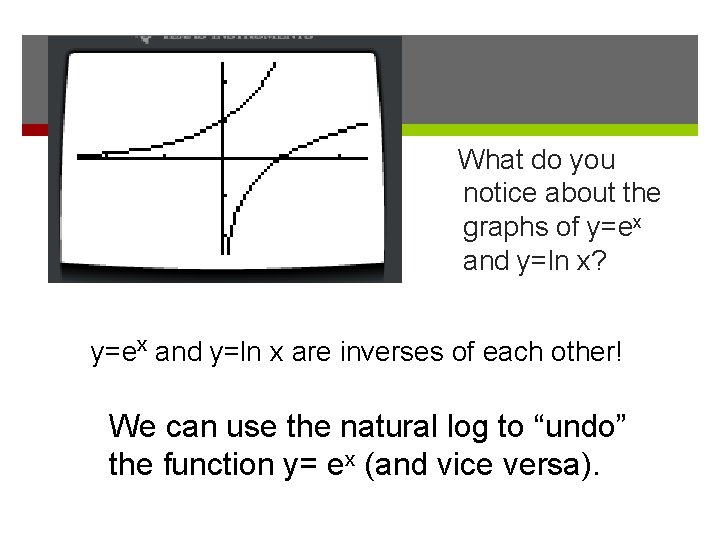
What do you notice about the graphs of y=ex and y=ln x? y=ex and y=ln x are inverses of each other! We can use the natural log to “undo” the function y= ex (and vice versa).

All the rules still apply You can use your product, power and quotient rules for natural logs just like you do for regular logs Let’s try one:

Solving with base “e” 1. Subtract 2. 5 from both sides 2. Divide both sides by 7 3. Take the natural log of both sides. 4. Simplify. 5. Divide both sides by 2 x = 0. 458 6. Calculator

Another Example: Solving with base “e” 1. Take the natural log of both sides. 2. Simplify. 3. Subtract 1 from both sides x = 2. 401 4. Calculator

Solving a Natural Log problem To “undo” a natural log, we use “e” 1. Rewrite in exponential form 2. Use a calculator 3. Simplify.

Another Example: Solving Natural Logs 1. Rewrite in exponential form. 2. Calculator. 3. Take the square root of each time 3 x+5 = 7. 39 or -7. 39 X=0. 797 or -4. 130 4. Calculator 5. Simplify

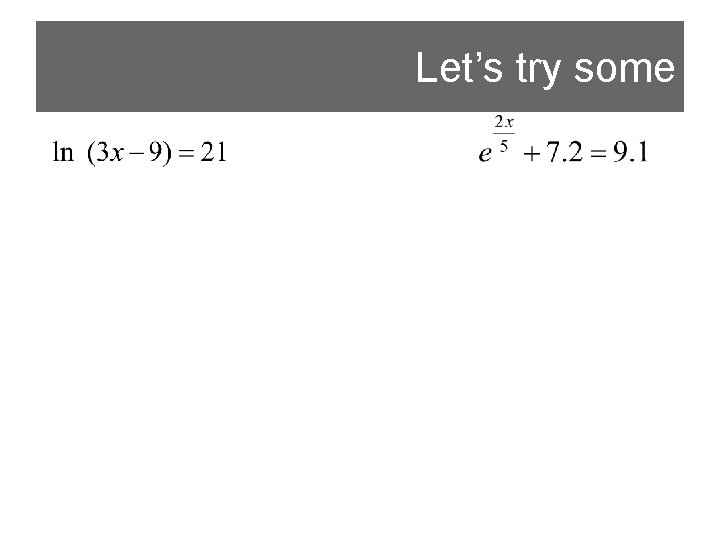
Let’s try some

Let’s try some

Going back to our continuously compounding interest problems. . . A $20, 000 investment appreciates 10% each year. How long until the stock is worth $50, 000? Remember our base formula is A = Pert. . . We now have the ability to solve for t A = $50, 000 (how much the car will be worth after the depreciation) P = $20, 000 (initial value) r = 0. 10 t = time From what we have learned, try solving for time

Going back to our continuously compounding interest problems. . . $20, 000 appreciates 10% each year. How long until the stock is worth $50, 000? A = $50, 000 (how much the car will be worth after the depreciation) P = $20, 000 (initial value) r = 0. 10 t = time

Special Thanks to: Pleasanton, CA Public Schools www. pleasanton. k 12. ca. us/. . . /Powerpoints/. . . /8. 6% 20 Natural%. . .