Risk and Return and the Capital Asset Pricing


















![Risk-free borrowing and lending o o o Consider combinations of E[R] the risk-free asset Risk-free borrowing and lending o o o Consider combinations of E[R] the risk-free asset](https://slidetodoc.com/presentation_image_h/81891f5e12d0004ee2bf2c2e1791f0cd/image-28.jpg)




- Slides: 35

Risk and Return and the Capital Asset Pricing Model (CAPM) For 9. 220, Chapter

Risk Return & The Capital Asset Pricing Model (CAPM) l l l To make “good” (i. e. , value-maximizing) financial decisions, one must understands the relationship between risk and return We accept the notion that rational investors like returns and dislike risk Consider the following proxies for return and risk: Expected return - weighted average of the distribution of possible returns in the future. Variance of returns - a measure of the dispersion of the distribution of possible returns in the future.

Expected (Ex Ante) Return where, Ri = the return in state i (there are S states) Pi = the probability of return i (state i) An Example Consider the following return figures for the following year on stock XYZ under three alternative states of the economy Pi Ri Probability Return in State of Economy of state i +1% change in GNP 0. 25 -5% +2% change in GNP 0. 50 15% +3% change in GNP 0. 25 35%

Expected Returns - An Example Q. Calculate the expected return on stock XYZ for the next year Use the following table A. Pi State of Economy Probability of state i R i Pi R i Return in state i State 1: +1% change in GNP 0. 25 -5% - 1. 25% State 2: +2% change in GNP 0. 50 15% 7. 50% State 3: +3% change in GNP 0. 25 35% 8. 75% Expected Return=15. 00% Or, use the formula:

Variance and Standard Deviation of Returns where, and Ri = the return in state i (there are S states) Pi = the probability of return i (state i) s = the standard deviation of the return: An Example Recall the return figures for the following year on stock XYZ under three alternative states of the economy Pi Ri Probability of state i Return in state i State 1: +1% change in GNP 0. 25 -5% State 2: +2% change in GNP 0. 50 15% State 3: +3% change in GNP 0. 25 35% State of Economy Expected Return = 15. 00%

Variance & Standard Deviation - An Example Q. Calculate the variance and standard deviation of returns on stock XYZ A. Use the following table Pi X (Ri - E[R])2. = Pi(Ri - E[R])2 State of Economy Probability of state i +1% change in GNP 0. 25 0. 04 0. 01 +2% change in GNP 0. 50 0. 00 +3% change in GNP 0. 25 0. 04 0. 01 Variance of Return =0. 02 Or, use the formula: Standard deviation:

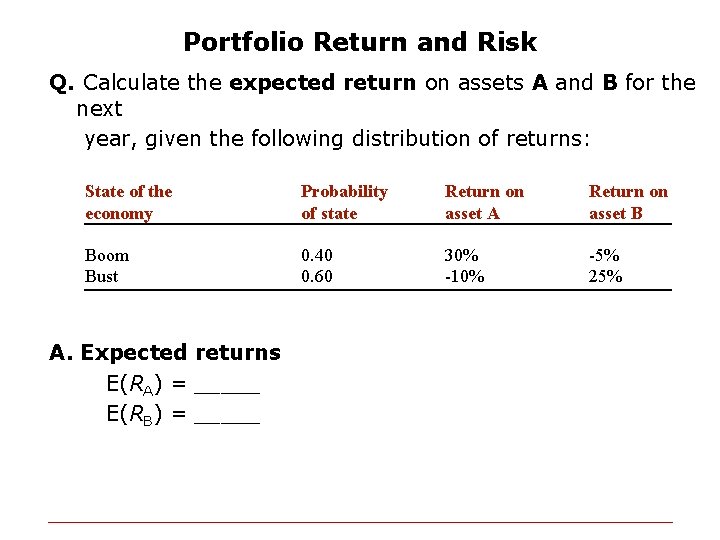
Portfolio Return and Risk Q. Calculate the expected return on assets A and B for the next year, given the following distribution of returns: State of the economy Probability of state Return on asset A Return on asset B Boom Bust 0. 40 0. 60 30% -10% -5% 25% A. Expected returns E(RA) = _____ E(RB) = _____

Q. Calculate the variance of the above assets A and B A. Variances Var(RA) = ____ Var(RB) = _____ Q. Calculate the standard deviations of the above assets A and B A. Standard Deviations s. A = ____ s. B = ____

Returns and Risk for Portfolios - 2 Assets Expected Return on a Portfolio The Expected Return on Portfolio p with N securities where, E[Ri]= expected return of security i Xi = proportion of portfolio's initial value invested in security i Example Consider a portfolio p with 2 assets: 50% invested in asset A and 50% invested in asset B. The Portfolio expected return is given by: E(RP) = XAE(RA) + XBE(RB) = (0. 50 x 0. 06) + (0. 50 x 0. 13) = 0. 095 = 9. 5%

Variance of a Portfolio The variance of portfolio p with two assets (A and B) where, Standard Deviation of a Portfolio The standard deviation of portfolio p with two assets (A and B)

Q. Calculate the variance of portfolio p (50% in A and 50% in B) A. Recall: Var(RA) = 0. 0384, and Var(RB) = 0. 0216 First, we need to calculate the covariance b/w A and B: = 0. 40 x(0. 30 -0. 06)(-0. 05 -0. 13) + 0. 60 x(-0. 10 -0. 06)(0. 250. 13) = - 0. 0288 The variance of portfolio p Q. Calculate the standard deviations of portfolio p A. Standard Deviations p = (0. 0006)1/2 = 0. 0245 = 2. 45%

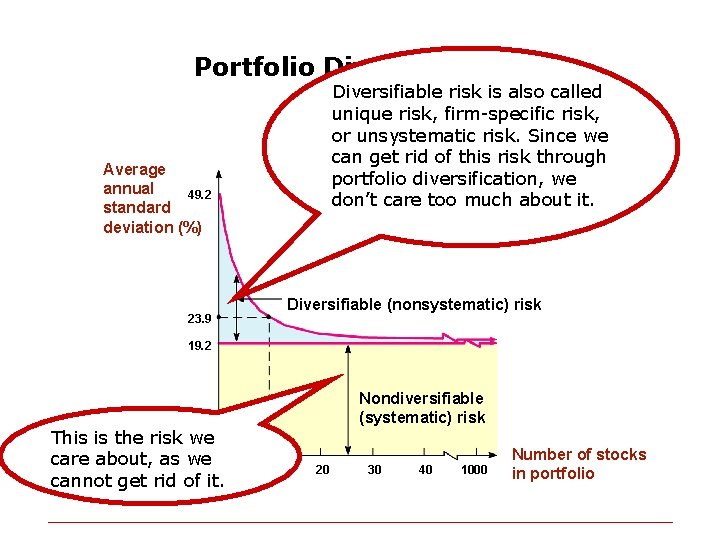
The Effect of Diversification on Portfolio Risk Note: u E(RP) = XAE(RA) + XBE(RB) = 9. 5%, but u u Var(Rp) =0. 0006 < XAVar(RA) + XBVar(RB) = (0. 50 x 0. 0384) + (0. 50 x 0. 0216) = 0. 03 This means that by combining assets A and B into portfolio p, we eliminate some risk (mainly due to the covariance term) Diversification - Strategy designed to reduce risk by spreading the portfolio across many investments Two types of Risk: Unsystematic/unique/asset-specific risks - can be diversified away Systematic or “market” risks - can’t be diversified away u In general, a well diversified portfolio can be created by randomly combining 25 risky securities into a portfolio (with little (no) cost).

Portfolio Diversification Diversifiable risk is also called unique risk, firm-specific risk, or unsystematic risk. Since we can get rid of this risk through portfolio diversification, we don’t care too much about it. Average annual 49. 2 standard deviation (%) Diversifiable (nonsystematic) risk 23. 9 19. 2 This is the risk we care about, as we 1 cannot get rid of it. Nondiversifiable (systematic) risk 10 20 30 40 1000 Number of stocks in portfolio

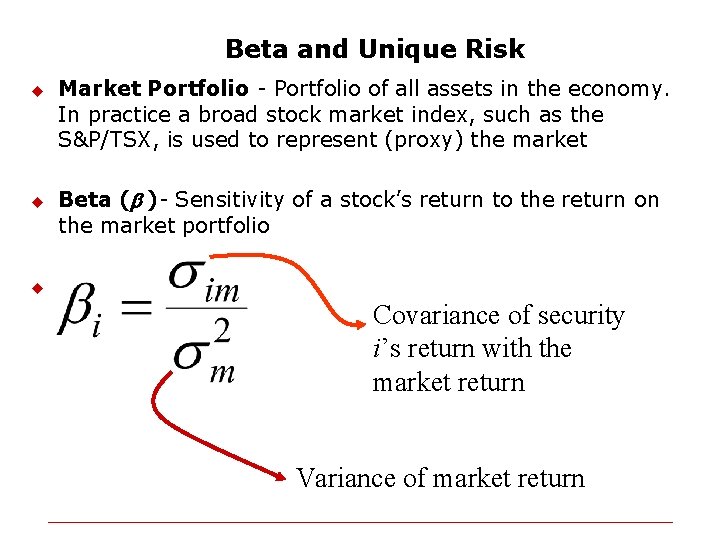
Beta and Unique Risk u u u Total risk = diversifiable risk + market risk We assume that diversification is costless, thus diversifiable (nonsystematic) risk is irrelevant Investors should only care about non-diversifiable (systematic) market risk Market risk is measured by beta - the sensitivity to market changes Example: Return (%) State of the economy Good Poor TSE 300 18 6 BCE 26 -4

Beta and Market Risk The Characteristic Line • (26%, 18%) Slope = b = 2. 5 • (-4%, 6%) Interpretation: Following a change of +1% (-1%) in the market return, the return on BCE will change by +2. 5% (-2. 5%) NOTE: If the security has a -ve cov w/ TSE 300 =>

Beta and Unique Risk u u Market Portfolio - Portfolio of all assets in the economy. In practice a broad stock market index, such as the S&P/TSX, is used to represent (proxy) the market Beta (b )- Sensitivity of a stock’s return to the return on the market portfolio u Covariance of security i’s return with the market return Variance of market return

Markowitz Portfolio Theory u u We saw that combining stocks into portfolios can reduce standard deviation Covariance, or the correlation coefficient, make this possible: The standard deviation of portfolio p (with XA in A and XB in B): Note: Thus, , or

Markowitz Portfolio Theory - An Example u u Consider assets Y and Z, with Consider portfolio p consisting of both Y and X. Then, we have: Expected Return of p Standard Deviation of p

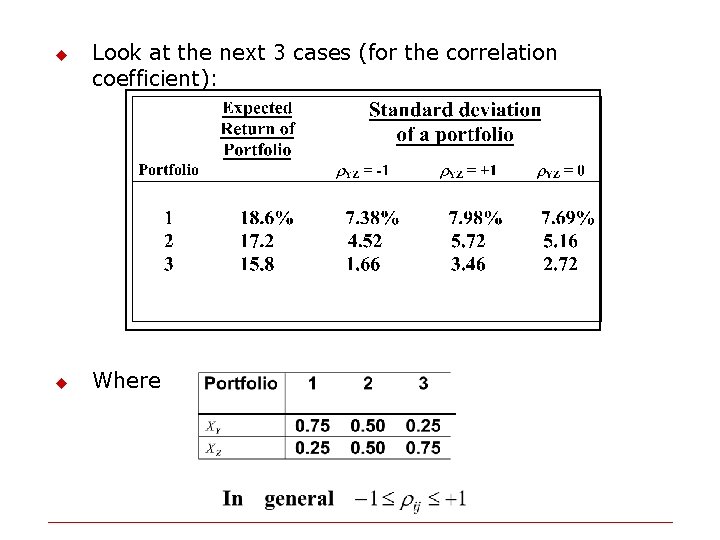
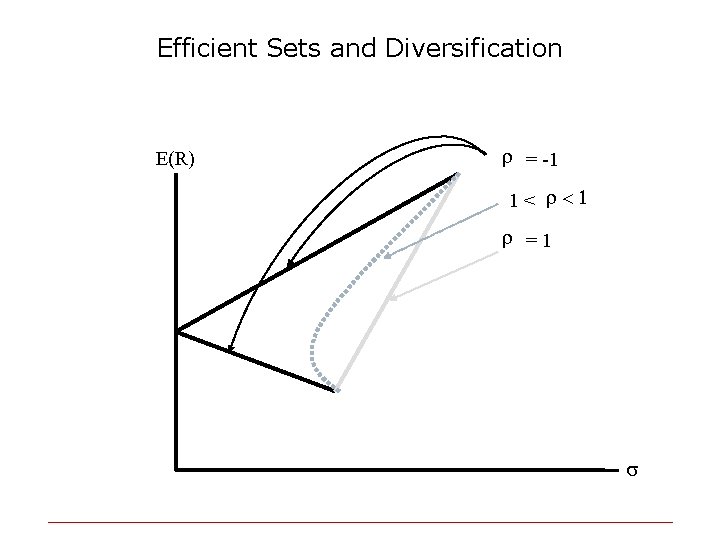
u u Look at the next 3 cases (for the correlation coefficient): Where

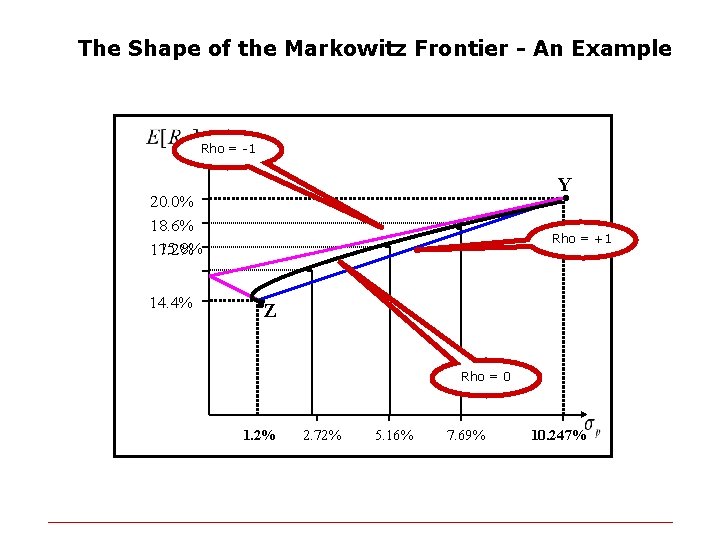
The Shape of the Markowitz Frontier - An Example Rho = -1 20. 0% 18. 6% 15. 8% 17. 2% 14. 4% . . . Y Rho = +1 Z Rho = 0 1. 2% 2. 72% 5. 16% 7. 69% 10. 247%

Efficient Sets and Diversification E(R) r = -1 -1 < r < 1 r =1 s

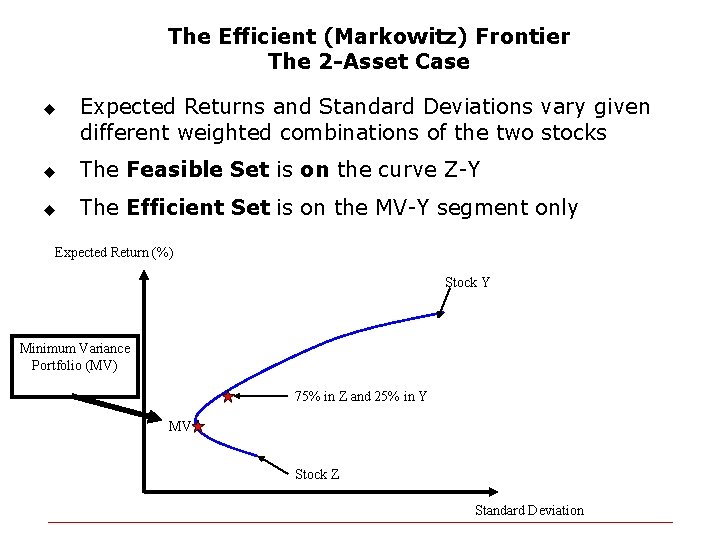
The Efficient (Markowitz) Frontier The 2 -Asset Case u Expected Returns and Standard Deviations vary given different weighted combinations of the two stocks u The Feasible Set is on the curve Z-Y u The Efficient Set is on the MV-Y segment only Expected Return (%) Stock Y Minimum Variance Portfolio (MV) 75% in Z and 25% in Y MV Stock Z Standard Deviation

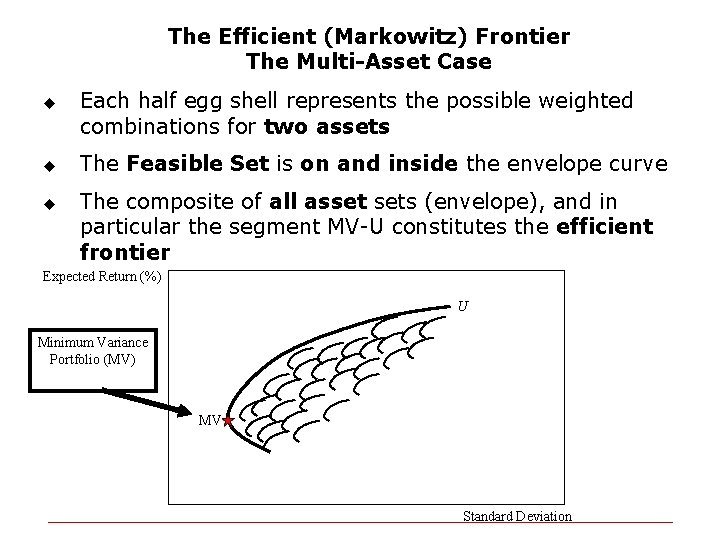
The Efficient (Markowitz) Frontier The Multi-Asset Case u u u Each half egg shell represents the possible weighted combinations for two assets The Feasible Set is on and inside the envelope curve The composite of all asset sets (envelope), and in particular the segment MV-U constitutes the efficient frontier Expected Return (%) U Minimum Variance Portfolio (MV) MV Standard Deviation

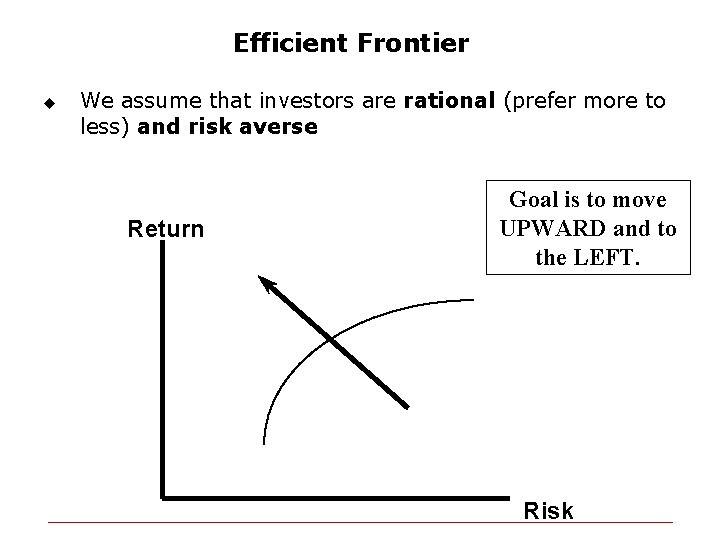
Efficient Frontier u We assume that investors are rational (prefer more to less) and risk averse Return Goal is to move UPWARD and to the LEFT. Risk

Which Asset Dominates? Return Low Risk High Return Low Risk High Risk Low Return Risk

Short Selling u Definition The sale of a security that the investor does not own. u How? Borrow the security from your broker and sell it in the open market. u Cash Flow At the initiation of the short sell, your only cash flow, is the proceeds from selling the security. u Closing the Short Eventually you will have to buy the security back in order to return it to the broker. u Cash Flow At the elimination of the short sell, your only cash flow, is the price you have to pay for the security in the open market.

Short Selling A Treasury Bill - An Example u The Security -- A Treasury bill is a zero-coupon bond issued by the Government, with a face value of $100, and with a maturity no longer than one year. If the yield on a 1 -year T-bill is 5%, then its current price is: 100/1. 051 = $95. 24 u The Short sell -- Borrow the 1 -year T-bill from your broker and sell it in the open market for $95. 24. u u Closing the Short -- At the end of the year - buy the T-bill back (an instant before it matures) in order to return it to the broker u u Cash Flow-- The short sell proceeds: $95. 24 Cash Flow -- The price you have to pay for the T-bill in the open market an instant before maturity (in 1 year): 100/1. 050 = $100 Risk-Free Borrowing -- This transaction is equivalent to borrowing $95. 24 for one year, and paying back $ 100 in a year. The interest rate is: (100/95. 24) -1 = 5% = the 1 -year T-bill yield
![Riskfree borrowing and lending o o o Consider combinations of ER the riskfree asset Risk-free borrowing and lending o o o Consider combinations of E[R] the risk-free asset](https://slidetodoc.com/presentation_image_h/81891f5e12d0004ee2bf2c2e1791f0cd/image-28.jpg)
Risk-free borrowing and lending o o o Consider combinations of E[R] the risk-free asset with a portfolio, Z, on the Efficient Frontier. With a risk-free asset available, taking a long f position (positive portfolio weight in f) Rf gives us risk-free lending combined with A. Taking a short f position (negative portfolio weight in f) gives us risk-free borrowing combined with A. Portfolio Z n wi ro r Bo A+ n e +L g n di A P g

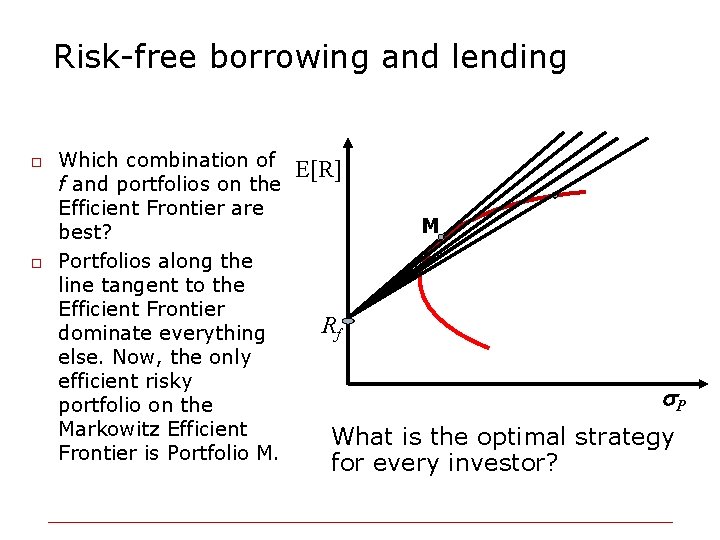
Risk-free borrowing and lending o o Which combination of f and portfolios on the Efficient Frontier are best? Portfolios along the line tangent to the Efficient Frontier dominate everything else. Now, the only efficient risky portfolio on the Markowitz Efficient Frontier is Portfolio M. E[R] M Rf P What is the optimal strategy for every investor?

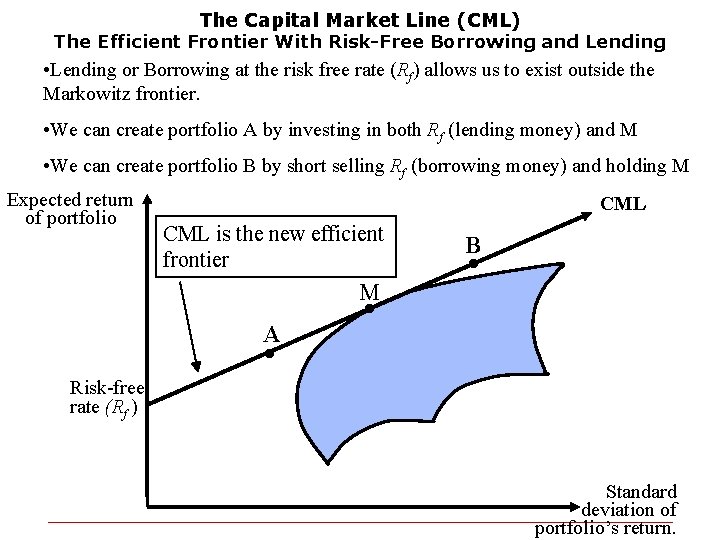
The Capital Market Line (CML) The Efficient Frontier With Risk-Free Borrowing and Lending • Lending or Borrowing at the risk free rate (Rf) allows us to exist outside the Markowitz frontier. • We can create portfolio A by investing in both Rf (lending money) and M • We can create portfolio B by short selling Rf (borrowing money) and holding M Expected return of portfolio CML is the new efficient frontier . A . M . CML B Risk-free rate (Rf ) Standard deviation of portfolio’s return.

The Capital Asset Pricing Model (CAPM) Note u all securities are in M, and u all investors have M in their portfolios since they are all on the new efficient frontier - CLM - investing in Rf and M. Therefore Investors are only concerned with and , and with the contribution of each security i to M, in terms of u contribution of systematic risk (measured by beta) u contribution of expected return According to the CAPM: where,

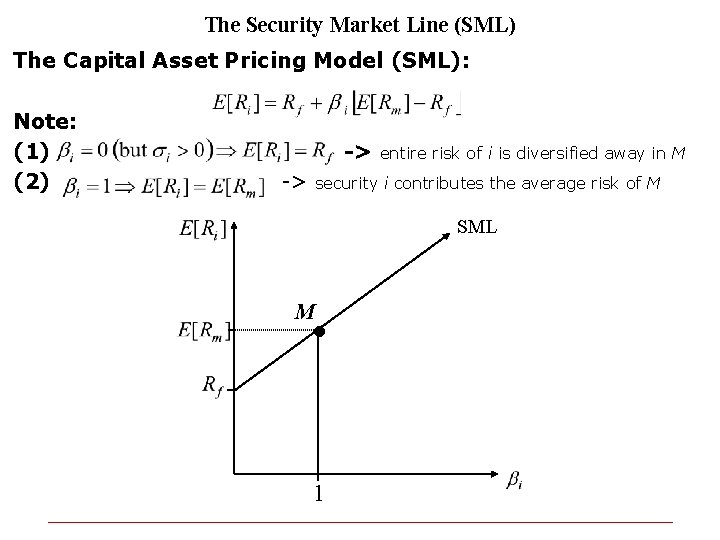
The Security Market Line (SML) The Capital Asset Pricing Model (SML): Note: (1) (2) -> -> entire risk of i is diversified away in M security i contributes the average risk of M SML . M 1

The Security Market Line (SML) u The SML is always linear u CML - just for efficient portfolios u SML - for any security and portfolio (efficient or inefficient)

The Security Market Line (SML) Example: Consider stocks A and B, with: ba = 0. 8, bb = 1. 2, let E[Rm] = 14% and Rf = 4%. By the SML: E[Ra] = 4% + 0. 8[14% - 4%] = 12% E[Rb] = 4% + 1. 2[14% - 4%] = 16% Consider a portfolio p, with 60% invested in A and 40% invested in B, then: E[Rp] = Xa. E[Ra] + Xb. E[Rb] = 0. 6 x 12% + 0. 4 x 16% = 13. 6% And, bp = Xa ba + Xb bb = 0. 6 x 0. 8 + 0. 4 x 1. 2 = 0. 96 By the CAPM: E[rp] = 4% + 0. 96[14% - 4%] = 13. 6% * If A and B are on the SML => p is also on SML

Summary and Conclusions o o o The CAPM is a theory that provides a relation between expected return and an asset’s risk. It is based on investors being well-diversified and choosing non-dominated portfolios that consist of combinations of f (risk free security) and M. While the CAPM is useful for considering the risk/return tradeoff, and it is still used by many practitioners, it is but one of many theories relating return to risk (and other factors) so it should not be regarded as a universal truth.
 Capital market line
Capital market line Derivation of capm
Derivation of capm Capm excel
Capm excel Capm formula excel
Capm formula excel Capital allocation line formula
Capital allocation line formula Business vs financial risk
Business vs financial risk Credit risk market risk operational risk
Credit risk market risk operational risk Multi factor pricing model
Multi factor pricing model Ellipse software training
Ellipse software training Andrea frazzini
Andrea frazzini Fundamental theorem of asset pricing proof
Fundamental theorem of asset pricing proof Product line decisions
Product line decisions Target rate of return pricing
Target rate of return pricing Noa turnover
Noa turnover Working capital management decisions help to determine
Working capital management decisions help to determine Human capital intangible asset
Human capital intangible asset Jasa capital asset management
Jasa capital asset management Kospin jasa
Kospin jasa Risk and return
Risk and return Risk and return
Risk and return Risk and return
Risk and return Multifactor model of risk and return
Multifactor model of risk and return Financial management chapter 8 risk and return
Financial management chapter 8 risk and return Chapter 13 return risk and the security market line
Chapter 13 return risk and the security market line Introduction to risk and return
Introduction to risk and return Risk and return
Risk and return Chapter 8 risk and rates of return problem solutions
Chapter 8 risk and rates of return problem solutions Contoh risk and return
Contoh risk and return Difference between risk and return
Difference between risk and return Chapter 5 risk and return
Chapter 5 risk and return Difference between risk and return
Difference between risk and return Risk and return
Risk and return Konsep risk and return
Konsep risk and return Required rate of return formula
Required rate of return formula Capital employed formula
Capital employed formula Goodwill advantages and disadvantages
Goodwill advantages and disadvantages


























































