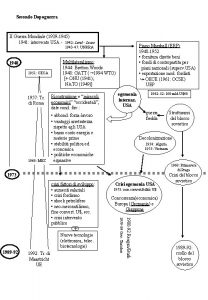
Ricerca Operativa Primi sviluppi seconda guerra mondiale Dopoguerra

Ricerca Operativa • • • Primi sviluppi : seconda guerra mondiale Dopoguerra: applicazioni civili Standardizzazione Sviluppo del calcolo automatico Campi applicativi: Industria Trasporti Finanze Etc. 1

Definizione secondo Ackoff-Sasieni: La Ricerca Operativa e’: 1. 2. 3. l’applicazione del metodo scientifico da parte di gruppi interdisciplinari a problemi che implicano il controllo di sistemi organizzati al fine di fornire soluzioni che meglio servano gli scopi dell’organizzazione nel suo insieme 2

Caratteristiche della Ricerca Operativa 1. La R. O. viene applicata alla risoluzione di problemi sul come condurre, organizzare e migliorare le operazioni e le attivita’ all’interno di una organizzazione 2. L’approccio utilizzato e’ quello del metodo scientifico: individuato il problema si costruisce il modello matematico che astrae l’essenza dal problema reale 3. La R. O. cerca di risolvere i conflitti fra le varie componenti del sistema visto nel suo insieme: gli obiettivi prefissati devono essere in accordo con tutta l’organizzazione 4. La R. O. non si limita ad individuare una delle possibili soluzioni del problema, ma individua, se possibile, quella ottimale, cioe’ quella che meglio risponde alle esigenze. 3

Esempio Gestione linea metropolitana • Variabili: Numero treni, Tempi di attesa • Funzione Obiettivo • Esigenze diverse Ente gestore Utenti • Vincoli 4

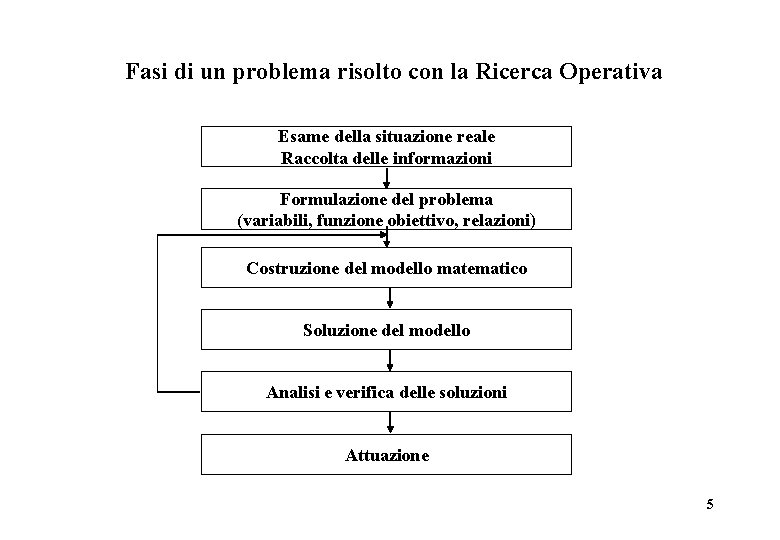
Fasi di un problema risolto con la Ricerca Operativa Esame della situazione reale Raccolta delle informazioni Formulazione del problema (variabili, funzione obiettivo, relazioni) Costruzione del modello matematico Soluzione del modello Analisi e verifica delle soluzioni Attuazione 5

Problemi economici Vincoli Ottimizzare • • • Costi Profitti Produzione Gestione Organizzazione • • Organizzativi Logistici Finanziari Produttivi Costi fissi Costi variabili lineari Costi variabili non lineari 6

Problemi economici in una sola variabile X = quantita’ di merce prodotta e/o venduta (x ≥ 0) C(X) = Costo totale Cu(X) = C(X) / X = Costo unitario R(X) = Ricavo della vendita G(X) = Guadagno o utile netto pu = prezzo unitario di vendita = Costante Funzione della domanda (ricavato da una stima statistica) 7

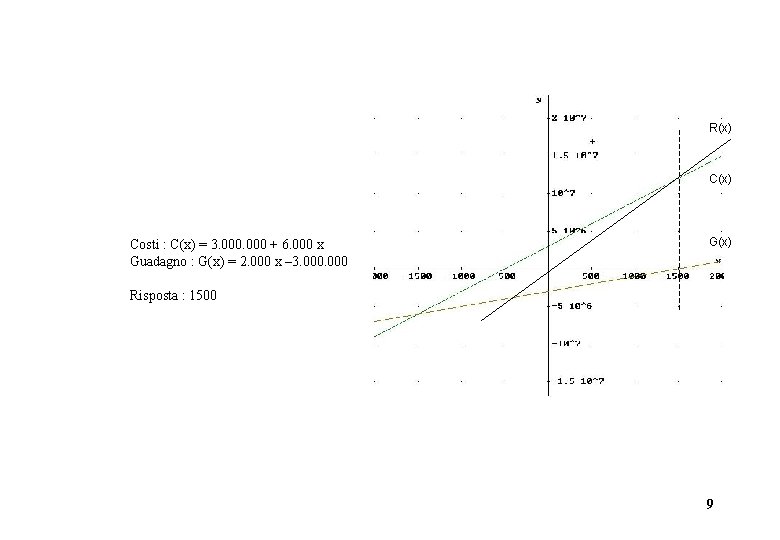
PROBLEMI ECONOMICI 1) Un’impresa produce un prodotto sostenendo una spesa fissa mensile di 3. 000 u. m. ed una spesa variabile di 6000 u. m. per ogni unità di prodotto. Il prezzo di vendita è di 8000 u. m. per unità. Determinare e disegnare le funzioni spesa e guadagno mensili in funzione della quantità x prodotta. Quale quantità minima è necessario produrre per non lavorare in perdita? u. m. =unità monetarie 8

R(x) Costi : C(x) = 3. 000 + 6. 000 x Guadagno : G(x) = 2. 000 x – 3. 000 Risposta : 1500 G(x) 9

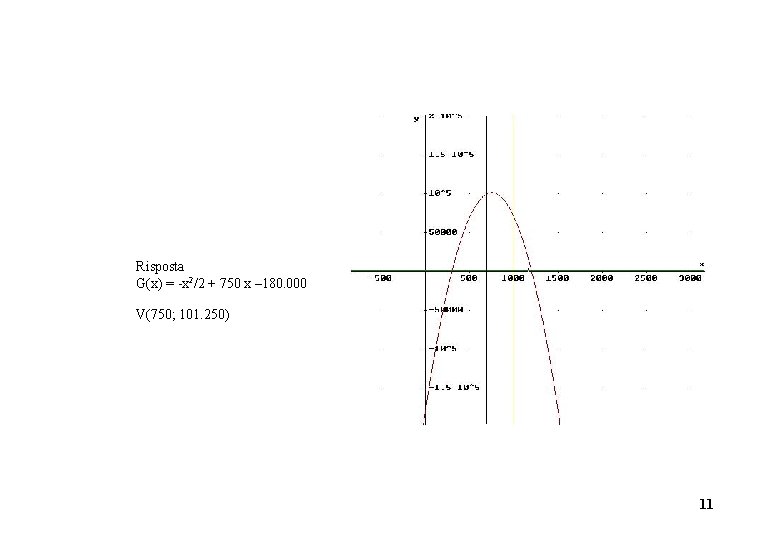
2) Un’impresa produce un prodotto sostenendo una spesa fissa mensile di 180. 000 u. m. , un costo di produzione unitario di 50 u. m. , una spesa unitaria di vendita pari alla metà del prodotto venduto. Il prezzo di vendita è di 800 u. m. per prodotto. La quantità massima che può essere prodotta è 1000 unità di prodotto. Determinare e disegnare la funzione guadagno mensile. (Esaminare anche con vincolo sulla produzione x 700) 10

Risposta G(x) = -x 2/2 + 750 x – 180. 000 V(750; 101. 250) 11

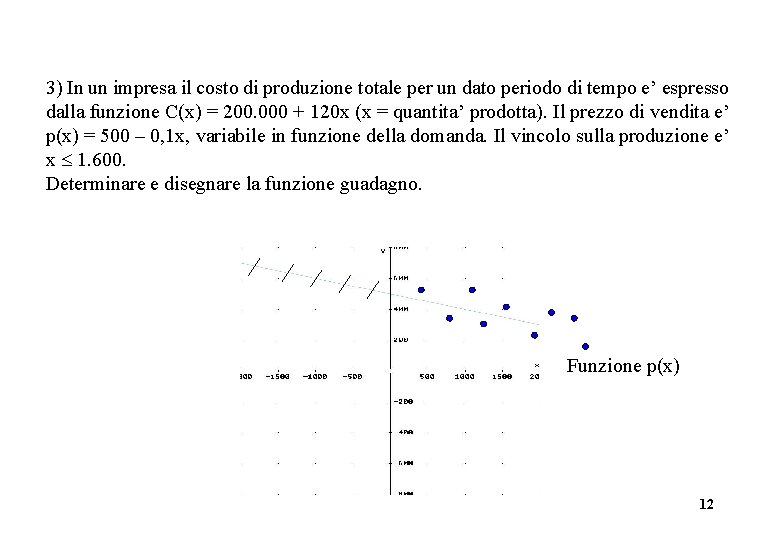
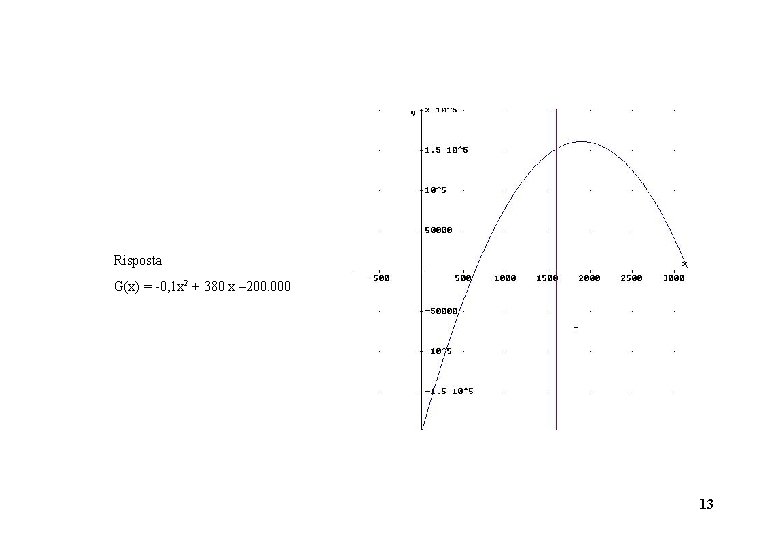
3) In un impresa il costo di produzione totale per un dato periodo di tempo e’ espresso dalla funzione C(x) = 200. 000 + 120 x (x = quantita’ prodotta). Il prezzo di vendita e’ p(x) = 500 – 0, 1 x, variabile in funzione della domanda. Il vincolo sulla produzione e’ x 1. 600. Determinare e disegnare la funzione guadagno. Funzione p(x) 12

Risposta G(x) = -0, 1 x 2 + 380 x – 200. 000 13

4) Una ditta ha una capacità produttiva mensile di kg. 1500 di una merce. Per la produzione sostiene una spesa fissa mensile di 500. 000 u. m. ed un costo di u 1000 per ogni kg prodotto. La domanda della merce ( ossia la quantità di merce richiesta dai consumatori ) è espressa in funzione del prezzo dalla relazione : x(p) = 2400 – 0, 4 p dove x è la quantità richiesta e p è il prezzo al kg. Calcolare la quantità che si deve produrre per ottenere il massimo utile, nell’ipotesi che tutta la quantità prodotta sia venduta. 14

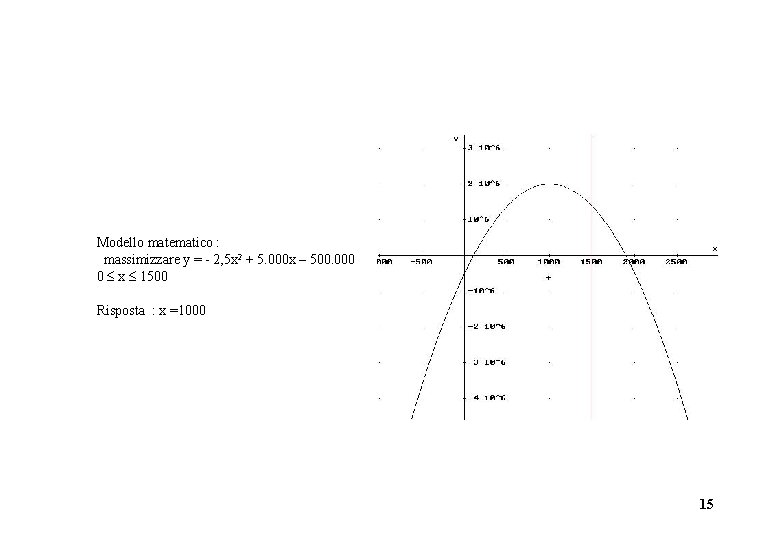
Modello matematico : massimizzare y = - 2, 5 x 2 + 5. 000 x – 500. 000 0 x 1500 Risposta : x =1000 15

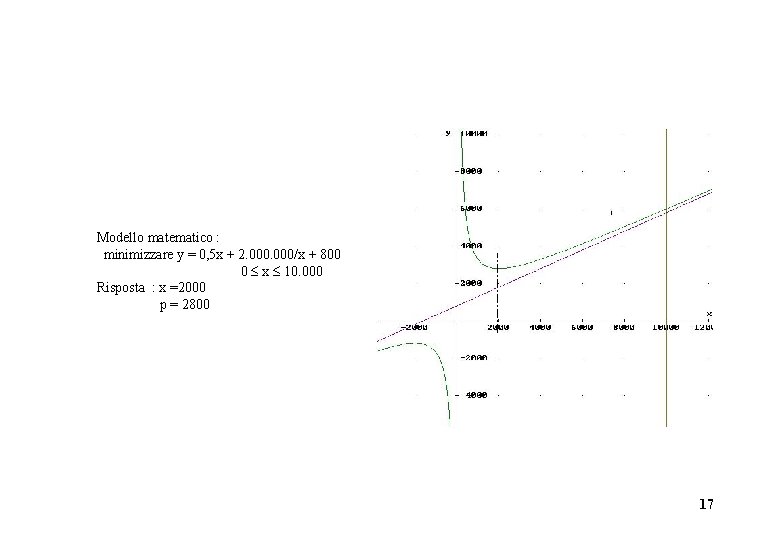
5) Per la produzione di un bene un’ impresa sostiene una spesa fissa di 2. 000 u. m. , un costo unitario di 800 u. m. per ogni unità prodotta e una spesa, stimata pari allo 0, 5 del quadrato della quantità prodotta, per la manutenzione degli impianti. La capacità produttiva massima mensile è di 10. 000 unità. Determinare per quale quantità il costo unitario di produzione è minimo. 16

Modello matematico : minimizzare y = 0, 5 x + 2. 000/x + 800 0 x 10. 000 Risposta : x =2000 p = 2800 17

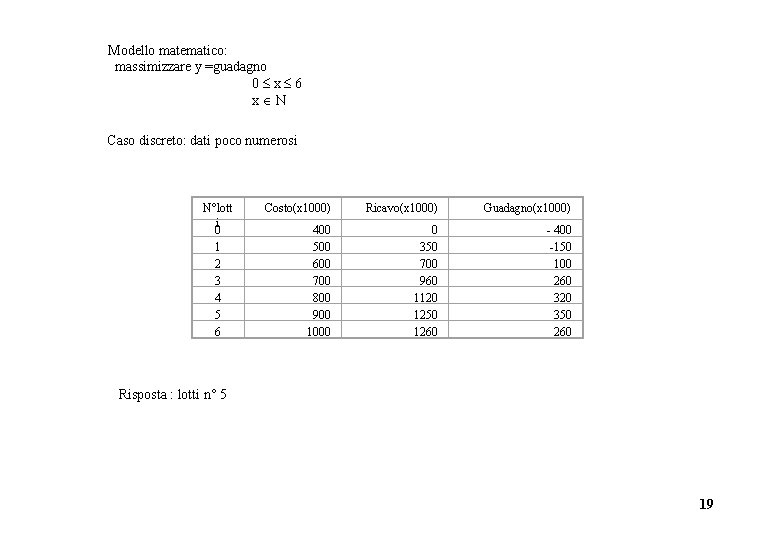
6) Un prodotto è fabbricato e venduto in lotti da 200 pezzi ciascuno. Per la lavorazione si sostiene una spesa fissa giornaliera di u. m. 400. 000 ed un costo di u. m. 500 al pezzo, ed il numero massimo di lotti prodotti in un giorno è di 6. Il prezzo di vendita è decrescente al crescere del numero di lotti venduti secondo la seguente tabella N. lotti Prezzo al lotto (x 1000) 1 350 2 350 3 320 4 280 5 250 6 210 Determinare quanti lotti si devono produrre giornalmente per realizzare il massimo utile. 18

Modello matematico: massimizzare y =guadagno 0 x 6 x N Caso discreto: dati poco numerosi N°lott i 0 1 2 3 4 5 6 Costo(x 1000) Ricavo(x 1000) Guadagno(x 1000) 400 500 600 700 800 900 1000 0 350 700 960 1120 1250 1260 - 400 -150 100 260 320 350 260 Risposta : lotti n° 5 19

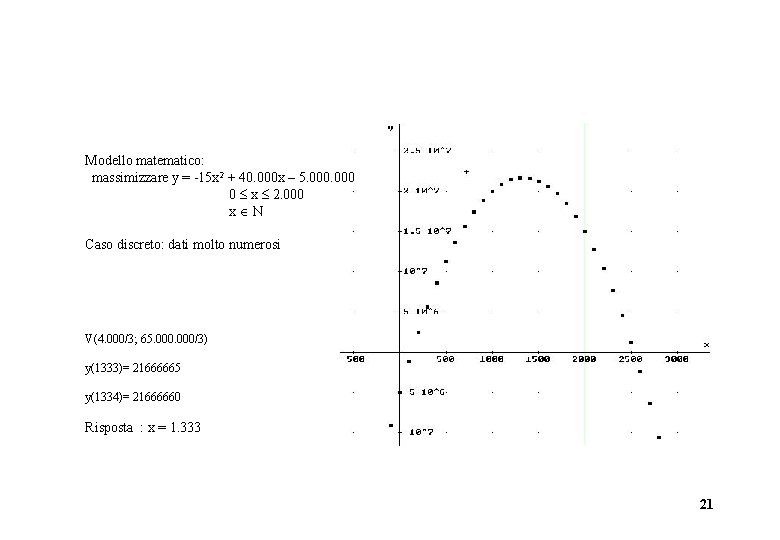
7) Una ditta produce beni in unità non divisibili (es. abiti) e deve decidere il numero di beni da produrre mensilmente per ottenere l’utile massimo. I dati tecnici sono i seguenti : costo unitario per materia prima e lavorazione u. m. 20. 000, spesa fissa mensile u. m. 5. 0000, prezzo di vendita p = 60. 00015 x (dove x è il numero dei beni). Calcolare quante unità del bene produrre per ottimizzare l’utile netto, sapendo che la massima capacità produttiva è 2. 000 unità al mese. 20

Modello matematico: massimizzare y = -15 x 2 + 40. 000 x – 5. 000 0 x 2. 000 x N Caso discreto: dati molto numerosi V(4. 000/3; 65. 000/3) y(1333)= 21666665 y(1334)= 21666660 Risposta : x = 1. 333 21

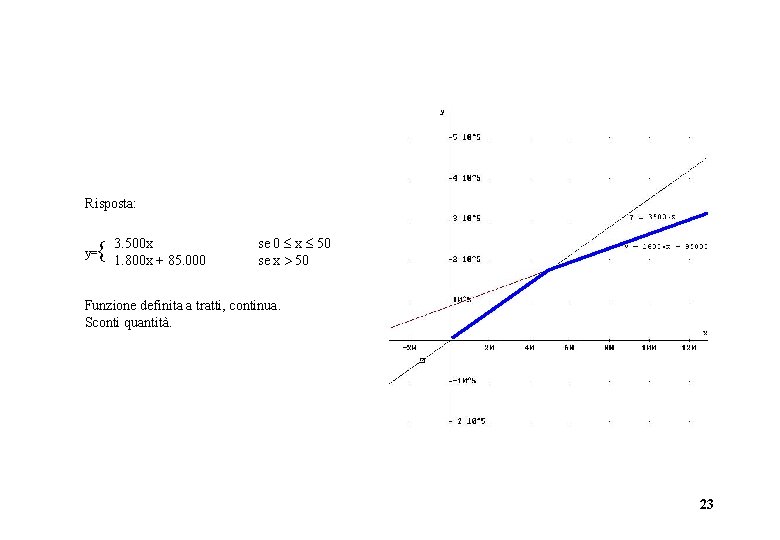
8) Una ditta per un servizio di trasporto pratica i seguenti prezzi: 3. 500 u. m. al quintale fino a 50 quintali e 1. 800 u. m. al quintale per ogni quintale eccedente i 50. Indicando con x il numero di quintali determinare l’espressione del costo totale in funzione di x. 22

Risposta: 3. 500 x 1. 800 x + 85. 000 y= se 0 x 50 se x 50 Funzione definita a tratti, continua. Sconti quantità. 23

9) Un commerciante, che ha una capacità di magazzino di 300 kg. , può acquistare una merce a 50. 000 u. m. al Kg; se la quantità acquistata supera 100 Kg. egli usufruisce di uno sconto del 20% sull’eccedenza. Tenendo conto del fatto che all’atto dell’acquisto egli deve sostenere un costo fisso di 1. 000 u. m. , e che il prezzo unitario di rivendita della merce e’ dato da p = 80. 000 – 100 x, determinare quale quantità deve essere acquistata e venduta per ottenere il massimo guadagno. 24

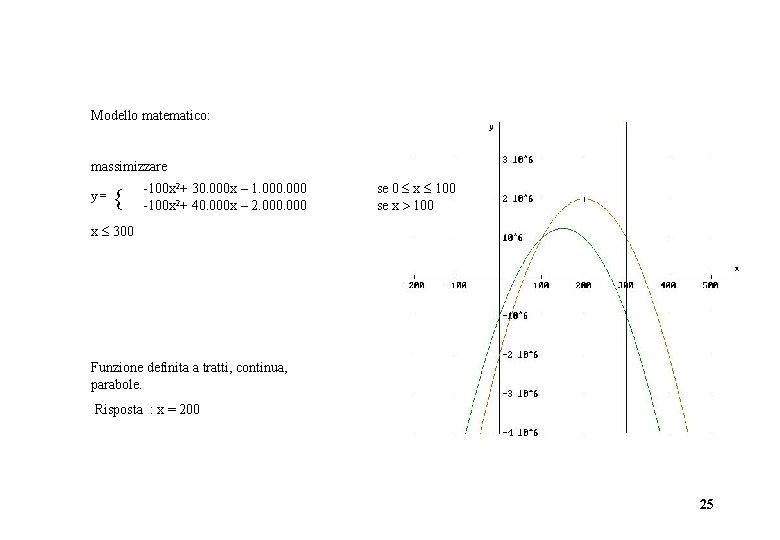
Modello matematico: massimizzare y = -100 x 2+ 30. 000 x – 1. 000 -100 x 2+ 40. 000 x – 2. 000 se 0 x 100 se x 100 x 300 Funzione definita a tratti, continua, parabole. Risposta : x = 200 25

10) Un impresa commerciale acquista della merce e la rivende ai dettaglianti. Il costo della merce e’ di 300 u. m al Kg. ; per acquisti di almeno 30 q. il prezzo e’ ridotto a 250 u. m. il Kg. La domanda e’ data dalla funzione x = 10. 000– 10 p. L’impresa sostiene settimanalmente una spesa fissa di 200. 000 u. m e puo’ acquistare al massimo 50 q di merce. Calcolare quanti Kg. di merce si devono acquistare per ottenere il massimo utile nell’ipotesi che tutta la quantita’ acquistata sia rivenduta. 26

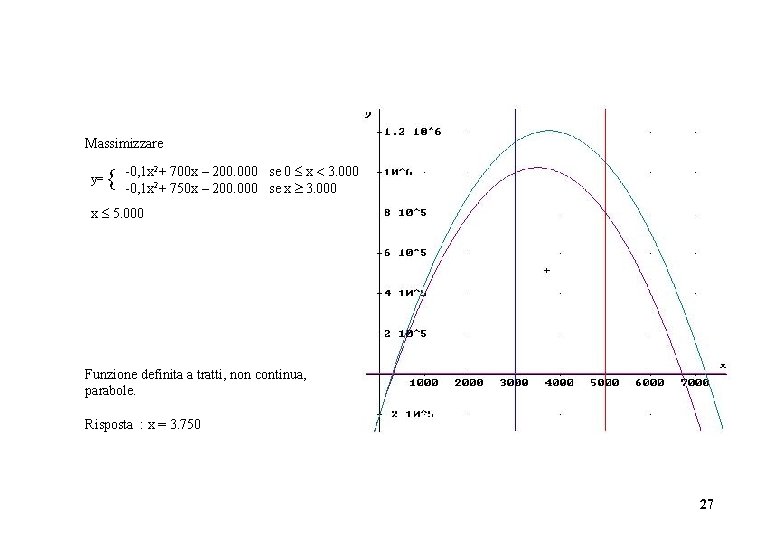
Massimizzare y= -0, 1 x 2+ 700 x – 200. 000 se 0 x 3. 000 -0, 1 x 2+ 750 x – 200. 000 se x 3. 000 x 5. 000 Funzione definita a tratti, non continua, parabole. Risposta : x = 3. 750 27

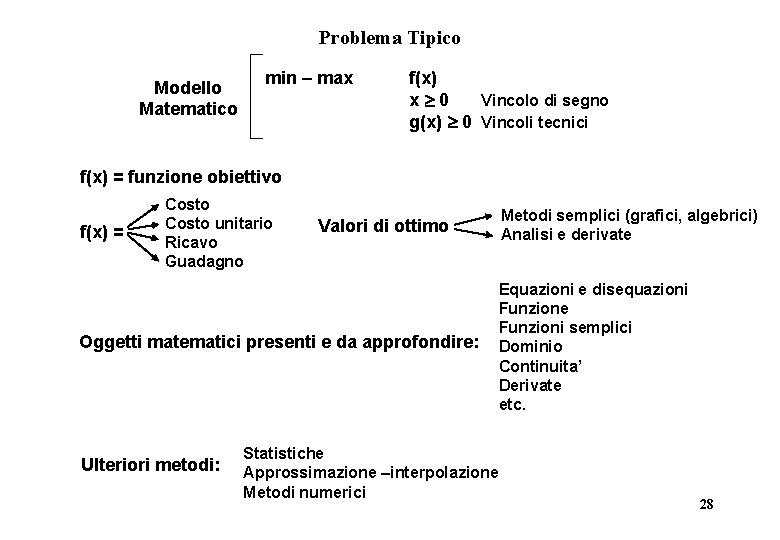
Problema Tipico Modello Matematico min – max f(x) x 0 Vincolo di segno g(x) 0 Vincoli tecnici f(x) = funzione obiettivo f(x) = Costo unitario Ricavo Guadagno Valori di ottimo Oggetti matematici presenti e da approfondire: Ulteriori metodi: Statistiche Approssimazione –interpolazione Metodi numerici Metodi semplici (grafici, algebrici) Analisi e derivate Equazioni e disequazioni Funzione Funzioni semplici Dominio Continuita’ Derivate etc. 28

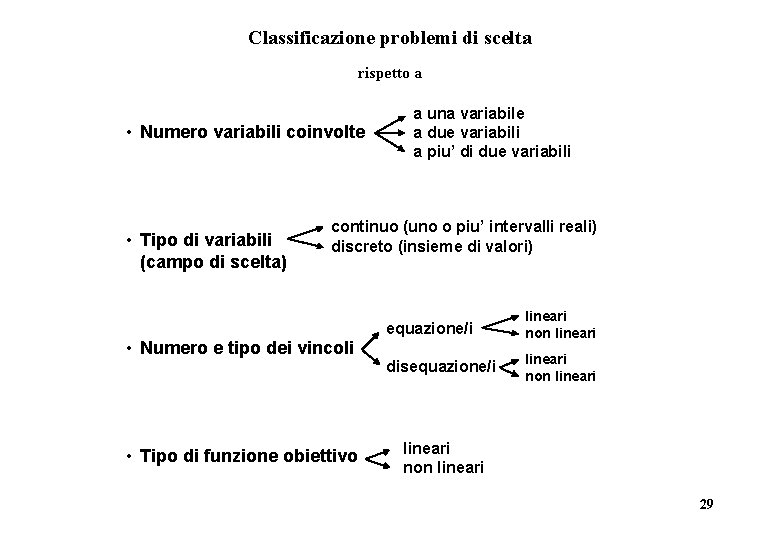
Classificazione problemi di scelta rispetto a • Numero variabili coinvolte • Tipo di variabili (campo di scelta) a una variabile a due variabili a piu’ di due variabili continuo (uno o piu’ intervalli reali) discreto (insieme di valori) • Numero e tipo dei vincoli • Tipo di funzione obiettivo equazione/i lineari non lineari disequazione/i lineari non lineari 29

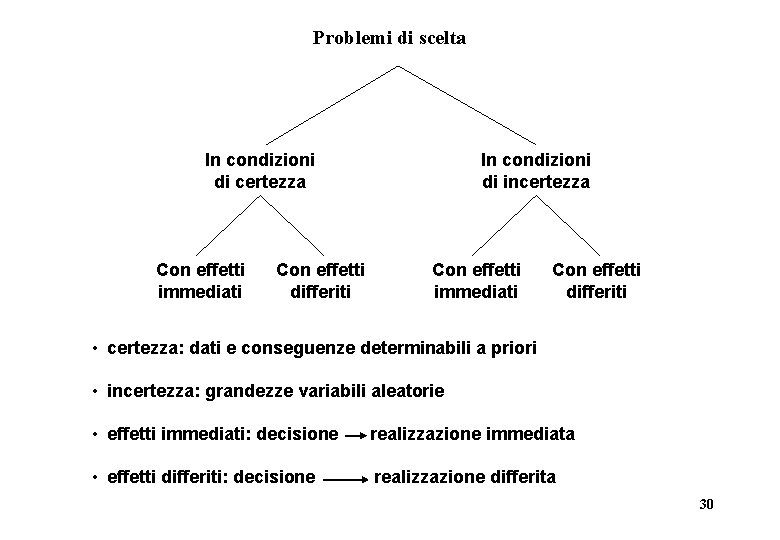
Problemi di scelta In condizioni di certezza Con effetti immediati Con effetti differiti In condizioni di incertezza Con effetti immediati Con effetti differiti • certezza: dati e conseguenze determinabili a priori • incertezza: grandezze variabili aleatorie • effetti immediati: decisione realizzazione immediata • effetti differiti: decisione realizzazione differita 30

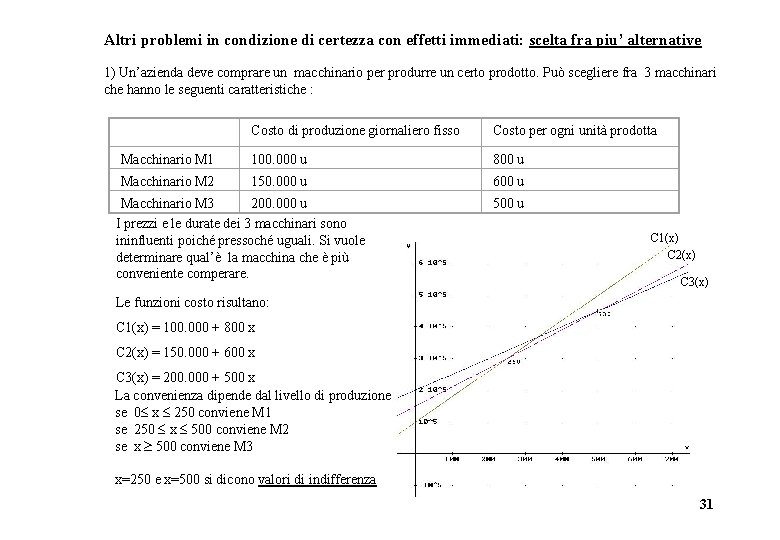
Altri problemi in condizione di certezza con effetti immediati: scelta fra piu’ alternative 1) Un’azienda deve comprare un macchinario per produrre un certo prodotto. Può scegliere fra 3 macchinari che hanno le seguenti caratteristiche : Costo di produzione giornaliero fisso Costo per ogni unità prodotta Macchinario M 1 100. 000 u 800 u Macchinario M 2 150. 000 u 600 u Macchinario M 3 200. 000 u I prezzi e le durate dei 3 macchinari sono ininfluenti poiché pressoché uguali. Si vuole determinare qual’è la macchina che è più conveniente comperare. 500 u C 1(x) C 2(x) C 3(x) Le funzioni costo risultano: C 1(x) = 100. 000 + 800 x C 2(x) = 150. 000 + 600 x C 3(x) = 200. 000 + 500 x La convenienza dipende dal livello di produzione : se 0 x 250 conviene M 1 se 250 x 500 conviene M 2 se x 500 conviene M 3 x=250 e x=500 si dicono valori di indifferenza 31

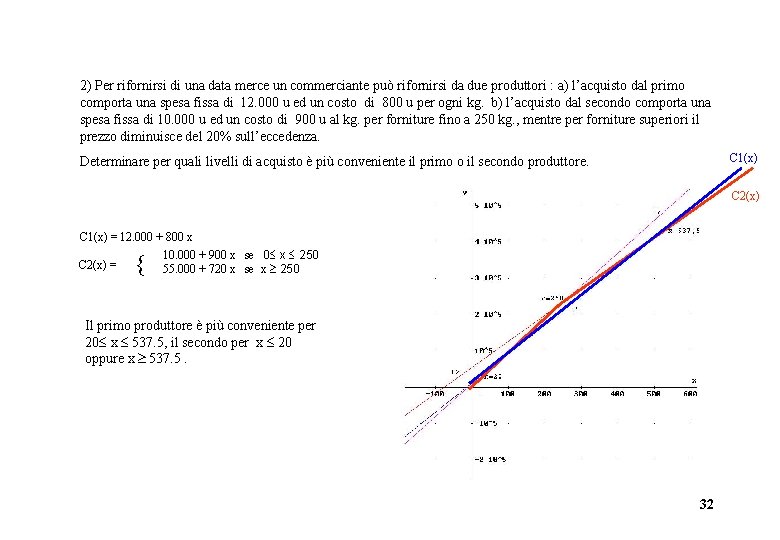
2) Per rifornirsi di una data merce un commerciante può rifornirsi da due produttori : a) l’acquisto dal primo comporta una spesa fissa di 12. 000 u ed un costo di 800 u per ogni kg. b) l’acquisto dal secondo comporta una spesa fissa di 10. 000 u ed un costo di 900 u al kg. per forniture fino a 250 kg. , mentre per forniture superiori il prezzo diminuisce del 20% sull’eccedenza. C 1(x) Determinare per quali livelli di acquisto è più conveniente il primo o il secondo produttore. C 2(x) C 1(x) = 12. 000 + 800 x 10. 000 + 900 x se 0 x 250 C 2(x) = 55. 000 + 720 x se x 250 Il primo produttore è più conveniente per 20 x 537. 5, il secondo per x 20 oppure x 537. 5. 32

Problemi di scelta in condizione di certezza con effetti differiti Esempio 1 Si vogliono investire 10. 000 di u. m. e si puo’ scegliere tra: a) ricevere tra 10 anni u. m. 25. 000 b) ricevere tra 8 anni u. m. 25. 000 La scelta b) non comporta alcun dubbio Esempio 2 Si vogliono investire 10. 000 u. m. e si puo’ scegliere tra: a) ricevere tra 10 anni u. m. 25. 000 b) ricevere tra 3 anni u. m. 8. 000 e fra 9 anni altri 9. 000 Problemi tipici: • Finanziari (acquisti o vendite di beni economici, etc. ) • Commerciali (gestione di attivita’ commerciali, apertura di agenzie, etc. ) • Industriali (acquisto, noleggio apparecchiature, etc. ) 33

Criteri utilizzati: • Criterio attualizzazione Confronto dei rendimenti economici attualizzati (r. e. a. ): valori attuali, all’inizio dell’attivita’, dei costi e ricavi futuri Difetto: criterio soggettivo (scelta del tasso di attualizzazione) • Criterio del tasso effettivo di impiego (o tasso interno di rendimento) Calcolo del tasso per cui il valore attuale dei costi e’ uguale al valore attuale dei ricavi, per ciascun caso Criterio oggettivo Difetto: scadenze comparabili La scelta dipende dall’obiettivo: investimento o costo 34

Esempio 2 Si vogliono investire 10. 000 di u. m. e si puo’ scegliere tra: a) ricevere tra 10 anni u. m. 25. 000 b) ricevere tra 3 anni u. m. 8. 000 e fra 9 anni altri 9. 000 Svolgimento Criterio attualizzazione Va = 25. 000 (1 + i)-10 V = 8. 000 (1 + i)-3 + 9. 000 (1 + i)-9 b i = 8% Va = 11. 579. 000 Vb = 10. 852. 000 Soluzione: e’ piu’ conveniente a) i = 12% Va = 8. 049. 000 Vb = 8. 939. 000 Soluzione: e’ piu’ conveniente b) Criterio tasso effettivo di impiego a) 10. 000 = 25. 000 (1 + i)-10 Soluzione: i = 9, 59% (metodi algebrici di calcolo) b) 10. 000 = 8. 000 (1 + i)-3 + 9. 000 (1 + i)-9 Soluzione: i = 9, 64% (metodi numerici di calcolo) 35

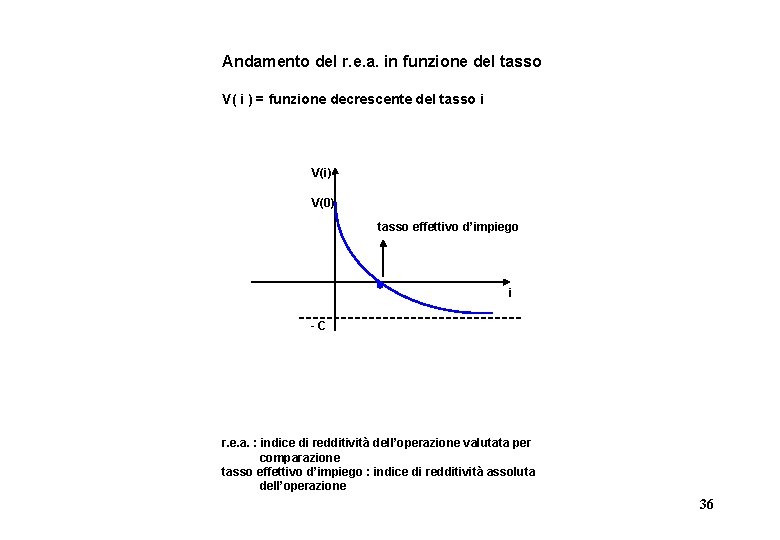
Andamento del r. e. a. in funzione del tasso V( i ) = funzione decrescente del tasso i V(i) V(0) tasso effettivo d’impiego i -C r. e. a. : indice di redditività dell’operazione valutata per comparazione tasso effettivo d’impiego : indice di redditività assoluta dell’operazione 36

Problemi di scelta in condizioni di incertezza con effetti immediati • • Le conseguenze dipendono da eventi aleatori Matrice dei risultati Eventi Esempio • …. . An Probabilita’ p 1 p 2 A 1 a 1, 1 a 2, 1 Alternative A 2 … … … E 1 E 2 …. . Eventi …. . Em am, 1 … … am, n pm E 1 E 2 E 3 E 4 A 1 5 5 Alternative A 2 4 5 6 7 A 3 2 4 7 10 Probabilita’ 0, 3 0, 25 Distribuzione di probabilita’ 37

• Criterio del valor medio 1. Per ogni alternativa M(AK) = i ai, k pi 2. Scelta dell’alternativa piu’ conveniente • Variabilita’ • Valutazione del rischio 1. Per ogni alternativa K = i [ ai, k - M(AK)]2 pi 2. Se valori medi uguali AK con K minore 3. Se valori medi diversi calcolo del livello di rischio LK = M(AK) / n (n = 1, 2, . . ) Se K LK (n fissato) si confrontano i valori medi e si sceglie il piu’ conveniente 38

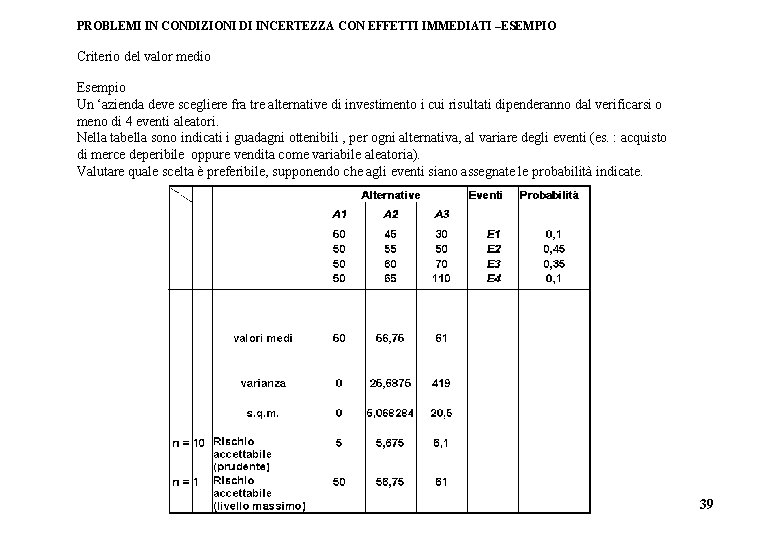
PROBLEMI IN CONDIZIONI DI INCERTEZZA CON EFFETTI IMMEDIATI –ESEMPIO Criterio del valor medio Esempio Un ‘azienda deve scegliere fra tre alternative di investimento i cui risultati dipenderanno dal verificarsi o meno di 4 eventi aleatori. Nella tabella sono indicati i guadagni ottenibili , per ogni alternativa, al variare degli eventi (es. : acquisto di merce deperibile oppure vendita come variabile aleatoria). Valutare quale scelta è preferibile, supponendo che agli eventi siano assegnate le probabilità indicate. 39

Problemi in condizioni di incertezza con effetti differiti • Eventi aleatori • Effetti differiti nel tempo • Applicazioni: Matematica attuariale 40

41

42