Relational Model Relational Algebra Relational Model u Terminology

Relational Model & Relational Algebra

Relational Model u Terminology of relational model. u How tables are used to represent data. u Connection between mathematical relations and relations in the relational model. u Properties of database relations. u How to identify candidate, primary, and foreign keys. u Meaning of entity integrity and referential integrity. 2

Relational Model Terminology u. A relation is a table with columns and rows. – Only applies to logical structure of the database, not the physical structure. u Attribute is a named column of a relation. u Domain is the set of allowable values for one or more attributes. 3

Relational Model Terminology u Tuple is a row of a relation. u Degree is the number of attributes in a relation. u Cardinality is the number of tuples in a relation. u Relational Database is a collection of normalized relations with distinct relation names. 4
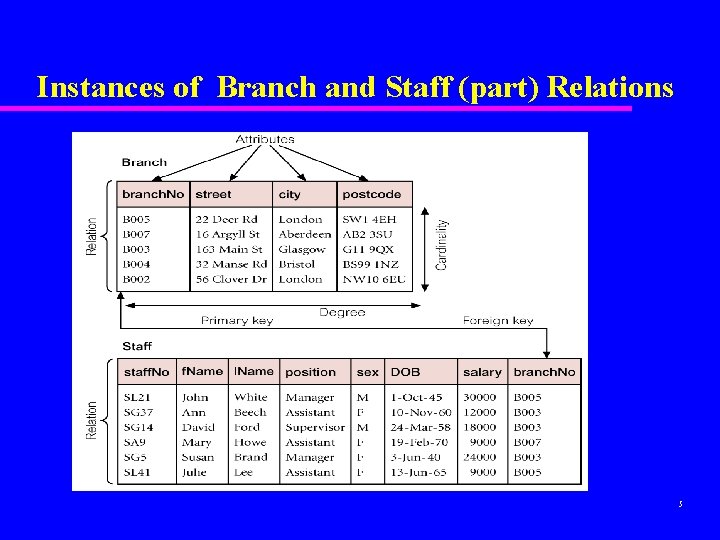
Instances of Branch and Staff (part) Relations 5
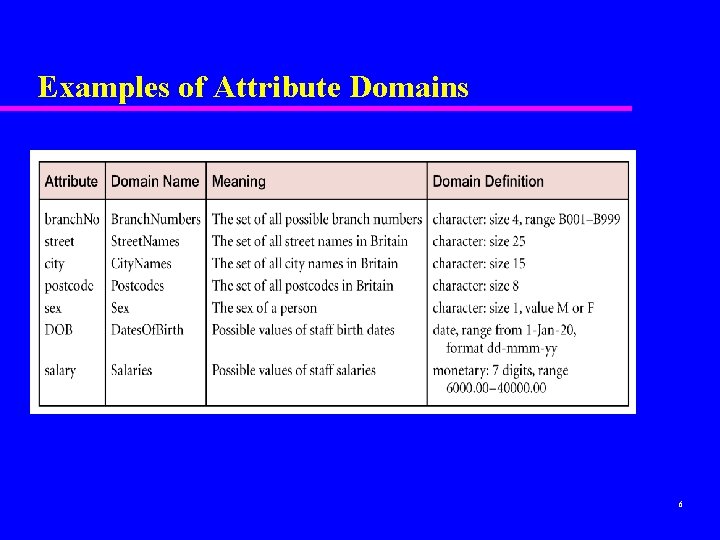
Examples of Attribute Domains 6

Alternative Terminology for Relational Model 7

Database Relations u Relation schema – Named relation defined by a set of attribute and domain name pairs. u Relational database schema – Set of relation schemas, each with a distinct name. 8

Properties of Relations u Relation name is distinct from all other relation names in relational schema. u Each cell of relation contains exactly one atomic (single) value. u Each attribute has a distinct name. u Values of an attribute are all from the same domain. 9

Properties of Relations u Each tuple is distinct; there are no duplicate tuples. u Order of attributes has no significance. u Order of tuples has no significance, theoretically. 10

Relational Keys u Superkey – An attribute, or a set of attributes, that uniquely identifies a tuple within a relation. u Candidate – – – Key Superkey (K) such that no proper subset is a superkey within the relation. In each tuple of R, values of K uniquely identify that tuple (uniqueness). No proper subset of K has the uniqueness property (irreducibility). 11

Relational Keys u Primary – Key Candidate key selected to identify tuples uniquely within relation. u Alternate – Keys Candidate keys that are not selected to be primary key. u Foreign Key – Attribute, or set of attributes, within one relation that matches candidate key of some (possibly same) relation. 12

Relational Integrity u Null – – – Represents value for an attribute that is currently unknown or not applicable for tuple. Deals with incomplete or exceptional data. Represents the absence of a value and is not the same as zero or spaces, which are values. 13

Relational Integrity u Entity Integrity – In a base relation, no attribute of a primary key can be null. u Referential Integrity – If foreign key exists in a relation, either foreign key value must match a candidate key value of some tuple in its home relation or foreign key value must be wholly null. u Enterprise Constraints – Additional rules specified by users or database administrators. 14

Relational Algebra u Meaning u How of the term relational completeness. to form queries in relational algebra. 15

Introduction u Relational algebra is a formal language associated with the relational model. u Informally, relational algebra is a (high-level) procedural language 16

Relational Algebra u Five basic operations in relational algebra: Selection, Projection, Cartesian product, Union, and Set Difference. u These perform most of the data retrieval operations needed. u Also have Join, Intersection which can be expressed in terms of 5 basic operations. 17

Relational Algebra Operations 18
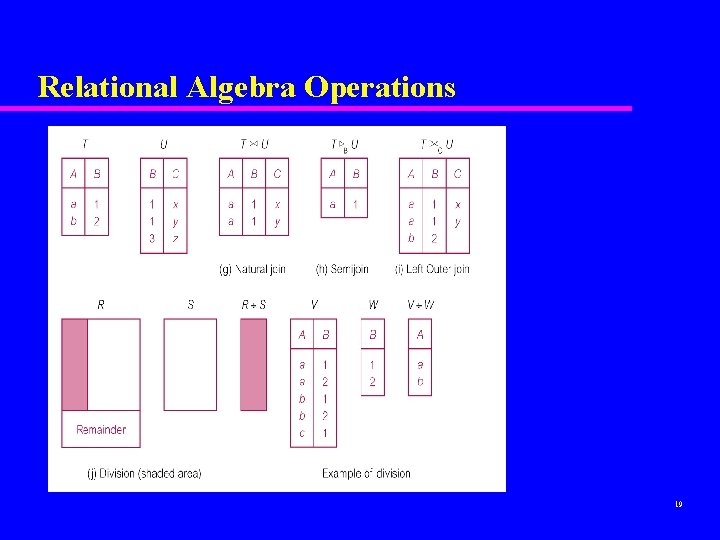
Relational Algebra Operations 19

Selection (or Restriction) u predicate (R) – Works on a single relation R and defines a relation that contains only those tuples (rows) of R that satisfy the specified condition (predicate). 20
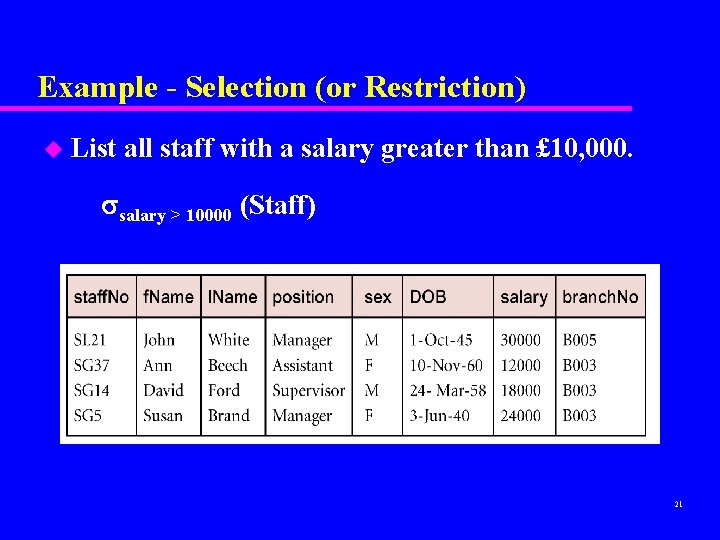
Example - Selection (or Restriction) u List all staff with a salary greater than £ 10, 000. salary > 10000 (Staff) 21

Projection u col 1, . . . , coln(R) – Works on a single relation R and defines a relation that contains a vertical subset of R, extracting the values of specified attributes and eliminating duplicates. 22

Example - Projection u Produce a list of salaries for all staff, showing only staff. No, f. Name, l. Name, and salary details. staff. No, f. Name, l. Name, salary(Staff) 23

Union S – Union of two relations R and S defines a relation that contains all the tuples of R, or S, or both R and S, duplicate tuples being eliminated. – R and S must be union-compatible. u. R u If R and S have I and J tuples, respectively, union is obtained by concatenating them into one relation with a maximum of (I + J) tuples. 24

Example - Union u List all cities where there is either a branch office or a property for rent. city(Branch) city(Property. For. Rent) 25

Set Difference u. R –S – Defines a relation consisting of the tuples that are in relation R, but not in S. – R and S must be union-compatible. 26

Example - Set Difference u List all cities where there is a branch office but no properties for rent. city(Branch) – city(Property. For. Rent) 27

Intersection S – Defines a relation consisting of the set of all tuples that are in both R and S. – R and S must be union-compatible. u. R u Expressed using basic operations: R S = R – (R – S) 28

Example - Intersection u List all cities where there is both a branch office and at least one property for rent. city(Branch) city(Property. For. Rent) 29

Cartesian product u. R XS – Defines a relation that is the concatenation of every tuple of relation R with every tuple of relation S. 30

Example - Cartesian product u List the names and comments of all clients who have viewed a property for rent. ( client. No, f. Name, l. Name(Client)) X ( client. No, property. No, comment (Viewing)) 31

Example - Cartesian product and Selection u Use selection operation to extract those tuples where Client. client. No = Viewing. client. No((Õclient. No, f. Name, l. Name(Client)) (Õclient. No, property. No, comment(Viewing))) Cartesian product and Selection can be reduced to a single operation called a Join. u 32

Join Operations u Join is a derivative of Cartesian product. u Equivalent to performing a Selection, using join predicate as selection formula, over Cartesian product of the two operand relations. u One of the most difficult operations to implement efficiently in an RDBMS and one reason why RDBMSs have intrinsic performance problems. 33

Join Operations u Various forms of join operation – Theta join – Equijoin (a particular type of Theta join) – Natural join – Outer join – Semijoin 34
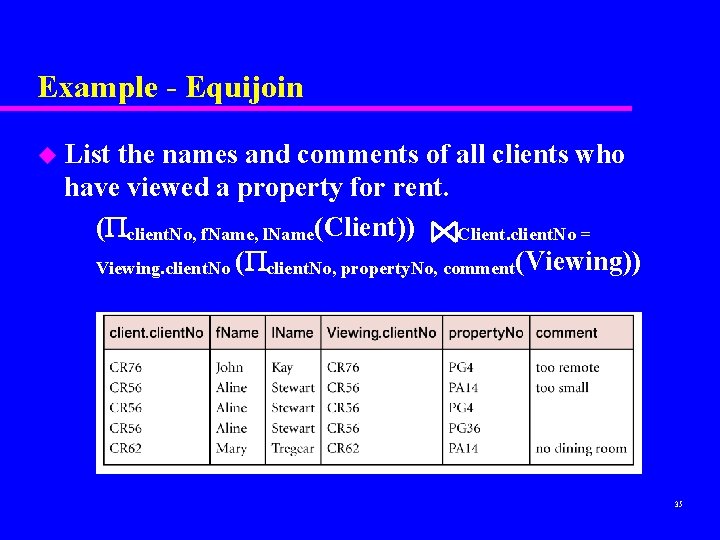
Example - Equijoin u List the names and comments of all clients who have viewed a property for rent. ( client. No, f. Name, l. Name(Client)) Client. client. No = Viewing. client. No ( client. No, property. No, comment(Viewing)) 35

Natural join u. R S – An Equijoin of the two relations R and S over all common attributes x. One occurrence of each common attribute is eliminated from the result. 36

Example - Natural join u List the names and comments of all clients who have viewed a property for rent. ( client. No, f. Name, l. Name(Client)) ( client. No, property. No, comment(Viewing)) 37
- Slides: 37