Lecture 07 Relational Algebra 1 Outline Relational Algebra

Lecture 07: Relational Algebra 1

Outline • Relational Algebra (Section 6. 1) 2
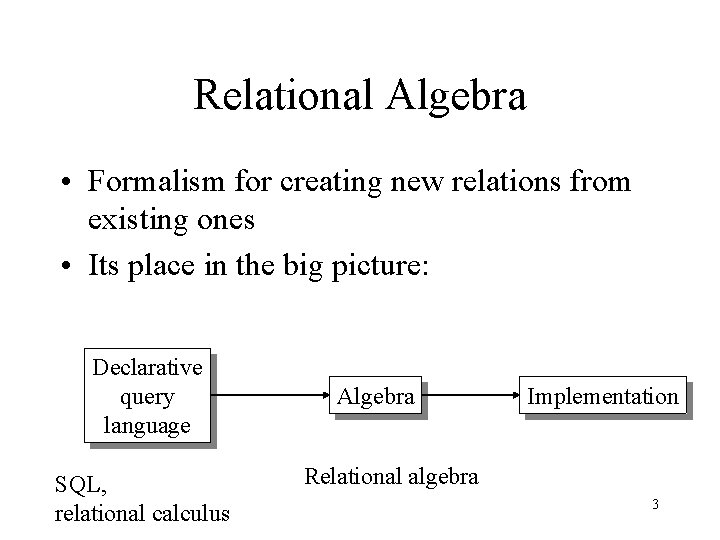
Relational Algebra • Formalism for creating new relations from existing ones • Its place in the big picture: Declarative query language SQL, relational calculus Algebra Implementation Relational algebra 3

Relational Algebra • Five operators: – – – Union: Difference: Selection: s Projection: P Cartesian Product: • Derived or auxiliary operators: – Intersection, complement – Joins (natural, equi-join, theta join, semi-join) – Renaming: r 4

1. Union and 2. Difference • R 1 R 2 Example: – Active. Employees Retired. Employees • R 1 – R 2 Example: – All. Employees − Retired. Employees 5

What about Intersection ? • It is a derived operator R 1 R 2 = R 1 – (R 1 – R 2) • Also expressed as a join (will see later) Example – Unionized. Employees Retired. Employees 6

3. Selection • Returns all tuples which satisfy a condition • Notation: sc(R) • Examples – s. Salary > 40000 (Employee) – sname = “Smith” (Employee) • The condition c can be =, <, , >, , <> [in SQL: SELECT * FROM Employee WHERE Salary > 40000] 7
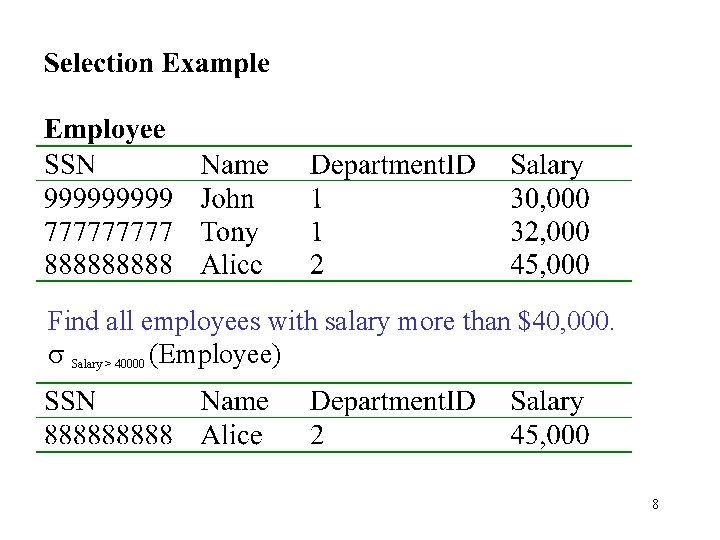
Find all employees with salary more than $40, 000. s Salary > 40000 (Employee) 8

4. Projection • Eliminates columns, then removes duplicates • Notation: P A 1, …, An (R) • Example: project to social-security number and names: – P SSN, Name (Employee) – Output schema: Answer(SSN, Name) [In SQL: SELECT DISTINCT SSN, Name FROM Employee] 9
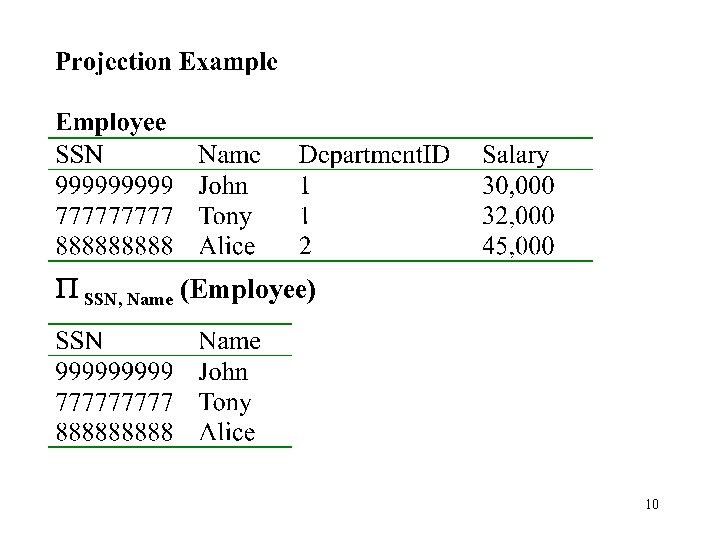
P SSN, Name (Employee) 10

5. Cartesian Product • Combine each tuple in R 1 with each tuple in R 2 • Notation: R 1 R 2 • Example: – Employee Dependents • Very rare in practice; mainly used to express joins [In SQL: SELECT * FROM R 1, R 2] 11

12

Relational Algebra • Five operators: – – – Union: Difference: Selection: s Projection: P Cartesian Product: • Derived or auxiliary operators: – Intersection, complement – Joins (natural, equi-join, theta join, semi-join) – Renaming: r 13

Renaming • • Changes the schema, not the instance Schema: R(A 1, …, An ) Notation: r B 1, …, Bn (R) Example: – r. Last. Name, Soc. No (Employee) – Output schema: Answer(Last. Name, Soc. No) [in SQL: SELECT Name AS Last. Name, SSN AS Soc. No 14 FROM Employee]

Renaming Example Employee Name John Tony r. Last. Name, Soc. No Last. Name John Tony SSN 99999 77777 (Employee) Soc. No 99999 77777 15

Natural Join • Notation: R 1 ⋈ R 2 • Meaning: R 1 ⋈ R 2 = PA(s. C(R 1 R 2)) • Where: – The selection s. C checks equality of all common attributes – The projection eliminates the duplicate common attributes [in SQL: R 2 SELECT DISTINCT R 1. A, R 1. B, R 2. C FROM R 1, WHERE R 1. B = R 2. B Schema: R 1(A, B), R 2(B, C)] 16

Natural Join Example Employee Name John Tony SSN 99999 77777 Dependents SSN 99999 77777 Dname Emily Joe Employee Dependents = PName, SSN, Dname(s SSN=SSN 2(Employee x r. SSN 2, Dname(Dependents)) Name John Tony SSN 99999 77777 Dname Emily Joe 17

Natural Join • R= • R ⋈ S= A B X S= B C Y Z U X Z V W Y Z Z V A B C X Z U X Z V Y Z U Y Z V W 18

Natural Join • Given the schemas R(A, B, C, D), S(A, C, E), what is the schema of R ⋈ S ? • Given R(A, B, C), S(D, E), what is R ⋈ S ? • Given R(A, B), S(A, B), what is R ⋈ S ? 19

Theta Join • A join that involves a predicate • R 1 ⋈ q R 2 = s q (R 1 R 2) • Here q can be any condition 20

Eq-join • A theta join where q is an equality R 1 ⋈A=B R 2 = s A=B (R 1 R 2) • Example: – Employee ⋈SSN=SSN Dependents • Most useful join in practice (difference to natural join? ) 21

Semijoin • R ⋉ S = P A 1, …, An (R ⋈ S) • Where A 1, …, An are the attributes in R • Example: – Employee ⋉ Dependents 22
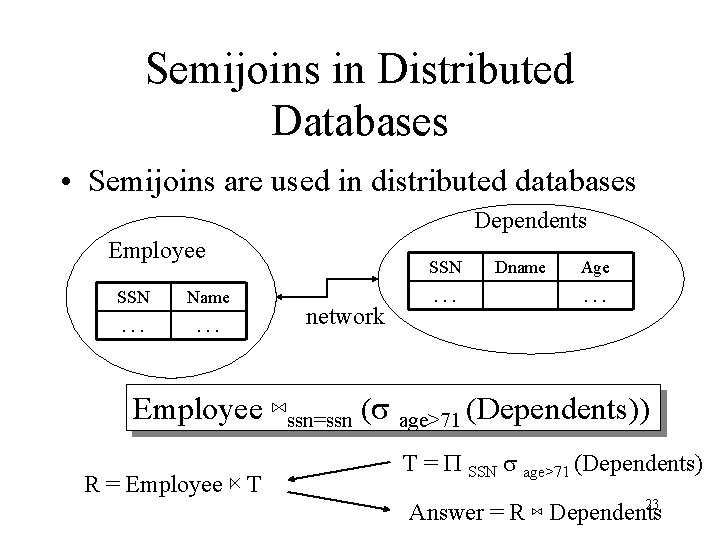
Semijoins in Distributed Databases • Semijoins are used in distributed databases Dependents Employee SSN Name . . . SSN network . . . Dname Age. . . Employee ⋈ssn=ssn (s age>71 (Dependents)) R = Employee ⋉ T T = P SSN s age>71 (Dependents) 23 Answer = R ⋈ Dependents
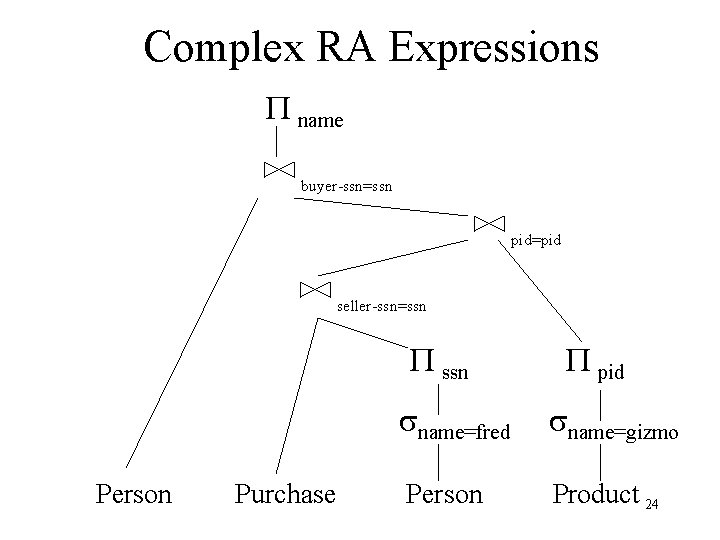
Complex RA Expressions P name buyer-ssn=ssn pid=pid seller-ssn=ssn Person Purchase P pid sname=fred sname=gizmo Person Product 24
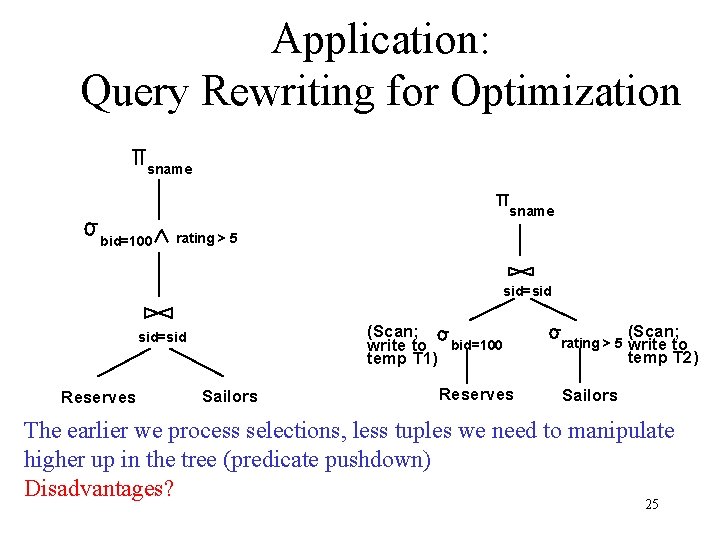
Application: Query Rewriting for Optimization sname bid=100 rating > 5 sid=sid (Scan; write to bid=100 temp T 1) sid=sid Reserves Sailors Reserves rating > 5 (Scan; write to temp T 2) Sailors The earlier we process selections, less tuples we need to manipulate higher up in the tree (predicate pushdown) Disadvantages? 25

Algebraic Laws (Examples) • Commutative and Associative Laws – R ∩ S = S ∩ R, R ∩ (S ∩ T) = (R ∩ S) ∩ T – R S = S R, R (S T) = (R S) T • Laws involving selection – s C AND C’(R) = s C(s C’(R)) = s C(R) ∩ s C’(R) – s C (R S) = s C (R) S • When C involves only attributes of R • Laws involving projections – PM(PN(R)) = PM, N(R) 26

Operations on Bags A bag = a set with repeated elements All operations need to be defined carefully on bags • {a, b, b, c} {a, b, b, b, e, f, f}={a, a, b, b, b, c, e, f, f} • {a, b, b, b, c, c} – {b, c, c, c, d} = {a, b, b, d} • s. C(R): preserve the number of occurrences • PA(R): no duplicate elimination • Cartesian product, join: no duplicate elimination Important ! Relational Engines work on bags, not sets ! 27

Finally: RA has Limitations ! • Cannot compute “transitive closure” Name 1 Name 2 Relationship Fred Mary Father Mary Joe Cousin Mary Bill Spouse Nancy Lou Sister • Find all direct and indirect relatives of Fred • Cannot express in RA !!! Need to write C program 28

Formulating queries in RA • Consider a database for student enrollment for courses, and books used in the courses – – – STUDENT (SSN, Name, Major, Bdate) COURSE (Course#, Cname, Dept) ENROLL (SSN, Course#, Quarter, Grade) BOOK_ADOPTION (Course#, Quarter, Book_ISBN) TEXT (Book_ISBN, Book_Title, Publisher, Author) 29

Formulating queries in RA • Specify the following queries in relational algebra – List the number of courses (Course#) taken by all students named ‘John Smith’ in Winter 1999 (i. e. , Quarter = W 99) – List any department which has all its adopted books published by ‘BC Publishing’ 30

Formulating Queries in RA § PCourse# (s Quarter=W 99 ((s Name= ‘John Smith’ (STUDENT) ⋈ ENROLL)) § Other. Dept = PDept ((s Publisher <> ‘PS Publishers’ (BOOK_ADOPTION ⋈ TEXT)) ⋈ COURSE) All. Dept = PDept (BOOK_ADOPTION ⋈ COURSE) WHY? Answer = All. Dept - Other. Dept § And how will you express it in SQL? 31
- Slides: 31



















































