Relational Algebra Relational Algebra Relational algebra was defined

Relational Algebra

Relational Algebra • Relational algebra was defined by Codd in 1971 as the basis for relational languages. • Theoretical basis for database functions

Relational Algebra • Forms the basis on which SQL was built – SQL is the “programming language” we use to interact with relational databases • Implementation of relational algebra in SQL might not match theory exactly—there are multiple forms of SQL • SQL is not a single uniform language – Most versions of SQL are more expressive and include such features as calculated fields, summary/aggregates, and ordering

Relational Algebra • Operations work on one or more table – to define another table without changing the original – Because both the input and output are tables, the output from one operation can be used as input in another operation – This allows “nesting” of operations—like when you use parentheses in “regular” algebra

Traditional Set Operators • Unary Operations work on 1 table – Selection – Projection • Binary Operations work on pairs of tables – Cartesian Product (Multiplication) – Union – Difference • Also: Join, Intersection, Division – Can be expressed in terms of the other 5
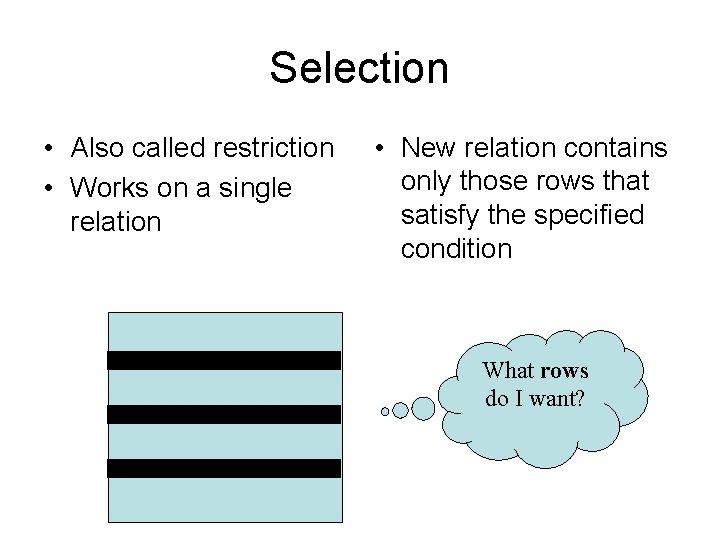
Selection • Also called restriction • Works on a single relation • New relation contains only those rows that satisfy the specified condition What rows do I want?

Selection • Selection retrieves specific rows according to a specified condition • Condition … where X theta Y – Theta means any sort of comparison • =, <, >, <>, =< , >= – Combine conditions with logical operators • ^ And • ۷ Or • ~ Not
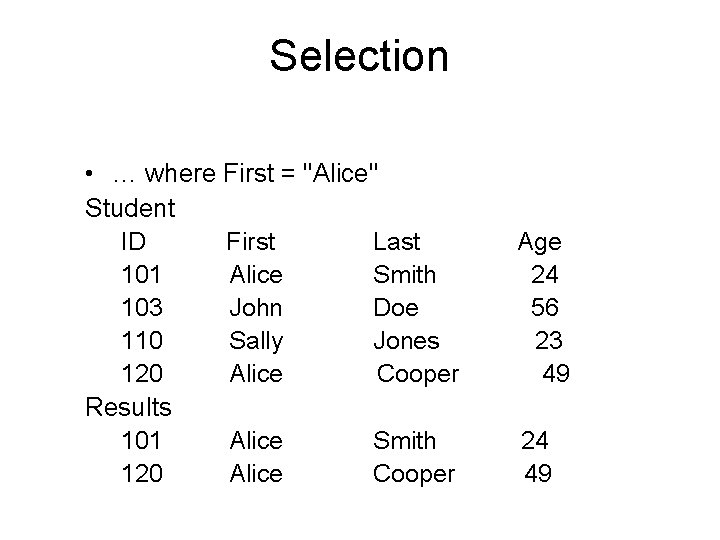
Selection • … where First = "Alice" Student ID 101 103 110 120 Results 101 120 First Alice John Sally Alice Last Smith Doe Jones Cooper Age 24 56 23 49 Alice Smith Cooper 24 49

Theta • Theta is part of the “where” clause in SQL • Must make sense for domain • … where First. Name > 50 Doesn’t make sense where age > 50

Projection • Works on a single relation • New relation is a vertical subset—that is, it contains only those attributes specified. • Duplicate rows are eliminated

Projection • Attributes return in the specified order • All unique rows in table A for attributes X, Y, & Z – Unique in this case means unique sets (X, Y, Z) – Although theory says unique, in SQL you must specify distinct “select DISTINCT X, Y, Z…”

Projection Example Students (SSN, Last, First, Age) ID First Last Age 101 Alice Smith 24 103 John Doe 56 110 Sally Jones 23 120 Alice Cooper 49 121 Sarah Doe 56 141 Anna Doe 44 Project the Students relation over the attributes (Last, Age)

Projection Example Results Smith Doe Jones Cooper 24 56 44 23 49 Why are there two “Doe” results? Why not three?

Set Operations • Selection and Projection ONLY work on a single relation (table). • If we want to select and/or project from multiple tables, we first have to combine the tables to form a single “virtual” table.

Joining tables that have similar attributes (Union, intersection, difference)

Union Operation • Tables A and B have similar attributes • We want rows from both tables

Union Operation • Combines tables “vertically” • Duplicates are eliminated • Relations must be “union-compatible” – same number of attributes – same domain for each attribute

Union Operation • Each attribute in table B must come from the same domain as the counterpart in table A • Don’t combine the following: – SSN First Last – SSN Street City Not the same attributes, even if they are the same data type! • Don’t combine the following: – SSN First Last Street

Union Operation Student … Student. ID Employee … Empl. ID Get the University ID and name for all students and employees Use Project to get the ID column and name from each table Use Union to join the results into a single result

Set Difference • All rows appearing in first, but not second table • Tables must be “union-compatible” – Like union, this is a “vertical” comparison! • Has direction –A-B B–A
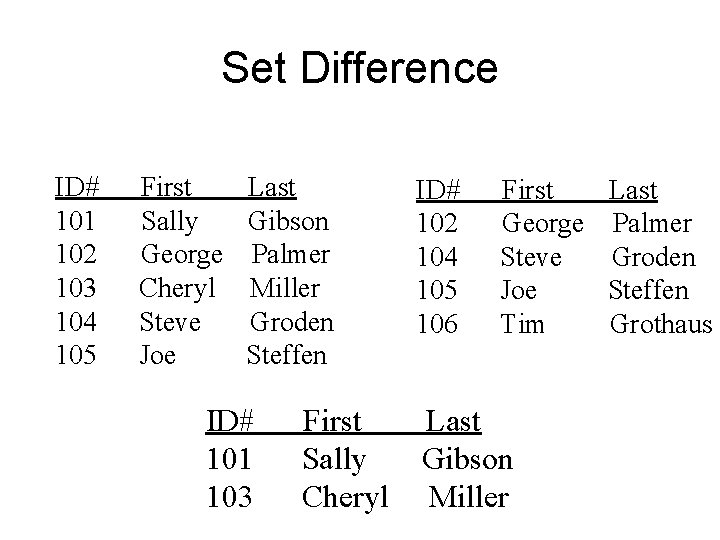
Set Difference ID# 101 102 103 104 105 First Sally George Cheryl Steve Joe Last Gibson Palmer Miller Groden Steffen ID# 101 103 First Sally Cheryl ID# 102 104 105 106 First George Steve Joe Tim Last Gibson Miller Last Palmer Groden Steffen Grothaus
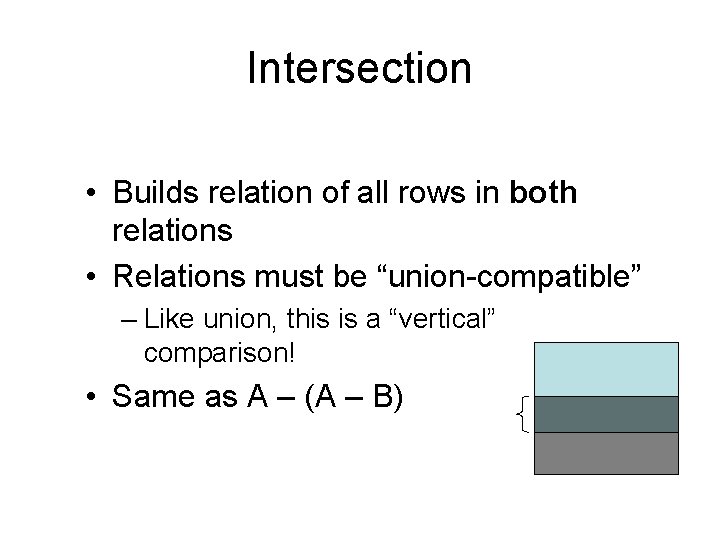
Intersection • Builds relation of all rows in both relations • Relations must be “union-compatible” – Like union, this is a “vertical” comparison! • Same as A – (A – B)

In SQL • You may use union • Seldom if ever see difference, intersection

Joining tables that have different attributes (Cartesian Product) Select and Project can only work on a single table. So we must merge the two tables into a single, “virtual” table before we can use Select and Project
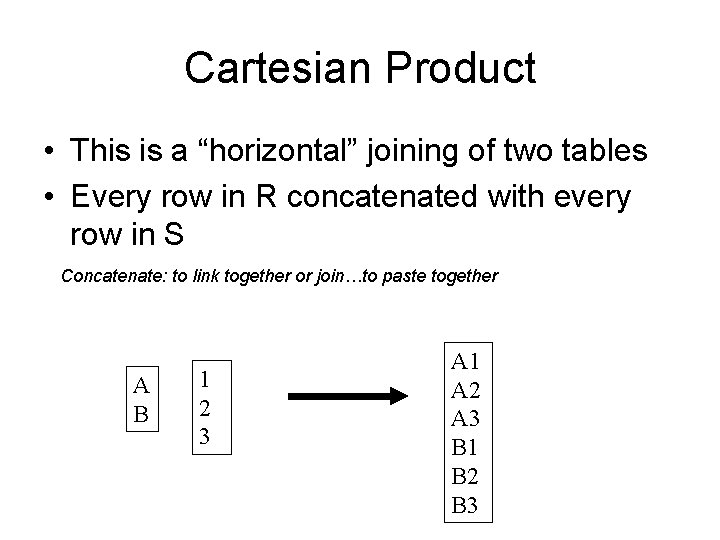
Cartesian Product • This is a “horizontal” joining of two tables • Every row in R concatenated with every row in S Concatenate: to link together or join…to paste together A B 1 2 3 A 1 A 2 A 3 B 1 B 2 B 3

Cartesian Product (Multiplication) • ALL POSSIBLE combinations of rows from two relations – Does not require same structure • If the two tables both have attributes with the same name, prefix the attribute name with the table name – Demog. pt_id – Vitals. pt_id

Cartesian Product • If relation A has I tuples and N attributes • and relation B has J tuples and M attributes… • A x B gives a relation with (I x J) tuples and (N + M) attributes • Employee (UNID, Last. Name, First. Name) 100 rows, 3 attributes • Student (UNID, Student. Type) 50 rows, 2 attributes • Person x Student has 5000 rows and 5 attributes

Cartesian product in SQL • It is what happens first when you query multiple tables • Not directly useful as is. We usually want only those rows where PK in one table is the same as FK in the other table. Other rows are meaningless. In previous example we really only want those records in both employee and student • If you get a Cartesian product as the output of an SQL statement, you need to re-look at your query

Rename (Alias) • Optional name, what you will call something temporarily employee. UNID as empl. ID student. UNID as student. ID • Can rename (alias) the input, the output relation (virtual table), and/or attributes If you alias employee (table) as e, you can ask for e. UNID instead of employee. UNID

JOINS • Typically only want the combinations within the Cartesian product that satisfy certain conditions. • We call this a JOIN • Cartesian product is then restricted to specific rows Where employee. UNID = student. UNID
Joining tables in SQL • Cartesian product is built first • Then the results are restricted to only those rows that satisfy specified conditions – Example: All rows where Person. ID = Patient. ID

Join • Most powerful feature of relational system – Also the reason for performance problems! • Tables are joined in pairs – Select…. From Person p, Vitals v, Blood b Where p. pt_id = v. pt_id and p. pt_id = b. pt_id

Join • There are various types of joins, each subtly different. Some are more useful than others. • You don’t need to memorize the names, just try to get a feel for the concepts (we’ll do more when we work with SQL)

Theta Join • The tables must have a common attribute (doesn’t have to have the same name but must “mean” the same thing) • All attributes from student and class where ID matches

Theta Join • Theta is a comparison (X = Y and Z >1) • If the only comparison is =, it can also be called an equijoin • Natural join is an equijoin using all attributes from both tables

Outer Join • Join between R and S • Some of the rows in R do not have a corresponding row in S • Want all rows in R and the attributes from rows in S that match R • Missing values in S are set to null

Outer Join • Left: Keeps all of R and adds to S – Most common usage of outer join • Right: Keeps all of S and adds to R • Full: Keeps all of both – Although part of the relational algebra theory, full outer join may not be implemented in DBMS’s

Outer Join R ID 1 2 3 FN LN age Fred Smith 20 Joe Young 32 Sandy Jones 25 S ID student. Type 1 MS 3 BS Equijoin (inner join in SQL) returns rows 1 and 3. Outer join returns rows 1, 2, and 3. Student type is null for row 2.

Semi-join • All attributes of A that are in a row, such that the row can participate in an equi-join with B • Even though you are joining two relations, you only want to see the attributes of one relation Give me the name and age of all people who happen to also be students… name and age are both in the person table.

Division • Two relations. R (A 1, A 2, A 3, A 4, A 5) S (A 1, A 2, A 3) S is a subset of R • R/S will return attributes A 4, A 5 (the attributes that are NOT in subset S) for every row in R in which (A 1, A 2, A 3) matches a row in S Seldom, if ever, seen in an SQL statement.

Relational Calculus • Calculus refers to the addition of a predicate • Predicate is some qualifier that has a “truth value” (separate from the “join” statement) – True/False (… salary > $100, 000) – Is a member of… (… In (select ID from student)) • Returns those rows for which the predicate is true.

Relational Algebra and Calculus • A yardstick to compare a relational language (SQL variant) against • You make use of relational algebra and calculus when you query your database
- Slides: 42