Relational Algebra 2262021 DB Relational Algebra 1 Objectives

Relational Algebra 2/26/2021 DB: Relational Algebra 1

Objectives n n 2/26/2021 Introduction to Relational Algebra + Relational Algebra Operations + Summary + Example Queries + DB: Relational Algebra 2

- Introduction To Relational Algebra. . . n n n Relational algebra is a set of operations that enable the user to specify basic retrieval requests. Each operation produces results which is a relation. Relational algebra expression is a sequence of relational algebra operations whose result will also be a relation. There are two groups of relational algebra operations: n n 2/26/2021 Operations developed specifically for relational database, such as SELECT, PROJECT, and JOIN. Operations from mathematical set theory, such as UNION, SET DIFFERENCE, INTERSECTION, CARTESIAN PRODUCT, and DIVISION DB: Relational Algebra 3

… - Introduction To Relational Algebra n n n Set theoretic operations are used to merge the tuples of two relations. These are binary operations. Some set theoretic operations require both relations must be union compatible. Union compatible relations should have the same degree and each pair of corresponding attribute should have the same domain. These include: n n 2/26/2021 UNION SET DIFFERENCE INTERSECTION CARTESIAN PRODUCT is another set theoretic operation which doesn’t require union compatibility. DB: Relational Algebra 4

- Relational Algebra Operations n n n n 2/26/2021 Select + Project + Rename + Union + Difference + Intersection + Division + Assignment + Cartesian Product + Join + Outer Union + Composition of Operators + Aggregate Functions + Null Values + DB: Relational Algebra 5

-- Select Operation n n 2/26/2021 SELECT operation is used to select a subset of the tuples from the relation that satisfies the select condition. It is denoted by: p(r) p is called the selection predicate (SELECT condition) Defined as: p(r) = {t | t r and p(t)} Where p is a formula in propositional calculus consisting of terms connected by : (and), (or), (not) Each term is one of: <attribute> op <attribute> or <constant> where op is one of: =, , >, , <, Example of selection: T= name=“Adil” (EMPLOYEE) DB: Relational Algebra 6
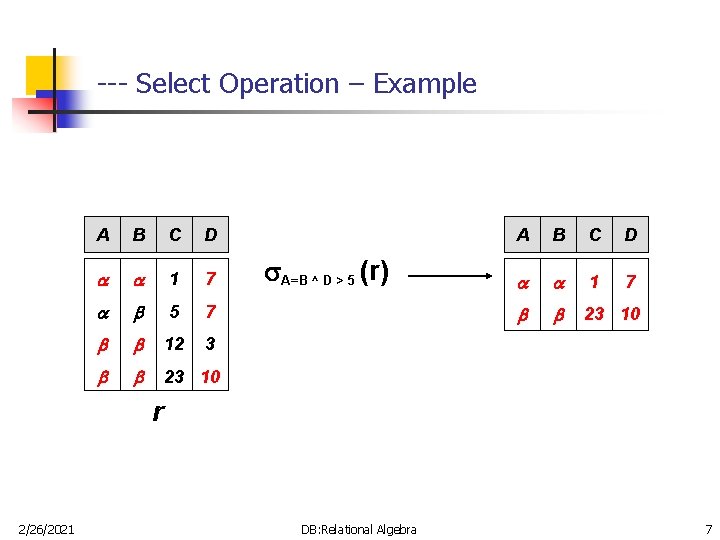
--- Select Operation – Example A B C D 1 7 5 7 12 3 23 10 A=B ^ D > 5 (r) A B C D 1 7 23 10 r 2/26/2021 DB: Relational Algebra 7

--- Characteristics of SELECT Operation n n n 2/26/2021 The select condition is applied independently to each tuple t in r. If the condition is true, then tuple t is selected and will appear in the resulting relation. The SELECT operation is unary, it is applied to a single relation. The degree of resulting relation is the same as r. The cardinality of resulting relation is less than or equal to r. The SELECT operation is cumulative. A sequence of SELECT operations can be applied in any order. n <cond 1>( <cond 2> (r)) = <cond 2>( <cond 1>(r)) A cascade of SELECT operations can be combined into a single SELECT operation with a conjunctive (^) condition. n <cond 1>(…( <condn> (r)) = <cond 1>^<cond 2> …<condn>(r) DB: Relational Algebra 8

-- Project Operation n Is used to select some attributes from a relation. n Is denoted by: <attribute list>(r) where <attribute list> are attribute names and r is a relation algebra expression n n The result is defined as the relation of <attribute list> columns obtained by erasing the columns that are not listed Example: To eliminate the name attribute of DEPARTMENT R = number (DEPARTMENT) 2/26/2021 DB: Relational Algebra 9
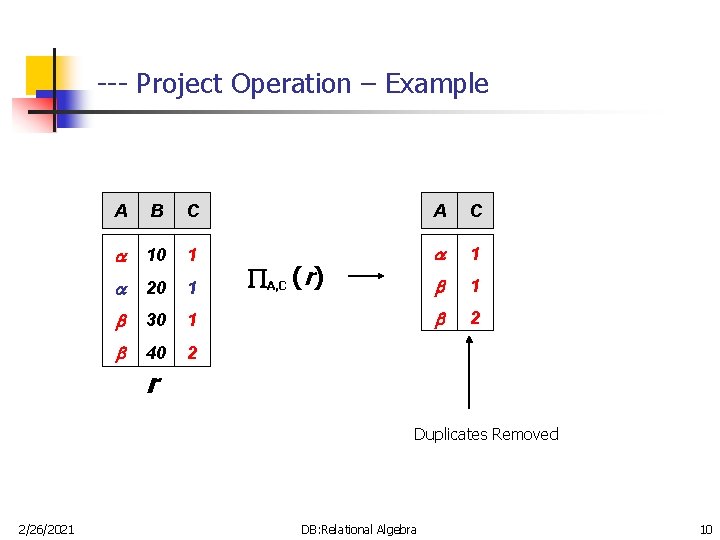
--- Project Operation – Example A B C A C 10 1 1 20 1 1 30 1 2 40 2 A, C (r) r Duplicates Removed 2/26/2021 DB: Relational Algebra 10

--- Characteristics of PROJECT Operation n The result of a PROJECT operation will be a relation consisting of the attributes specified in the <attribute list> in the same order. n The degree is equal to the number of attributes in the list. n The projection operations removes any duplicates. n n The cardinality of the resulting relation is always less than or equal to the cardinality of r. For a cascade of PROJECT operations, only the outermost need to be considered for evaluation. If <list 1> <list 2> … <listn> r, then n 2/26/2021 <list 1>( <list 2>(… ( <listn>(r))) = <list 1>(r) DB: Relational Algebra 11

-- Rename Operation n 2/26/2021 The rename operation ( ) allows us to name, and therefore to refer to, the results of relational-algebra expressions. Allows us to refer to a relation by more than one name. Example: s ( r) returns the expression r under the name s If a relational-algebra expression r has arity n, then s (A 1, A 2, …, An) (r) returns the result of expression r under the name s, and with the attributes renamed to A 1, A 2, …. , An. DB: Relational Algebra 12

Four Possible ways for Select and Project n Result=σ (emp) n Result = σ n Result = ∏ name, street (emp ) n Result = ∏ name, street (σ city = “Princeton” (emp) ) 2/26/2021 city = “Princeton” (emp) DB: Relational Algebra 13
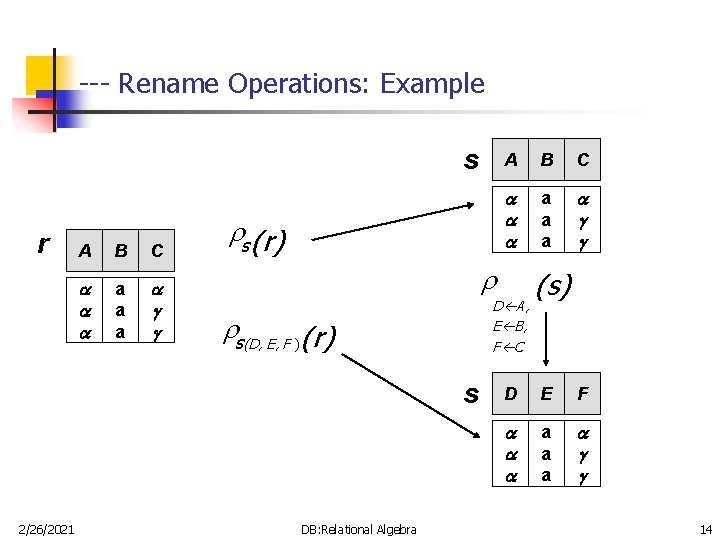
--- Rename Operations: Example s r A B C a a a s (r) B C a a a D A, E B, F C s(D, E, F ) (r) s 2/26/2021 A DB: Relational Algebra (s) D E F a a a 14

-- Union Operation n n n 2/26/2021 Is denoted by: r s Is defined as: r s = {t | t r or t s} The result of r s will include all tuples which are either in r or in s or in both. For r s to be valid r and s must be union compatible Union operation is: n Commutative: r s = s r n Associative: r (s w) = (r s) w E. g. to find all the names of faculty and students in the FACULTY and STUDENT tables: name (FACULTY) name (STUDENT) DB: Relational Algebra 15
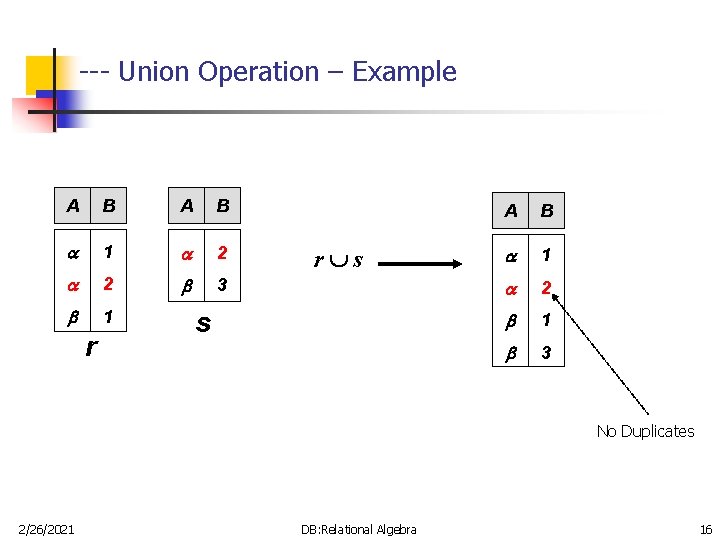
--- Union Operation – Example A B 1 2 2 3 1 r r s s A B 1 2 1 3 No Duplicates 2/26/2021 DB: Relational Algebra 16

-- Set Difference Operation n Is denoted by: r – s n IS defined as: r – s = {t | t r and t s} n n n 2/26/2021 The result of r – s will include all the tuples that are in r but not in s. r and s must be union compatible this operation is neither Commutative nor Associative. DB: Relational Algebra 17
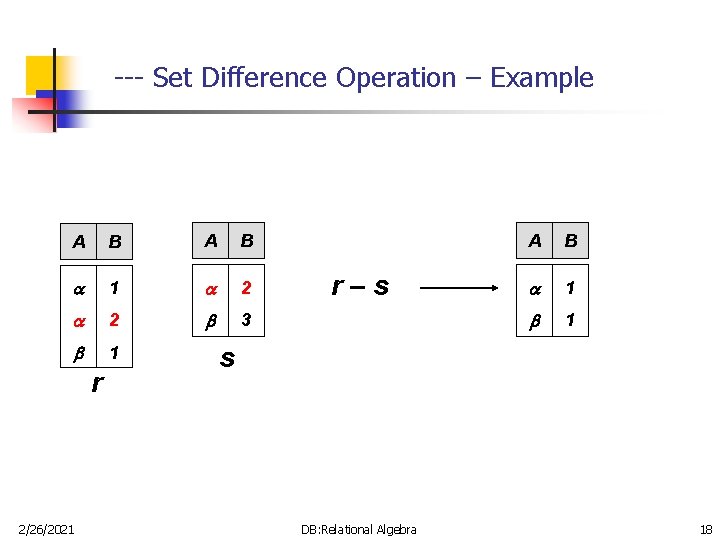
--- Set Difference Operation – Example A B 1 2 2 3 1 r 2/26/2021 r–s A B 1 1 s DB: Relational Algebra 18

-- Set-Intersection Operation n Is denoted by: r s n Is defined as: r s ={ t | t r and t s } n The result of r s will include all the tuples that are in both r and s. n r and s must be union compatible. n Intersection is: n n n 2/26/2021 Commutative: r s = s r Associative: r (s w) = (r s) w Note: r s = r - (r - s) DB: Relational Algebra 19
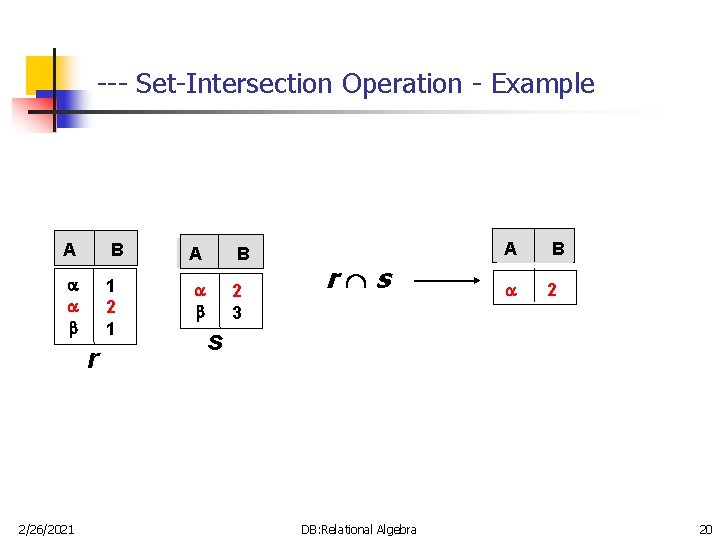
--- Set-Intersection Operation - Example A B 1 2 1 2 3 r 2/26/2021 r s A B 2 s DB: Relational Algebra 20

-- Division Operation … n Is denoted by: r s n Suited to queries that include the phrase “for all”. n Let r and s be relations on schemas R and S respectively where n R = (A , …, A , B , …, B ) 1 m 1 n n S = (B , …, B ) 1 n The result of r s is a relation on schema R – S = (A 1, …, Am) r s = { t | t R-S(r) u s ( tu r ) } 2/26/2021 DB: Relational Algebra 21
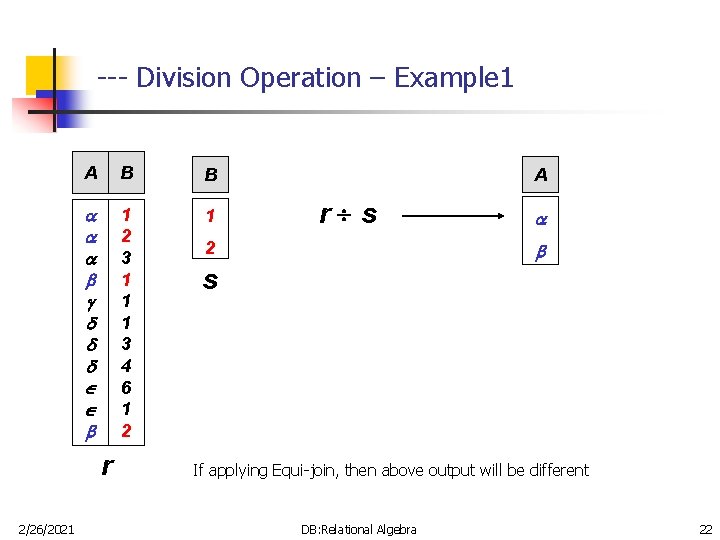
--- Division Operation – Example 1 A B B 1 2 3 1 1 1 3 4 6 1 2 1 r 2/26/2021 A r s 2 s If applying Equi-join, then above output will be different DB: Relational Algebra 22

--- Division Operations: Example 2 A B C D E a a a a a a b a b b 1 1 3 1 1 1 a b 1 1 r s s A B C a a r 2/26/2021 DB: Relational Algebra 23

… -- Division Operation n n Property n Let q = r s n Then q is the largest relation satisfying q x s r Definition in terms of the basic algebra operation Let r(R) and s(S) be relations, and let S R r s = R-S (r) – R-S ( ( R-S (r) x s) – R-S, S(r)) To see why n R-S, S(r) simply reorders attributes of r n R-S( R-S (r) x s) – R-S, S(r)) gives those tuples t in R-S (r) such that for some tuple u s, tu r. 2/26/2021 DB: Relational Algebra 24

-- Assignment Operation n The assignment operation ( ) provides a convenient way to express complex queries. n Write query as a sequential program consisting of n n a series of assignments followed by an expression whose value is displayed as a result of the query. Assignment must always be made to a temporary relation variable. Example: Write r s as temp 1 R-S (r) temp 2 R-S ((temp 1 x s) – R-S, S (r)) result = temp 1 – temp 2 n The result to the right of the is assigned to the relation variable on the left of the . n 2/26/2021 May use variable in subsequent expressions. DB: Relational Algebra 25
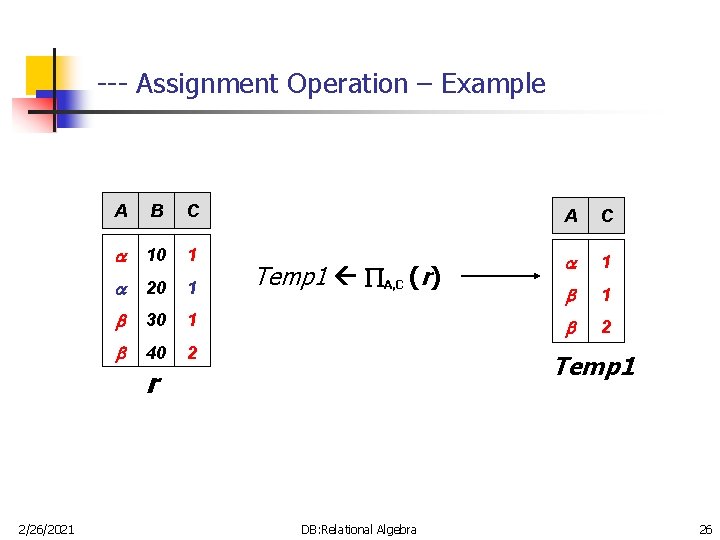
--- Assignment Operation – Example A B C A C 10 1 1 20 1 1 30 1 2 40 2 Temp 1 A, C (r) Temp 1 r 2/26/2021 DB: Relational Algebra 26

-- Cartesian-Product Operation n n 2/26/2021 Is denoted by: r x s Is defined as: r x s = {t q | t r and q s} The result of r x s will combine tuples from both r and s in a combinatorial fashion. Assume that attributes of r(A) and s(B) are disjoint. (That is, A B = ). If attributes of r(A) and s(B) are not disjoint, then renaming must be used. DB: Relational Algebra 27
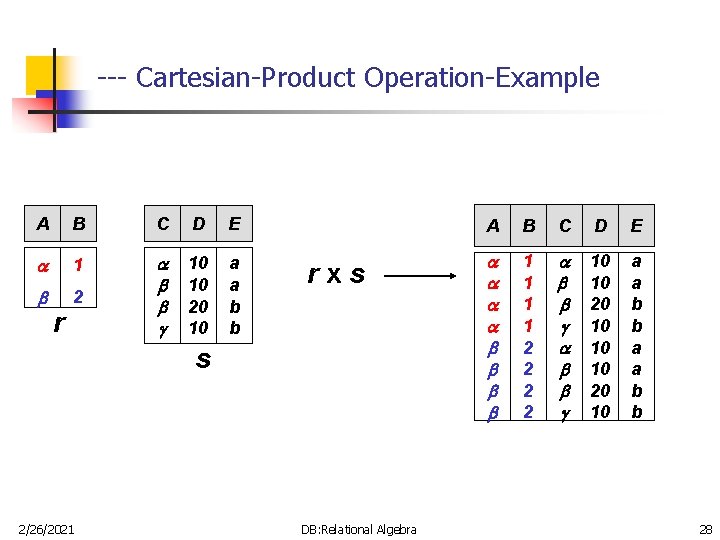
--- Cartesian-Product Operation-Example A B C D E 1 2 10 10 20 10 a a b b 1 1 2 2 10 10 20 10 a a b b r rxs s 2/26/2021 DB: Relational Algebra 28

--- Characteristics of Cartesian-Product Operation n 2/26/2021 Degree r X s = degree(r) + degree(s) Cardinality of r X s = cardinality(r) * cardinality(s) Generally the result of CARTESIAN PRODUCT is meaningless unless is followed by SELECT, and is called JOIN. DB: Relational Algebra 29

-- JOIN n n 2/26/2021 Join Operation combine related tuples from two relations into a single tuple based on join condition. Its is denoted by: r <join condition>s DB: Relational Algebra 30

--- Characteristic of the Join Operation n n 2/26/2021 Degree of the r s = degree(r) + degree(s). Cardinality of r cardinality(s). s is between 0 and cardinality (r) * The order of attributes in r s is { A 1, A 2, …, An, B 1, B 2, …, Bm} where A 1, A 2, …, An attributes of r and B 1, B 2, …, Bm are attributes of s. The resulting relation has one tuple for each combination of tuples – one from r and one for s – whenever the combination satisfies the join condition. DB: Relational Algebra 31

--- Types of Join Operation n n Theta join + Equijoin + Natural join + Outer Join + n n n 2/26/2021 Left Outer Join + Right Outer Join + Full Outer Join + DB: Relational Algebra 32
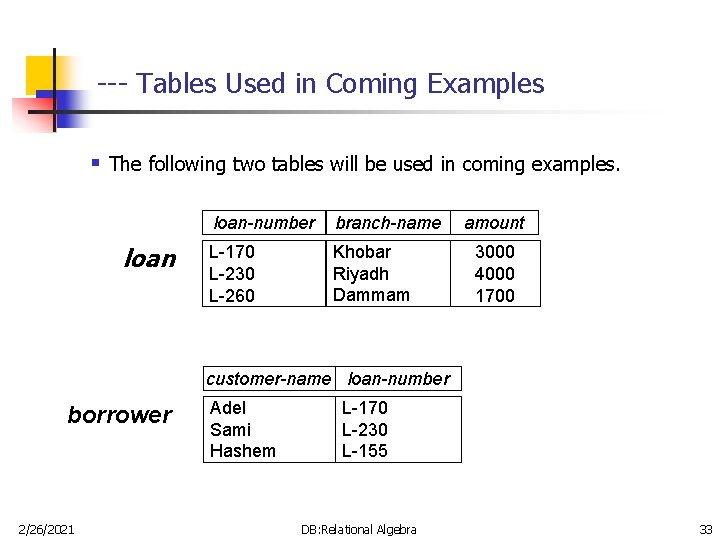
--- Tables Used in Coming Examples § The following two tables will be used in coming examples. loan-number branch-name L-170 L-230 L-260 Khobar Riyadh Dammam amount 3000 4000 1700 customer-name loan-number borrower 2/26/2021 Adel Sami Hashem L-170 L-230 L-155 DB: Relational Algebra 33

--- Theta Join Its is denoted by: r <r. A θ s. B> s Where θ = {=, ≠, < , >, ≤, ≥} n loan-number = loan-number Borrower Loan-number Branch-name amount Customer-name Loan-number L-170 Khobar 3000 Adel L-170 L-230 Riyadh 4000 Sami L-230 2/26/2021 DB: Relational Algebra 34

--- Equijoin n 2/26/2021 The most common join involves join conditions with equality comparisons, where θ is =. This special type of Theta join is called Equijoin. DB: Relational Algebra 35

--- Equijoin n n The most common join involves join conditions with equality comparisons, where θ is {=}. This special type of Theta join is called Equijoin. Its is denoted by: r loan <r. A = s. B> s loan-number = loan-number Borrower Loan-number Branch-name amount Customer-name Loan-number L-170 Khobar 3000 Adel L-170 L-230 Riyadh 4000 Sami L-230 § The problem with Equijoin is Pairs of attributes with identical values in evey tuple. 2/26/2021 DB: Relational Algebra 36

--- Natural-Join Operation n Is denoted by: r * s n Let r and s be relations on schemas R and S respectively. n 2/26/2021 Then, r * s is a relation on schema R S obtained as follows: n Consider each pair of tuples tr from r and ts from s. n If tr and ts have the same value on each of the attributes in R S, add a tuple t to the result, where n t has the same value as tr on r n t has the same value as ts on s Example: R = (A, B, C, D) S = (E, B, D) n Result schema = (A, B, C, D, E) n r * s is defined as: r. A, r. B, r. C, r. D, s. E ( r. B = s. B r. D = s. D (r x s)) DB: Relational Algebra 37
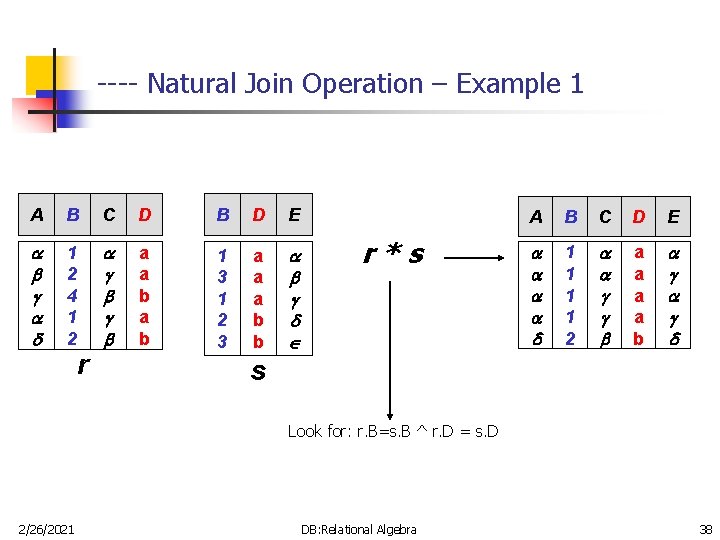
---- Natural Join Operation – Example 1 A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r r*s A B C D E 1 1 2 a a b s Look for: r. B=s. B ^ r. D = s. D 2/26/2021 DB: Relational Algebra 38

---- Natural Join – Example 2 loan * Borrower loan-number branch-name L-170 L-230 Khobar Riyadh amount 3000 4000 customer-name Adel Sami § Unlike Equijoin, no pairs of attributes with identical values in evey tuple. 2/26/2021 DB: Relational Algebra 39

--- Outer Join n An extension of the join operation that avoids loss of information. Computes the join and then adds tuples form one relation that does not match tuples in the other relation to the result of the join. Uses null values: n n null signifies that the value is unknown or does not exist All comparisons involving null are (roughly speaking) false by definition. n 2/26/2021 Will study precise meaning of comparisons with nulls later DB: Relational Algebra 40

---- Left Outer Join – Example loan-number L-170 L-230 L-260 2/26/2021 Borrower branch-name Khobar Riyadh Dammam amount 3000 4000 1700 DB: Relational Algebra customer-name Adel Sami null 41
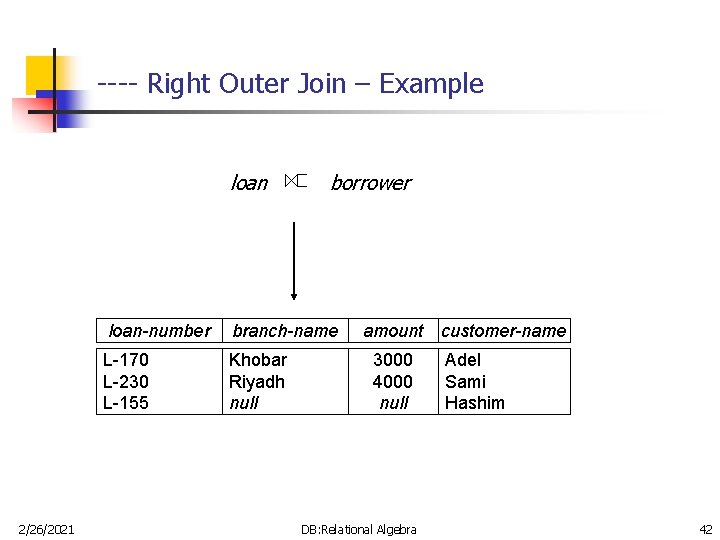
---- Right Outer Join – Example loan 2/26/2021 borrower loan-number branch-name L-170 L-230 L-155 Khobar Riyadh null amount 3000 4000 null DB: Relational Algebra customer-name Adel Sami Hashim 42
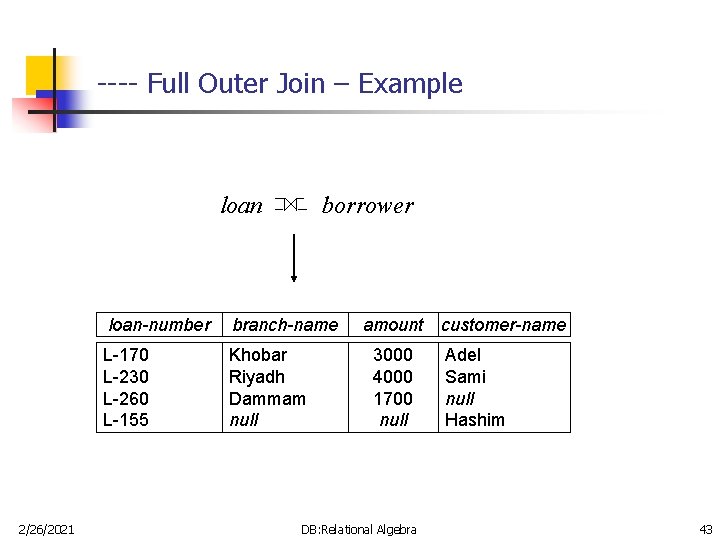
---- Full Outer Join – Example loan 2/26/2021 borrower loan-number branch-name L-170 L-230 L-260 L-155 Khobar Riyadh Dammam null amount 3000 4000 1700 null DB: Relational Algebra customer-name Adel Sami null Hashim 43

-- OUTER UNION Operation n n Outer Union operation compute the union of two relations if the relations are partially union compatible. Characteristics: n n n 2/26/2021 The list of compatible attributes includes a key for both relations. Tuples from the component relations with the same key are presented only once in the result and have values for all attributes in the result. The attributes that are not union compatible from either relation are kept in the result. Tuples that have no values for these attributes are padded with null values. OUTER UNION is equivalent to a FULL OUTER JOIN if the join attributes are all the common attributes of the two relations. DB: Relational Algebra 44
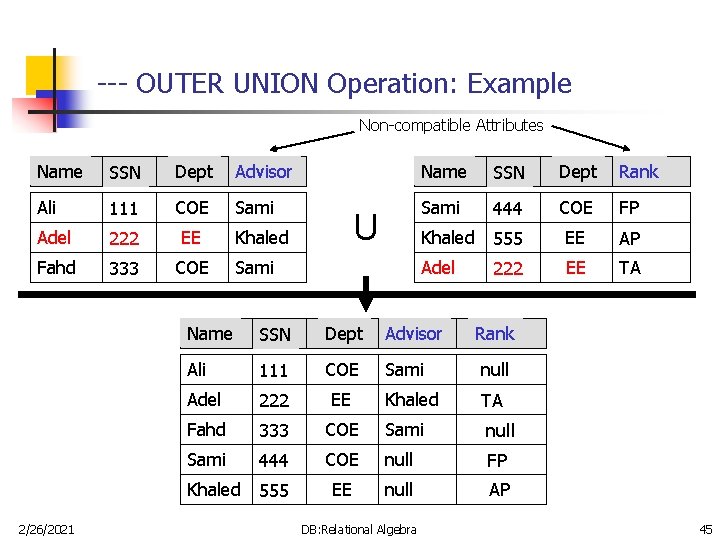
--- OUTER UNION Operation: Example Non-compatible Attributes Name SSN Dept Advisor Name SSN Dept Rank Ali 111 COE Sami 444 COE FP Adel 222 EE Khaled 555 EE AP Fahd 333 COE Adel 222 EE TA 2/26/2021 U Khaled Sami Name SSN Dept Advisor Ali 111 COE Sami null Adel 222 EE Khaled TA Fahd 333 COE Sami null Sami 444 COE null FP Khaled 555 EE null AP DB: Relational Algebra Rank 45
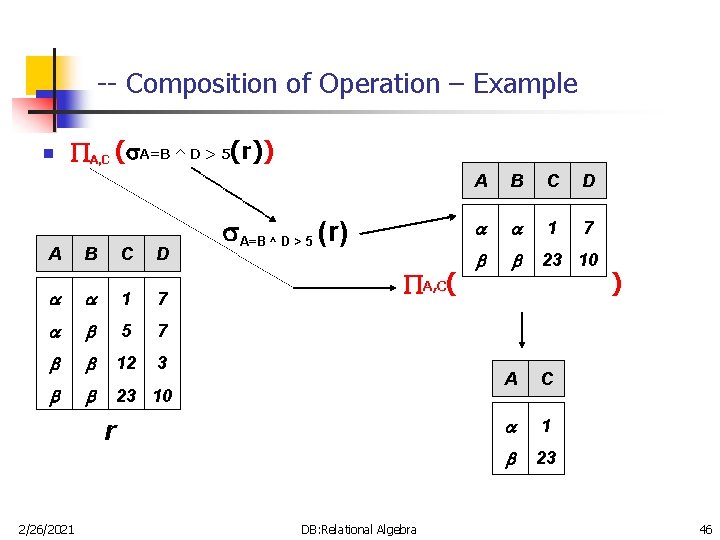
-- Composition of Operation – Example n A, C ( A=B ^ D > 5(r)) A B C D 1 7 5 7 12 3 23 10 A=B ^ D > 5 (r) A, C( r 2/26/2021 DB: Relational Algebra A B C D 1 7 23 10 A C 1 23 ) 46

-- Aggregate Functions and Operations n n Aggregation function takes a collection of values and returns a single value as a result. avg: average value min: minimum value max: maximum value sum: sum of values count: number of values Aggregate operation in relational algebra G 1, G 2, …, Gn g F 1( A 1), F 2( A 2), …, Fn( An) (E) n n 2/26/2021 E is any relational-algebra expression G 1, G 2 …, Gn is a list of attributes on which to group (can be empty) Each Fi is an aggregate function Each Ai is an attribute name DB: Relational Algebra 47
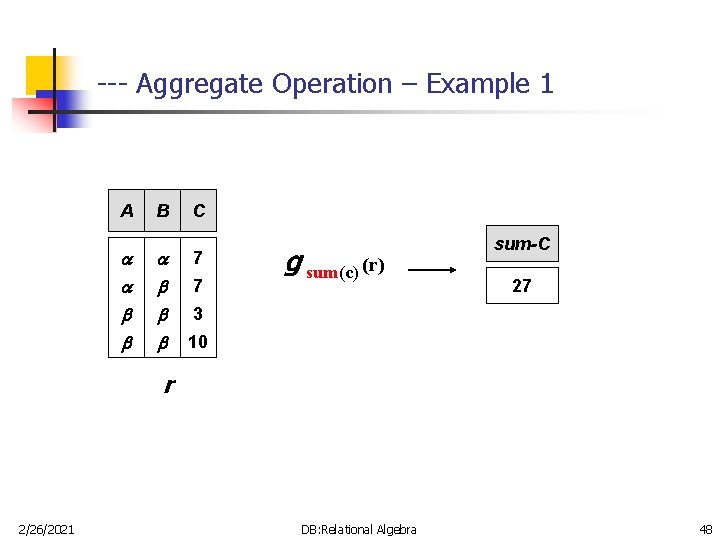
--- Aggregate Operation – Example 1 A B C 7 7 g sum(c) (r) sum-C 27 3 10 r 2/26/2021 DB: Relational Algebra 48
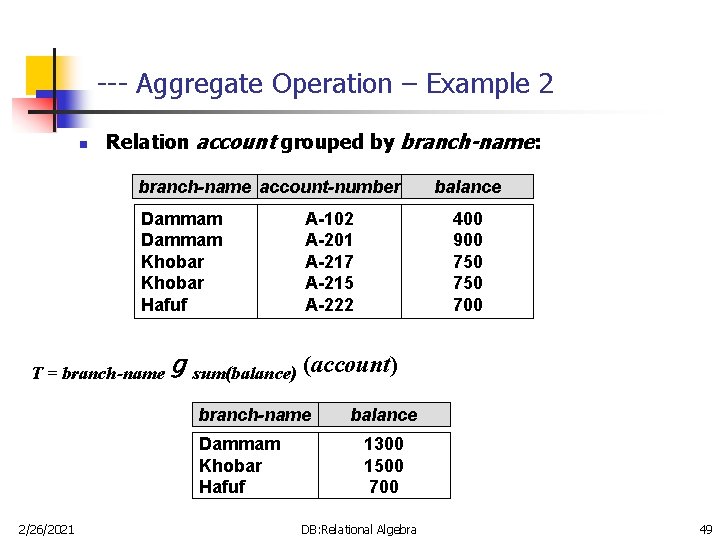
--- Aggregate Operation – Example 2 n Relation account grouped by branch-name: branch-name account-number Dammam Khobar Hafuf T = branch-name A-102 A-201 A-217 A-215 A-222 400 900 750 700 g sum(balance) (account) branch-name Dammam Khobar Hafuf 2/26/2021 balance 1300 1500 700 DB: Relational Algebra 49

--- Aggregate Functions: Renaming n Result of aggregation does not have a name n n Can use rename operation to give it a name For convenience, we permit renaming as part of aggregate operation branch-name 2/26/2021 g sum(balance) as sum-balance (account) DB: Relational Algebra 50

-- Null Values … n n It is possible for tuples to have a null value, denoted by null, for some of their attributes null signifies an unknown value or that a value does not exist. The result of any arithmetic expression involving null is null. Aggregate functions simply ignore null values n n n For duplicate elimination and grouping, null is treated like any other value, and two nulls are assumed to be the same n n 2/26/2021 Is an arbitrary decision. Could have returned null as result instead. We follow the semantics of SQL in its handling of null values Alternative: assume each null is different from each other Both are arbitrary decisions, so we simply follow SQL DB: Relational Algebra 51

… -- Null Values n Comparisons with null values return the special truth value unknown n n 2/26/2021 not (A < 5) A >= 5 Three-valued logic using the truth value unknown: n n If false was used instead of unknown, then would not be equivalent to OR: (unknown or true) = true, (unknown or false) = unknown (unknown or unknown) = unknown AND: (true and unknown) = unknown, (false and unknown) = false, (unknown and unknown) = unknown NOT: (not unknown) = unknown In SQL “P is unknown” evaluates to true if predicate P evaluates to unknown Result of select predicate is treated as false if it evaluates to unknown DB: Relational Algebra 52
- Summary … 2/26/2021 DB: Relational Algebra 53
… - Summary … 2/26/2021 DB: Relational Algebra 54
… - Summary n n n n n 2/26/2021 Select Project Rename Union Difference Intersection Division Assignment Cartesian Product – X n n n Join Natural Join Left Outer Join Right Outer Join Full Outer Join Aggregate Function DB: Relational Algebra * g 55

- Example Queries … n The following Relations are used for the coming Examples. n branch (branch-name, branch-city, assets) n customer (customer-name, customer-street, customer-only) n account (account-number, branch-name, balance) n loan (loan-number, branch-name, amount) n depositor (customer-name, account-number) n borrower (customer-name, loan-number) 2/26/2021 DB: Relational Algebra 56

… - Example Queries … n Find all loans of over $1200 T = amount > 1200 (loan) n Find the loan number for each loan of an amount greater than $1200 T = loan-number ( amount > 1200 (loan)) 2/26/2021 DB: Relational Algebra 57

… - Example Queries … Find the names of all customers who have a loan, an account, or both, from the bank n T = customer-name (borrower) customer-name (depositor) n Find the names of all customers who have a loan and an account at bank T = customer-name (borrower) customer-name (depositor) 2/26/2021 DB: Relational Algebra 58

… - Example Queries … Find the names of all customers who have a loan at the KFUPM branch. n T = customer-name ( branch-name=“KFUPM” ( borrower. loan-number = loan-number(borrower * loan))) Find the of all customers who have a loan at the KFUPM branch but do not have an account at any branch of the bank n T = customer-name ( branch-name = “KFUPM” ( borrower. loan-number = loan-number(borrower customer-name(depositor) 2/26/2021 DB: Relational Algebra * loan))) – 59

… - Example Queries … n Find the names of all customers who have a loan at the KFUPM branch. Query 1 T = customer-name( branch-name = “KFUPM” ( borrower. loan-number = loan-number(borrower * loan))) Query 2 T = customer-name( loan-number = borrower. loan-number( ( branch-name = “KFUPM”(loan)) * borrower)) 2/26/2021 DB: Relational Algebra 60

… - Example Queries … Find the largest account balance. Rename account relation as d n T = balance(account) - account. balance ( account. balance < d. balance (account X d (account))) 2/26/2021 DB: Relational Algebra 61

… - Example Queries … n Find all customers who have an account from at least the “Dammam” and the “Khobar” branches. Query 1 T= CN( BN=“Dammam”(depositor * account)) CN( BN=“Khobar”(depositor * account)) where CN denotes customer-name and BN denotes branch-name. Query 2 T = customer-name, branch-name (depositor * account) temp(branch-name) ({(“Dammam”), (“Khobar”)}) 2/26/2021 DB: Relational Algebra 62

… - Example Queries n Find all customers who have an account at all branches located in Dammam city. T = customer-name, branch-name (depositor * account) branch-name ( branch-city = “Dammam” (branch)) 2/26/2021 DB: Relational Algebra 63
- Slides: 63