Relational Algebra Relational Algebra Formalism for creating new

Relational Algebra
Relational Algebra • Formalism for creating new relations from existing ones • Its place in the big picture: Declartive query language SQL, relational calculus Algebra Relational algebra Relational bag algebra Implementation

Relational Algebra • Five operators: – – – Union: Difference: Selection: s Projection: P Cartesian Product: • Derived or auxiliary operators: – Intersection, complement – Joins (natural, equi-join, theta join, semi-join) – Renaming: r

1. Union and 2. Difference • R 1 R 2 • Example: – Active. Employees Retired. Employees • R 1 – R 2 • Example: – All. Employees -- Retired. Employees

What about Intersection ? • • It is a derived operator R 1 R 2 = R 1 – (R 1 – R 2) Also expressed as a join (will see later) Example – Unionized. Employees Retired. Employees

3. Selection • Returns all tuples which satisfy a condition • Notation: sc(R) • Examples – s. Salary > 40000 (Employee) – sname = “Smithh” (Employee) • The condition c can be =, <, , >, , <>

Find all employees with salary more than $40, 000. s Salary > 40000 (Employee)

4. Projection • Eliminates columns, then removes duplicates • Notation: P A 1, …, An (R) • Example: project social-security number and names: – P SSN, Name (Employee) – Output schema: Answer(SSN, Name)
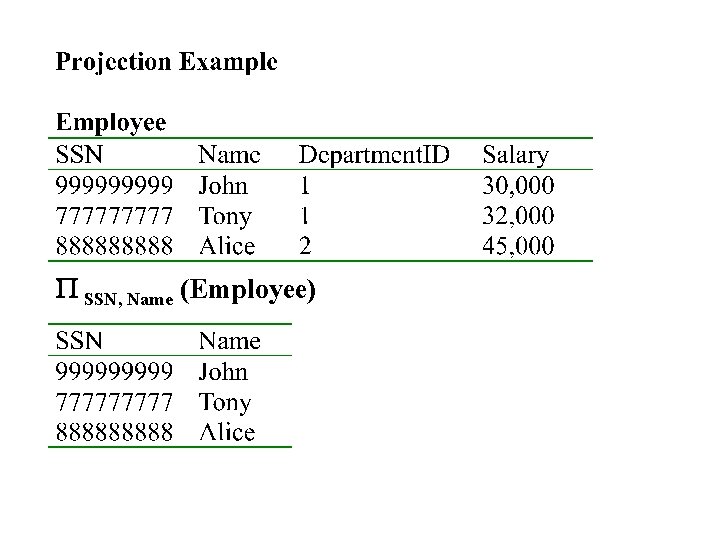
P SSN, Name (Employee)

5. Cartesian Product • Each tuple in R 1 with each tuple in R 2 • Notation: R 1 R 2 • Example: – Employee Dependents • Very rare in practice; mainly used to express joins


Relational Algebra • Five operators: – – – Union: Difference: Selection: s Projection: P Cartesian Product: • Derived or auxiliary operators: – Intersection, complement – Joins (natural, equi-join, theta join, semi-join) – Renaming: r

Renaming • Changes the schema, not the instance • Notation: r B 1, …, Bn (R) • Example: – r. Last. Name, Soc. No (Employee) – Output schema: Answer(Last. Name, Soc. No)

Renaming Example Employee Name John Tony r. Last. Name, Soc. No Last. Name John Tony SSN 99999 77777 (Employee) Soc. No 99999 77777

Natural Join • Notation: R 1 ⋈ R 2 • Meaning: R 1 ⋈ R 2 = PA(s. C(R 1 R 2)) • Where: – The selection s. C checks equality of all common attributes – The projection eliminates the duplicate common attributes

Natural Join Example Employee Name John Tony SSN 99999 77777 Dependents SSN 99999 77777 Dname Emily Joe Employee Dependents = PName, SSN, Dname(s SSN=SSN 2(Employee x r. SSN 2, Dname(Dependents)) Name John Tony SSN 99999 77777 Dname Emily Joe
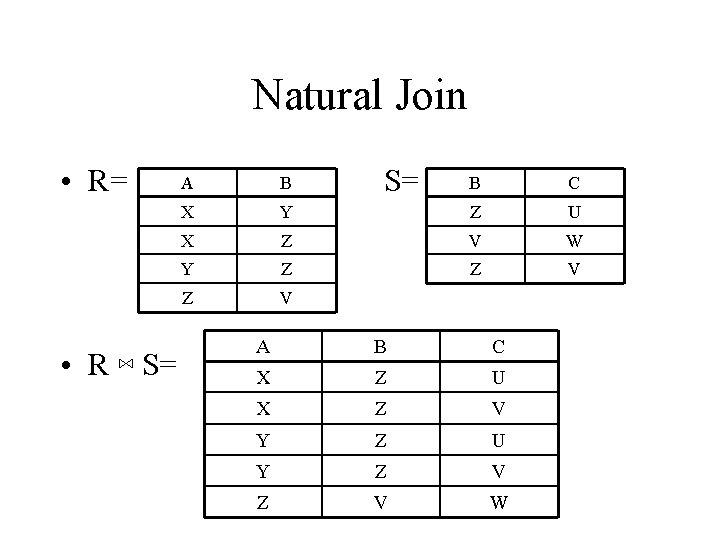
Natural Join • R= • R ⋈ S= A B X S= B C Y Z U X Z V W Y Z Z V A B C X Z U X Z V Y Z U Y Z V W

Natural Join • Given the schemas R(A, B, C, D), S(A, C, E), what is the schema of R ⋈ S ? • Given R(A, B, C), S(D, E), what is R ⋈ S ? • Given R(A, B), S(A, B), what is R ⋈ S ?

Theta Join • A join that involves a predicate • R 1 ⋈ q R 2 = s q (R 1 R 2) • Here q can be any condition

Eq-join • A theta join where q is an equality • R 1 ⋈A=B R 2 = s A=B (R 1 R 2) • Example: – Employee ⋈SSN=SSN Dependents • Most useful join in practice

Semijoin • R ⋉ S = P A 1, …, An (R ⋈ S) • Where A 1, …, An are the attributes in R • Example: – Employee ⋉ Dependents
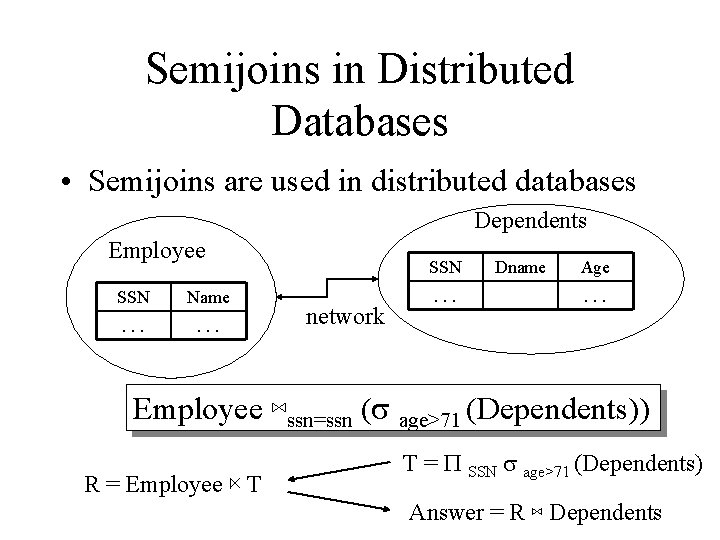
Semijoins in Distributed Databases • Semijoins are used in distributed databases Dependents Employee SSN Name . . . SSN network . . . Dname Age. . . Employee ⋈ssn=ssn (s age>71 (Dependents)) R = Employee ⋉ T T = P SSN s age>71 (Dependents) Answer = R ⋈ Dependents
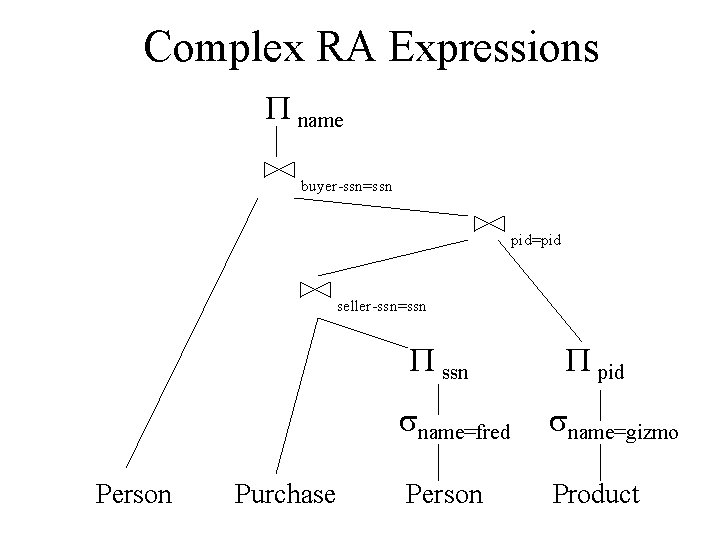
Complex RA Expressions P name buyer-ssn=ssn pid=pid seller-ssn=ssn Person Purchase P pid sname=fred sname=gizmo Person Product

Operations on Bags A bag = a set with repeated elements All operations need to be defined carefully on bags • {a, b, b, c} {a, b, b, b, e, f, f}={a, a, b, b, b, c, e, f, f} • {a, b, b, b, c, c} – {b, c, c, c, d} = {a, b, b, d} • s. C(R): preserve the number of occurrences • PA(R): no duplicate elimination • Cartesian product, join: no duplicate elimination Important ! Relational Engines work on bags, not sets ! Reading assignment: 5. 3 – 5. 4

Finally: RA has Limitations ! • Cannot compute “transitive closure” Name 1 Name 2 Relationship Fred Mary Father Mary Joe Cousin Mary Bill Spouse Nancy Lou Sister • Find all direct and indirect relatives of Fred • Cannot express in RA !!! Need to write C program
- Slides: 25












































