Relational Algebra Chapter 4 part I Relational Query

Relational Algebra Chapter 4 - part I

Relational Query Languages v Query languages: Allow manipulation and retrieval of data from a database. v Relational model supports simple powerful QLs: § § v Strong formal foundation based on logic. Allows for much optimization. Query Languages != Programming languages! § § § QLs not expected to be “Turing complete”. QLs not intended to be used for complex calculations. QLs support easy, efficient access to large data sets. 2

Formal Relational Query Languages q Two mathematical Query Languages form the basis for “real” languages (e. g. SQL) and for implementation: q Relational Algebra: q. More operational, very useful for representing execution plans. q Relational Calculus: q. Lets users describe what they want, rather than how to compute it. (Non-operational, rather declarative. ) 3

Preliminaries A query is applied to relation instances. v The result of a query is also a relation instance. v § Schemas of input relations for a query are fixed ; (but query will run regardless of instance!) § The schema for result of given query is also fixed! Determined by definition of query language. 4

Preliminaries v Positional vs. named-field notation: § Positional field notation e. g. , S. 1 § Named field notation e. g. , v S. sid Pros/Cons: § Positional notation easier formal definitions, named-field notation more readable. § Both used in SQL v. Assume that names of fields in query results are `inherited’ from names of fields in query input relations. 5

Example Instances Sailors Reserves R 1 Sailors S 2 6

Relational Algebra v Basic operations: § § § v Additional operations: § v Selection ( ) Selects a subset of rows from relation. Projection ( ) Deletes unwanted columns from relation. Cartesian-product ( ) Allows us to combine two relations. Set-difference ( ) Tuples in reln. 1, but not in reln. 2. Union ( ) Tuples in reln. 1 and in reln. 2. Intersection, join, division, renaming: Not essential, but (very!) useful. Since each operation returns a relation, operations can be composed! (Algebra is “closed”. ) 7
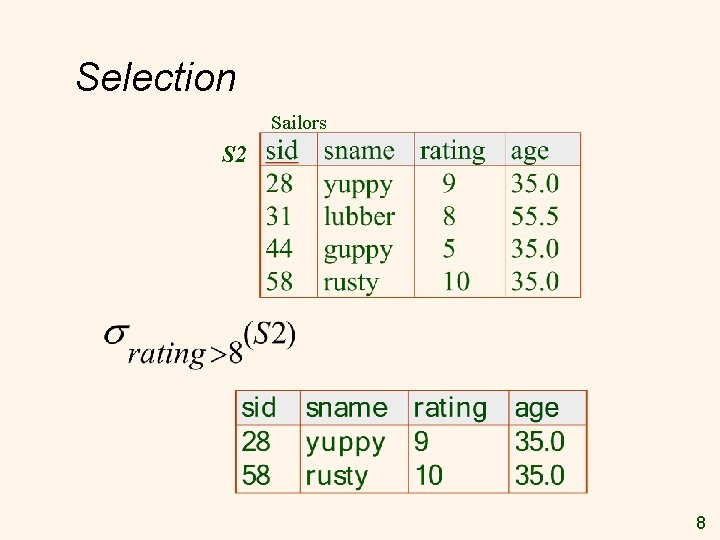
Selection Sailors S 2 8

Selection v v condition (R) Selects rows that satisfy selection condition. attribute op constant attribute op attribute Op is {<, >, <=, >=, =, =} v v No duplicates in result! Schema of result identical to schema of (only) input relation. 9
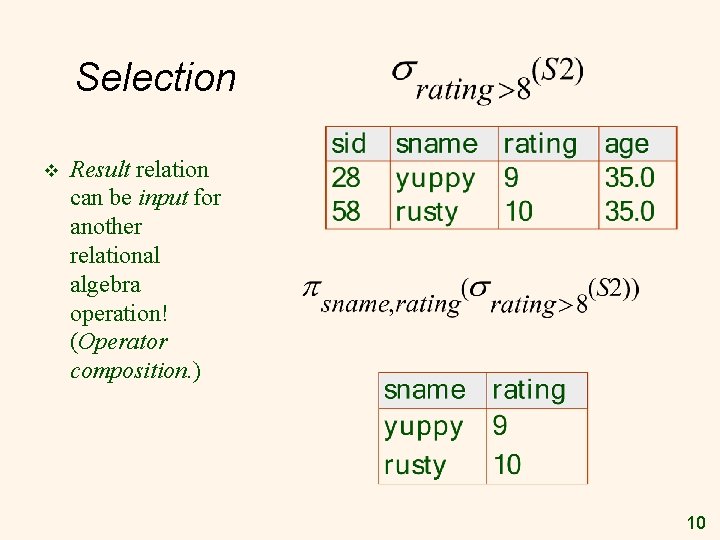
Selection v Result relation can be input for another relational algebra operation! (Operator composition. ) 10

Projection Sailors S 2 11

Projection v projectlist (R) v Deletes attributes that are not in projection list. Schema of result = contains fields in projection list Projection operator has to eliminate duplicates! (Why? ? ) § Note: real systems typically don’t do duplicate elimination unless the user explicitly asks for it. (Why not? ) v v 12

Union, Intersection, Set. Difference v All of these operations take two input relations, which must be union-compatible: § § v Same number of fields. `Corresponding’ fields have same type. What is the schema of result? 13
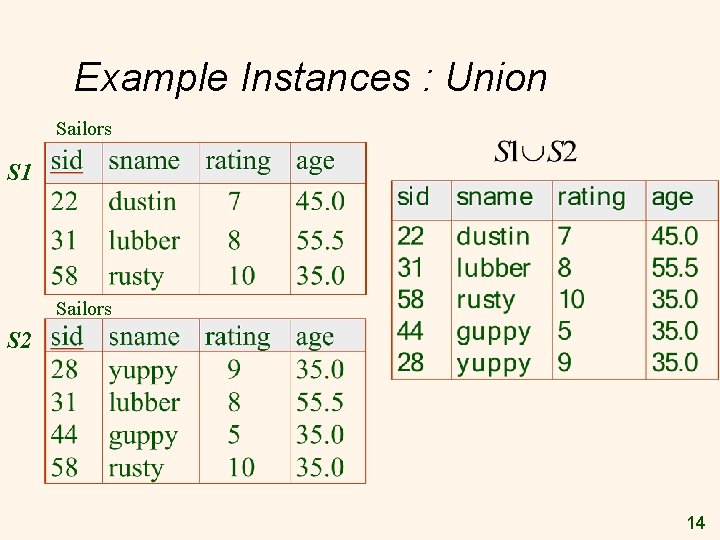
Example Instances : Union Sailors S 1 Sailors S 2 14

Difference Operation Sailors S 1 Sailors S 2 16

Intersection Operation Sailors S 1 Sailors S 2 18

Cross-Product (Cartesian Product) v S 1 R 1 : Each row of S 1 is paired with each row of R 1. Reserves R 1 Sailors S 1 20

Cross-Product (Cartesian Product) S 1 R 1 : Result schema has one field per field of S 1 and R 1, v with field names `inherited’ if possible. § Conflict: Both S 1 and R 1 have a field called sid. * Renaming operator: 21

Why we need a Join Operator ? § In many cases, Join = Cross-Product + Select + Project § However : Cross-product is too large to materialize Apply Select and Project "On-the-fly" 22

Condition Join / Theta Join v Condition Join: v Result schema same as that of cross-product. Fewer tuples than cross-product, more efficient. v 23

Equi. Join v Equi-Join: A special case of condition join where the condition c contains only equalities. Result schema similar to cross-product, but only one copy of fields for which equality is specified. v An extra project: PROJECT ( THETA-JOIN) v 24

Natural Join v Natural Join: Equijoin on all common fields. 25

Division v Not supported as a primitive operator, useful for expressing queries like: but Find sailors who have reserved all boats. § Example : “Reservations / Boats ” 26

Division v Let A have 2 fields x and y; B have only field y: § A/B = v A/B contains all x tuples (sailors) such that for every y tuple (boat) in B, there is an xy tuple in A. 27

Division Example e. g. , A= B= A/B = the Supplies relation for all parts supplied by suppliers, the Parts relation suppliers who supply all parts listed in B 28

Examples of Division A/B B 1 B 2 B 3 A A/B 1 A/B 2 A/B 3 29

Expressing A/B Using Basic Operators v Idea: For A/B, compute all x values that are not `disqualified’ by some y value in B. § x is disqualified if by attaching y value from B, we obtain an xy tuple that is not in A. Disqualified x values: A/B: 30

A few example queries 31

Find names of sailors who’ve reserved boat #103 Solution 1 Solution 2 Solution 3 32
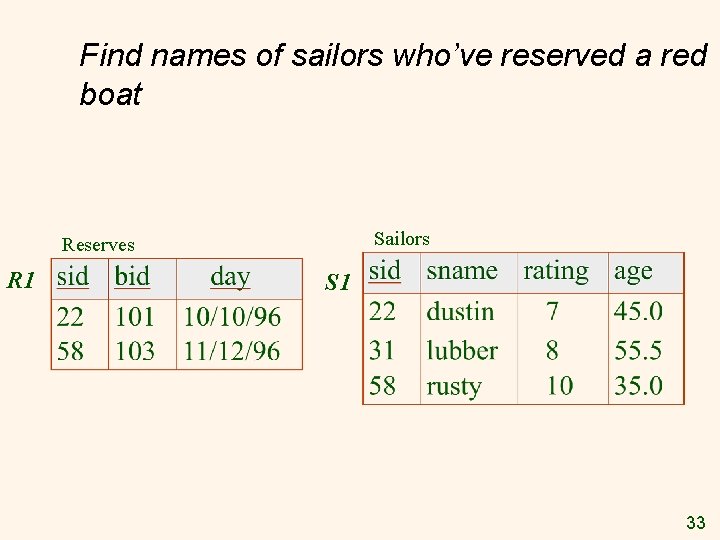
Find names of sailors who’ve reserved a red boat Sailors Reserves R 1 S 1 33

Find names of sailors who’ve reserved a red boat v Information about boat color only available in Boats; so need an extra join: A more efficient solution: * A query optimizer can find this given the first solution! 34

Find sailors who’ve reserved a red or a green boat v Can identify all red or green boats, then find sailors who’ve reserved one of these boats: Can also define Tempboats using union! (How? ) What happens if is replaced by in this query? 35

Find sailors who’ve reserved a red and a green boat Previous approach won’t work! v Must identify sailors who reserved red boats, sailors who’ve reserved green boats, then find their intersection v 36

Find the names of sailors who’ve reserved all boats v v Uses division; schemas of the input relations to / must be carefully chosen: To find sailors who’ve reserved all ‘Interlake’ boats: . . . 37

Relational Algebra : Some More Operators Beyond Chapter 4

Generalized Projection sname, (ratings * 2 as myratings) ( Sailors ) 39

Aggregation Use G operator to indicate application of an aggregate function; only one result tuple is being returned. §COUNT (*) §COUNT ( [DISTINCT] A) §SUM ( [DISTINCT] A) §AVG ( [DISTINCT] A) §MAX (A) §MIN (A) 40

Aggregate Operator on Whole Relation Example: G G sum (rating) as myrating … ( sum-DISTINCT Sailor ) (rating) … ( Sailor ) 41

Find name and age of the oldest sailor(s) Example: Rename ( Tmp 1, G max (rating) as max-age ( Sailor )) Project [sname, sage] ( Tmp 1 JOIN[maxage, age] Sailor ) Or Project [sname, sage] ( SELECT [age IN Tmp 1] Sailor ) 42

Find name and age of the oldest sailor(s) v So far, aggregate operators to all (qualifying) tuples. v Question: § What if want to apply aggregate to each group of tuples ? v Example : § Find the age of the youngest sailor for each rating level. v Example Procedure : § Suppose rating values {1, 2, …, 10}, 10 queries: § For i = 1, 2, . . . , 10: G[min(sage); rating] (Select[S. rating=i] (Sailors)) 43

Aggregate Operator G on Groups We can also use the G operator to indicate first partitioning of the relation into groups, and then application of aggregate function to each group. Then one result tuple is being returned per group. G [age] [ sum (rating) as sum-rating ] ( Sailor ) 44

Running Example v Instances of the Sailors and Reserves relations in our examples. §R 1 §S 2 45

Motivation for Grouping §For i = 1, 2, . . . , 10: § §SELECT MIN (S. age) §FROM Sailors S §WHERE S. rating = i What are the problems with above ? • We may not know how many rating levels exist. • Nor what the rating values for these levels are. • Performance issue (why ? ) 46

Running Example v Instances of the Sailors and Reserves relations in our examples. §R 1 §S 2 47

Find age of the youngest sailor with age 18, for each rating with at least 2 such sailors PROJECT[min-age]( SELECT[s-count > 1] ( G[S. rating][count(*) -> s-count; min(S. age) as min-age ] (SELECT[S. age>=18](Sailors)))) 48

Find age of the youngest sailor with age 18, for each rating with at least 2 such sailors §Sailors instance: 49
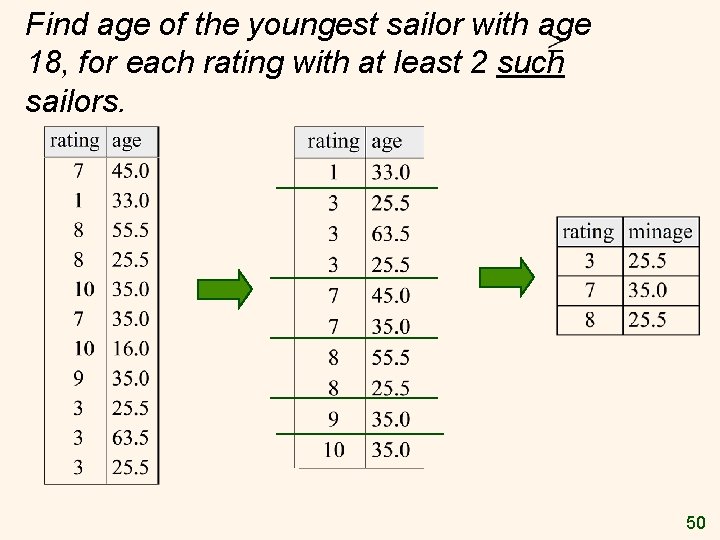
Find age of the youngest sailor with age 18, for each rating with at least 2 such sailors. 50

Summary v The relational model has rigorously defined query languages that are simple and powerful. v Relational algebra is operational; useful as internal representation for query evaluation plans. v Several ways of expressing a given query; a query optimizer should choose most efficient version. 51
- Slides: 48