Relational Algebra continued Lecture 5 Relational Algebra Summary

Relational Algebra (continued) Lecture 5

Relational Algebra (Summary) • Basic operations: – – – Selection ( ) Selects a subset of rows from relation. Projection ( ) Deletes unwanted columns from relation. Cross-product ( ) Allows us to combine two relations. Set-difference ( - ) Tuples in reln. 1, but not in reln. 2. Union ( ) Tuples either in reln. 1 or in reln. 2 or in both. Rename ( ) Changes names of the attributes • Since each operation returns a relation, operations can be composed ! (Algebra is “closed”. ) • Use of temporary relations recommended.

Additional operators We define additional operations that do not add any power to the relational algebra, but that simplify common queries. – Natural join – Conditional Join – Equi-Join – Division All joins are really special cases of conditional join Also, we’ve already seen “Set intersection”: r s = r - (r - s) 3

Quick note on notation bad_customers good_customers customer-name loan-number Patty 1234 Seymour 3432 Apu 3421 Marge 3467 Selma 2342 Selma 7625 Ned 4531 Abraham 3597 If we have two or more relations which feature the same attribute names, we could confuse them. To prevent this we can use dot notation. For example good_customers. loan-number 4

Natural-Join Operation: Motivation Very often, we have a query and the answer is not contained in a single relation. For example, I might wish to know where Apu banks. The classic relational algebra way to do such queries is a cross product, followed by a selection which tests for equality on some pair of fields. borrower cust-name l-number branch Patty 1234 Dublin Apu 3421 Irvine borrower. l-number = loan. l-number(borrower x loan))) While this works… • it is unintuitive • it requires a lot of memory • the notation is cumbersome loan cust-name borrower. l-number loan. l-number branch Patty 1234 Dublin Patty 1234 3421 Irvine Apu 3421 1234 Dublin Apu 3421 Irvine cust-name borrower. l-number loan. l-number branch Patty 1234 Dublin Apu 3421 Irvine Note that in this example the two relations are the same size (2 by 2), this does not have to be the case. So, we have a more intuitive way of achieving the same effect, the natural join, denoted by the symbol 5

Natural-Join Operation: Intuition Natural join combines a cross product and a selection into one operation. It performs a selection forcing equality on those attributes that appear in both relation schemes. Duplicates are removed as in all relation operations. For the previous example (one attribute in common: “l-number”), we have… borrower loan = borrower. l-number = loan. l-number(borrower x loan))) • If the two relations have no attributes in common, then their natural join is simply their cross product. • If the two relations have more than one attribute in common, then the natural join selects only the rows where all pairs of 6 matching attributes match. (let’s see an example on the next slide).
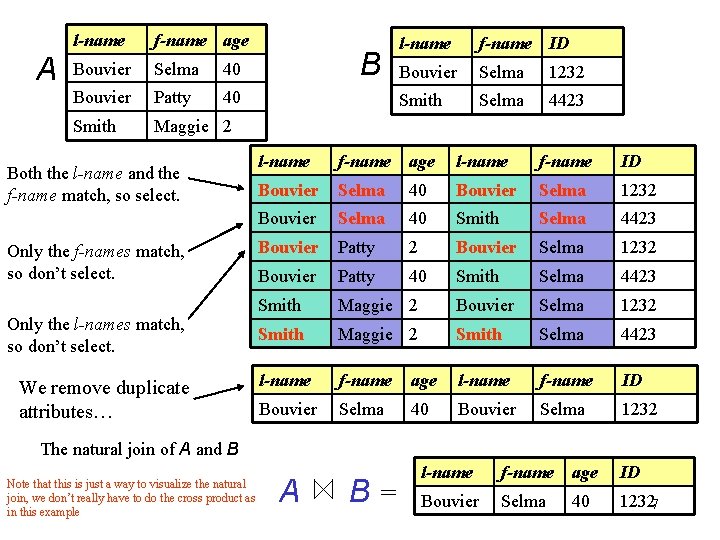
A l-name f-name age Bouvier Selma 40 Bouvier Patty 40 Smith Maggie 2 Both the l-name and the f-name match, so select. Only the f-names match, so don’t select. Only the l-names match, so don’t select. We remove duplicate attributes… B l-name f-name ID Bouvier Selma 1232 Smith Selma 4423 l-name f-name age l-name f-name ID Bouvier Selma 40 Bouvier Selma 1232 Bouvier Selma 40 Smith Selma 4423 Bouvier Patty 2 Bouvier Selma 1232 Bouvier Patty 40 Smith Selma 4423 Smith Maggie 2 Bouvier Selma 1232 Smith Maggie 2 Smith Selma 4423 l-name f-name age l-name f-name ID Bouvier Selma 40 Bouvier Selma 1232 The natural join of A and B Note that this is just a way to visualize the natural join, we don’t really have to do the cross product as in this example A B= l-name f-name age ID Bouvier Selma 40 12327

Natural-Join Operation • Notation: r s • Let r and s be relation instances on schemas R and S respectively. The result is a relation on schema R S which is obtained by considering each pair of tuples tr from r and ts from s. • If tr and ts have the same value on each of the attributes in R S, a tuple t is added to the result, where – t has the same value as tr on r – t has the same value as ts on s • Example: R = (A, B, C, D) S = (E, B, D) • Result schema = (A, B, C, D, E) • r s is defined as: r. A, r. B, r. C, r. D, s. E ( r. B = s. B r. D = s. D (r x s)) 8
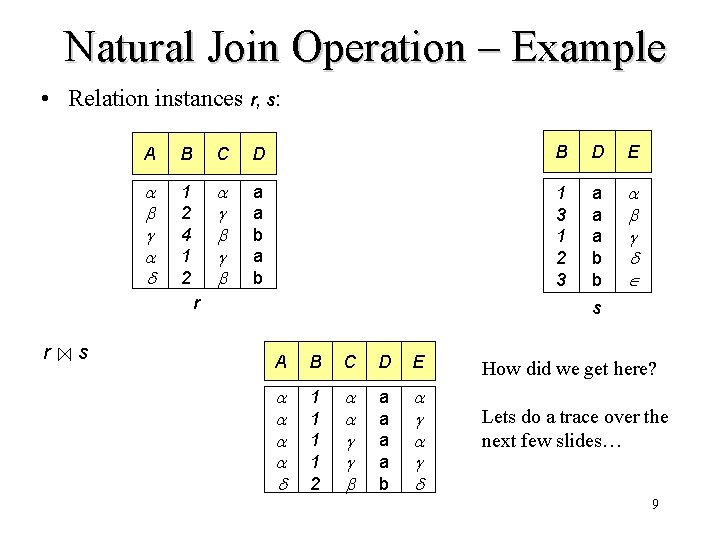
Natural Join Operation – Example • Relation instances r, s: A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r r s s A B C D E 1 1 2 a a b How did we get here? Lets do a trace over the next few slides… 9
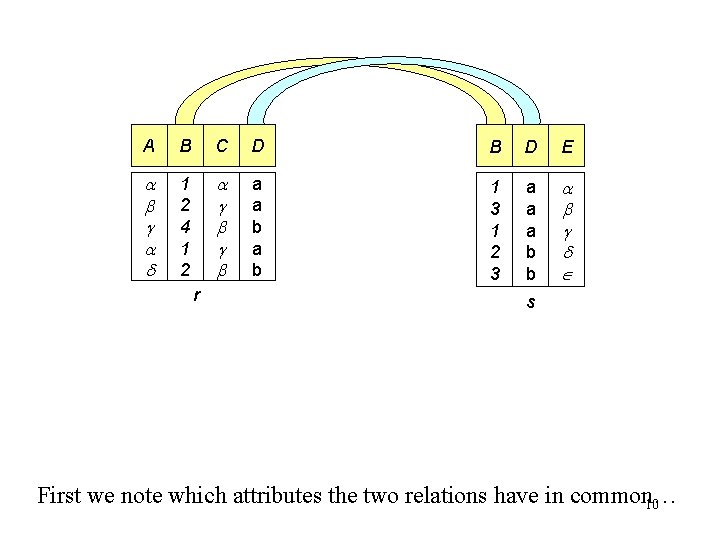
A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r s First we note which attributes the two relations have in common… 10
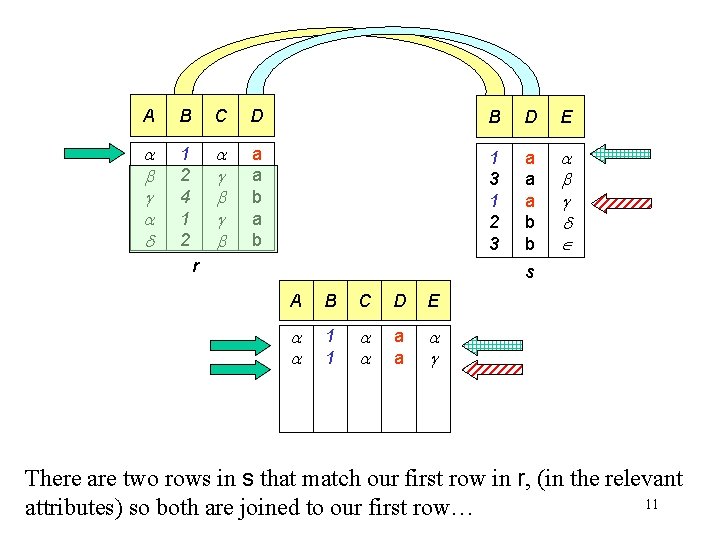
A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r s A B C D E 1 1 a a There are two rows in s that match our first row in r, (in the relevant 11 attributes) so both are joined to our first row…
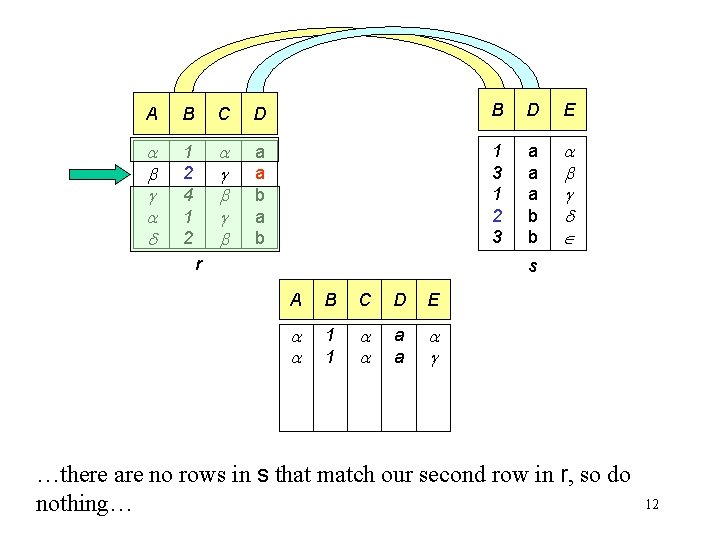
A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r s A B C D E 1 1 a a …there are no rows in s that match our second row in r, so do nothing… 12
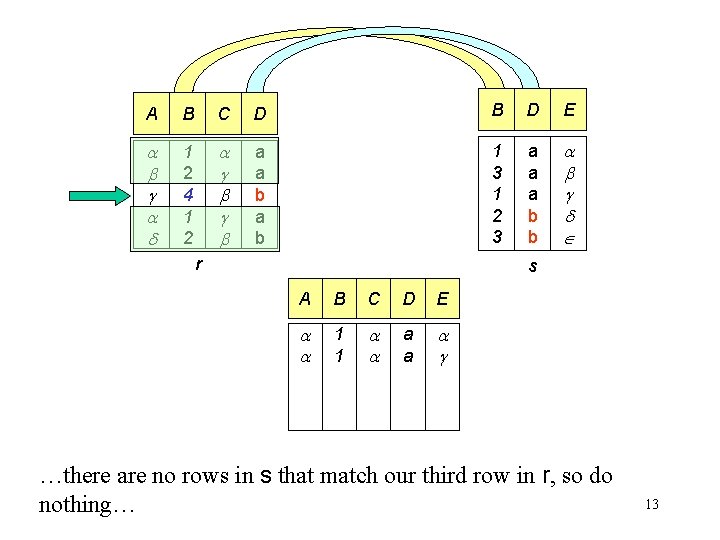
A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r s A B C D E 1 1 a a …there are no rows in s that match our third row in r, so do nothing… 13
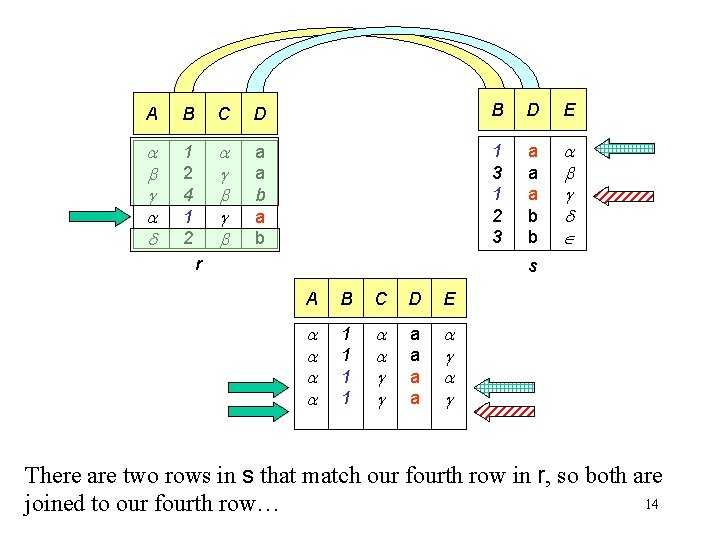
A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r s A B C D E 1 1 a a There are two rows in s that match our fourth row in r, so both are 14 joined to our fourth row…
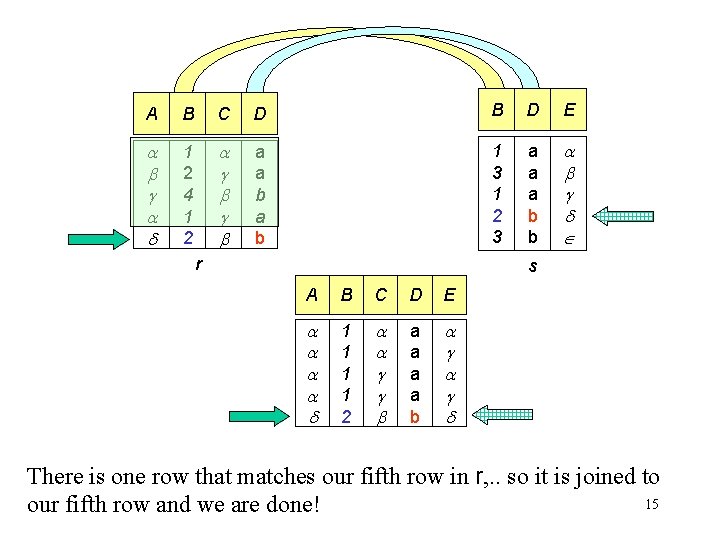
A B C D B D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b r s A B C D E 1 1 2 a a b There is one row that matches our fifth row in r, . . so it is joined to 15 our fifth row and we are done!
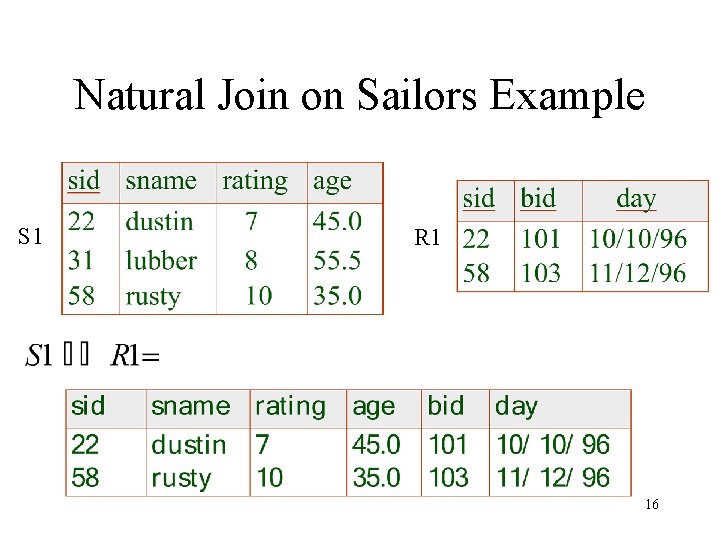
Natural Join on Sailors Example S 1 R 1 16

Last week we saw… Query: Find the name of the sailor who reserved boat 101. * Note my use of “temporary” relation Temp. 17

Query revisited using natural join Query: Find the name of the sailor who reserved boat 101. 18

Conditional-Join Operation: The conditional join is actually the most general type of join. We introduced the natural join first only because it is more intuitive and. . . natural! Just like natural join, conditional join combines a cross product and a selection into one operation. However instead of only selecting rows that have equality on those attributes that appear in both relation schemes, we allow selection based on any predicate. r c s = c(r x s) Where c is any predicate on the attributes of r and/or s Duplicate rows are removed as always, but duplicate columns are not removed! 19

Conditional-Join Example: We want to find all women that are younger than their husbands… r l-name f-name marr-Lic age l-name Simpson Marge 777 35 Simpson Homer Lovejoy Helen 234 38 Flanders Maude 555 24 Krabappel Edna 40 r 978 s Lovejoy f-name marr-Lic age 777 36 Timothy 234 36 Simpson Bart null r. age < s. age AND r. Marr-Lic = s. Marr-Lic 9 s r. l-name r. f-name r. Marr-Lic r. age s. l-name s. f-name s. marr-Lic s. age Simpson Marge 35 Homer 777 36 777 Simpson Note we have removed ambiguity of attribute names by using “dot” notation 20 Also note the redundant information in the marr-lic attributes

Equi-Join • Equi-Join: Special case of conditional join where the conditions consist only of equalities. • Natural Join: Special case of equi-join in which equalities are specified on ALL fields having the same names in both relations. 21
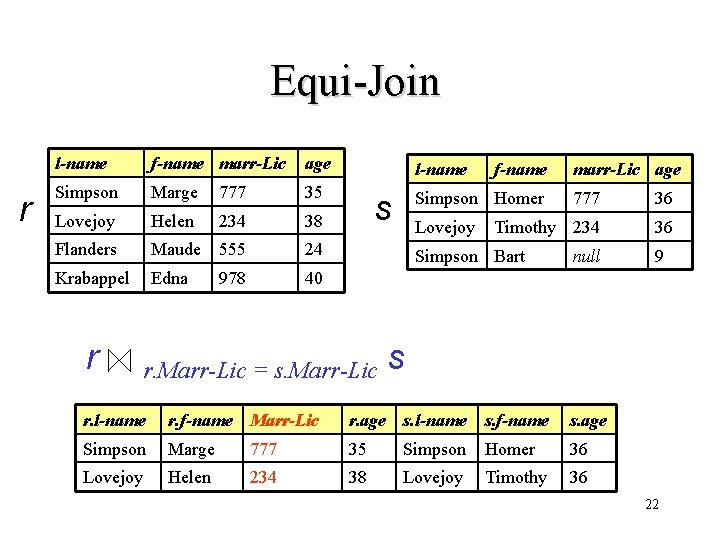
Equi-Join r l-name f-name marr-Lic age Simpson Marge 777 35 Lovejoy Helen 234 38 Flanders Maude 555 24 Krabappel Edna 40 r 978 l-name s f-name Simpson Homer Lovejoy 777 36 Timothy 234 36 Simpson Bart r. Marr-Lic = s. Marr-Lic marr-Lic age null 9 s r. l-name r. f-name Marr-Lic r. age s. l-name s. f-name s. age Simpson Marge 777 35 Simpson Homer 36 Lovejoy Helen 234 38 Lovejoy Timothy 36 22

Review on Joins • All joins combine a cross product and a selection into one operation. • Conditional Join – the selection condition can be of any predicate (e. g. rating 1 > rating 2) • Equi-Join: – Special case of conditional join where the conditions consist only of equalities. • Natural Join – Special case of equi-join in which equalities are specified on ALL fields having the same names in both relations. 23

Banking Examples branch (branch-name, branch-city, assets) customer (customer-name, customer-street, customer-only) account (account-number, branch-name, balance) loan (loan-number, branch-name, amount) depositor (customer-name, account-number) borrower (customer-name, loan-number) Note that I have not indicated primary keys here for simplicity. 24

Example Queries • Find all loans of over $1200 amount > 1200 (loan) loan amount > 1200 (loan) “select from the relation loan, only the rows which have an amount greater than 1200” loan-number 1234 3421 2342 4531 branch-name amount Riverside 1, 923. 03 Irvine 123. 00 Dublin 56. 25 Prague 120. 03 1234 Riverside 1, 923. 03 25

Example Queries • Find the loan number for each loan of an amount greater than $1200 loan-number ( amount > 1200 (loan)) “select from the relation loan, only the rows which have an amount greater than 1200, then project out just the loan_number” loan-number branch-name loan amount > 1200 (loan) loan-number ( amount > 1200 (loan)) amount 1234 Riverside 1, 923. 03 3421 Irvine 123. 00 2342 Dublin 56. 25 4531 Prague 120. 03 1234 Riverside 1, 923. 03 1234 26

Example Queries • Find all loans greater than $1200 or less than $75 amount > 1200 amount < 75(loan) “select from the relation loan, only the rows which have an amount greater than 1200 or an amount less than 75 loan-number branch-name loan amount > 1200 amount < 75(loan) amount 1234 Riverside 1, 923. 03 3421 Irvine 123. 00 2342 Dublin 56. 25 4531 Prague 120. 03 1234 Riverside 2342 Dublin 1, 923. 03 56. 25 27

Example Queries • Find the names of all customers who have a loan, an account, or both, from the bank customer-name (borrower) customer-name (depositor) borrower depositor customer-name loan-number customer-name account-number Patty 1234 Moe 3467 Apu 3421 Apu 2312 Selma 2342 Patty 9999 Ned 4531 Krusty 3423 customer-name (borrower) Moe Apu customer-name (depositor) Patty Moe Apu Krusty Apu Selma Patty Ned Krusty 28

Example Queries Note this example is split over two slides! Find the names of all customers who have a loan at the Riverside branch. customer-name ( branch-name=“Riverside ” ( borrower. loan-number = loan-number (borrower x loan))) borrower We retrieve borrower and loan… …we calculate their cross product… loan customer-name loan-number branch-name amount Patty 1234 Riverside 1, 923. 03 Apu 3421 Irvine customer-name borrower. loannumber branch-name Patty 1234 Riverside Patty 1234 3421 Irvine Apu 3421 1234 Riverside 1, 923. 03 Apu 3421 Irvine 29123. 00 amount 1, 923. 03 123. 00
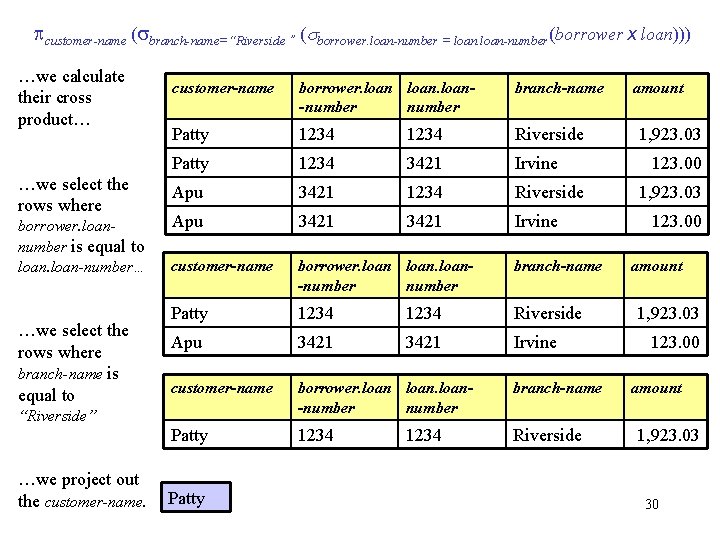
customer-name ( branch-name=“Riverside ” ( borrower. loan-number = loan-number(borrower x loan))) …we calculate their cross product… …we select the rows where borrower. loannumber is equal to loan-number… …we select the rows where branch-name is equal to customer-name borrower. loan-number branch-name Patty 1234 Riverside Patty 1234 3421 Irvine Apu 3421 1234 Riverside Apu 3421 Irvine customer-name borrower. loan-number branch-name Patty 1234 Riverside “Riverside” …we project out the customer-name. Patty 1234 amount 1, 923. 03 123. 00 amount 1, 923. 03 30

Now Using Natural Join Find the names of all customers who have a loan at the Riverside branch. customer-name ( branch-name=“Riverside ” ( borrower. loan-number = loan-number(borrower x loan))) => customer-name ( branch-name=“Riverside ” borrower We retrieve borrower and loan… 1234 in borrower is matched with 1234 in loan… 3421 in borrower is matched with 3421 in loan… The rest is the same. loan)) borrower loan customer-name loan-number branch-name amount Patty 1234 Riverside 1, 923. 03 Apu 3421 Irvine customer-name borrower. loan-number branch-name Patty 1234 Riverside 1234 123. 00 amount 1, 923. 03 123. 00 amount 31 1, 923. 03

Example Queries Note this example is split over three slides! Find the largest account balance. . . we will need to rename account relation as d. . . balance(account) - account. balance( account. balance < d. balance (account x r(d, account))) d account We do a rename to get a “copy” of account which we call d… … next we will do a cross product… account- balance number accountnumber Apu 100. 30 Patty 12. 34 Lenny 45. 34 balance 32
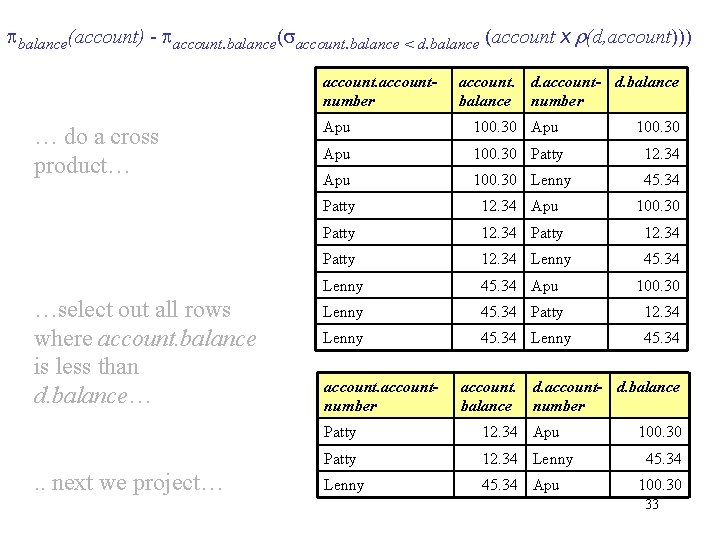
balance(account) - account. balance( account. balance < d. balance (account x r(d, account))) accountnumber … do a cross product… …select out all rows where account. balance is less than d. balance…. . next we project… account. d. account- d. balance number Apu 100. 30 Patty 12. 34 Apu 100. 30 Lenny 45. 34 Patty 12. 34 Apu 100. 30 Patty 12. 34 Lenny 45. 34 Apu 100. 30 Lenny 45. 34 Patty 12. 34 Lenny 45. 34 accountnumber account. d. account- d. balance number Patty 12. 34 Apu Patty 12. 34 Lenny 45. 34 Apu 100. 30 45. 34 100. 30 33
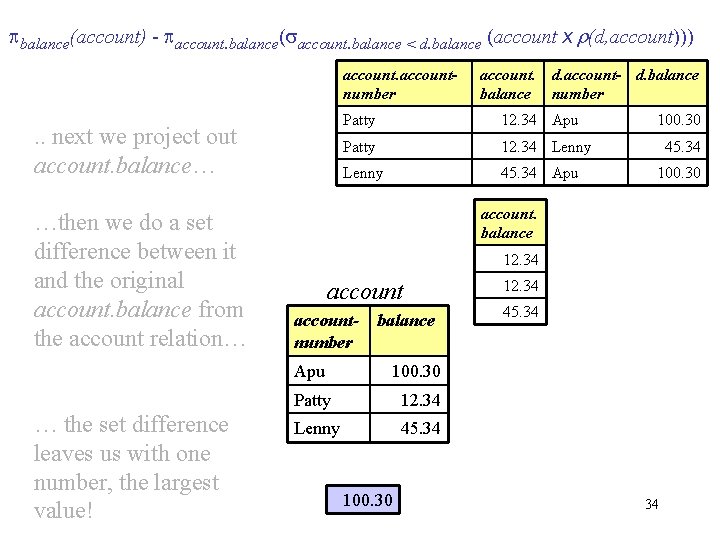
balance(account) - account. balance( account. balance < d. balance (account x r(d, account))) accountnumber . . next we project out account. balance… …then we do a set difference between it and the original account. balance from the account relation… … the set difference leaves us with one number, the largest value! account. d. account- d. balance number Patty 12. 34 Apu Patty 12. 34 Lenny 45. 34 Apu 100. 30 45. 34 100. 30 account. balance 12. 34 account- balance number Apu 100. 30 Patty 12. 34 Lenny 45. 34 100. 30 12. 34 45. 34 34

Now Using Conditional Join Find the largest account balance. . . we will need to rename account relation as d. . . balance(account) - account. balance( account. balance < d. balance (account x r(d, account))) r(d, account) balance(account) - account. balance(account. balance < d. balance d) 35

More Examples on Sailors Relations Sailors(sid, sname, rating, age) Boats(bid, bname, color) Reserves(sid, bid, day) 36

Find names of sailors who’ve reserved boat #103 • Solution 1: • Solution 2: • Solution 3: 37

Find names of sailors who’ve reserved a red boat • Information about boat color only available in Boats; so need an extra join: • A more efficient solution: * A query optimizer can find this given the first solution! 38

Find sailors who’ve reserved a red or a green boat • Can identify all red or green boats, then find sailors who’ve reserved one of these boats: v Can also define Tempboats using union! (How? ) v What happens if is replaced by in this query?

Find sailors who’ve reserved a red and a green boat • Previous approach won’t work! Must identify sailors who’ve reserved red boats, sailors who’ve reserved green boats, then find the intersection (note that sid is a key for Sailors):

Consider yet another query • Find the sailor(s) (sid) who reserved all the red boats. R 1 B

Start an attempt • who reserved what boat: v All the red boats:

r /s Division Operation • Suited to queries that include the phrase “for all”, e. g. Find sailors who have reserved all red boats. • Let S 1 have 2 fields, x and y; S 2 have only field y: – S 1/S 2 = – i. e. , S 1/S 2 contains all x tuples (sailors) such that for every y tuple (redboat) in S 2, there is an xy tuple in S 1 (i. e, x reserved y). • In general, x and y can be any lists of fields; y is the list of fields in S 2, and x y is the list of fields of S 1. • Let r and s be relations on schemas R and S respectively where – R = (A 1, …, Am, B 1, …, Bn) – S = (B 1, …, Bn) The result of r / s is a relation on schema R – S = (A 1, …, Am) 43
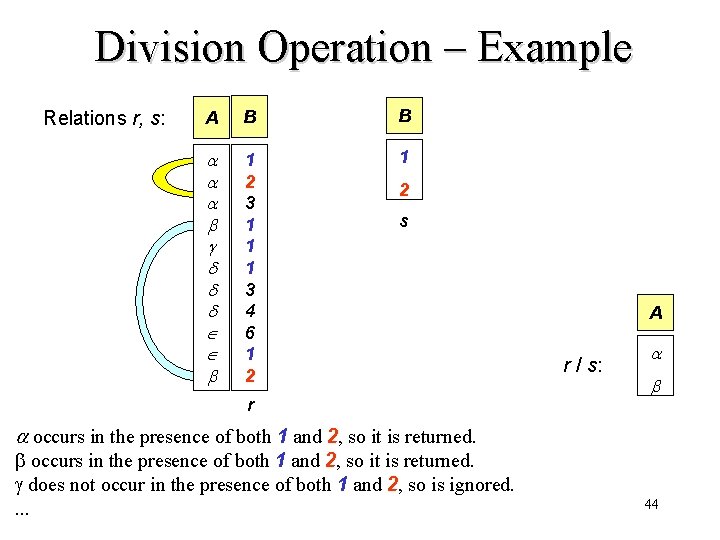
Division Operation – Example Relations r, s: A B B 1 2 3 1 1 1 3 4 6 1 2 s r A r / s: occurs in the presence of both 1 and 2, so it is returned. g does not occur in the presence of both 1 and 2, so is ignored. . 44
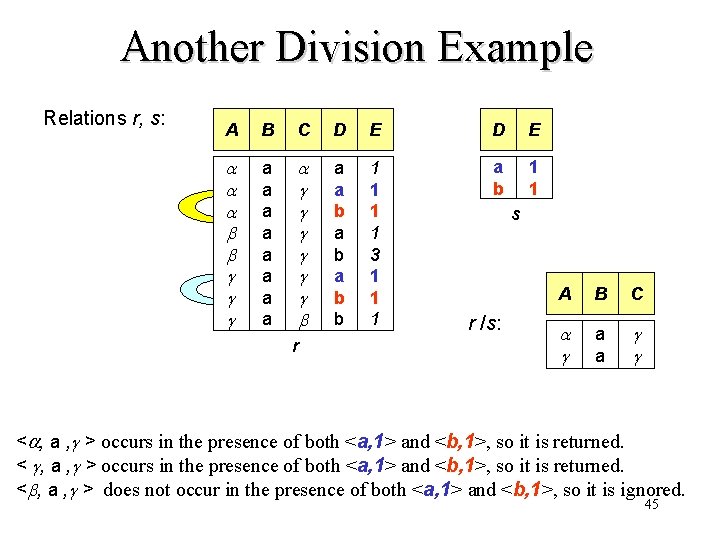
Another Division Example Relations r, s: A B C D E a a a a a a b a b b 1 1 3 1 1 1 a b 1 1 r s r /s: A B C a a < , a , > occurs in the presence of both <a, 1> and <b, 1>, so it is returned. < , a , > does not occur in the presence of both <a, 1> and <b, 1>, so it is ignored. 45
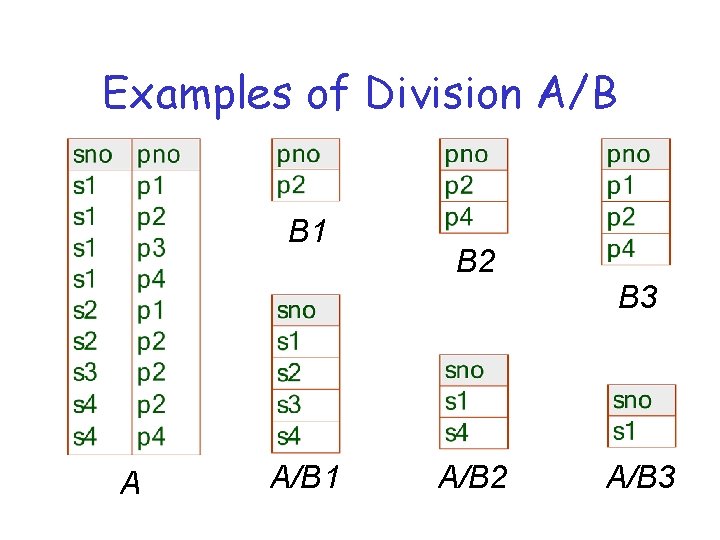
Examples of Division A/B B 1 B 2 B 3 A A/B 1 A/B 2 A/B 3

Find the sailor(s) who reserved ALL red boats • who reserved what boat: • All the red boats: => S 1/S 2 47

Find the names of sailors who’ve reserved all boats • Uses division; schemas of the input relations must be carefully chosen: v To find sailors who’ve reserved all ‘Interlake’ boats: . . .

Some Properties • Selection c 1Ù. . . Ù cn ( R) º c 1 (. . . cn ( R)) c 1 ( c 2 (R)) º c 2 ( c 1 (R)) • Projection l (R) º l 1 1 (. . . ( ln (R))) (Cascade) (Commute) (Cascade) where li is a subset of attributes in R, li li+1 • A projection commutes with a selection that only uses attributes retained by the projection: a 1, . . , an( c(a 1, . . , an) (R))= c(a 1, . . , an) ( a 1, . . , an( R )) where c(a 1, …, an) is a condition on attributes a 1, …, an

Properties of Joins • R c 1 • (R c. S) • c(R (S c S) c 2 T) (S (R (Associative) c 2 T (Commute) c. R) c(R) c 1 S) c S where c(a 1, …, an) is a condition on attributes only in R

Additional Operator: Outer Join • Joins: match tuples satisfying a join condition. – Tuples without a matching are discarded. – Tuples with Null value in at least one join attribute are discarded. • Outer Joins: useful when we want to keep tuples in one or both of the involved relations in a join operation that do not satisfy the join condition. – Left outer join – Right outer join – Full outer join • Schema of any Outer Join: Schema of Natural Join

Additional Operator: Outer Join • An extension of the join operation that avoids loss of information. • Computes the join and then adds tuples from one relation that does not match tuples in the other relation to the result of the join. • Uses null values: – null signifies that the value is unknown or does not exist – All comparisons involving null are (roughly speaking) false by definition. • Will study precise meaning of comparisons with nulls later 52

Outer Join – Example • Relation loan n Relation borrower loan-number branch-name L-170 L-230 L-260 Springfield Shelbyville Dublin amount 3000 4000 1700 customer-name loan-number Simpson Wiggum Flanders L-170 L-230 L-155 53
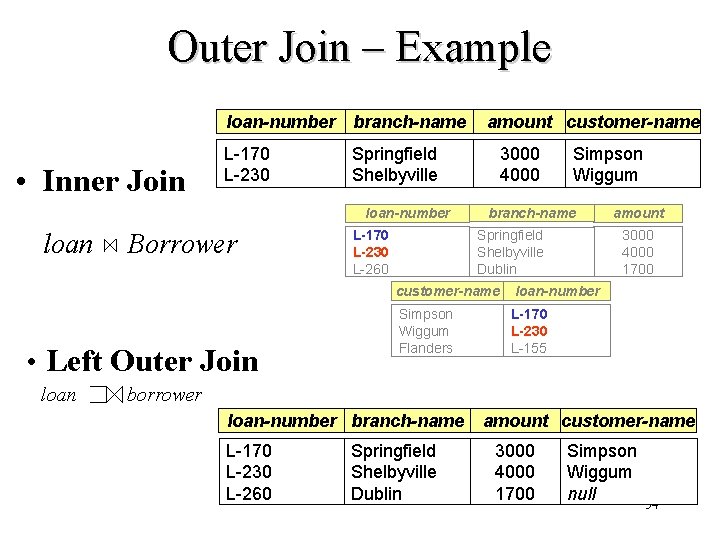
Outer Join – Example loan-number branch-name • Inner Join L-170 L-230 Springfield Shelbyville loan-number loan Borrower • Left Outer Join loan L-170 L-230 L-260 amount customer-name 3000 4000 Simpson Wiggum branch-name amount 3000 4000 1700 Springfield Shelbyville Dublin customer-name loan-number Simpson Wiggum Flanders L-170 L-230 L-155 borrower loan-number branch-name L-170 L-230 L-260 Springfield Shelbyville Dublin amount customer-name 3000 4000 1700 Simpson Wiggum null 54
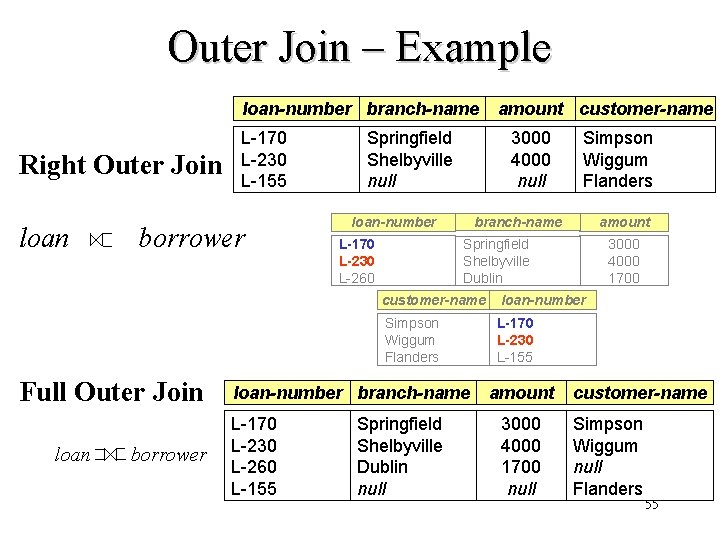
Outer Join – Example loan-number branch-name Right Outer Join loan borrower Full Outer Join loan L-170 L-230 L-155 borrower Springfield Shelbyville null 3000 4000 null loan-number L-170 L-230 L-260 Simpson Wiggum Flanders amount branch-name 3000 4000 1700 Springfield Shelbyville Dublin customer-name loan-number Simpson Wiggum Flanders L-170 L-230 L-155 loan-number branch-name L-170 L-230 L-260 L-155 amount customer-name Springfield Shelbyville Dublin null amount 3000 4000 1700 null customer-name Simpson Wiggum null Flanders 55

Full Outer Join • Full Outer Join. S R: keepseverytuplein both R and S, if not matching tuples are found in R (S), then the attributes in R (S) are set to Null (S R)

Cost of Relational Algebra Operations • Given two relations R, S, such as : Cardinality (R) = n, Cardinality(S) Cardinality = m • Cost O(n) c ( R ) a 1, …, an ( R ) • Cost O(n x m) Rx. S When working with Cross-product (Joins), keep input relations as small as possible!

Cost of Relational Algebra Operations Let q= max(m, n), Set Operations: R S, R – S: Cost O(q log q) Join Operations: R S, R Outer Joins Operations: R S, R c. S S, R S Best Case : attributes in the join condition include the primary key in S: Cost O(q log q) Otherwise : worst case : Cost O(m x n) When working with these operations, keep input relations as small as possible

Summary • The relational model has rigorously defined query languages that are simple and powerful. • Relational algebra is more operational; useful as internal representation for query evaluation plans. • Several ways of expressing a given query; a query optimizer should choose the most efficient version. • Operations covered: 5 basic operations (selection, projection, union, set difference, cross product), rename, joins (natural join, equi-join, conditional join, outer joins), division 59
- Slides: 59