Relational Algebra Database Management Systems Relational Algebra 1

Relational Algebra Database Management Systems

Relational Algebra- 1 Select, project, join
Query (expression) on set of relations produces relation as a result

Simple college admissions database ▪ College(c. Name, state, enrollment) ▪ Student(s. ID, s. Name, GPA, size. HS) ▪ Apply(s. ID, c. Name, major, decisions)
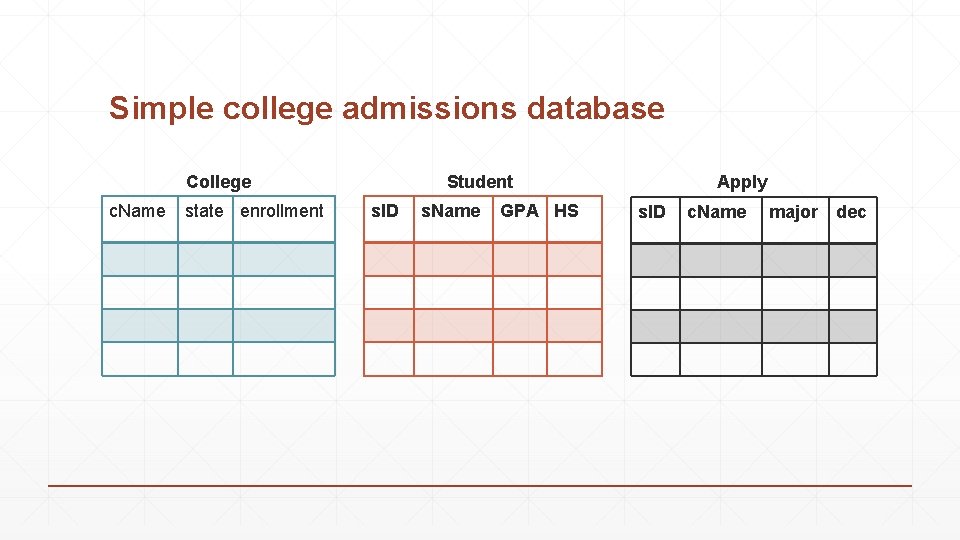
Simple college admissions database College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
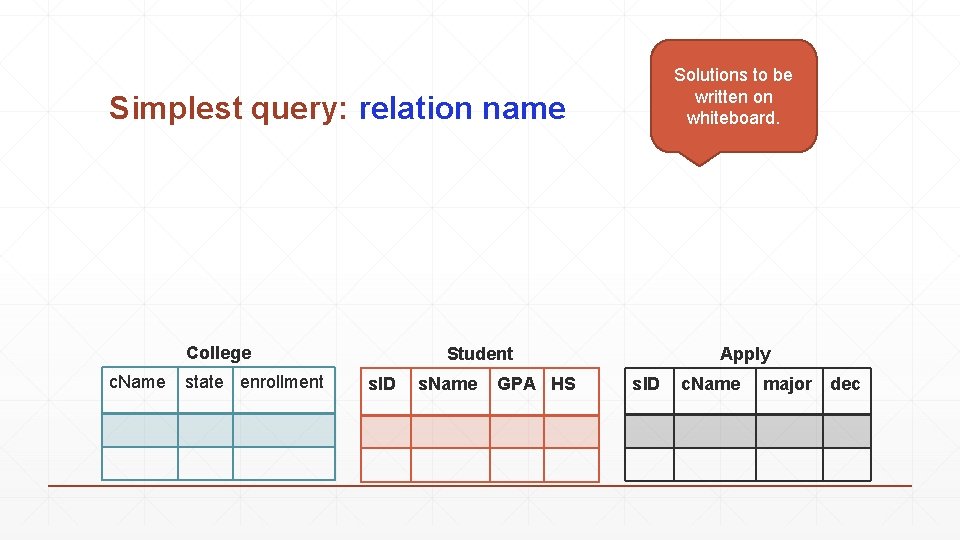
Solutions to be written on whiteboard. Simplest query: relation name College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
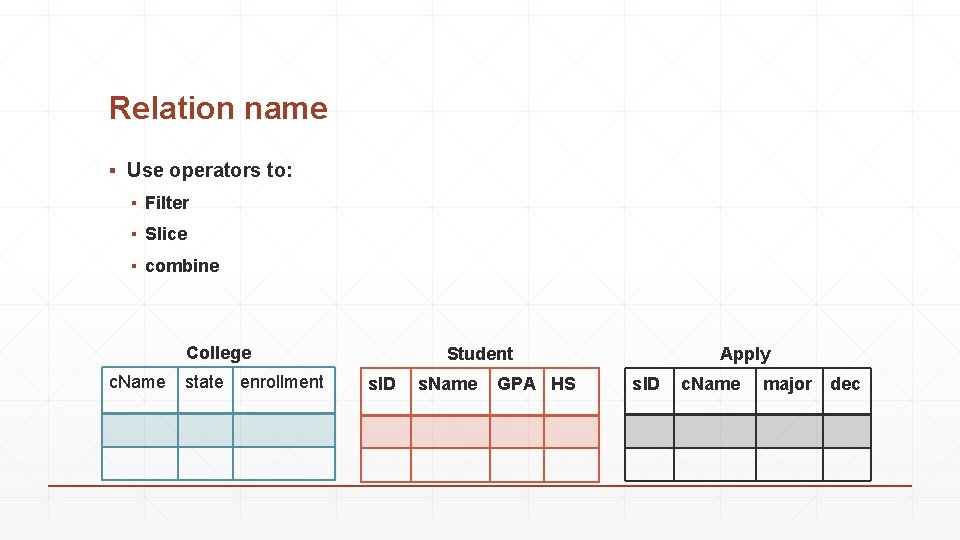
Relation name ▪ Use operators to: ▪ Filter ▪ Slice ▪ combine College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
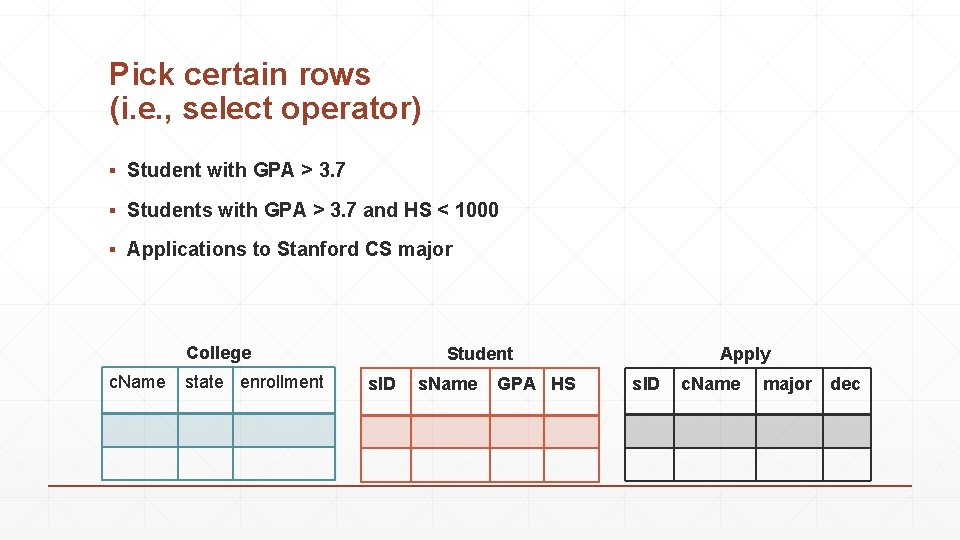
Pick certain rows (i. e. , select operator) ▪ Student with GPA > 3. 7 ▪ Students with GPA > 3. 7 and HS < 1000 ▪ Applications to Stanford CS major College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
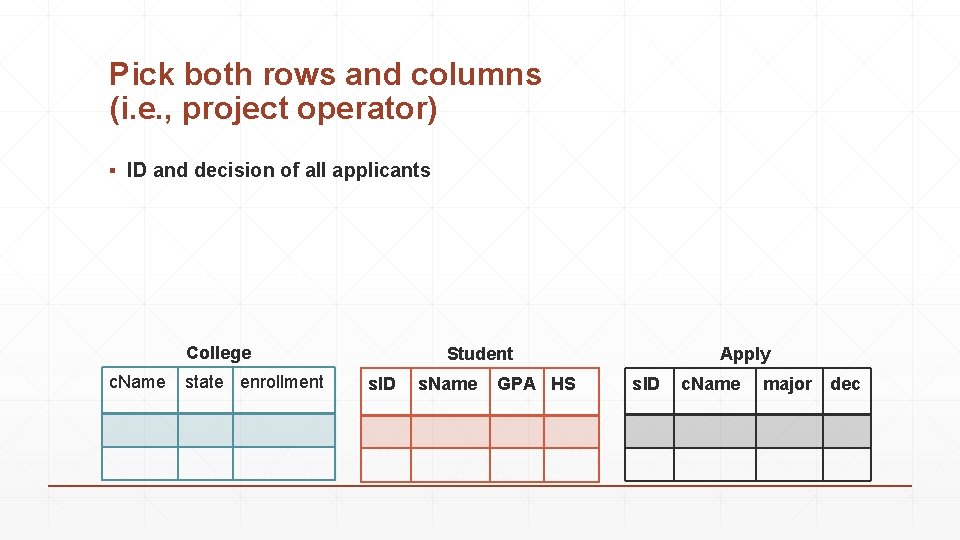
Pick both rows and columns (i. e. , project operator) ▪ ID and decision of all applicants College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
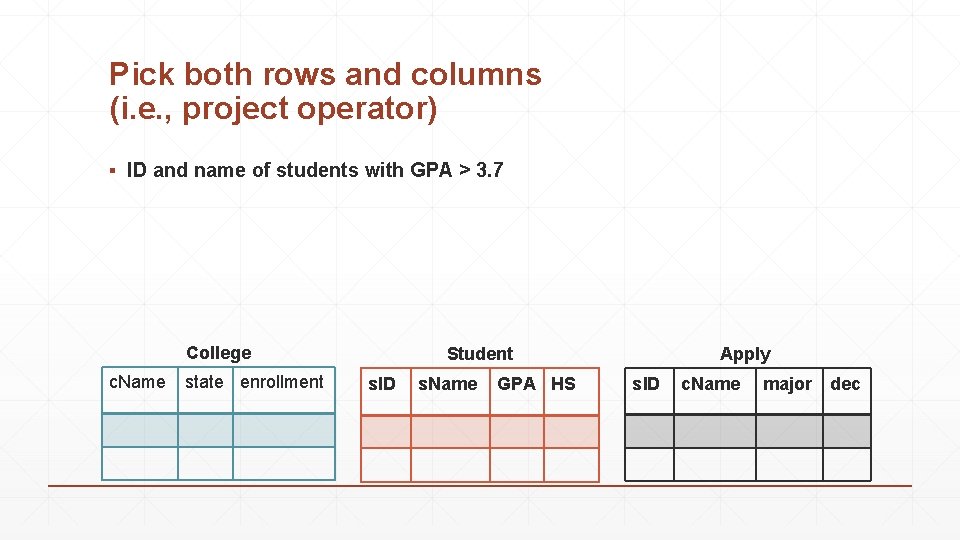
Pick both rows and columns (i. e. , project operator) ▪ ID and name of students with GPA > 3. 7 College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
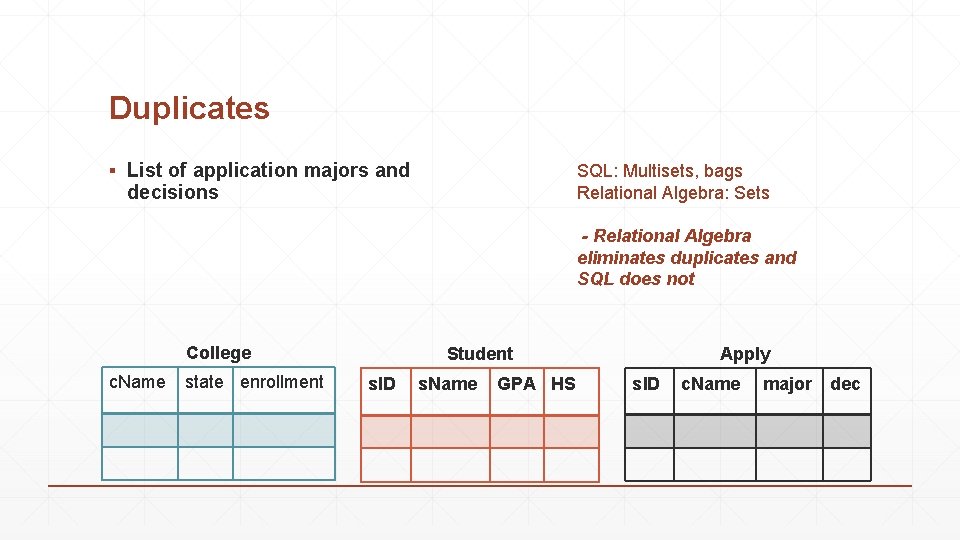
Duplicates ▪ List of application majors and decisions SQL: Multisets, bags Relational Algebra: Sets - Relational Algebra eliminates duplicates and SQL does not College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
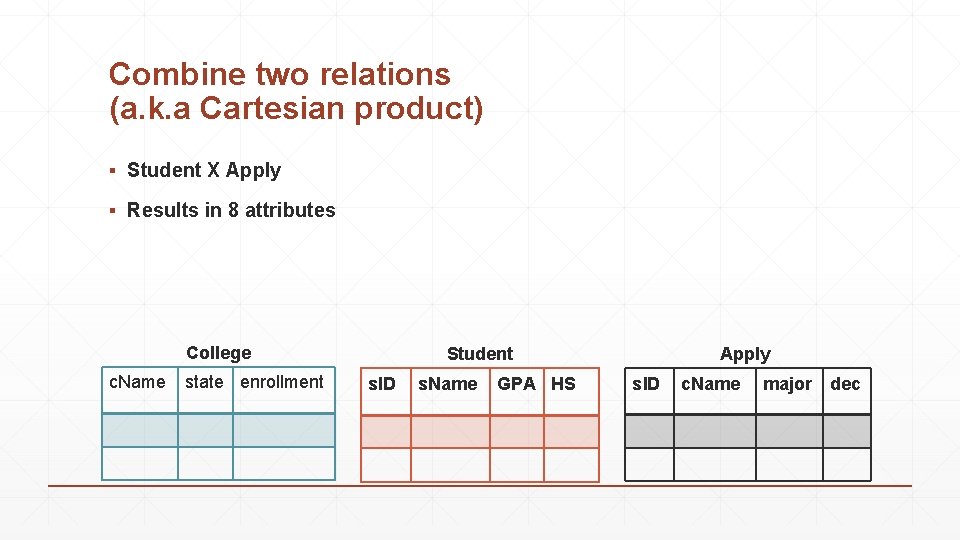
Combine two relations (a. k. a Cartesian product) ▪ Student X Apply ▪ Results in 8 attributes College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec

Combine two relations (a. k. a Cartesian product) ▪ Names and GPAs of students with HS > 1000 who applied to CS and were rejected ▪ (Student X Apply) College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec

Natural Join � ▪ Names and GPAs of students with HS > 1000 who applied to CS and were rejected ▪ (Student �Apply) ▪ It enforces equality on all attributes with the same name ▪ It eliminates one copy of duplicate attribute College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec

Natural Join � ▪ Names and GPAs of students with HS > 1000 who applied to CS at college with enr > 20, 000 and were rejected ▪ (Student �Apply) ▪ Technically, joins in Relational Algebra are Binary College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
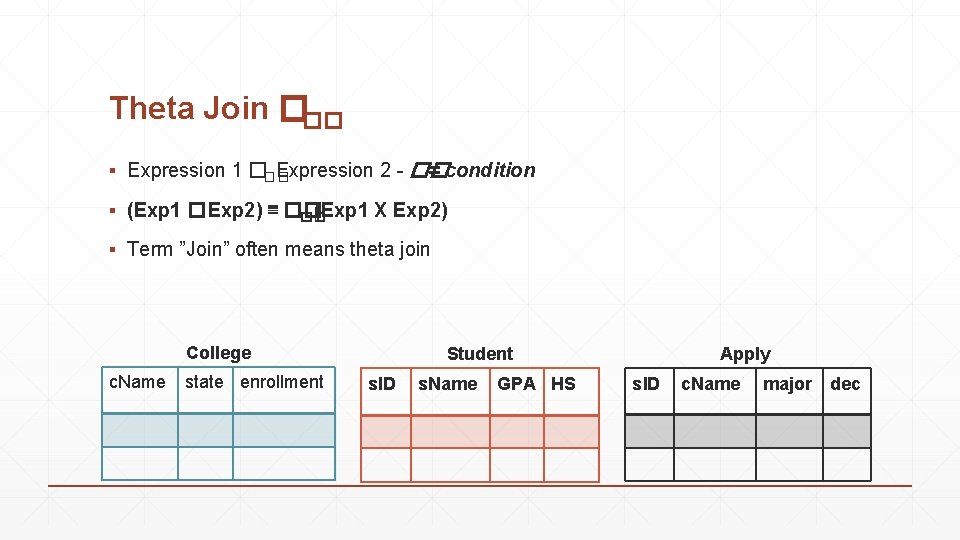
Theta Join ��� ▪ Expression 1 ��� Expression 2 - �� = condition ▪ (Exp 1 �Exp 2) ≣ �� (Exp 1 X Exp 2) �� ▪ Term ”Join” often means theta join College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec

Summary - 1 ▪ Query (expression) on set of relations produces relation as a result ▪ Simplest query: relation name ▪ Use operators to filer, slice, combine ▪ Operators so far: select, project, cross-product, natural join, theta join

Relational Algebra- 2 Set operators, renaming, notation

Union operator ▪ List of college and student names ▪ E. g. , Stanford, Susan, Cornell, Mary, Joh, Saint Joseph’s University, Mark ▪ c. Name College ∪ s. Name Student ▪ We only can union relations with the same attributes/schema ▪ We will take care of this later (Rename operator) College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
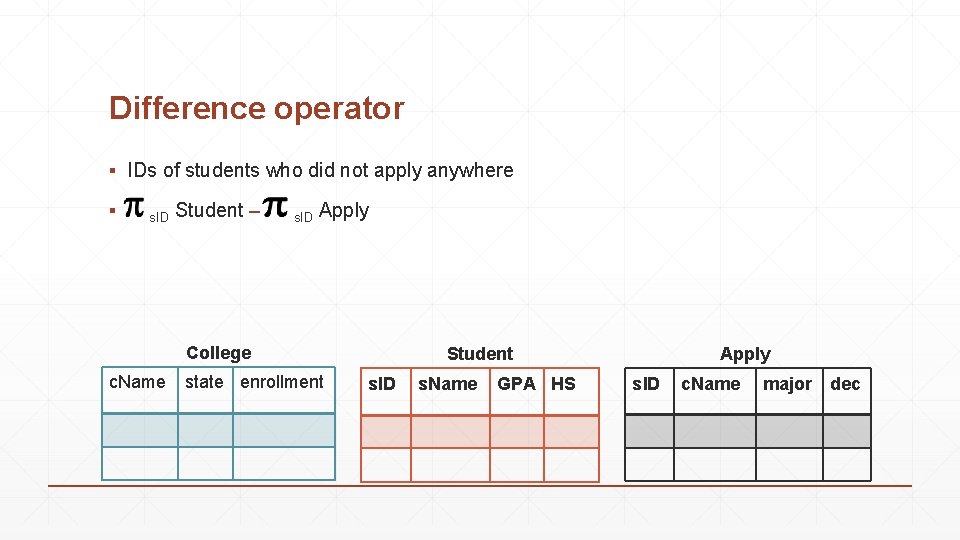
Difference operator ▪ IDs of students who did not apply anywhere ▪ s. ID Student – s. ID Apply College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
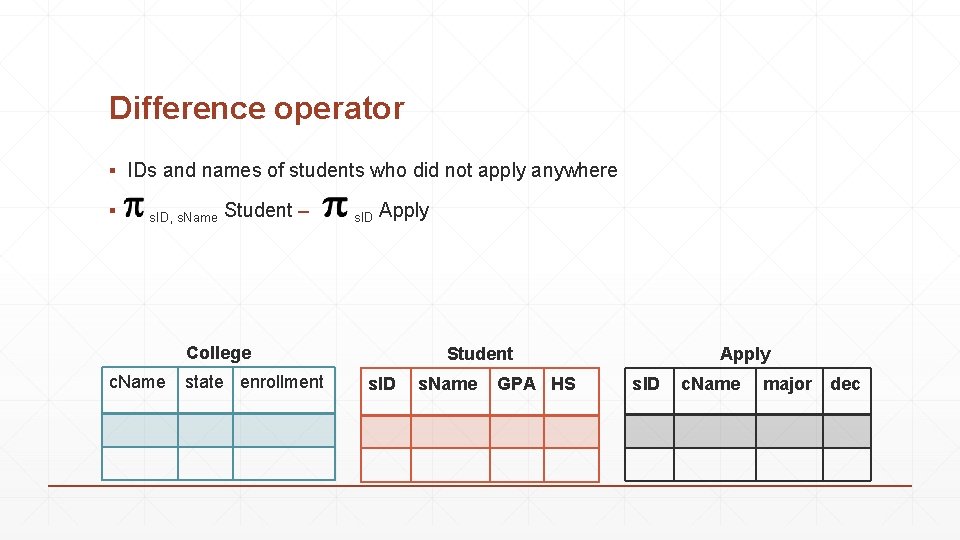
Difference operator ▪ IDs and names of students who did not apply anywhere ▪ s. ID, s. Name Student – s. ID Apply College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
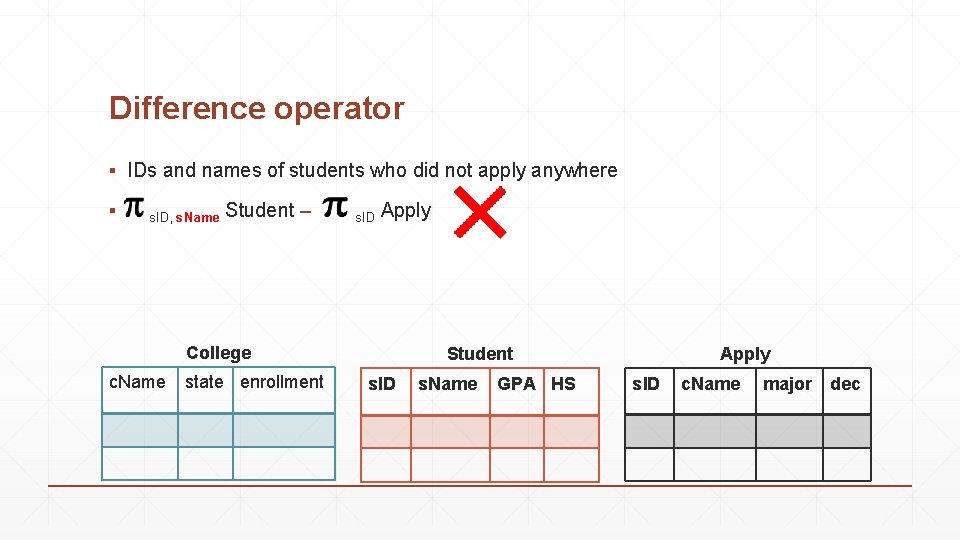
Difference operator ▪ IDs and names of students who did not apply anywhere ▪ s. ID, s. Name Student – s. ID Apply College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
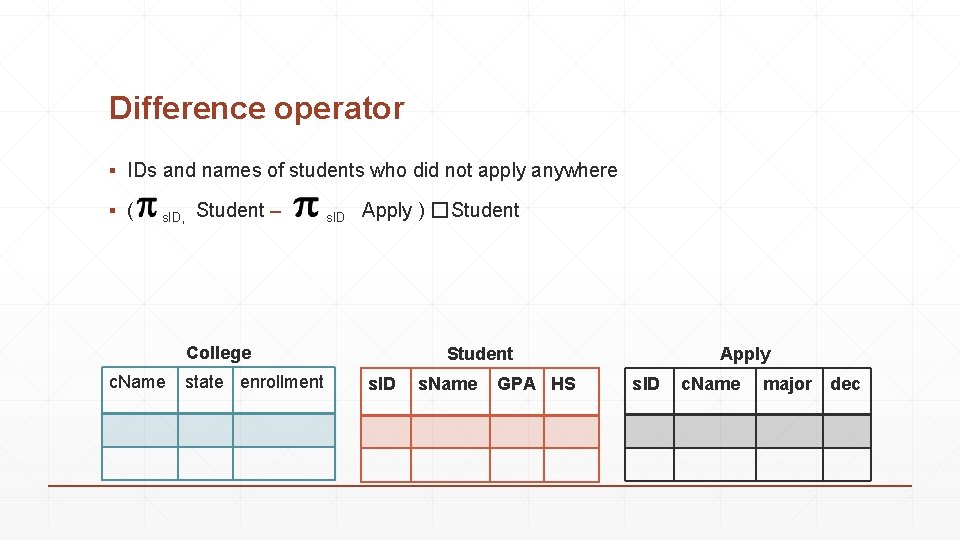
Difference operator ▪ IDs and names of students who did not apply anywhere ▪ ( s. ID, Student – s. ID Apply ) �Student College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
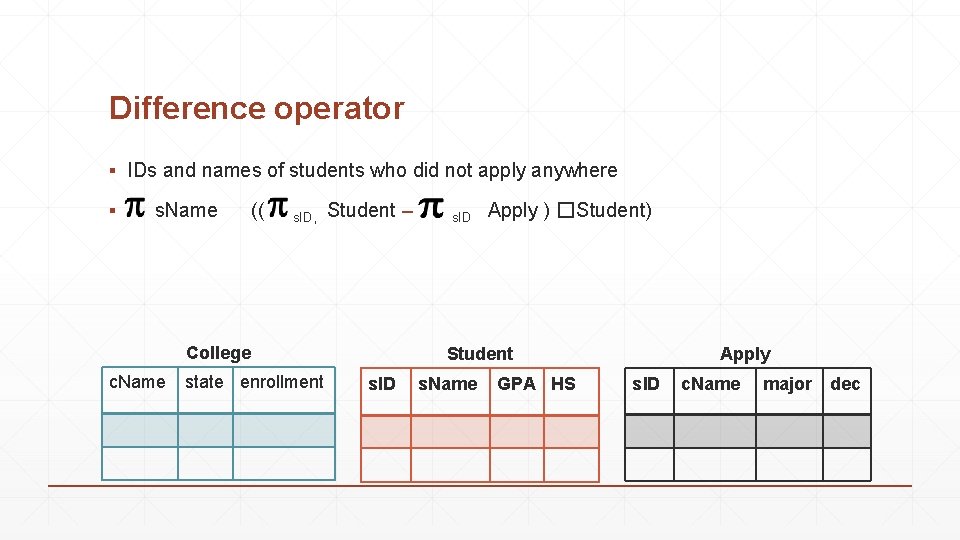
Difference operator ▪ IDs and names of students who did not apply anywhere ▪ s. Name (( s. ID, Student – College c. Name state enrollment s. ID Apply ) �Student) Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
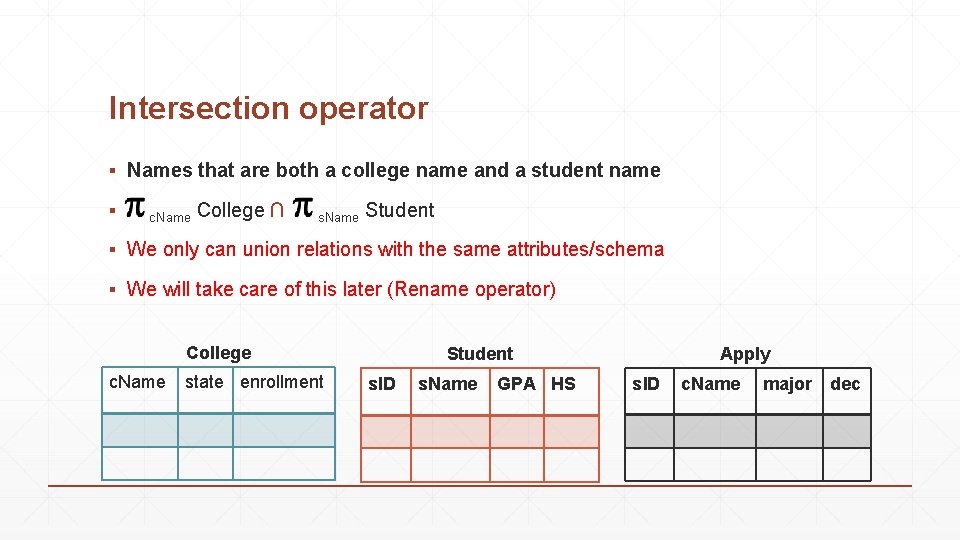
Intersection operator ▪ Names that are both a college name and a student name ▪ c. Name College ∩ s. Name Student ▪ We only can union relations with the same attributes/schema ▪ We will take care of this later (Rename operator) College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
Intersection operator ▪ Names that are both a college name and a student name ▪ c. Name College ∩ s. Name Student ▪ Intersection does not add expressive power ▪ E 1 ∩ E 2 ≣ E 1 �E 2 College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
Rename operator To unify schemas for set operators ▪ List of college and student names ▪ Rename attribute names such that it is possible to apply Union operator College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
Rename operator For disambiguation in ”self-join” ▪ Pairs of colleges in the same state College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
Alternate notation ▪ Assignment statements – pairs of colleges in same state College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
Alternate notation ▪ Expression tree – GPAs of students applying to CS in CA College c. Name state enrollment Student s. ID s. Name GPA HS Apply s. ID c. Name major dec
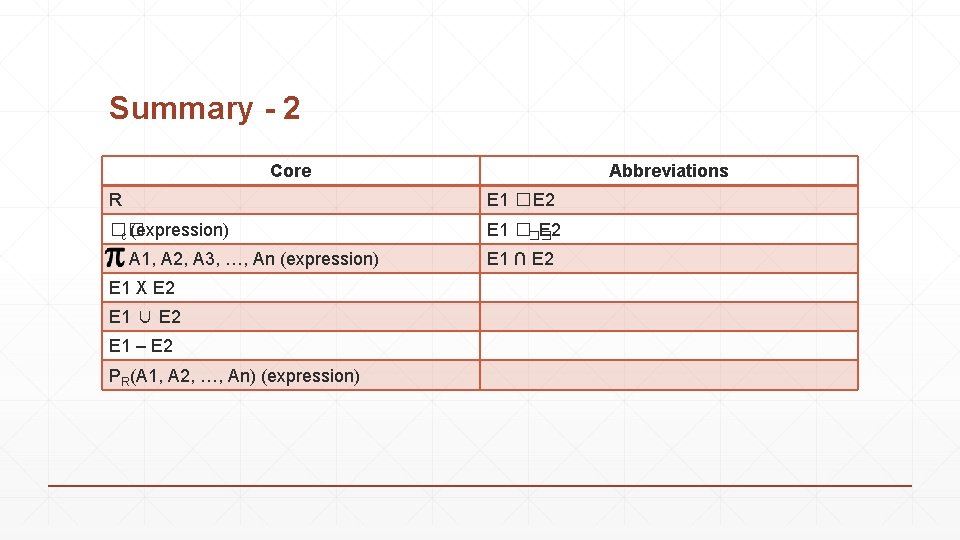
Summary - 2 Core Abbreviations R E 1 �E 2 �� c (expression) E 1 ��� E 2 A 1, A 2, A 3, …, An (expression) E 1 X E 2 E 1 ∪ E 2 E 1 – E 2 PR(A 1, A 2, …, An) (expression) E 1 ∩ E 2
- Slides: 31