RECURSION CITS 1001 2 Scope of this lecture

RECURSION CITS 1001

2 Scope of this lecture • Concept of recursion • Simple examples of recursion • Reading • The Blue. J book does not have a chapter on recursion • I recommend these notes from Princeton’s Intro to Programming course: • http: //introcs. princeton. edu/java/23 recursion/ • Some examples in these notes are sourced from here

3 Recursion • We have already seen that a method can call other methods • Either in the same class or in other classes • However a method can also call itself • This self-referential behaviour is known as recursion • We saw examples with Quicksort and Mergesort • Recursion is an extremely powerful technique for expressing certain complex programming tasks • It provides a very natural way to decompose problems • There are computational costs associated with recursion • The careful programmer will always be aware of these

4 The simplest example • The factorial of a positive integer k is the product of the integers between 1 and k k! = 1 × 2 × 3 × … × (k– 1) × k • In Java: private long factorial(long k) { long z = 1; for (long i = k; i > 1; i––) z *= i; return z; }

5 Think differently! k! = 1 × 2 × 3 × … × (k– 1) × k (k– 1)! = 1 × 2 × 3 × … × (k– 2) × (k– 1) k! = [1 × 2 × 3 × … × (k– 1)] × k k! = (k– 1)! × k • This is a recursive definition of factorial • Factorial defined in terms of itself • It uses factorial to define factorial

6 Something else is required 4! = 4 × 3 × 2! = 4 × 3 × 2 × 1 × 0! = 4 × 3 × 2 × 1 × 0 × (– 1)! … • We need something to tell it when to stop! • The base case of the recursion is when we know the result directly • 1! = 1

7 Recursive factorial in Java public static int factorial(int k) { if (k == 1) { return 1; } else { return k * factorial(k - 1); } } • In the base case • factorial stops and returns a result directly • In the recursive case • factorial calls itself with a smaller argument

8 What happens in the method call? factorial(4) =4* factorial(3) =3* factorial(2) factorial(1) factorial(0) factorial(2) =2* factorial(1) =1* =1 factorial(0)

9 Every k is a local variable • Each invocation of factorial has its own independent parameter k • factorial(4) creates a local variable k = 4 • Then factorial(3) creates its own local variable k = 3 • Then factorial(2) creates its own local variable k = 2 • Then factorial(1) creates its own local variable k = 1 • The compiler manages all of these variables for you, behind the scenes • Exactly as if you called any other method multiple times • Each invocation would have its own local variable(s)

10 Order is crucial • This will not work! private long factorial(long k) { return k * factorial(k – 1); if (k == 1) return 1; }

11 What could possibly go wrong? /** * factorial as above but with * exception handling for * the cases of <=0 input or * multiply overflow in the result */ public static int factorial. Robust(int k) { if (k <= 0) { throw new Illegal. Argument. Exception( "k must be >0 for factorial"); } if (k == 1) { return 1; } else { return Math. multiply. Exact( k, factorial. Robust(k - 1)); } }

12 Ingredients for a recursive definition • Every recursive definition must have two parts • One or more base cases • Each base case represents some “trivial case”, where we return a result directly • These are essential so that the recursion doesn’t go on forever • Often either a number being 0 or 1, or an array segment having length 0 or 1 • One or more recursive cases • The result is defined in terms of one or more calls to the same method, but with different parameters • The new parameters must be “closer to” the base case(s) in some sense • Often a number getting smaller, or an array segment getting shorter, or maybe two numbers getting closer together

13 Multiple base cases • Each Fibonacci number is the sum of the previous two Fibonacci numbers F 1 = 1 F 2 = 2 Fk = Fk– 1 + Fk– 2 1, 2, 3, 5, 8, 13, 21, …

14 Fibonacci in Java private long fib(long k) { if (k == 1) return 1; else if (k == 2) return 2; else return fib(k – 1) + fib(k – 2); } • This version is appalling slow, though • The number of calls to calculate fib(k) is Fk

15 Be careful though public int fibonacci(int n) { if (n == 0 || n == 1) { return 1; } else { return fibonacci(n-1)+ fibonacci(n-2); } This} looks fine, but in fact is disastrously slow because it unnecessarily repeats some calculations over and over again!

16 Faster Fibonacci private long fib 1(long k) { return fib 2(k, 1, 1); } private long fib 2(long k, long x, long y) { if (k == 1) return x; else return fib 2(k – 1, x + y, x); } • The number of calls to calculate fib 1(k) is k– 1 • Make sure you understand that fib 1(k) == fib(k)

17 Really fast Fibonacci private long fib 3(long k) { double sq 5 = Math. sqrt(5); double phi = (1 + sq 5) / 2; return Math. round(Math. pow(phi, k + 1) / sq 5); } • Constant time! • Make sure you understand that fib 3(k) == fib(k)

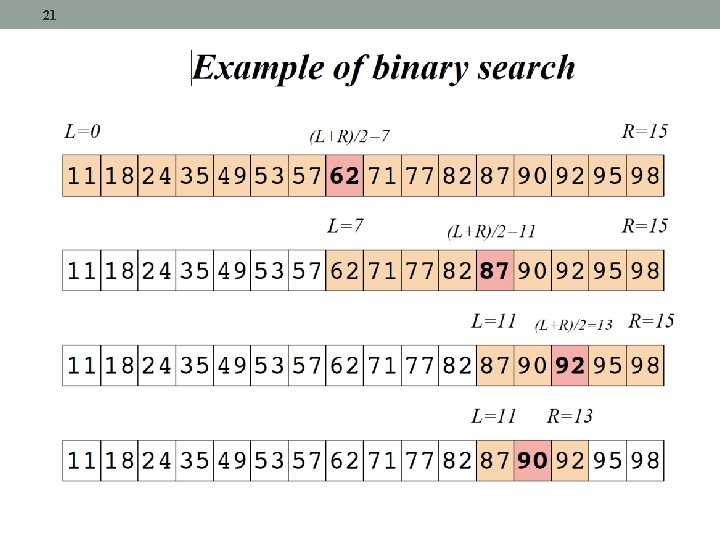
18 Binary search • We saw previously that linear search is very slow for large data • If the data is sorted, we can use the much faster binary search • Assume we are given an array of numbers in ascending order, and we want to check if the number z is in the array • Inspect the middle number • If the middle number is smaller than z, then if z is in the array, it must be in the top half • All numbers in the bottom half are smaller than z and can be ignored • If the middle number is larger than z, then if z is in the array, it must be in the bottom half

• Binary search can be expressed recursively in a very natural fashion, because we repeatedly perform the same operation of calculating the middle element and then searching in an array of half the size • What is the “simplest case” in this situation? • The length of the array is the parameter that is reduced at each stage of binary search and so the base case is when the left and the right bounds of the array are adjacent • In this situation it is trivial to determine whether or not the element we are looking for is in the array or not

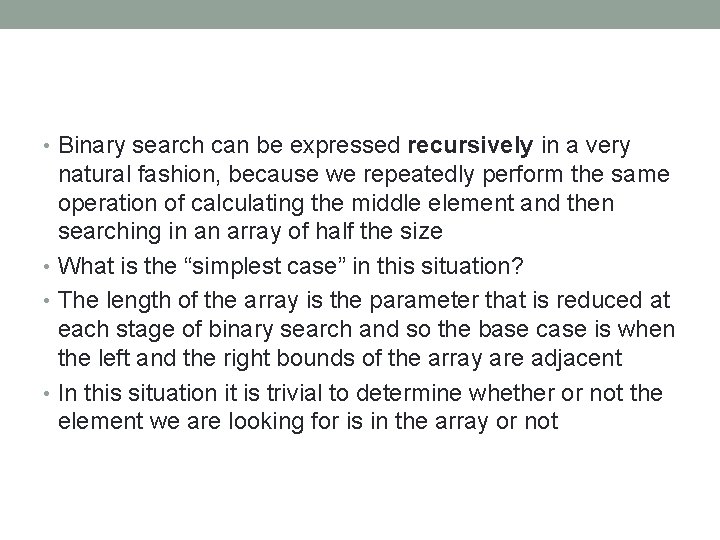
20 Code for binary search public static boolean binary. Search(int[] a, int z) { return bs(a, 0, a. length - 1, z); } // search a[l. . u] inclusive for z private static boolean bs(int[] a, int l, int u, int z) { if (l == u) return a[l] == z; else { int m = (l + u) / 2; if (a[m] < z) return bs(a, m + 1, u, z); else return bs(a, l, m, z); } }

21

22 Performance of binary search • Binary search is fast because: • In each recursive call, the size of the array that must be searched is reduced, in fact it is halved • So there will be log 2 n+1 calls, where n is the size of the original array • And also the base case is always reached because • In each recursive call, u–l defines the length of the array segment • u–l gets smaller in each call • When u–l hits 0, we use the base case

Practical considerations • If the array has 1024 entries, then Binary. Search will take at most 11 steps, as opposed to 1024 for the linear search • If the array has 10, 000 entries then the binary search will take at most 24 steps instead of 10, 000!! • Humans do an approximate binary search when using phone books, dictionaries and playing number guessing games

Recursive Graphics

Recursive Graphics • Simple recursive drawing schemes can lead to pictures that are remarkably intricate. • For example, an H-tree of order n is defined as follows: • The base case is null for n = 0. • The reduction step is to draw, within the unit square three lines in the shape of the letter H four H-trees of order n-1, one connected to each tip of the H with the additional provisos that the H-trees of order n-1 are centered in the four quadrants of the square, halved in size.

H-tree • Htree. java takes a command-line argument n, and plots to standard drawing an H-tree of order n. • An H-tree is a simple example of a fractal: a geometric shape that can be divided into parts, each of which is (approximately) a reduced size copy of the original.

draw(int n, double x, double y, double size) public static void draw(int n, double x, double y, double size) { if (n == 0) return; draw. H(x, y, size); // compute x- and y-coordinates of the 4 half-size H-trees double x 0 = x - size/2; double x 1 = x + size/2; double y 0 = y - size/2; double y 1 = y + size/2; // recursively draw 4 half-size H-trees of order n-1 draw(n-1, x 0, y 0, size/2); // lower left H-tree draw(n-1, x 0, y 1, size/2); // upper left H-tree draw(n-1, x 1, y 0, size/2); // lower right H-tree draw(n-1, x 1, y 1, size/2); // upper right H-tree }

draw. H(double x, double y, double size) public static void draw. H(double x, double y, double size) { // compute the coordinates of the 4 tips of the H double x 0 = x - size/2; double x 1 = x + size/2; double y 0 = y - size/2; double y 1 = y + size/2; // draw the 3 line segments of the H Std. Draw. line(x 0, y 0, x 0, y 1); // left vertical segment of the H Std. Draw. line(x 1, y 0, x 1, y 1); // right vertical segment of the H Std. Draw. line(x 0, y, x 1, y); // connect the two vertical segments of the H }

Objects First with Java - A Practical Introduction using Blue. J, © David J. Barnes, Michael Kölling The main method • Problem: How to execute Java without Blue. J • The answer: The java system always executes a method called main with a certain signature: public static void main(String[] args) {. . . } • For this to work, such a method must exist!

Objects First with Java - A Practical Introduction using Blue. J, © David J. Barnes, Michael Kölling The main method • main must exist. • main must be public. • main must be static (class method). • main must have a String[] parameter. • Only main can be invoked.

Objects First with Java - A Practical Introduction using Blue. J, © David J. Barnes, Michael Kölling Main method - example public static void main(String[] args) { Game game = new Game(); game. play(); } • Consider placing in a separate class, containing just this. • The main method should • create an object • call the first method

Htree main method // reads an integer command-line argument n // and plots an order n H-tree public static void main(String[] args) { int n = Integer. parse. Int(args[0]); double x = 0. 5, y = 0. 5; // center of H-tree double size = 0. 5; // side length of H-tree draw(n, x, y, size); }

Pitfalls of Recursion • With recursion, you can write compact and elegant programs that fail spectacularly at runtime. • Study the following examples to help you to avoid the pitfalls.

Missing base case This function is supposed to compute harmonic numbers, but is missing a base case: public static double harmonic(int n) { return harmonic(n-1) + 1. 0/n; } If you call this function, it will repeatedly call itself and never return. Your program will eventually crash with a Stack. Overflow exception

No guarantee of convergence Another common problem is to include within a recursive function a recursive call to solve a sub-problem that is not smaller than the original problem. public static double harmonic(int n) { if (n == 1) { return 1. 0; } return harmonic(n) + 1. 0/n; } This goes into an infinite recursive loop for any value of its argument (except 1).

Excessive Memory Requirements If a function calls itself recursively an excessive number of times before returning, the memory required by Java to keep track of the recursive calls may be prohibitive. public static double harmonic(int n) { if (n == 0) return 0. 0; return harmonic(n-1) + 1. 0/n; } This method correctly computes the nth harmonic number However, calling it with a huge value of n will lead to a Stack. Overflow. Error

Excessive Computation The temptation to write a simple recursive program to solve a problem must always be tempered by the understanding that a simple program might require exponential time (unnecessarily), due to excessive recomputation. // Warning: spectacularly inefficient. public static long fibonacci(int n) { if (n == 0) return 0; if (n == 1) return 1; return fibonacci(n-1) + fibonacci(n-2); }

Dynamic Programming • A general approach to implementing recursive programs. • Beyond the scope of cits 1001 but here is a taste: • The basic idea is to store the answer to each sub-problem and then use the stored answers to solve the original problem. Solving the sub-problem only once avoids exponential blow-up.

Challenge: Recursive trees Write a program that takes a parameter n and produces the recursive patterns above for n equal to 1, 2, 3, 4 and 8 For more challenges, see http: //introcs. princeton. edu/java/23 recursion/

Summary • Recursion can be used to express some complex computations in an elegant way • But there are overheads for using recursion that the programmer needs to be aware of