Recursion Recursion What is recursion When one function



















- Slides: 23

Recursion

Recursion What is recursion? When one function calls itself directly or indirectly. Gcd. Find largest integer d that evenly divides into p and q. base case reduction step, converges to base case public static int gcd(int p, int q) { if (q == 0) return p; else return gcd(q, p % q); } base case reduction step 2

3

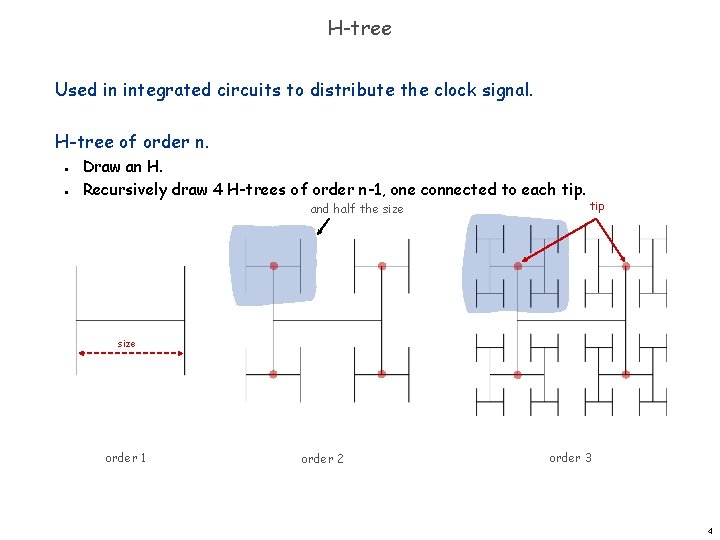
H-tree Used in integrated circuits to distribute the clock signal. H-tree of order n. n n Draw an H. Recursively draw 4 H-trees of order n-1, one connected to each tip. and half the size tip size order 1 order 2 order 3 4

Htree in Java public class Htree { public static void draw(int n, double sz, double x, double y) { if (n == 0) return; double x 0 = x - sz/2, x 1 = x + sz/2; double y 0 = y - sz/2, y 1 = y + sz/2; Std. Draw. line(x 0, y, x 1, y); Std. Draw. line(x 0, y 0, x 0, y 1); Std. Draw. line(x 1, y 0, x 1, y 1); draw the H, centered on (x, y) draw(n-1, recursively draw 4 half-size Hs sz/2, x 0, x 1, y 0); y 1); } public static void main(String[] args) { int n = Integer. parse. Int(args[0]); draw(n, . 5, . 5); } } 5

Computational Cost of the H-Tree Program H-tree of Order 1 • n 5 calls to draw() = 41 + 40 H-tree of Order 2 • n 21 calls to draw() = 42 + 41 + 40 H-tree of Order 3 • n F 85 calls to draw() = 43 + 42 + 41 + 40 Execution time grows exponentially 6

Towers of Hanoi http: //en. wikipedia. org/wiki/Image: Hanoiklein. jpg 7

Towers of Hanoi Move all the discs from the leftmost peg to the rightmost one. Only one disc may be moved at a time. A disc can be placed either on empty peg or on top of a larger disc. n n start finish Towers of Hanoi demo Edouard Lucas (1883) 8

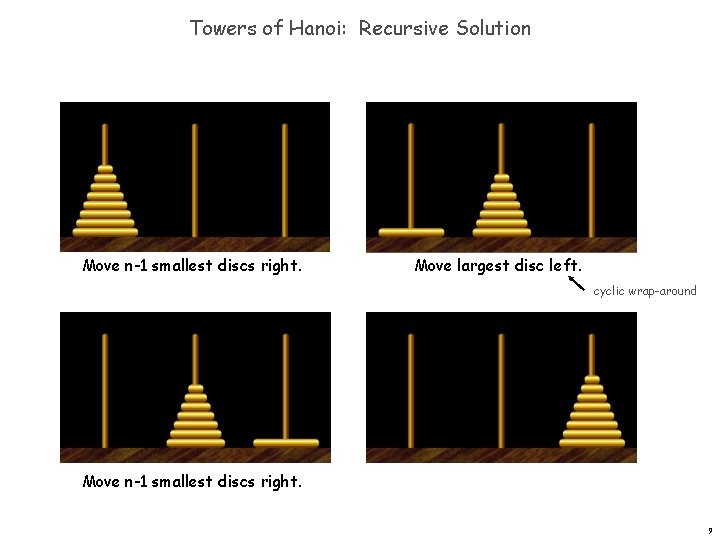
Towers of Hanoi: Recursive Solution Move n-1 smallest discs right. Move largest disc left. cyclic wrap-around Move n-1 smallest discs right. 9

Implementing the Recursive Solution Discs 1…n: • n 1 is the smallest disc, n is the largest moves(int n, boolean left): • n n moves(n, true): Moves discs 1…n one pole to the left moves(n, false): Move discs 1…n one pole to the right 10

Towers of Hanoi: Recursive Solution Dr. Java Demo public class Towers. Of. Hanoi { public static void moves(int n, boolean left) { if (n == 0) return; //base case moves(n-1, !left); //move n-1 discs to right if (left) System. out. println(n + " left"); else System. out. println(n + " right"); moves(n-1, !left); //move n-1 discs to right } public static void main(String[] args) { int N = Integer. parse. Int(args[0]); moves(N, true); } } moves(n, true) : move discs 1 to n one pole to the left moves(n, false): move discs 1 to n one pole to the right smallest disc 11

Recursive Function Call Tree On the Board 12

Computational Cost of Towers of Hanoi • T(n) = Number of moves required for moving n disks • T(1) = 1 • T(n) = 2*T(n-1) + 1 n Recurrence Relation 13

Computational Cost of Towers of Hanoi T(n) = 2*T(n-1)+1; T(1) = 1 • 2 Discs; T(2) = 3 moves • 3 Discs; T(3) = 7 moves • 4 Discs; T(4) = 15 moves • What is a closed-form expression for n discs? n F n Discs: T(n) = 2 n -1 Execution time grows exponentially 14

So What if Time Grows Exponentially? Assume that it takes 1 second to make a single move: • n n • • 1 disc: 21 -1 = 1 second 10 discs: 210 -1 seconds ~ 17 minutes 20 discs: 220 -1 seconds ~ 12 days 30 discs: 230 -1 seconds ~ 34 years! Algorithms with exponential running times are no match even for the fastest computers for large values of n Can we implement a non-recursive solution? 15

Outputs of the Recursive Solution % 1 2 1 3 1 2 1 java Towers. Of. Hanoi 3 left right left every other move is smallest disc % 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 java Towers. Of. Hanoi 4 right left right right left right Need to make a total of 2 n -1 moves 16

Divide-and-Conquer Divide-and-conquer paradigm. Break up problem into smaller subproblems of same structure. Solve subproblems recursively using same method. Combine results to produce solution to original problem. n n n Divide et impera. Veni, vidi, vici. - Julius Caesar Many important problems succumb to divide-and-conquer. n n n n FFT for signal processing. Parsers for programming languages. Multigrid methods for solving PDEs. Quicksort and mergesort for sorting. Hilbert curve for domain decomposition. Quad-tree for efficient N-body simulation. Midpoint displacement method for fractional Brownian motion. 17

Summary How to write simple recursive programs? Base case, reduction step. Trace the execution of a recursive program. Use pictures. n n n Why learn recursion? New mode of thinking. Powerful programming tool. n n Divide-and-conquer. Elegant solution to many important problems. 18

Homework 4 19

Eureka! 20

21

22

Two approaches 1. Random (“generate-and-test”) 2. Recursive 23
 One to one vs onto
One to one vs onto To understand recursion you must understand recursion
To understand recursion you must understand recursion One empire one god one emperor
One empire one god one emperor One one one little puppy run
One one one little puppy run One king one law one faith
One king one law one faith One god one empire one emperor
One god one empire one emperor One ford
One ford See one do one teach one
See one do one teach one One price policy
One price policy Twelfth night speeches
Twelfth night speeches Studiendekanat uni bonn
Studiendekanat uni bonn Asean tourism strategic plan
Asean tourism strategic plan One vision one identity one community
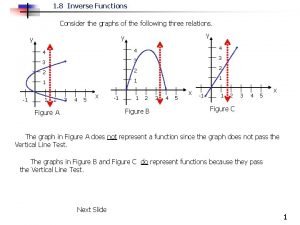
One vision one identity one community One to one function graph
One to one function graph Through one man
Through one man Get out one direction
Get out one direction 40 tens is how many hundreds
40 tens is how many hundreds Othello act 1 scene 1 summary
Othello act 1 scene 1 summary One team one fight meaning
One team one fight meaning One goal one passion
One goal one passion One gene one polypeptide concept
One gene one polypeptide concept Maybe this one moment with this one person
Maybe this one moment with this one person One voice one look
One voice one look One futureworld
One futureworld