Random Walk on Graph t0 Random Walk Start

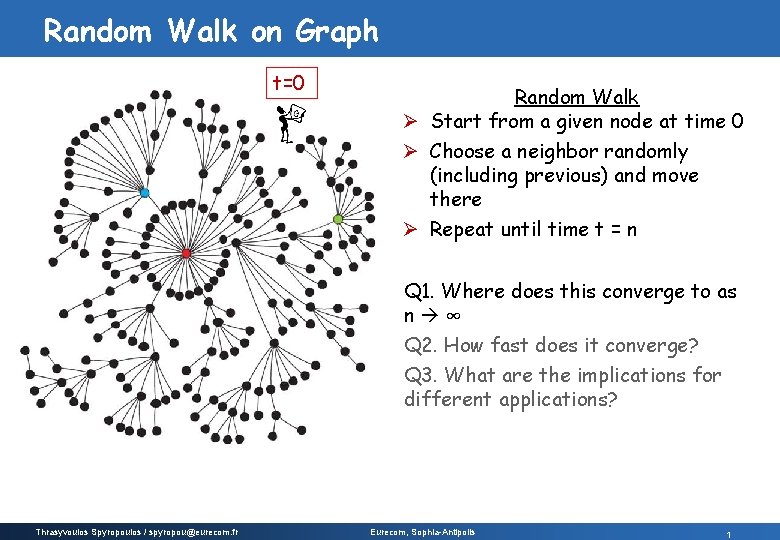
Random Walk on Graph t=0 Random Walk Ø Start from a given node at time 0 Ø Choose a neighbor randomly (including previous) and move there Ø Repeat until time t = n Q 1. Where does this converge to as n ∞ Q 2. How fast does it converge? Q 3. What are the implications for different applications? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 1

Random Walks on Graphs Ø Node degree ki move to any neighbor with prob = 1/ki 0 1 1 0 0 0 1 1 0 1/k 2 0 1 1 0 0 1 1 A= 1/k 1 0 0 1/k 2 0 1/k 3 0 0 1/k 3 1 0 1/k 4 0 0 0 1/k 5 0 Ø This is a Markov chain! Ø Start at a node i p(0) = (0, 0, …, 1, … 0, 0) Ø p(n) = p(0) An Ø π = π A [where π = limn ∞ p(n)] Q: what is π for a random walk on a graph? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 2

Random Walks on Undirected Graphs Ø Stationarity: π(z) = Σxπ(x)p(x, z) v p(x, y) = 1/kx Ø Could try to solve these or global balance. Not Easy!! Ø Define N(z): {neighbors of z) Σx ∈ N(z) kx⋅p(x, z) = Σx ∈ N(z) kx⋅(1/kx) = Σx ∈ N(z)1 = kz Ø Normalize by (dividing both sides with) Σxkx v Σxkx = 2|E| (|E| = m = # of edges) Σx ∈ N(z) (kx/2|E|)⋅p(x, z) = kz/2|E| Ø π(x) = kx/2|E| is the stationary distribution v always satisfies the stationarity eq π(x) = π(x)P Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 3

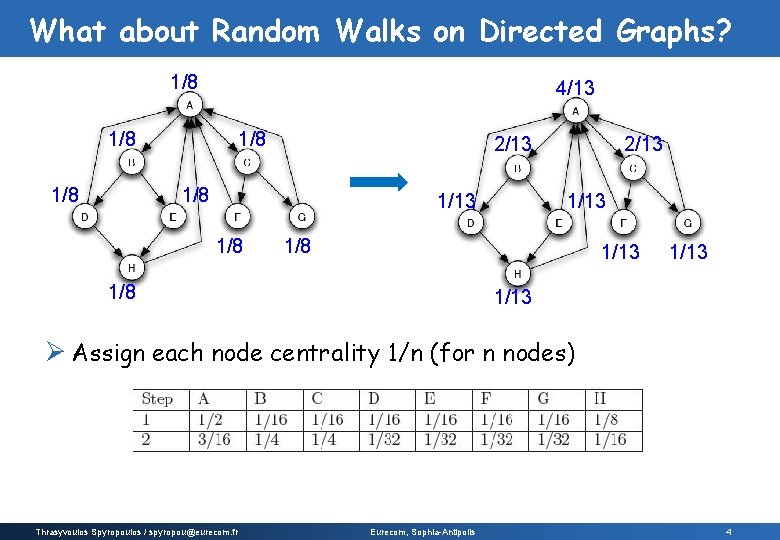
What about Random Walks on Directed Graphs? 1/8 4/13 1/8 1/8 2/13 1/8 1/13 1/13 Ø Assign each node centrality 1/n (for n nodes) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 4

A Problematic Graph Q: What is the problem with this graph? A: All centrality “points” will eventually go to F and G Solution: when at node i 1) 2) With probability β jump to any (of the total N) node(s) With 1 -β jump to a random neighbor of i Q: Does this remind you of something? A: Page. Rank algorithm! Page. Rank of node i is the stationary probability for a random walk on this (modified) directed graph v factor β in Page. Rank function avoids this problem by “leaking” some small amount of centrality from each node to all other nodes Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 5

Page. Rank Centrality Page. Rank as a Random Walk Ø A (bored) web surfer Ø Either surf a linked webpage with probability 1 -β Ø Or surf a random page (e. g. new search) with probability β Ø The probability of ending up at page X, after a large enough time = Page. Rank of page X! Ø Can generalize Page. Rank with general β = (β 1, β 2, …, βn) Ø Undirected network: removing β degree centrality Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 6

Applications of RW: Measuring Large Networks Ø We are interested in studying the properties (degree distribution, path lengths, clustering, connectivity, etc. ) of many real networks (Internet, Facebook, You. Tube, Flickr, etc. ) as this contain many important ($$$) information Ø E. g. to plot degree distribution, we need to crawl the whole network and obtain a “degree value” for each node. Ø This networks might contain millions of nodes!! Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 7

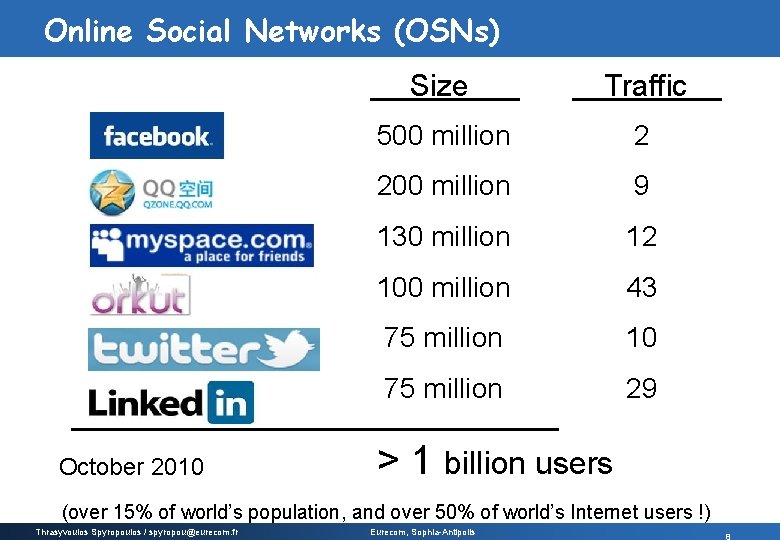
Online Social Networks (OSNs) October 2010 Size Traffic 500 million 2 200 million 9 130 million 12 100 million 43 75 million 10 75 million 29 > 1 billion users (over 15% of world’s population, and over 50% of world’s Internet users !) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

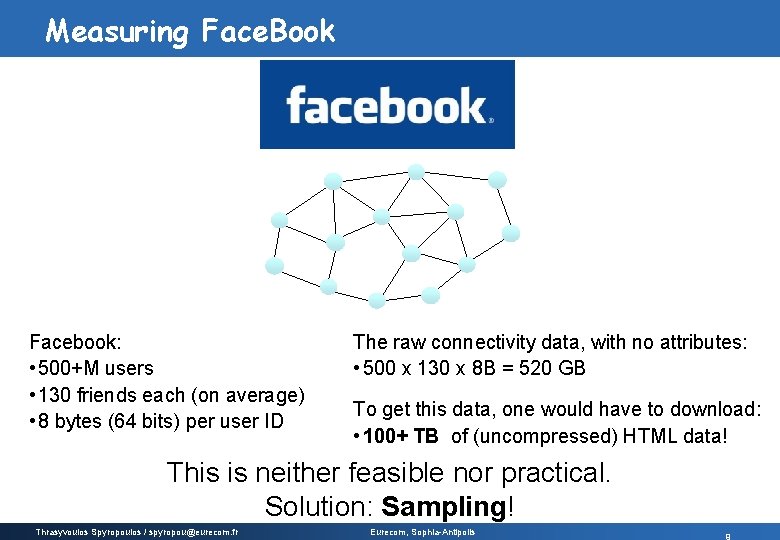
Measuring Face. Book Facebook: • 500+M users • 130 friends each (on average) • 8 bytes (64 bits) per user ID The raw connectivity data, with no attributes: • 500 x 130 x 8 B = 520 GB To get this data, one would have to download: • 100+ TB of (uncompressed) HTML data! This is neither feasible nor practical. Solution: Sampling! Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Measuring Large Networks (for the mere mortals) ØObtaining complete dataset difficult companies usually unwilling to share data v for privacy and performance reasons (e. g. Facebook will ban accounts if it sees extensive crawling) v tremendous overhead to measure all (~100 TB for Facebook) v ØRepresentative samples desirable study properties v test algorithms v Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Sampling What: • Topology? • Nodes? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr How: • Directly? • Exploration? Eurecom, Sophia-Antipolis

(1) Breadth-First-Search (BFS) Ø Starting from a seed, explores all neighbor nodes. Process continues iteratively without replacement. Ø BFS leads to bias towards high degree nodes v Lee et al, “Statistical properties of Sampled Networks”, Phys Review E, 2006 Ø Early measurement studies of OSNs use BFS as primary sampling technique v i. e [Mislove et al], [Ahn et al], [Wilson et al. ] Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

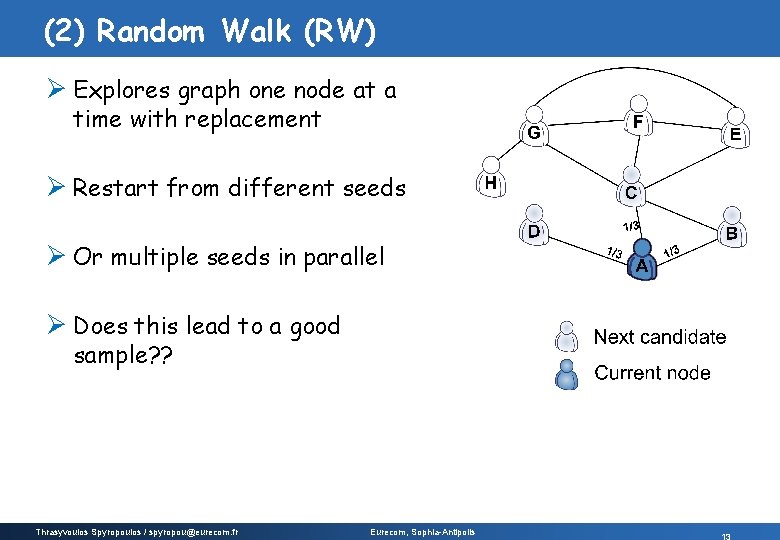
(2) Random Walk (RW) Ø Explores graph one node at a time with replacement Ø Restart from different seeds Ø Or multiple seeds in parallel Ø Does this lead to a good sample? ? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

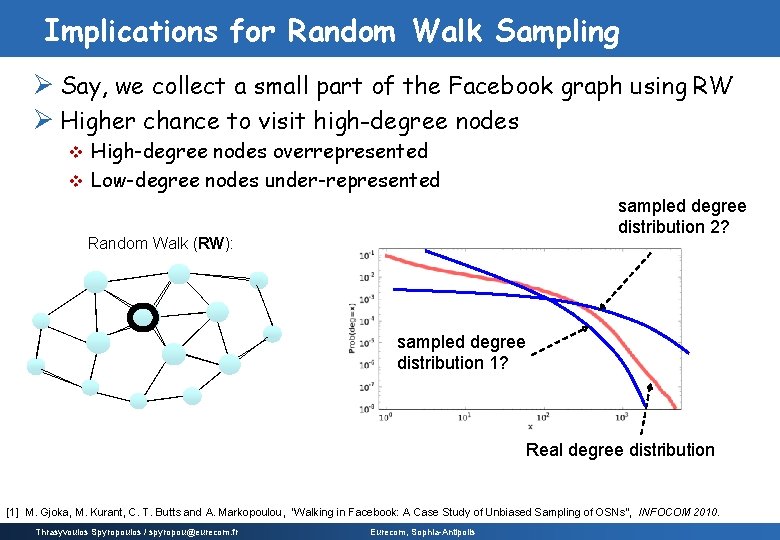
Implications for Random Walk Sampling Ø Say, we collect a small part of the Facebook graph using RW Ø Higher chance to visit high-degree nodes High-degree nodes overrepresented v Low-degree nodes under-represented v sampled degree distribution 2? Random Walk (RW): sampled degree distribution 1? Real degree distribution [1] M. Gjoka, M. Kurant, C. T. Butts and A. Markopoulou, “Walking in Facebook: A Case Study of Unbiased Sampling of OSNs”, INFOCOM 2010. Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

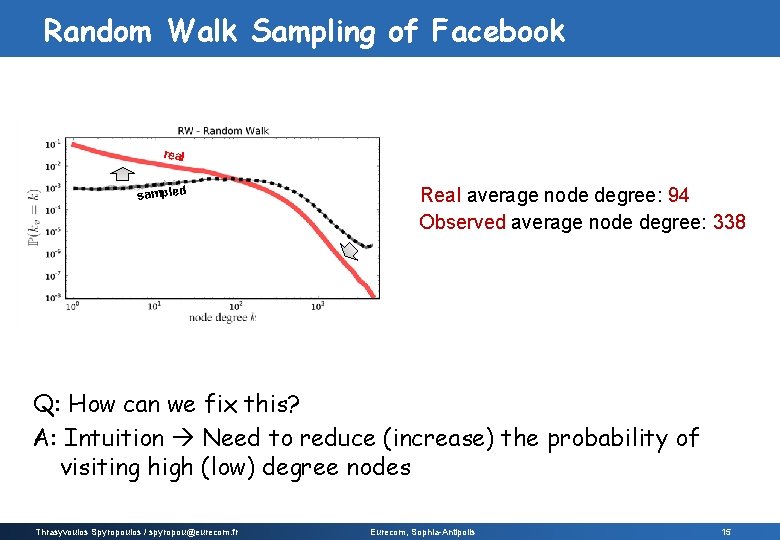
Random Walk Sampling of Facebook real sampled Real average node degree: 94 Observed average node degree: 338 Q: How can we fix this? A: Intuition Need to reduce (increase) the probability of visiting high (low) degree nodes Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 15

Markov Chain Monte Carlo (MCMC) Q: How should we modify the Random Walk? A: Markov Chain Monte Carlo theory Ø Original chain: move x y with prob Q(x, y) v Stationary distribution π(x) v Ø Desired chain: v Stationary distribution w(x) (for uniform sampling: w(x) = 1/N) Ø New transition probabilities Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 16

MCMC (2) Ø a(x, y): probability of accepting proposed move Q: How should we choose a(x, y) so as to converge to the desired stationary distribution w(x)? A: w(x) station. distr. w(x)P(x, y) = w(y)P(y, x) (for all x, y) Q: Why? Local balance (time-reversibility) equations w(x)Q(x, y)a(x, y) = w(y)Q(y, x)a(y, x) (denote b(x, y) = b(y, x)) a(x, y) ≤ 1 (probability) b(x, y) ≤ w(x)Q(x, y) b(x, y) = b(y, x) ≤ w(y)Q(y, x) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 17

MCMC for Uniform Sampling Ø w(x) = w(y) (= 1/n…doesn’t really matter) Ø Q(y, x)/Q(x, y) = kx/ky Ø Metropolis-Hastings random walk: Move to lower degree node always accepted v Move to higher degree node reject with prob related to degree ratio v Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 18

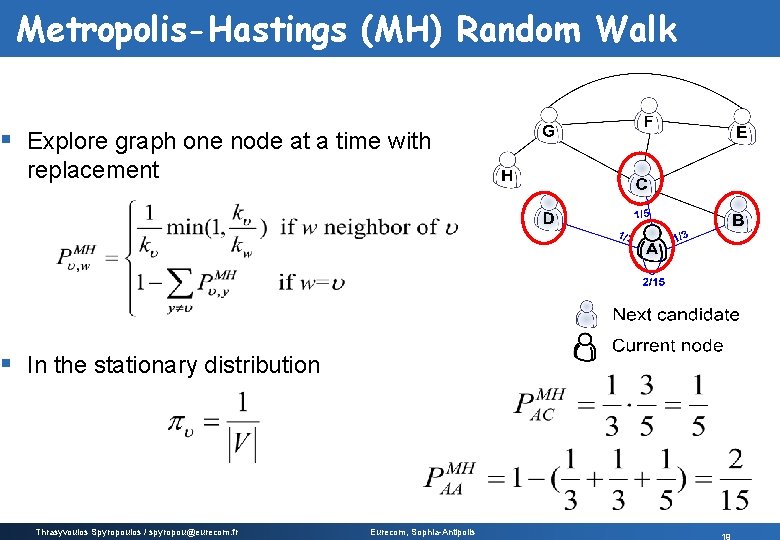
Metropolis-Hastings (MH) Random Walk § Explore graph one node at a time with replacement § In the stationary distribution Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

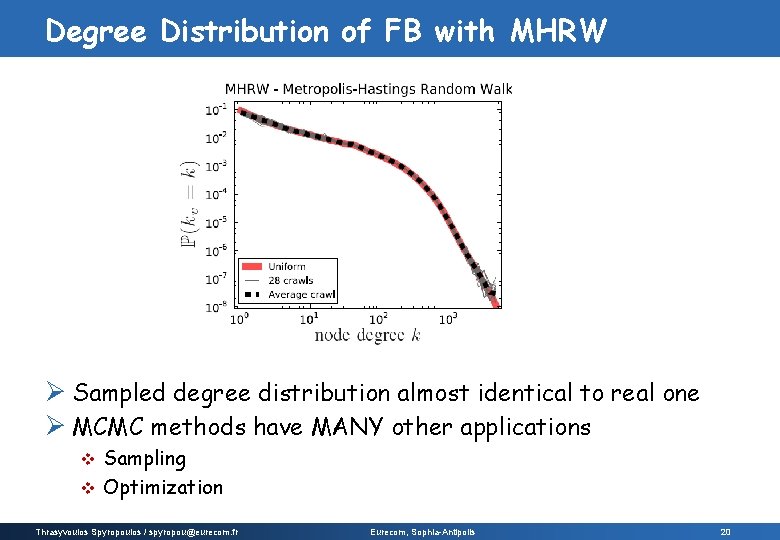
Degree Distribution of FB with MHRW Ø Sampled degree distribution almost identical to real one Ø MCMC methods have MANY other applications Sampling v Optimization v Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 20

Spectral Analysis of (ergodic) Markov Chains Ø If a Markov Chain (defined by transition matrix P) is ergodic (irreducible, aperiodic, and positive recurrent) P(n)ik πk and π = [π1, π2, …, πn] Q: But how fast does the chain converge? E. g. how many steps until we are “close enough” to π A: This depends on the eigenvalues of P The convergence time is also called the mixing time Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 21

Eigenvalues and Eigenvectors of matrix P Left Eigenvectors A row vector π is a left eigenvector for eigenvalue λ of matrix P iff πP = λπ Σk πk pki = λπi Right Eigenvectors A column vector v is a right eigenvector for eigenvalue λ of matrix P iff Pv = λv Σk pik vk = λvi Q: What eigenvalues and eigenvectors can we guess already? A: λ = 1 is a left eigenvalue with eigenvector π the stationary distr. λ = 1 is a right eigenvalue with eigenvector v=1 (all 1 s) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 22

Eigenvalues and Eigenvectors for 2 -state Chains Ø Both sets have non-zero solutions (P-λI) is singular v There exists v ≠ 0 such that (P-λI)v = 0 ÞDeterminant |P-λI| = 0 Þ(p 11 - λ)(p 22 - λ)-p 12 p 21 = 0 Þ λ 1=1, λ 2 = 1 – p 12 – p 21 (replace above and confirm using some algebra) v |λ 2| < 1 (normalized: π(1) to be a stationary distribution AND v(i) ∙π(i) = 1, ∀i) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 23

Diagonalization ÞEigenvalue decomposition: P = U Λ U-1 Q: What is P(n)? A: => Q: How fast does the chain converge to stationary distrib. ? A: It converges exponentially fast in n, as (λ 2)n Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 24

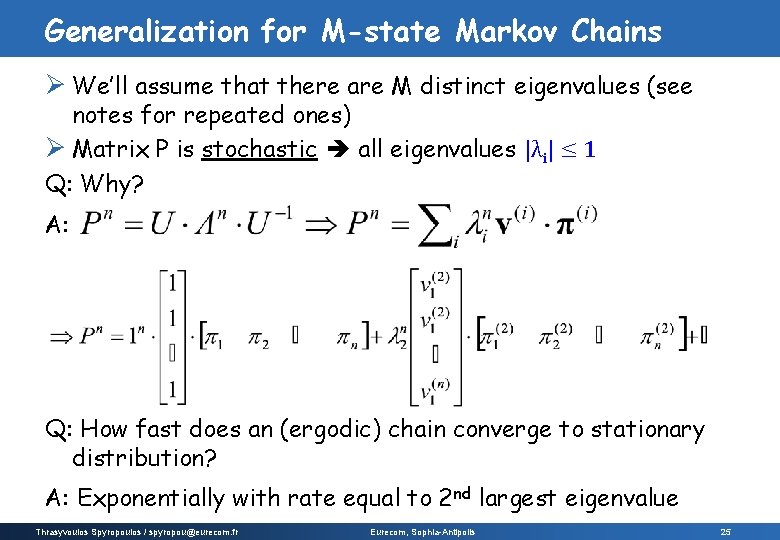
Generalization for M-state Markov Chains Ø We’ll assume that there are M distinct eigenvalues (see notes for repeated ones) Ø Matrix P is stochastic all eigenvalues |λi| ≤ 1 Q: Why? A: Q: How fast does an (ergodic) chain converge to stationary distribution? A: Exponentially with rate equal to 2 nd largest eigenvalue Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 25

Speed of Sampling on this Network? 26 Ø λ 2 (2 nd largest eigenvalue) related to (balanced) min-cut of the graph Ø The more “partitioned” a graph is into clusters with few links between them the longer the convergence time for the respective MC the slower the random walk search Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis 26

Community Detection - Clustering Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Device-to-Device Communication (e. g. Bluetooth or Wi. Fi Direct) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

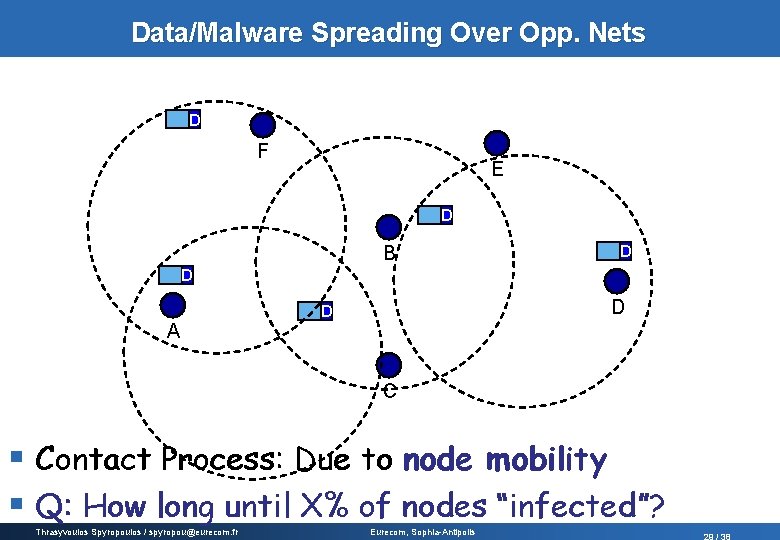
Data/Malware Spreading Over Opp. Nets D F E D B D D A D D C § Contact Process: Due to node mobility § Q: How long until X% of nodes “infected”? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

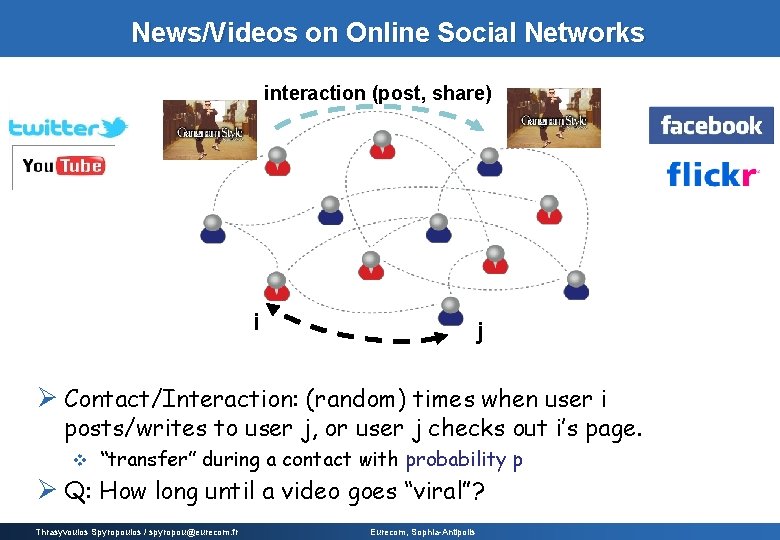
News/Videos on Online Social Networks interaction (post, share) i j Ø Contact/Interaction: (random) times when user i posts/writes to user j, or user j checks out i’s page. v “transfer” during a contact with probability p Ø Q: How long until a video goes “viral”? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Email Network § An email with a virus or worm § A graph showing which users send emails to whom § Pairwise contact process: (random) times of emails between i and j § Q: How long for the worm to spread? ? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Diffusion in networks: ER graphs http: //www. ladamic. com/netlearn/Net. Logo 501/ERDiffusion. htm l Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

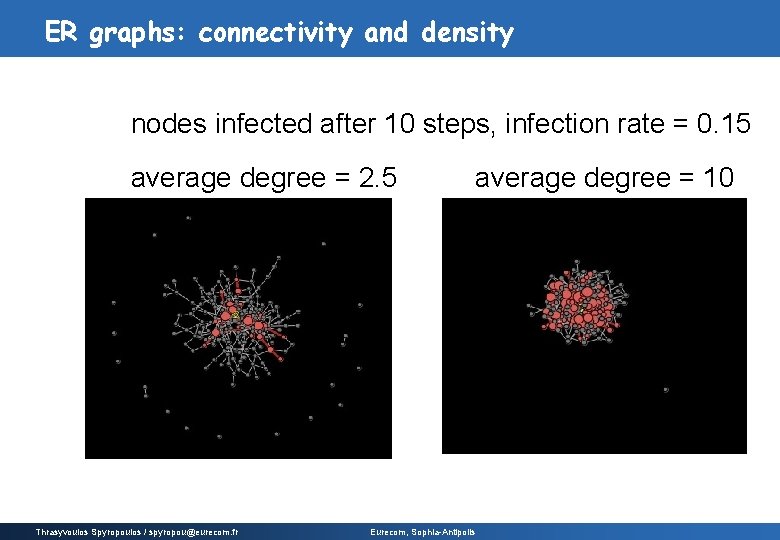
ER graphs: connectivity and density nodes infected after 10 steps, infection rate = 0. 15 average degree = 2. 5 Thrasyvoulos Spyropoulos / spyropou@eurecom. fr average degree = 10 Eurecom, Sophia-Antipolis

Quiz Q: Ø When the density of the network increases, diffusion in the network is faster v slower v unaffected v Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Diffusion in “grown networks” Ø nodes infected after 4 steps, infection rate = 1 preferential attachmentnon-preferential growth http: //www. ladamic. com/netlearn/Net. Logo 501/BADiffusion. html Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Quiz Q: Ø When nodes preferentially attach to high degree nodes, the diffusion over the network is faster v slower v unaffected v Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Diffusion in small worlds Ø What is the role of the long-range links in diffusion over small world topologies? http: //www. ladamic. com/netlearn/Net. Logo 4/Small. World. Diffusion. SIS. html Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Quiz Q: Ø As the probability of rewiring increases, the speed with which the infection spreads increases v decreases v remains the same v Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Analysis of Epidemics: The Usual Approach Assumption 1) Underlay Graph Fully meshed Assumption 2) Contact Process Poisson(λij), Indep. Assumption 3) Contact Rate λij = λ (homogeneous) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

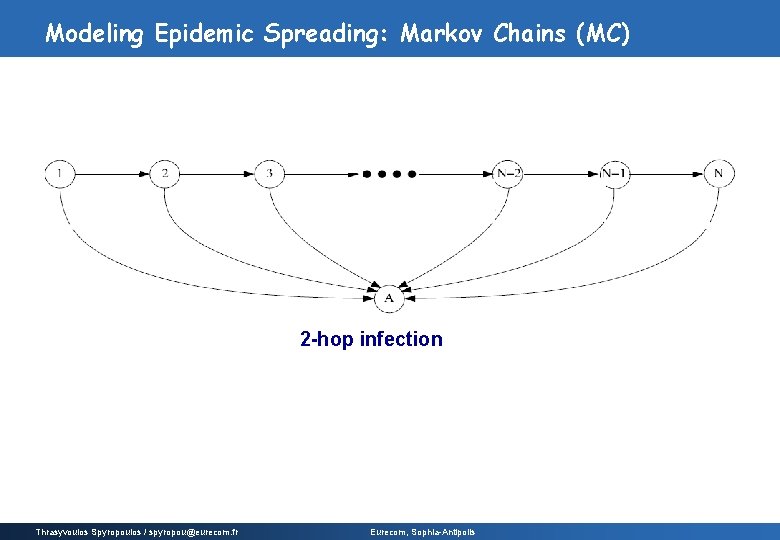
Modeling Epidemic Spreading: Markov Chains (MC) 2 -hop infection Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

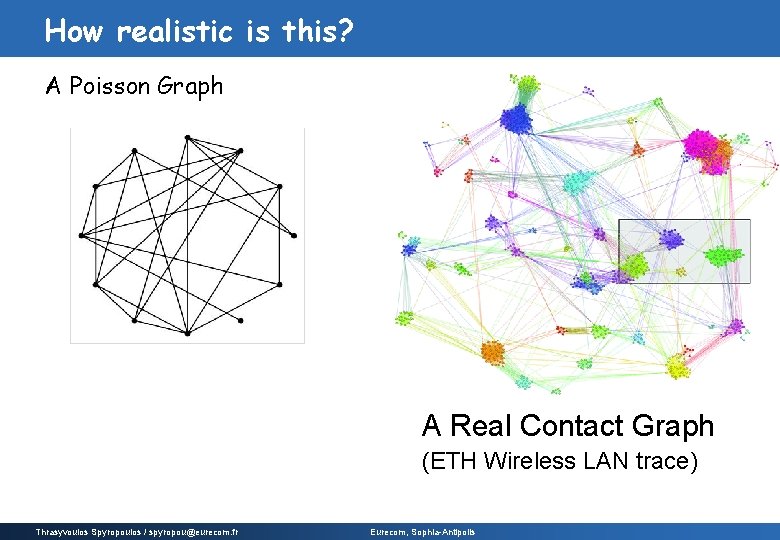
How realistic is this? A Poisson Graph A Real Contact Graph (ETH Wireless LAN trace) Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Arbitrary Contact Graphs Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

Bounding the Transition Delay Ø What are we really saying here? ? Ø Let a = 3 how can split the graph into a subgraph of 3 and a subgraph of N-3 node, by removing a set of edges whose weight sum is minimum? Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis

A 2 nd Bound on Epidemic Delay Ø Φ is a fundamental property of a graph Ø Related to graph spectrum, community structure Thrasyvoulos Spyropoulos / spyropou@eurecom. fr Eurecom, Sophia-Antipolis