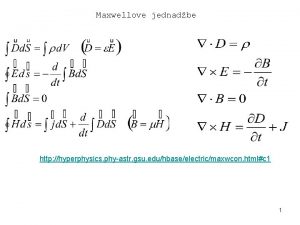QM Reminder C Nave gsu edu http hyperphysics






































- Slides: 53

QM Reminder

C Nave @ gsu. edu http: //hyperphysics. phy-astr. gsu. edu/hbase/quacon. html#quacon

Outline • Postulates of QM • Picking Information Out of Wavefunctions – Expectation Values – Eigenfunctions & Eigenvalues • Where do we get wavefunctions from? – Non-Relativistic – Relativistic • What good-looking Ys look like • Techniques for solving the Schro Eqn – Analytically – Numerically – Creation-Annihilation Ops

Postulates of Quantum Mechanics • The state of a physical system is completely described by a wavefunction Y. • All information is contained in the wavefunction Y • Probabilities are determined by the overlap of wavefunctions

Postulates of QM • Every measurable physical quantity has a corresponding operator. • The results of any individ measurement yields one of the eigenvalues ln of the corresponding operator. • Given a Hermetian Op with eigenvalues ln and eigenvectors Fn , the probability of measuring the eigenvalue ln is

Postulates of QM • If measurement of an observable gives a result ln , then immediately afterward the system is in state fn. • The time evolution of a system is given by • . corresponds to classical Hamiltonian


Picking Information out of Wavefunctions Expectation Values Eigenvalue Problems

Common Operators • Position r = ( x, y, z ) - Cartesian repn • Momentum • Total Energy • Angular Momentum L=rxp - work it out

Using Operators: A • Usual situation: Expectation Values • Special situations: Eigenvalue Problems the original wavefn a constant (as far as A is concerned)

Expectation Values • Probability Density at r • Prob of finding the system in a region d 3 r about r • Prob of finding the system anywhere

• Average value of position r • Average value of momentum p • Expectation value of total energy

Eigenvalue Problems Sometimes a function fn has a special property eigenvalue eigenfn Since this is simpler than doing integrals, we usually label QM systems by their list of eigenvalues (aka quantum numbers).

Eigenfns: 1 -D Plane Wave moving in +x direction Y(x, t) = A sin(kx-wt) or A cos(kx-wt) or A ei(kx-wt) • Y is an eigenfunction of Px • Y is an eigenfunction of Tot E • Y is not an eigenfunction of position X

Eigenfns: Hydrogenic atom Ynlm(r, q, f) • Y is an eigenfunction of Tot E • Y is an eigenfunction of L 2 and Lz • Y is an eigenfunction of parity units e. V

Eigenfns: Hydrogenic atom Ynlm(r, q, f) • Y is not an eigenfn of position X, Y, Z • Y is not an eigenfn of the momentum vector Px , Py , Pz • Y is not an eigenfn of Lx and Ly


Where Wavefunctions come from

Where do we get the wavefunctions from? • Physics tools – Newton’s equation of motion – Conservation of Energy – Cons of Momentum & Ang Momentum The most powerful and easy to use technique is Cons NRG.

Schrödinger Wave Equation Use non-relativistic formula for Total Energy Ops and http: //www-groups. dcs. st-and. ac. uk/~history/Mathematicians

Klein-Gordon Wave Equation Start with the relativistic constraint for free particle: Etot 2 – p 2 c 2 = m 2 c 4. p 2 = px 2 + py 2 + pz 2 [ Etot 2 – p 2 c 2 ] Y(r, t) = m 2 c 4 Y(r, t). a Monster to solve

Dirac Wave Equation Wanted a linear relativistic equation Etot 2 – p 2 c 2 = m 2 c 4 p = ( px , py , pz ) [ Etot 2 – p 2 c 2 - m 2 c 4 ] Y(r, t) = 0 Change notation slightly ~ P 4 = ( po , ipx , ipy , ipz ) [P 42 c 2 - m 2 c 4 ] Y(r, t) = 0 difference of squares can be factored ~ ( P 4 c + mc 2) (P 4 c-mc 2) and there are two options for how to do overall +/- signs 4 coupled equations to solve.

Time Dependent Schro Eqn Where H = KE + Potl E

ER 5 -5 Time Dependent Schro Eqn Where H = KE + Potl E

Time Independent Schro Eqn KE involves spatial derivatives only If Pot’l E not time dependent, then Schro Eqn separable ref: Griffiths 2. 1

Drop to 1 -D for ease


ER 5 -6 What Good Wavefunctions Look Like

Sketching Pictures of Wavefunctions Prob ~ Y* Y KE + V = Etot

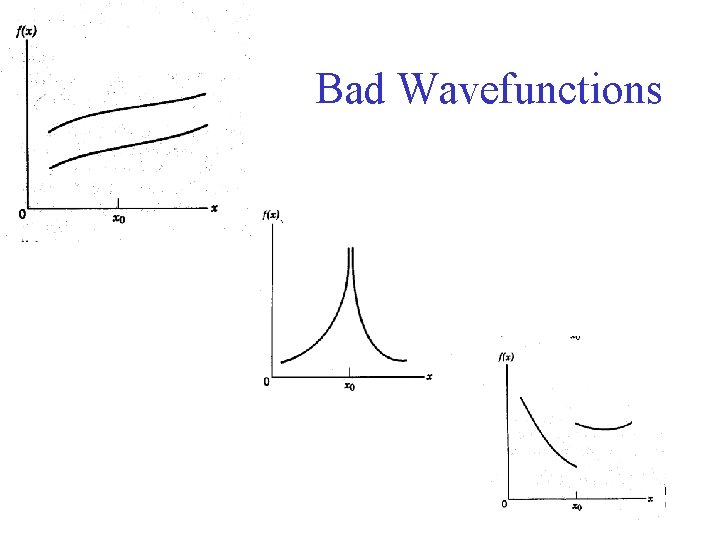
Bad Wavefunctions

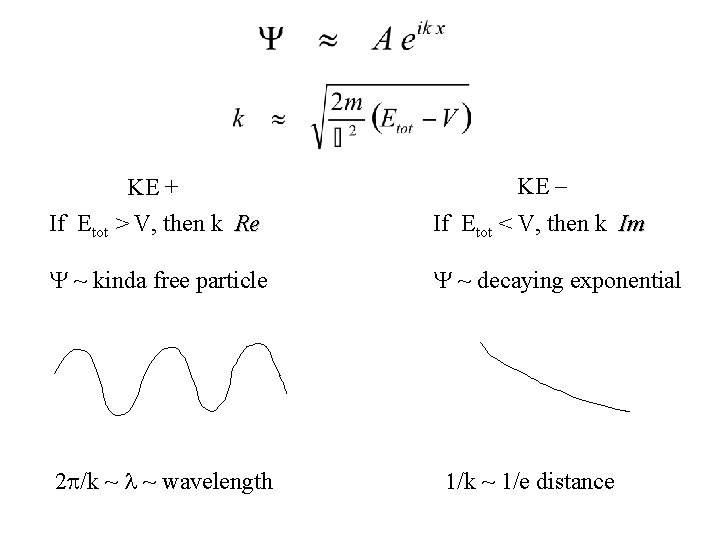
Sketching Pictures of Wavefunctions To examine general behavior of wave fns, look for soln of the form where k is not necessarily a constant (but let’s pretend it is for a sec) KE

KE - KE + If Etot > V, then k Re If Etot < V, then k Im Y ~ kinda free particle Y ~ decaying exponential 2 p/k ~ l ~ wavelength 1/k ~ 1/e distance

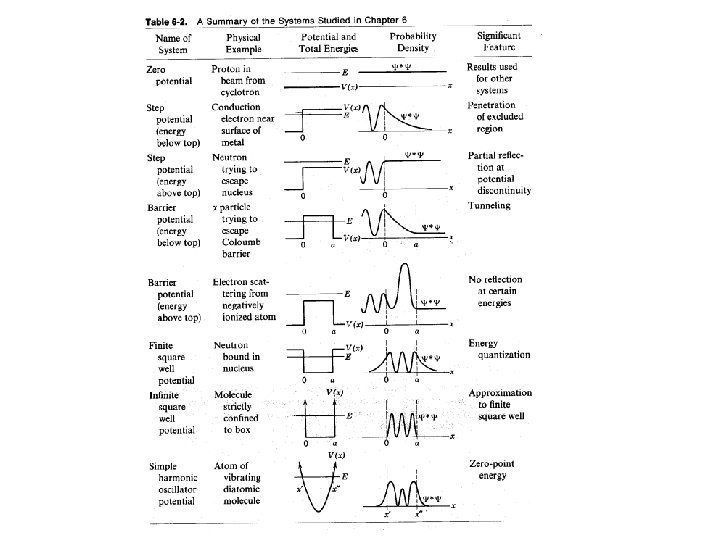
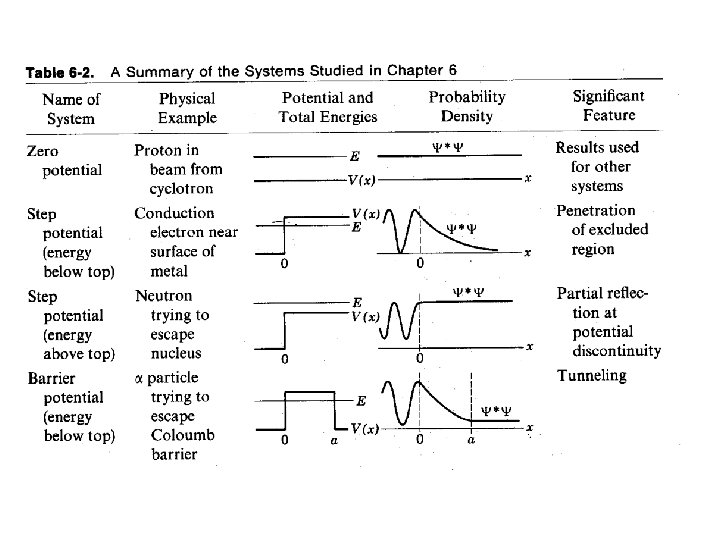
Sample Y(x) Sketches • • Free Particles Step Potentials Barriers Wells

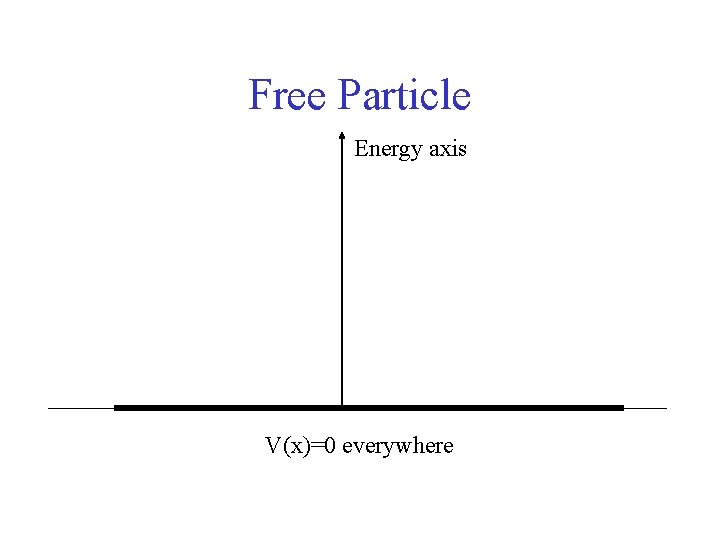
Free Particle Energy axis V(x)=0 everywhere

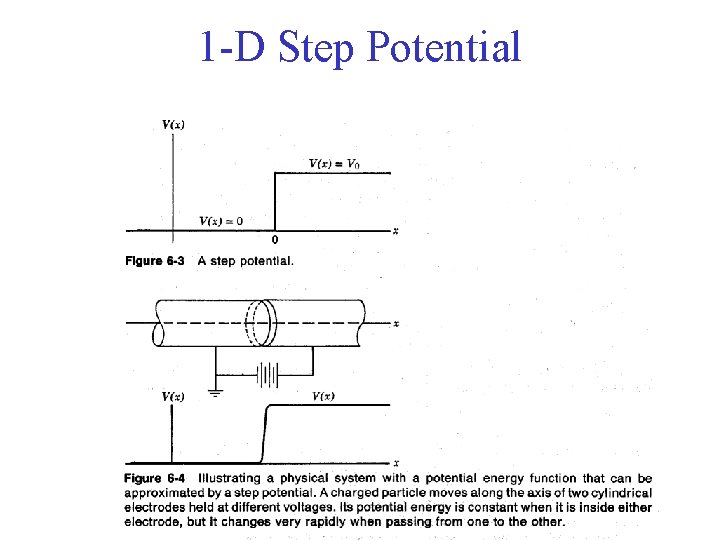
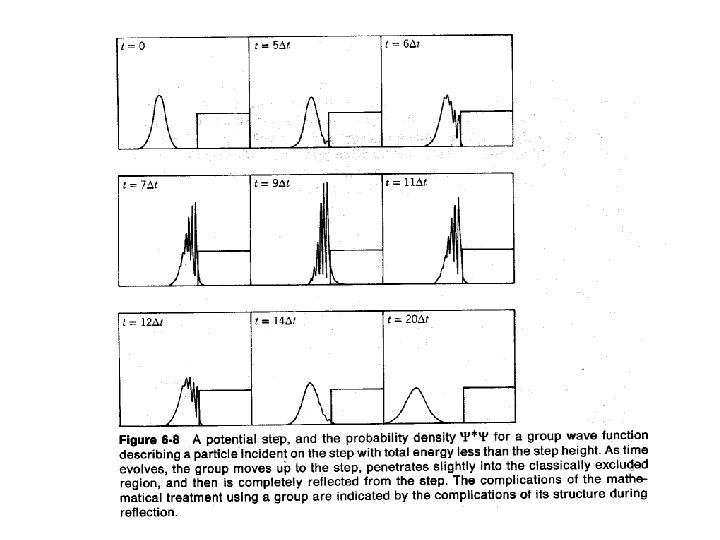
1 -D Step Potential


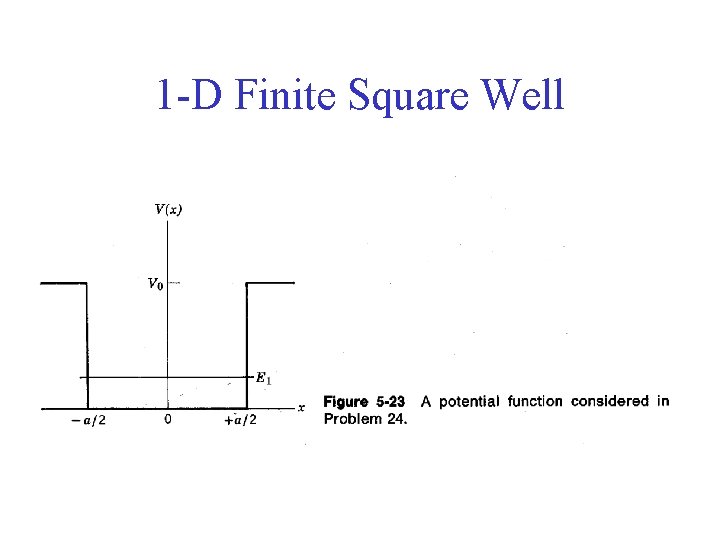
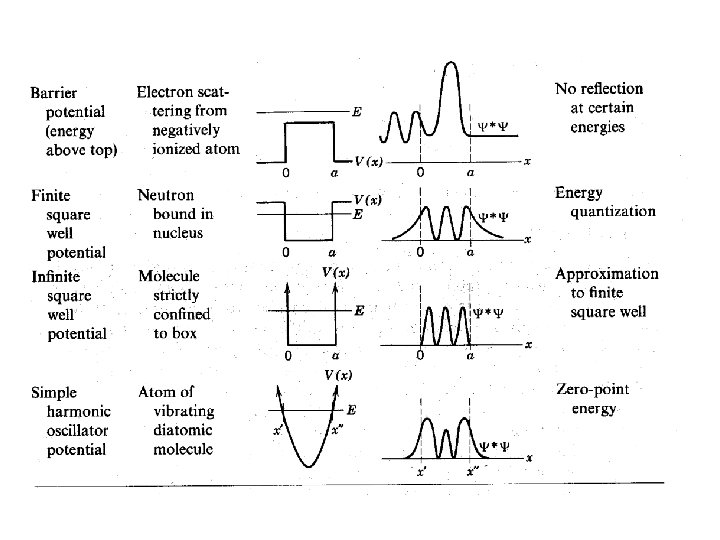
1 -D Finite Square Well

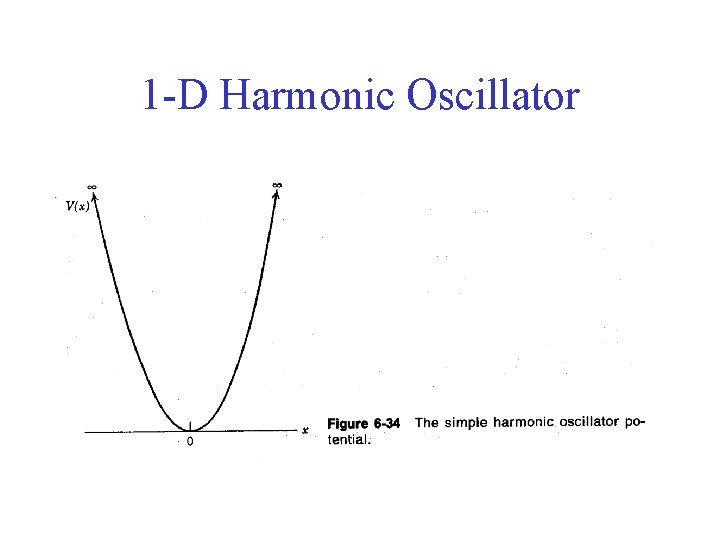
1 -D Harmonic Oscillator

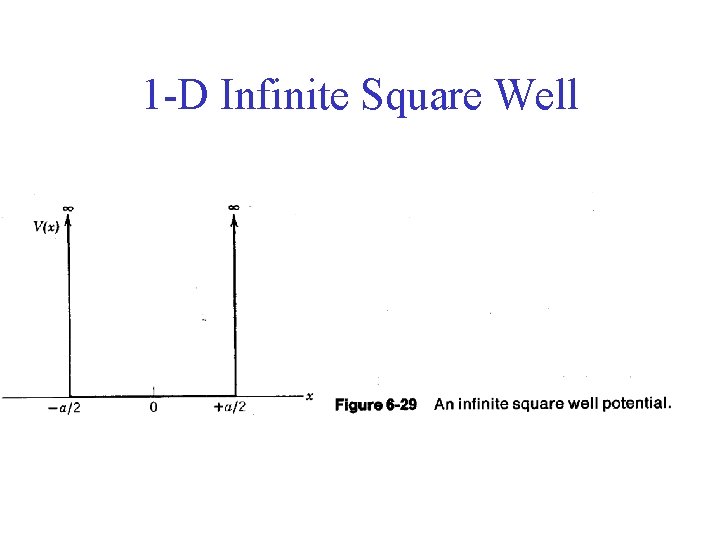
1 -D Infinite Square Well

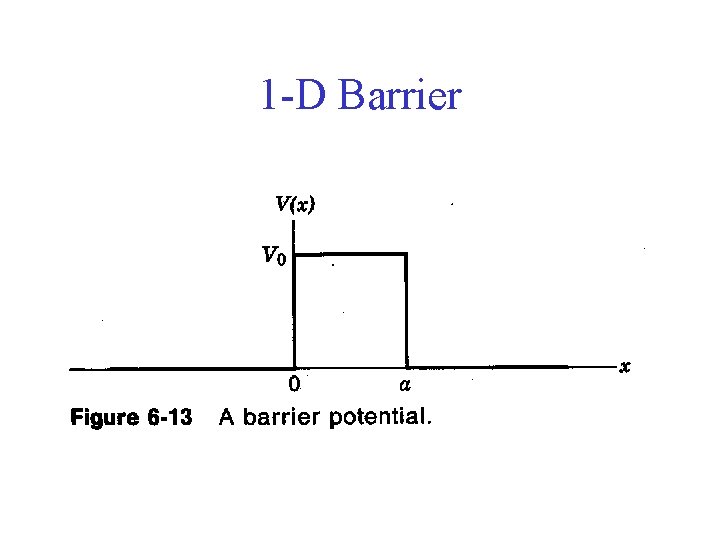
1 -D Barrier

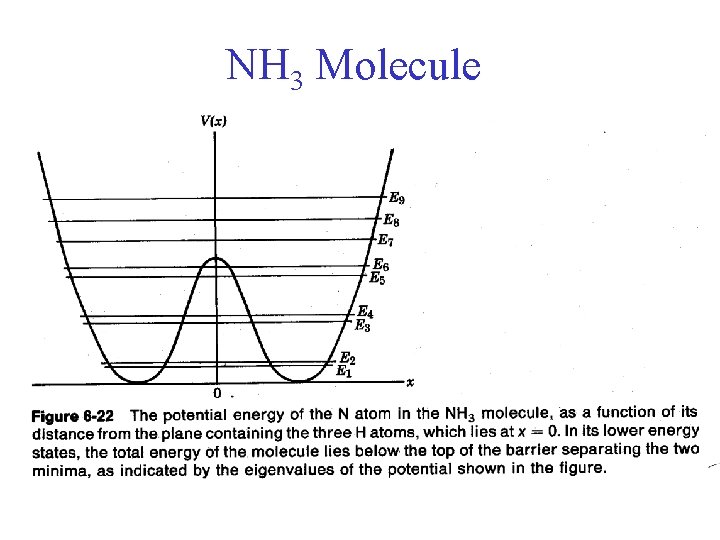
NH 3 Molecule

E&R Ch 5 Prob 23 Discrete or Continuous Excitation Spectrum ?

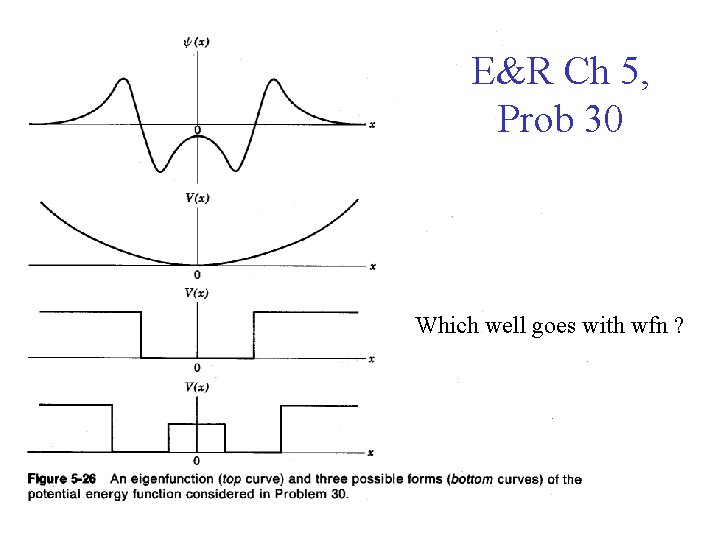
E&R Ch 5, Prob 30 Which well goes with wfn ?



Techniques for solving the Schro Eqn. • Analytically – Solve the Diffy. Q to obtain solns • Numerically – Do the Diffy. Q integrations with code • Creation-Annihilation Operators – Pattern matching techniques derived from 1 D SHO.

Analytic Techniques • Simple Cases – Free particle (ER 6. 2) – Infinite square well (ER 6. 8) • Continuous Potentials – 1 -D Simple Harmonic Oscillator (ER 6. 9, Table 6. 1, and App I) – 3 -D Attractive Coulomb (ER 7. 2 -6, Table 7. 2) – 3 -D Simple Harmonic Oscillator • Discontinuous Potentials – Step Functions (ER 6. 3 -7) – Barriers (ER 6. 3 -7) – Finite Square Well (ER App H)



Eigenfns: Bare Coulomb - stationary states Ynlm(r, q, f) or Rnl(r) Ylm(q, f) Simple/Bare Coulomb

Numerical Techniques ER 5. 7, App G • Using expectations of what the wavefn should look like… – – – – – Numerical integration of 2 nd order Diffy. Q Relaxation methods. . Joe Blow’s idea Willy Don’s idea Cletus’ lame idea. .

SHO Creation-Annihilation Op Techniques Define: If you know the gnd state wavefn Yo, then the nth excited state is:

Inadequacy of Techniques • Modern measurements require greater accuracy in model predictions. – Analytic – Numerical – Creation-Annihilation (SHO, Coul) • More Refined Potential Energy Fn: V() – Time-Independent Perturbation Theory • Changes in the System with Time – Time-Dependent Perturbation Theory
 Hyperphysics
Hyperphysics Panther involvement network
Panther involvement network Spectra of diatomic molecules
Spectra of diatomic molecules Methernitha
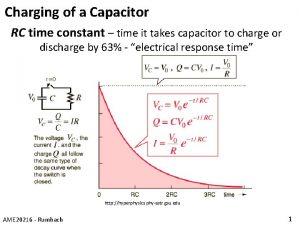
Methernitha Capacitor hyperphysics
Capacitor hyperphysics D spacing
D spacing Hyperphysics
Hyperphysics Blackbody radiation hyperphysics
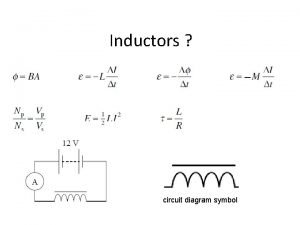
Blackbody radiation hyperphysics Inductor circuit symbol
Inductor circuit symbol Seth neddermeyer
Seth neddermeyer Hyperphysics
Hyperphysics Stir you up by way of reminder
Stir you up by way of reminder __________ always pairs with _________.
__________ always pairs with _________. Binder reminder
Binder reminder Pda language
Pda language Proactive patient outreach
Proactive patient outreach Thanks for the reminder.
Thanks for the reminder. Critical reminder
Critical reminder Pda
Pda I693 reminder letter
I693 reminder letter What dose advertisement mean
What dose advertisement mean Sql reminder
Sql reminder Adjectives for reminder
Adjectives for reminder Cohesive essay
Cohesive essay Pda reminder 1
Pda reminder 1 Growth mindset crumpled paper activity
Growth mindset crumpled paper activity Resolution of flowers for algernon
Resolution of flowers for algernon Computation symbol
Computation symbol Gsü otomasyon
Gsü otomasyon Gsu antivirus
Gsu antivirus Gsu university advisement center
Gsu university advisement center Gwinnett tech dual enrollment
Gwinnett tech dual enrollment Galileo gsu
Galileo gsu Gsu new student orientation
Gsu new student orientation Unm vlab
Unm vlab Gsu si
Gsu si Edu.sharif.edu
Edu.sharif.edu Egif umich
Egif umich Https://scratch.mit.edu.
Https://scratch.mit.edu. Http://www.openclass.chc.edu.tw
Http://www.openclass.chc.edu.tw Http // scratch.mit.edu/
Http // scratch.mit.edu/ Https //scratch.mit.edu
Https //scratch.mit.edu Teachertech.rice.edu
Teachertech.rice.edu Parabolic partial differential equation
Parabolic partial differential equation Http://weather.uwyo.edu/upperair/sounding.html
Http://weather.uwyo.edu/upperair/sounding.html Http sinhvien hufi
Http sinhvien hufi Http //www.phys.hawaii.edu/ teb/optics/java/slitdiffr/
Http //www.phys.hawaii.edu/ teb/optics/java/slitdiffr/ Http://learn.genetics.utah.edu/content/addiction/
Http://learn.genetics.utah.edu/content/addiction/ Https:scratch.mit.edu/
Https:scratch.mit.edu/ Faculty marshall usc advertising csv
Faculty marshall usc advertising csv Dendro.cnre.vt.edu photosynthesis chloroplast
Dendro.cnre.vt.edu photosynthesis chloroplast Www.learn.genetics.utah.edu
Www.learn.genetics.utah.edu Https // scratch.mit.edu
Https // scratch.mit.edu Http //2learner.hcmup.edu.vn
Http //2learner.hcmup.edu.vn