PREDICATES AND QUANTIFIERS Lecture 15 1 TERMINOLOGY REVIEW

PREDICATES AND QUANTIFIERS Lecture # 15 1

TERMINOLOGY REVIEW � Proposition: - A statement that is either true or false - Must always be one or the other! � Example: � “The sky is red” � Not a proposition: x + 3 > 4 � Boolean variable: - A variable (usually p, q, r, etc. ) that represents a proposition. 2

� Consider the following statements: x > 3, x = y +3, x + y = z � We can make propositions out of such statements �A predicate is a property that is affirmed or denied about the subject (in logic: we say “variables” or “arguments”) of a statement. “ x is greater then 3” subject 3 predicate

� To write in a predicate logic: “ x is greater then 3” subject predicate � We introduce a (functional) symbol for the predicate, and put the subject as an argument (to the functional symbol): P(x). The statement P(x) is also said to be propositional function. � Examples: • • 4 Father(x): unary predicate Brother(x, y): binary predicate Sum(x, y, z): ternary predicate P(x, y, z, …t): n-ary predicate

PROPOSITIONAL FUNCTIONS � Consider P(x) = x < 5 � P(x) has no truth values (x is not given a value) � P(1) is true �The proposition 1 < 5 is true � P(10) is false �The proposition 10 < 5 is false � Thus, value. 5 P(x) will create a proposition when given a

EXAMPLE � Let P(x) denote the statement “x > 3”. What are truth values of P(4) and P(2)? � SOLUTION: P(x) = x > 3 P(4) = 4 > 3 P(4) = True P(x) = x > 3 P(2) = 2 > 3 P(2) = False 6

EXAMPLES � Let P(x) = “x is a multiple of 5” � For � Let P(x) = x+1 > x � For � Let what values of x is P(x) true? P(x) = x + 3 � For 7 what values of x is P(x) true?

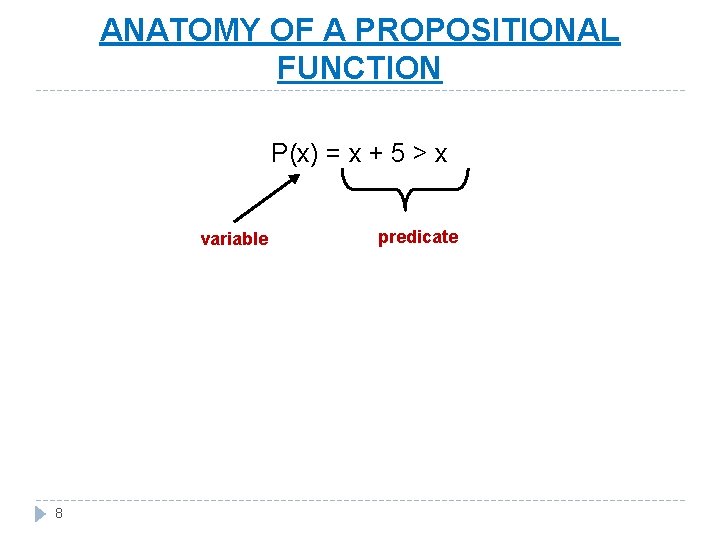
ANATOMY OF A PROPOSITIONAL FUNCTION P(x) = x + 5 > x variable 8 predicate

PROPOSITIONAL FUNCTIONS INVOLVING MULTIPLE VARIABLES � Functions with multiple variables: � P(x, y) = x + y == 0 � P(1, 2) is false, P(1, -1) is true � P(x, y, z) = x + y == z � P(3, 4, 5) is false, P(1, 2, 3) is true � P(x 1, x 2, x 3 9 … xn) = …

DEFINITION �A predicate is a sentence that contains a finite number of variables and becomes a statement when specific values are substituted for the variables. � The domain of a predicate variable is the set of all values that may be substituted in place of the variable. 10

UNIVERSE OF DISCOURSE � Consider the statement ‘x > 3’, does it make sense to assign to x the value ‘blue’? � Intuitively, the universe of discourse is the set of all things we wish to talk about; that is the set of all objects that we can sensibly assign to a variable in a propositional function. Referred to as Domain. � What would be the universe of discourse for the propositional function below be: Enrolled. CSE 235(x)=‘x is enrolled in CSE 235’ 11

QUANTIFIERS � When the variables in a propositional function are assigned values, the resulting statement becomes a proposition with a certain truth values. � However, there is another important way, called quantification, to create a proposition from a propositional function. � Quantification expresses the extent to which a predicate is true over a range of elements. 12

� In English, the words all, some, many, none and few are used in quantification. � We will focus on two types of quantification here � Universal Quantification � Existential Quantification 13

� The � It statement ‘x > 3’ is not a proposition becomes a proposition When we assign values to the argument: ‘ 4>3’ is false, ‘ 2<3’ is true, or � When we quantify the statement � � Two quantifiers � Universal quantifier for all the proposition is true for all possible values in the universe of discourse � Existential quantifier exists 14

UNIVERSAL QUANTIFIER � Definition: The universal quantification of a predicate P(x) is the proposition ‘P(x) is true for all values of x in the universe of discourse. ’ � Notation: We use the notation: x P(x), which is read ‘for all x’. � If the universe of discourse is finite, say {n 1, n 2, …, nk}, then the universal quantifier is simply the conjunction of the propositions over all the elements x P(x) P(n 1) P(n 2) … P(nk) 15

UNIVERSAL QUANTIFIER � Represented by an upside-down A: � It means “for all” � Let P(x) = x+1 > x � We can state the following: � x P(x) � English translation: “for all values of x, P(x) is true” � English translation: “for all values of x, x+1>x is true” 16

EXAMPLE � Let the universe be the real numbers. � Then, � Let x P(x) is true P(x) = x/2 < x � Not true for the negative � Thus, x P(x) is false � When numbers! the domain is all the real numbers � In order to prove that a universal quantification is true, it must be shown for ALL cases. � In order to prove that a universal quantification is false, it must be shown to be false for only ONE case 17

LOOP � Think � x �… of as a for loop: P(x), where 1 ≤ x ≤ 10 can be translated as … for ( x = 1; x <= 10; x++ ) is P(x) true? � If � 18 P(x) is true for all parts of the for loop, then x P(x) Consequently, if P(x) is false for any one value of the for loop, then x P(x) is false

REMEMBER � The truth value of x P(x) depends on the domain/universe of discourse! statement x P(x) is false. If and only If P(x) is not always true when x is in the domain. �A � One way to show that P(x) is not always true when x is in the domain is to find a counterexample. �A single counter example is all we need to establish that x P(x) is false. 19

EXAMPLE � Let Q(x) be the statement “x < 2”. What is the truth value of the quantification x Q(x), where the domain consists of all real numbers? � Solution: Q(x) is not true for every real number x Counter Example: Let x = 3 Q(3) is false Thus, x Q(x) is false. 20

EXAMPLE is the truth value of x P(x), where P(x) is the statement “x 2 < 10” and the domain consists of the � What positive integers not exceeding 4? � Solution: The statement x P(x) is the same as the conjunction P(1) P(2) P(3) P(4) P(1) is true P(2) is true P(3) is true P(4) is false P(4), which is the statement “ 42 < 10” is false, Thus, x P(x) is false. 21

EXAMPLE � a) What is the truth value of x (x 2 ≥ x), if the domain consists of all real numbers? b) What is the truth value of x (x 2 ≥ x), if the domain consists of all integers? a) Solution: The universal quantification (x 2 ≥ x) is not true for every real number x Counter Example: Let x = ½ (1/2)2 ≥ (1/2) is false 22

b) Solution: The universal quantification (x 2 ≥ x) is true for all integers. 23

EXISTENTIAL QUANTIFICATION � Definition: The existential quantification of a predicate P(x) is the proposition ‘There exists a value x in the universe of discourse such that P(x) is true. ’ � Notation: We use the notation: x P(x), which is read ‘there exists x’. � If the universe of discourse is finite, say {n 1, n 2, …, nk}, then the existential quantifier is simply the disjunction of the propositions over all the elements x P(x) P(n 1) P(n 2) … P(nk) 24

� Represented by an backwards E: � It means “there exists” � Let P(x) = x+1 > x � We � x can state the following: P(x) � English translation: “there exists (a value of) x such that P(x) is true” � English translation: “for at least one value of x, x+1>x is true” 25

EXAMPLE � Let P(x) = x+1 > x � There is a numerical value for which x+1>x �In fact, it’s true for all of the values of x! � Thus, x P(x) is true � In order to show an existential quantification is true, you only have to find ONE value � In order to show an existential quantification is false, you have to show it’s false for ALL values 26

EXAMPLE � Let P(x) be the statement “x > 3. ” What is the truth value of the quantification x P(x), where the domain consists of all real numbers? � Solution: P(x) is true for some values in domain Counter Example: Let x = 4 P(4) is true Thus, x P(x) is true. 27

EXAMPLE � Let Q(x) be the statement “x = x + 1. ” What is the truth value of the quantification x Q(x), where the domain consists of all real numbers? � Solution: Q(x) is false for every real number x. Counter Example: Let x = 6 Q(6) = 6 + 1 is false Thus, x Q(x) is false. 28

EXAMPLE is the truth value of x P(x), where P(x) is the statement “x 2 > 10” and the universe of discourse consists of � What the positive integers not exceeding 4? � Solution: The statement x P(x) is the same as the disjunction P(1) P(2) P(3) P(4) P(1) is false P(2) is false P(3) is false P(4) is true P(4), which is the statement “ 42 < 10” is true Thus, x P(x) is true 29

NOTE � Recall � Let that P(x) is a propositional function P(x) be “x == 0” � Recall that a proposition is a statement that is either true or false � P(x) is not a proposition � There are two ways to make a propositional function into a proposition: � Supply � For it with a value example, P(5) is false, P(0) is true � Provide � For 30 a quantification example, x P(x) is false and x P(x) is true Let the universe of discourse be the real numbers

QUANTIFIERS: Truth values � In general, when are quantified statements true or false? Statement True when… x P(x) False when. . . There is an x for which P(x) is true for every x P(x) is false There is an x for which P(x) is false for every x P(x) is true

UNIQUENESS QUANTIFIER � The Uniqueness quantifier, denoted by ! or 1. � Notation: � ! x P(x) [or 1 x P(x)] states “there exist a unique x such that P(x) is true” � Other phrases for uniqueness quantification include “there is exactly one” and “there is one and only one. ” 32

EXAMPLE � ! x (x - 1 = 0), where the domain is the set of real numbers. � Solution: (x - 1 = 0) is true for a unique real number. Counter Example: Let x = 1 (x - 1 = 0) is true Note: Generally, uniqueness quantifier is avoided. It is best to stick with existential and universal quantifier. 33

QUANTIFIERS WITH RESTRICTED DOMAINS � EXAMPLE: What do statements x < 0 (x 2 > 0), y ≠ 0 (y 3 ≠ 0) and z > 0 (z 2 =2) SOLUTION: The statement x < 0 (x 2 > 0) states that for every real number x with x < 0, x 2 > 0. That is, “the square of negative real number is positive. ” The statement is the same as: x (x < 0 34 → x 2 > 0).

statement y ≠ 0 (y 3 ≠ 0) states for every real number y with y ≠ 0, we have (y 3 ≠ 0). � The That is, “the cube of every nonzero real number is nonzero. ” This statement is equivalent to: y(y ≠ 0 → y 3 ≠ 0) 35

statement z > 0 (z 2 =2) states that there exist a real number z with z > 0 such that z 2 =2. � The That is, “There is a positive square root of 2. ” This statement is equivalent to: z (z > 0 z 2 =2). 36

NOTE: � The restriction of a universal quantification is the same as the universal quantification of a conditional statement. Example: x < 0 (x 2 > 0) is another way of expressing x (x < 0 → x 2 > 0) � The restriction of existential quantification is the same as the existential quantification of a conjunction. Example: 37 z > 0 (z 2 =2) is another way of

PRECEDENCE OF QUANTIFICATION � The quantifiers and have higher precedence than all logical operators from propositional calculus. � Example: x P(x) Q(x) is the disjunction of x P(x) and Q(x). � In other words, � It means ( x P(x)) Q(x) rather than x (P(x) Q(x)). 38

BINDING VARIABLES � When a quantifier is used on the variable x, we say that the occurrence of the variable is bound. � An occurrence of a variable that is not bound by a quantifier is said to be free. � The part of a logical expression to which a quantifier is applied is called the scope of this quantifier. 39

EXAMPLE � In the statement x (x + y =1), �The variable x is bound to by the existential quantification x. � The variable y is free because it is not bound by a quantifier. x (x + y =1), x is bound, but y is free. 40

EXAMPLE the statement x (P(x) Q(x)) x R(x), all variables are bound. � In scope of the first quantifier, x, is the expression (P(x) Q(x)) � The scope of the second quantifier, x is the expression R(x) � That is, the existential quantifier binds the variable x in P(x) Q(x) � 41 Universal quantifier binds the variable x in R(x). � The

EXAMPLES � ( x P(x)) Q(x) � The � ( x x in Q(x) is not bound; thus not a proposition P(x)) ( x Q(x)) � Both � ( x P(x) Q(x)) ( y R(y)) � All � ( x variables are bound; thus it is a proposition P(x) Q(y) ( y R(y)) � The 42 x values are bound; thus it is a proposition y in Q(y) is not bound; this not a proposition

BINDING VARIABLES � Let P(x, y) be x > y � Consider: x P(x, y) � This is not a proposition! � What is y? �If it’s 5, then x P(x, y) is false �If it’s x-1, then x P(x, y) is true � Note 43 that y is not “bound” by a quantifier

LOGICAL EQUIVALENCES INVOLVING QUANTIFIERS � Two statements S and T involving predicates and quantifiers are logically equivalent if and only if they have the same truth value regardless of the interpretation, i. e. regardless of � The meaning that is attributed to each propositional function. � The domain of discourse. � Notation: use the notation S T to indicate that two statements S and T involving predicates and quantifiers are logically equivalent. � We 44

EXAMPLE x (P(x) Q(x)) logically equivalent to x P(x) x Q(x)? where the same domain is used throughout. � Is � Solution: � Use � If two steps x (P(x) Q(x)) is true, then x P(x) x Q(x) is true � Proof: Suppose x (P(x) Q(x)) is true. Then if a is in the domain, P(a) Q(a) is true, So P(a) is true and Q(a) is true. � So, if a is in the domain P(a) is true, which is the same as x P(x) is true; and similarly, we get that x P(x) is true 45

TRANSLATING FROM ENGLISH INTO LOGICAL EXPRESSIONS � Example: Express the statement using predicates and quantifiers. “Every student in this class has studied calculus” Solution: � Step 1: First we rephrase the statement so that we can clearly identify the appropriate quantifiers to use. “For every student in this class, that student has studied calculus. ” � Step 46 2: Introduce a variable x “For every student x in this class, x has studied calculus”

� Step 3: Introduce C(x) = x has studied calculus. Domain = Students in the class. Step 4: x C(x) 47

EXAMPLE � Express the statement using predicates and quantifiers. “For every person x, If person x is a student in this class then x has studied calculus. ” Solution: � Step 1: � Step 2: � Step 3: Introduce S(x) and C(x) S(x) = Person x is in the class. C(x) = x has studied Calculus. Domain = Students in the class. � Step 4: x (S(x) → C(x)) 48

EXAMPLE � Express the statement using predicates and quantifiers. “Some student in this class has visited Mexico” Solution: � Step 1: First we rephrase the statement so that we can clearly identify the appropriate quantifiers to use. “There is a student in this class with the property that the student has visited Mexico” � Step 2: Introduce a variable x “There is a student x in this class having the property that x has visited Mexico” 49

� Step 3: Introduce M(x) = x has visited Mexico. Domain = Students in the class. Step 4: x M(x) 50

EXAMPLE � Express the statement using predicates and quantifiers. “There is a person x having the properties that x is a student in this class and x has visited Mexico. ” Solution: � Step 1: � Step 2: � Step 3: Introduce S(x) and M(x) S(x) = x is a student in this class. M(x) = x has visited Mexico. Domain = All person. � Step 4: x (S(x) M(x)) 51

EXAMPLE � Express the statement using predicates and quantifiers. “For every x in this class, x has the property that x has visited Mexico or x has visited Canada. ” Solution: � Step 1: � Step 2: � Step 3: Introduce C(x) and M(x) C(x) = x has visited Canada. M(x) = x has visited Mexico. Domain = All people. � Step 4: x (C(x) M(x)) 52

EXAMPLE � Express the statement using predicates and quantifiers. “For every person x, if x is a student in this class, then x has visited Mexico or x has visited Canada. ” Solution: � Step 1: � Step 2: � Step 3: Introduce S(x) and M(x) S(x) = x is a student in this class. C(x) = x has visited Canada. M(x) = x has visited Mexico. Domain = student in the class. � Step 4: x (S(x) → (C(x) M(x))). 53

EXAMPLES FROM LEWIS CARROL � Consider these statements. The first two are called premises and the third is called the conclusion. The entire set is called an argument. “All lions are fierce. ” “Some lions do not drink coffee. ” Therefore, “Some fierce creatures do not drink coffee. ” 54

SOLUTION � Let P(x) = “x is a lion. ” Q(x) = “x is fierce. ” R(x) = “x drinks coffee. ” Domain = Assume all creatures. � We can express these statements as: � “All lions are fierce. ” � x (P(x) → Q(x)). 55

� “Some lions do not drink coffee. ” x (P(x) ¬R(x)). � “Some fierce creatures do not drink coffee. ” x (Q(x) ¬R(x)). 56

MORE EXAMPLES � Translate the statements: � “All hummingbirds are richly colored” � “No large birds live on honey” � “Birds that do not live on honey are dull � “Hummingbirds are small” in color” � Solution: Assign propositional functions Let P(x) = “x is a hummingbird” Q(x) = “x is large” R(x) = “x lives on honey” S(x) = “x is richly colored” Let our universe of discourse be all birds 57

� Translate the statements: � Assume that “small” is the same as “not large” and that “dull in color” is the same as “not richly colored” � “All hummingbirds � x (P(x)→S(x)) are richly colored” � “No large birds live on honey” �¬ x (Q(x) R(x)) �Alternatively: x (¬Q(x) ¬R(x)) � “Birds that do not live on � x (¬R(x) → ¬S(x)) honey are dull in color” � “Hummingbirds are small” � x (P(x) → ¬Q(x)) 58

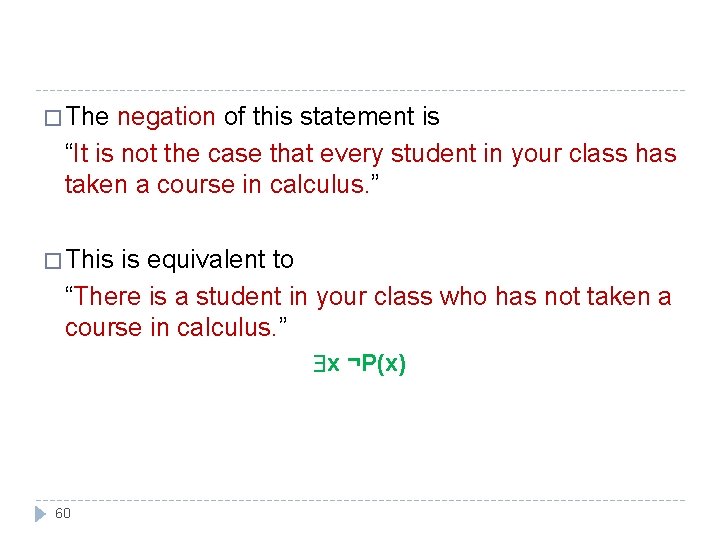
NEGATING QUANTIFIED EXPRESSIONS � Consider the statement: “Every student in your class has taken a course in calculus. ” P(x) = x has taken a course in calculus. Domain = Students in your class. x P(x) 59

� The negation of this statement is “It is not the case that every student in your class has taken a course in calculus. ” � This is equivalent to “There is a student in your class who has not taken a course in calculus. ” x ¬P(x) 60

� This example illustrate the following logical equivalence: ¬ x P(x) x ¬P(x) 61

NOTE note that ¬ x P(x) is true if and only if x P(x) is false. � First that x P(x) is false if and only if there is an element x in domain for which P(x) is false. � Note � Finally, note that there is an element x in the domain for which ¬ P(x) is true if and only if x ¬P(x) is true. � Putting these steps together, we can conclude that: ¬ x P(x) is true if and only if x ¬P(x) is true. 62

follows that ¬ x P(x) and x ¬P(x) are logically equivalent. � It 63

� Another example illustrate that following logical equivalence: ¬ x Q(x) x ¬Q(x) 64

EXAMPLE � What are the negations of the statements: “There is an honest politician” � Solution: H(x) = x is a honest. Domain = all politician x H(x) The negation of this statement is ¬ x H(x) = x ¬H(x) “Every politician is dishonest. ” 65

EXAMPLE � What are the negations of the statements: “All Americans eat cheeseburgers” � Solution: C(x) = x eats cheeseburgers. Domain = all Americans x C(x) The negation of this statement is ¬ x C(x) = x ¬C(x) “Some Americans does not eat cheeseburgers. ” 66

EXAMPLE � What are negations of the statement: x (x 2 > x) � Solution: The negation of x (x 2 > x) is the statement ¬ x (x 2 > x) = x ¬(x 2 > x) This can be re-written as: x (x 2 ≤ x) 67

EXAMPLE � What are negations of the statement: x (x 2 = 2) � Solution: The negation of x (x 2 = 2) is the statement ¬ x (x 2 = 2) = x ¬(x 2 = 2) This can be re-written as: x (x 2 ≠ 2) 68

EXMPLE that ¬ x (P(x)→Q(x)) and x (P(x) ¬Q(x)) are logically equivalent. � Show � Solution: ¬ x (P(x)→Q(x)) x ¬(P(x)→Q(x)) Given De Morgan’s law for universal quantifiers x ¬(¬P(x) Q(x)) As we know that p → q = ¬p q x (¬(¬P(x)) ¬Q(x)) De-Morgan’s law x (P(x) ¬Q(x)) Double Negation law R. H. S 69

EXMPLE � Express the negation of x y. P(x, y) x y. Q(x, y). � Solution: ¬( x y. P(x, y) x y. Q(x, y)) ¬( x y. P(x, y) ¬ x y. Q(x, y) x¬ y. P(x, y) x¬ y. Q(x, y) x y ¬P(x, y) x y ¬Q(x, y) 70 Given De Morgan’s law De-Morgan’s law

LOGIC PROGRAMMING � An important type of programming language is designed to reason using the rules of predicate logic. � Prolog (Programming in Logic) � Developed in 1970 s by computer scientists working in the area of artificial intelligence. 71