Quantifiers and Negation Predicates Predicate Will define function












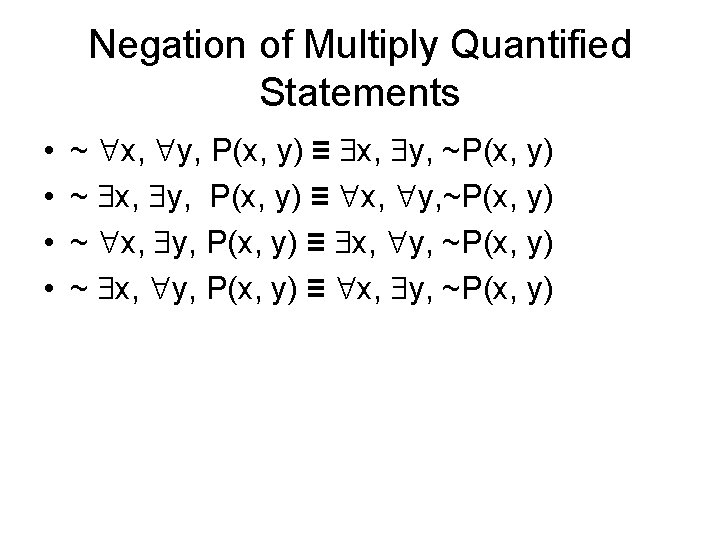




- Slides: 17

Quantifiers and Negation Predicates

Predicate • Will define function. • The domain of a function is the set from which possible values may be chosen for the argument of the function. • A predicate is a function whose possible values are True and False.

Universal Quantifier • The universal quantifier. • Upside down A. • “For All”

Universal Quantifier • Let P(x) be a predicate with domain D. • A universal statement is a statement in the form “ x, P(x)”. It is true iff P(x) is true for all x in D. It is false iff P(x) is false for at least one x in D. • A value of x which shows that P(x) is false is called a counterexample to the universal statement.

Universal Quantifier Examples • Let D = {1, 2, 3, 4, 5}. x, x² >= x • Let D=Reals. x Reals, x² >= x • Let D= Natural numbers. Let P(x)=x is prime, E(x)=x is even. x E(x) x P(x) x (E(x) V E(x+1))

Existential Quantifier • Existential quantifier. • Backwards E. • There Exists

Existential Quantifier • Let P(x) be a predicate with domain D. • An existential statement is a statement in the form “ x, P(x)”. It is true iff P(x) is true for at least one x in D. It is false iff P(x) is false for all x in D. • Examples: D=Integers, m, m² = m D = {5, 6, 7, 8, 9}, m, m² = m

Universal Conditional Statement • Universal conditional statement x, (P(x) Q(x)) Example: D=Reals. x, (x > 2 x 2 > 4) • A universal conditional statement is vacuously true or true by default iff P(x) is false for every x in D. i. e. ~ x D, P(x) iff x D (P(x) Q(x)) is vacuously true.

Universal Conditional Statement Examples: D=Natural numbers. E(x)=x is even. P(x)=x is prime x (E(x) ~E(x+1)) x ((E(x) Λ x > 2) ~P(x)) x (P(x) ~E(x))

Negation of Quantified Statements • ~ ( x D, P(x)) ≡ x D, ~P(x) • ~( x D, P(x)) ≡ x D, ~P(x) • ~ x D, P(x) Q(x) ≡ x D, ~(P(x) Q(x)) ≡ x D, P(x) ~Q(x)

Multiply Quantified Statements • Let the D=Integers. Let P(x, y) = y<x. • There exists a number x, there exists a number y, such that y<x x, y, P(x, y) ≡ y, x, P(x, y) True (both True) • For all numbers x, for all numbers y, y < x x, y, P(x, y) ≡ y, x, P(x, y) True (both False)

Multiply Quantified Statements • For all numbers x, there exists a number y such that x < y x, y, P(x, y) True • There exists a number y such that for all numbers x, x < y y, x, P(x, y) False • x, y, P(x, y) ≡ y, x, P(x, y) False
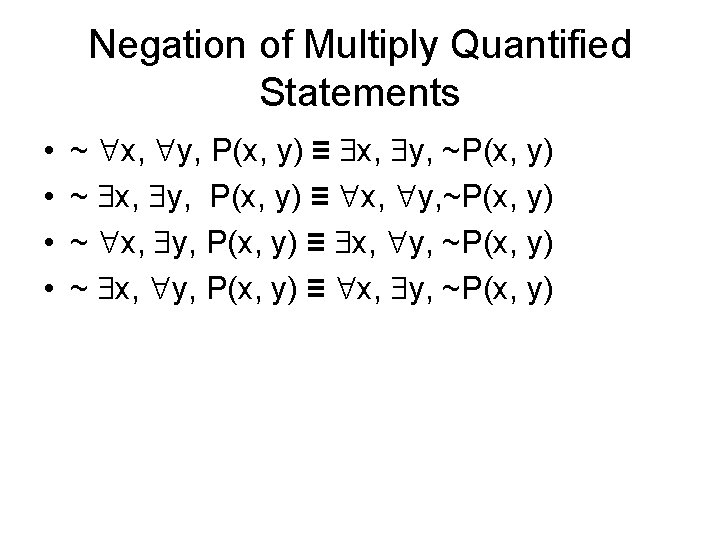
Negation of Multiply Quantified Statements • • ~ x, y, P(x, y) ≡ x, y, ~P(x, y)

Example a) Symbolize: The sum of any two even integers is even. b) Negate it.

Example Solution • Let E(x)=“x is even”. • Let E(x, y)=“x+y is even”. • Let the domain be the Integers. a) x, y, E(x)^E(y) E(x, y) b) x, y, E(x) ^ E(y) ^ ~E(x, y)

Which of the following is true? x D, (P(x) Q(x)) ≡ ( x D, P(x)) ( x D, Q(x))

, , Λ, ν Let P(x) be a predicate. Let D={x 1, x 2, …, xn} be the domain of x. • x D, P(x)≡P(x 1) Λ P(x 2)Λ…ΛP(xn) • x D, P(x) ≡P(x 1) ν P(x 2)ν…νP(xn)