Practical Model Selection and Multimodel Inference using R















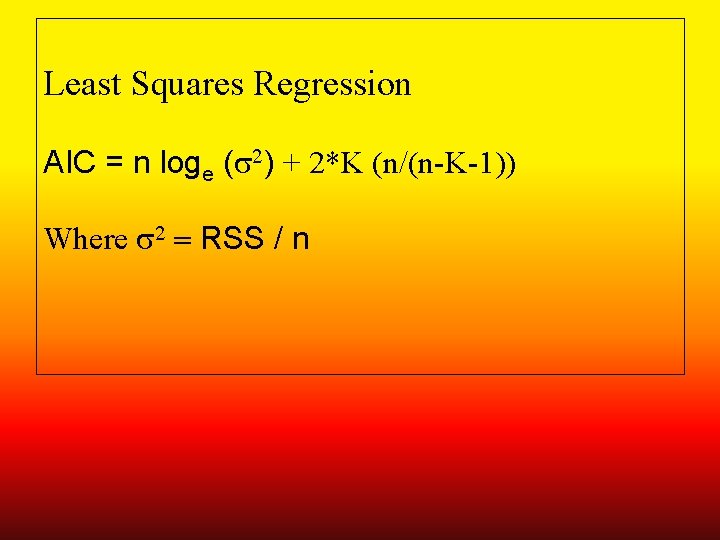





- Slides: 34

Practical Model Selection and Multi-model Inference using R Modified from on a presentation by : Eric Stolen and Dan Hunt

Theory • This is the link with science, which is about understanding how the world works

Indigo Snake Habitat selection David R. Breininger, M. Rebecca Bolt, Michael L. Legare, John H. Drese, and Eric D. Stolen Source: Journal of Herpetology, 45(4): 484 -490. 2011. – Animal perception – Evolutionary Biology – Population Demography http: //www. seaworld. org/animal-info/animal-bytes/spooky-safari/eastern-indigo-snake. htm

Hypotheses • To use the Information-theoretic toolbox, we must be able to state a hypothesis as a statistical model (or more precisely an equation which allows us to calculate the maximum likelihood of the hypothesis) http: //www. seaworld. org/animal-info/animal-bytes/spooky-safari/eastern-indigo-snake. htm

Multiple Working Hypotheses • • We operate with a set of multiple alternative hypotheses (models) The many advantages include safeguarding objectivity, and allowing rigorous inference. Chamberlain (1890) Strong Inference - Platt (1964) Karl Popper (ca. 1960)– Bold Conjectures

Deriving the model set • • This is the tough part (but also the creative part) much thought needed, so don’t rush collaborate, seek outside advice, read the literature, go to meetings… How and When hypotheses are better than What hypotheses (strive to predict rather than describe)

Models – Indigo Snake example David R. Breininger, M. Rebecca Bolt, Michael L. Legare, John H. Drese, and Eric D. Stolen Source: Journal of Herpetology, 45(4): 484 -490. 2011. • • • Study of indigo snake habitat use Response variable: home range size ln(ha) SEX Land cover – 2 -3 levels (l. C 2) weeks = effort/exposure Science question: “Is there a seasonal difference in habitat use between sexes? ”

Models – Indigo Snake example SEX land cover type (lc 2) weeks SEX + lc 2 SEX + weeks llc 2 + weeks SEX + lc 2 + SEX * lc 2 SEX + lc 2 + weeks + SEX * lc 2 http: //www. herpnation. com/hn-blog/indigo-snake-survivaldemographics/? simple_nav_category=john-c-murphy

Models – Indigo Snake example SEX land cover type (lc 2) weeks SEX + lc 2 SEX + weeks llc 2 + weeks SEX + lc 2 + SEX * lc 2 SEX + lc 2 + weeks + SEX * lc 2

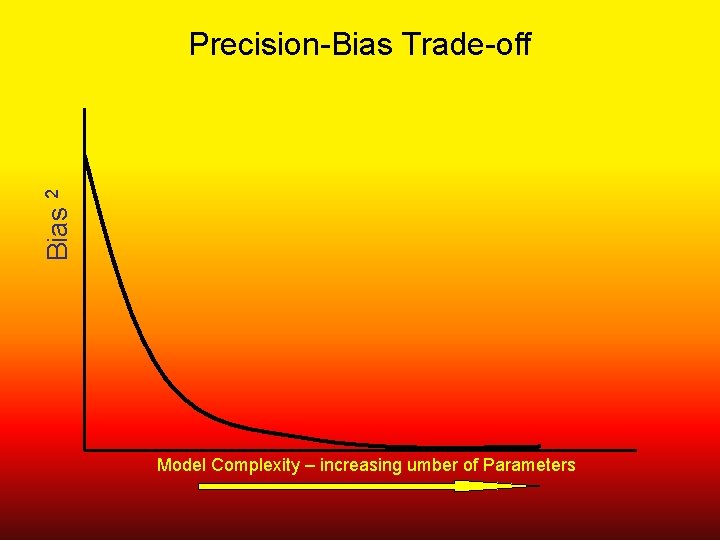
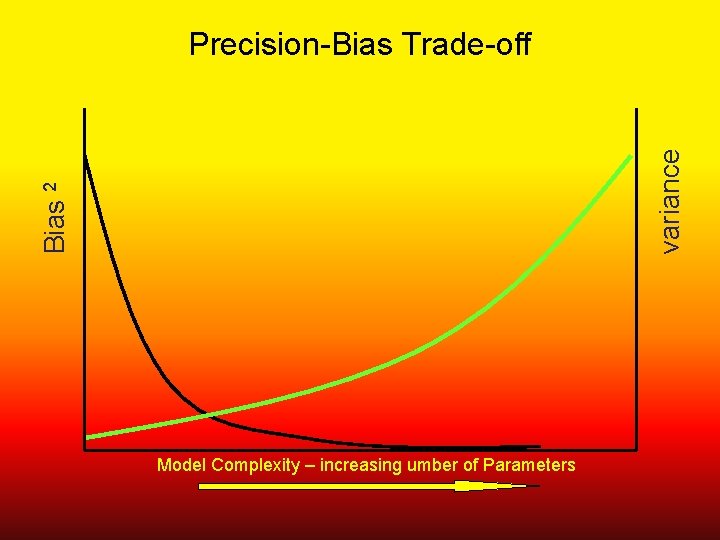
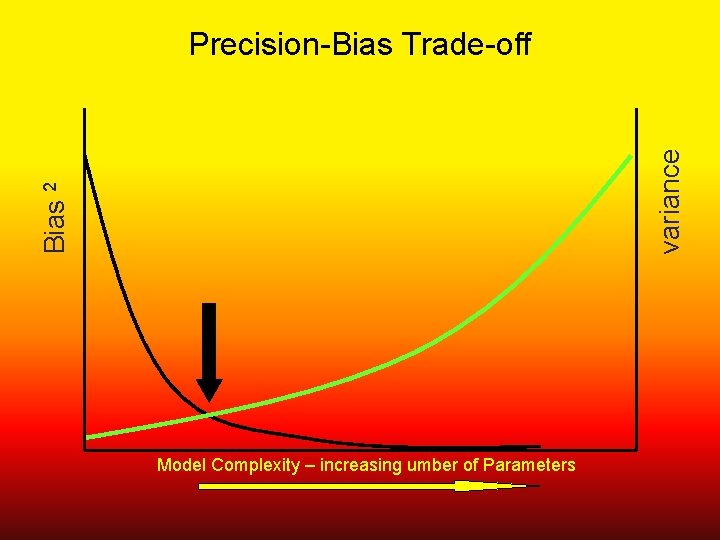
Modeling • Trade-off between precision and bias • Trying to derive knowledge / advance learning; not “fit the data” • Relationship between data (quantity and quality) and sophistication of the model

Bias 2 Precision-Bias Trade-off Model Complexity – increasing umber of Parameters

Bias 2 variance Precision-Bias Trade-off Model Complexity – increasing umber of Parameters

Bias 2 variance Precision-Bias Trade-off Model Complexity – increasing umber of Parameters

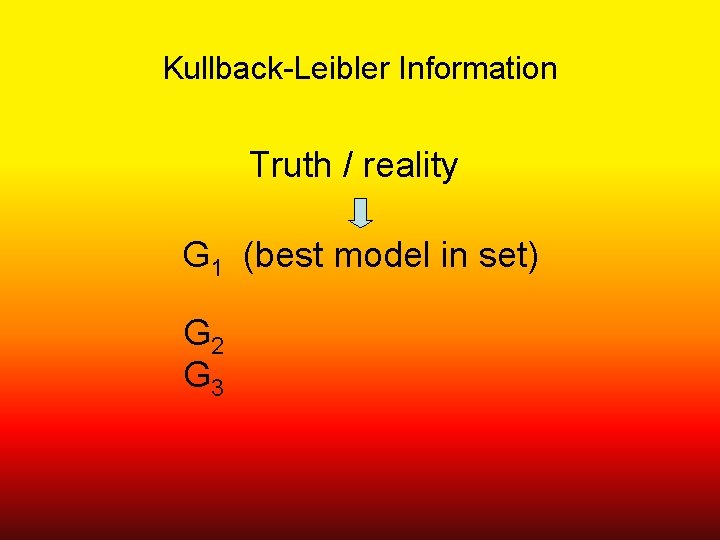
Kullback-Leibler Information • Basic concept from Information theory • The information lost when a model is used to represent full reality • Can also think of it as the distance between a model and full reality

Kullback-Leibler Information Truth / reality G 1 (best model in set) G 2 G 3

Kullback-Leibler Information Truth / reality G 1 (best model in set) G 3 G 2

Kullback-Leibler Information Truth / reality G 1 (best model in set) G 3 G 2

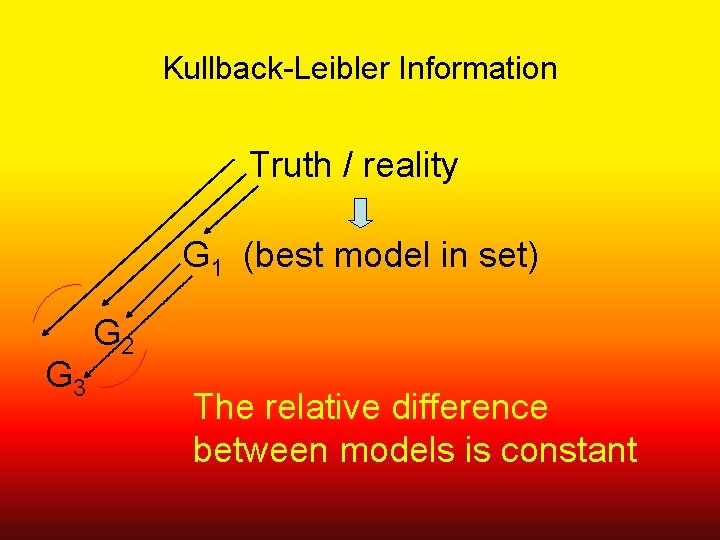
Kullback-Leibler Information Truth / reality G 1 (best model in set) G 3 G 2 The relative difference between models is constant

Akaike’s Contributions • Figured out how to estimate the relative Kullback -Leibler distance between models in a set of models • Figured out how to link maximum likelihood estimation theory with expected K-L information • An (Akaike’s) Information Criteria • AIC = -2 loge (L{modeli }| data) + 2 K

AICci = -2*loge (Likelihood of model i given the data) + 2*K (n/(n-K-1)) or = AIC + 2*K*(K+1)/(n-K-1) (where K = the number of parameters estimated and n = the sample size)

AICcmin = AICc for the model with the lowest AICc value Di = AICci– AICcmin

wi =Prob{gi | data} Model Probability (model probabilities) evidence ratio of model i to model j = wi / wj
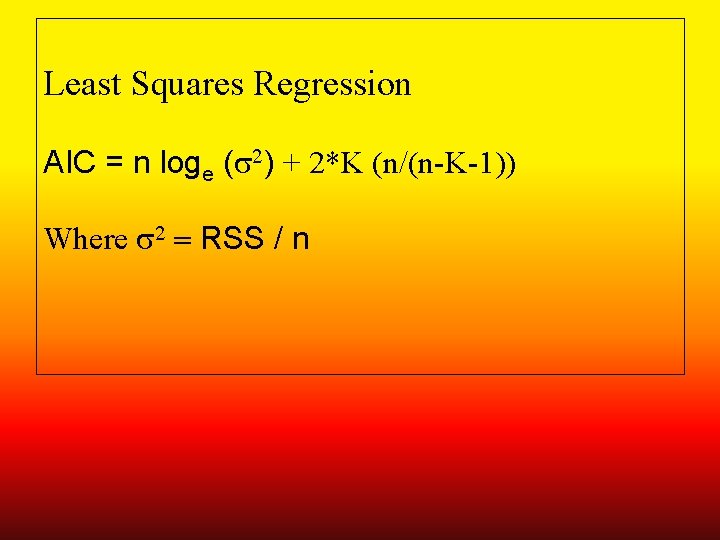
Least Squares Regression AIC = n loge (s 2) + 2*K (n/(n-K-1)) Where s 2 = RSS / n

Counting Parameters: K = number of parameters estimated Least Square Regression K = number of parameters + 2 (for intercept & s)

Counting Parameters: K = number of parameters estimated Logistic Regression K = number of parameters + 1 (for intercept)

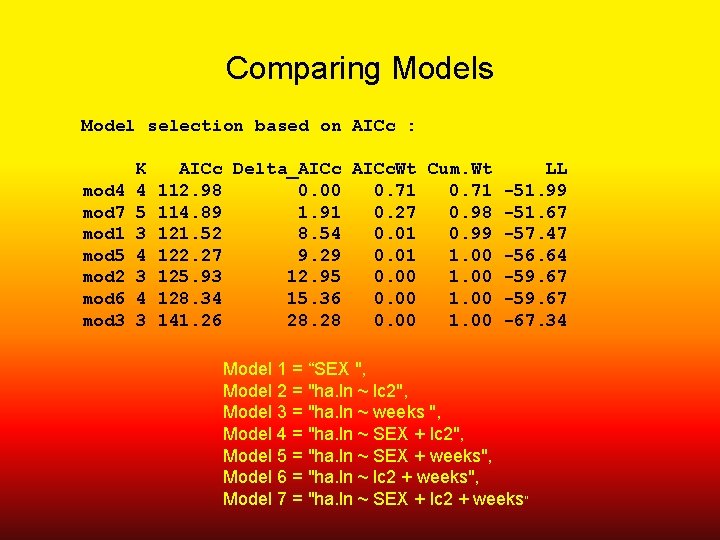
Comparing Models Model selection based on AICc : mod 4 mod 7 mod 1 mod 5 mod 2 mod 6 mod 3 K 4 5 3 4 3 AICc Delta_AICc. Wt Cum. Wt LL 112. 98 0. 00 0. 71 -51. 99 114. 89 1. 91 0. 27 0. 98 -51. 67 121. 52 8. 54 0. 01 0. 99 -57. 47 122. 27 9. 29 0. 01 1. 00 -56. 64 125. 93 12. 95 0. 00 1. 00 -59. 67 128. 34 15. 36 0. 00 1. 00 -59. 67 141. 26 28. 28 0. 00 1. 00 -67. 34 Model 1 = “SEX ", Model 2 = "ha. ln ~ lc 2", Model 3 = "ha. ln ~ weeks ", Model 4 = "ha. ln ~ SEX + lc 2", Model 5 = "ha. ln ~ SEX + weeks", Model 6 = "ha. ln ~ lc 2 + weeks", Model 7 = "ha. ln ~ SEX + lc 2 + weeks"

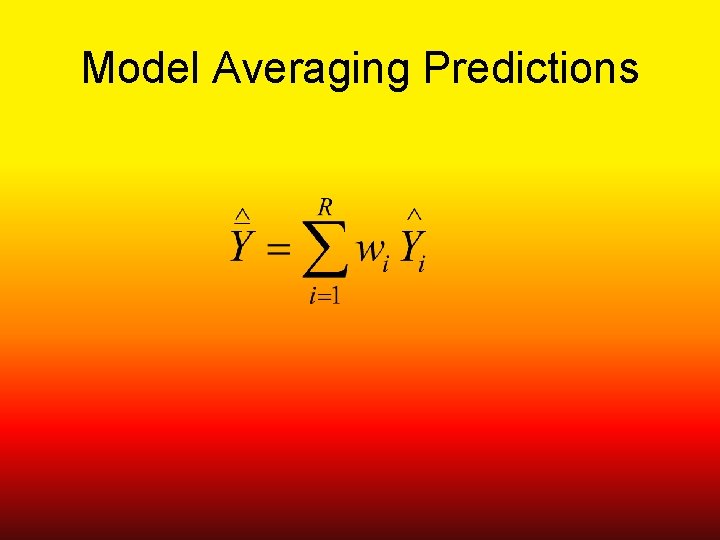
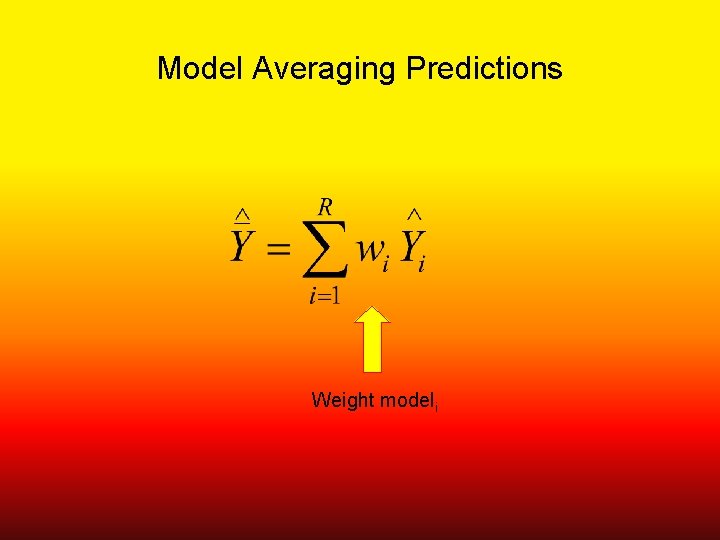
Model Averaging Predictions

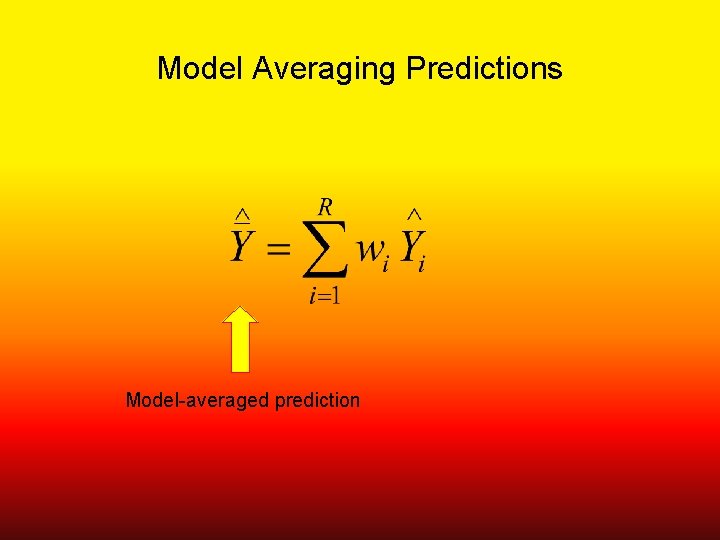
Model Averaging Predictions Model-averaged prediction

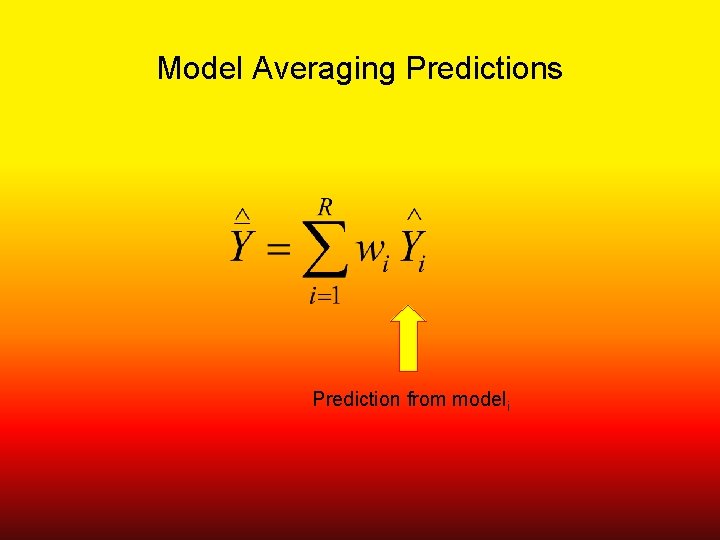
Model Averaging Predictions Prediction from modeli

Model Averaging Predictions Weight modeli

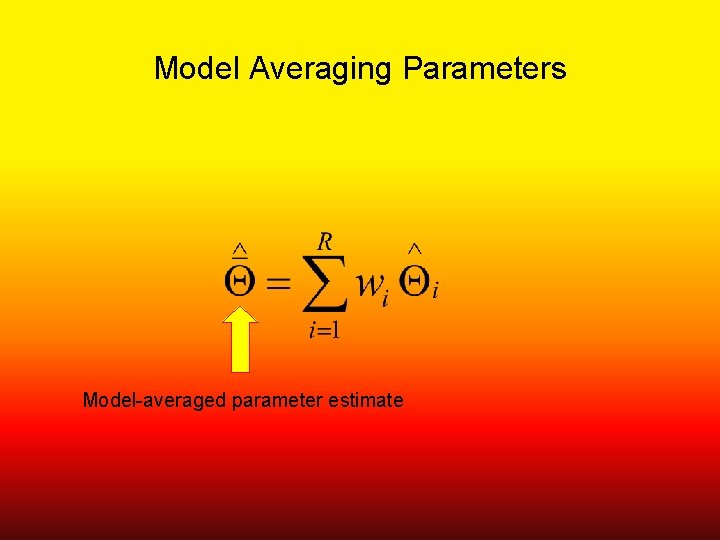
Model Averaging Parameters Model-averaged parameter estimate

Unconditional Variance Estimator

Unconditional Variance Estimator
