Potential Sweep Methods 2 25 2014 Linear Potential

Potential Sweep Methods 2 -25 -2014

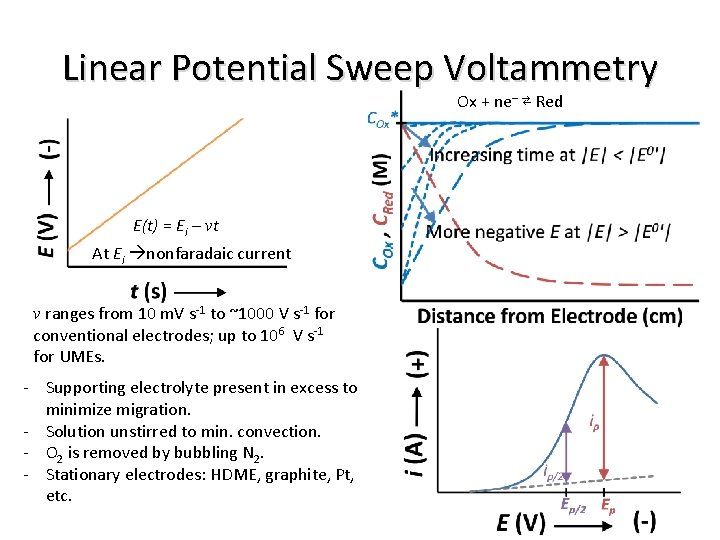
Linear Potential Sweep Voltammetry Ox + ne– ⇄ Red E(t) = Ei – vt At Ei nonfaradaic current v ranges from 10 m. V s-1 to ~1000 V s-1 for conventional electrodes; up to 106 V s-1 for UMEs. - Supporting electrolyte present in excess to minimize migration. - Solution unstirred to min. convection. - O 2 is removed by bubbling N 2. - Stationary electrodes: HDME, graphite, Pt, etc.

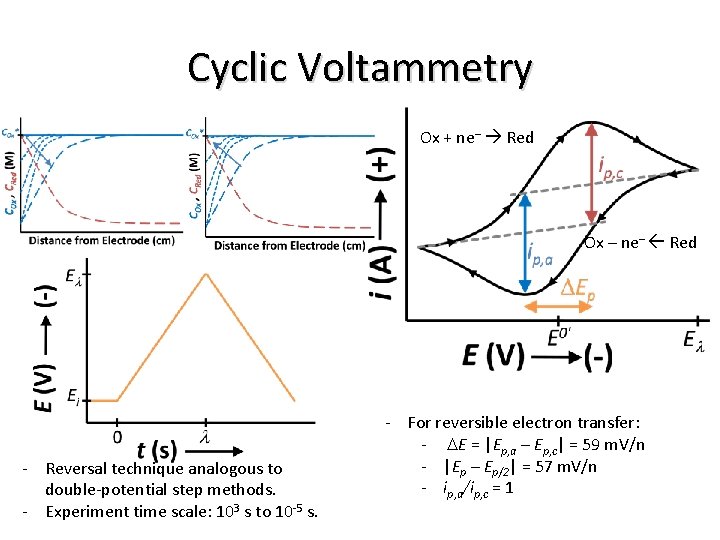
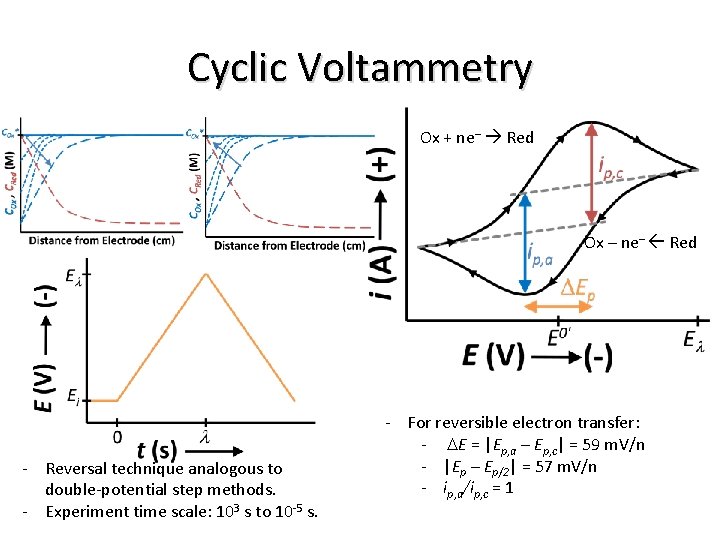
Cyclic Voltammetry Ox + ne– Red Ox – ne– Red - Reversal technique analogous to double-potential step methods. - Experiment time scale: 103 s to 10 -5 s. - For reversible electron transfer: - DE = |Ep, a – Ep, c| = 59 m. V/n - |Ep – Ep/2| = 57 m. V/n - ip, a/ip, c = 1

Derivation of i-E relationship: Description of system and conditions O + ne– ⇄ R (Assume semi-inf linear diff & only O initially present at potential Ei where no faradaic reaction occurs, rapid electron transfer) E(t) = Ei – vt CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] Time dependence makes Laplace transform complicated. Rewrite boundary condition (Nicholson & Shain): CO(0, t) / CR(0, t) = q e –st = q S(t) We want to determine the i-E relationship. Since E is linearly related to t, we first find the i-t relationship. Recall that current is proportional to flux at the electrode surface.

Review of i-t derivation strategy O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) Recall Fick’s 2 nd Law: CO(x, t) / t = DO 2 CO (x, t) / x 2 CR(x, t) / t = DR 2 CR(x, t) / x 2 CO(x, 0) = CO* CR(x, 0) = 0 limx CO(x, t) = CO* Recall Laplace Transform: L{ CO(x, t) / t} = L{DO 2 CO(x, t) / x 2} limx CR(x, t) = 0

Solving Laplace transform differential equation for concentration profile O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) To solve, consider the analogous equation: Find C(x) by inverse Laplace Notice D’ = b/a 2

Application of boundary conditions O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) CO(x, t) / t = DO 2 CO (x, t) / x 2 Recall Boundary conditions: CO(x, 0) = CO* CR(x, 0) = 0 limx CR(x, t) = 0 limx CO(x, t) = CO*

Determining coefficients for concentration profile O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) Flux balance: B’ = –A’x ; x = (DO/DR)(1/2) For any i-E experiment For reversible system (potential step): q = CO(0, t) / CR(0, t) = exp[n F (E – E 0’) / (R T)]

Current-time function for potential step O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For reversible system: q = CO(0, t) / CR(0, t) = exp[n F (E – E 0’) / (R T)] Consider Flux: x = (DO/DR)(1/2)

Concentration profile coefficients for potential sweep O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For reversible system (Potential Sweep): CO(0, t) / CR(0, t) = q e –st = q S(t) CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] q = exp[n F (E – E 0’) / (R T)] Consider Flux: s = n F v/ (R T)

Concentration-time function at electrode surface for potential sweep O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For Potential Sweep: Convolution integral:

Application of boundary conditions to general concentration integral equations for potential sweep O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For Potential Sweep: f(t) = i(t) / (n F A) General equations for potential sweep (electrode kinetics/boundary conditions not yet considered) For reversible system (Potential Sweep): CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] q = exp[n F (E – E 0’) / (R T)] CO(0, t) / CR(0, t) = q e –st = q S(t) s = n F v/ (R T)

Using boundary conditions to find i-t relationship (reversible systems) O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) f(t) = i(t) / (n F A) For reversible system (Potential Sweep): CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] CO(0, t) / CR(0, t) = q e –st = q S(t) q = exp[n F (E – E 0’) / (R T)] s = n F v/ (R T)

Using boundary conditions to find i-t relationship (reversible systems) O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For reversible system (Potential Sweep): CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] CO(0, t) / CR(0, t) = q e –st = q S(t) x = (DO/DR)(1/2) f(t) = i(t) / (n F A) Solution gives i(t) i(E). Closed-form solution cannot be obtained, must use numerical methods.

i(t) to i(E) (reversible systems) O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For reversible system (Potential Sweep): x = (DO/DR)(1/2) f(t) = i(t) / (n F A) s t = n F v t/(R T) = n F (Ei – E)/(RT) q = exp[n F (E – E 0’) / (R T)] Change from i(t) i(E). f(t) = g(st); z = st

i(E) in sweep experiments (reversible system) O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) For reversible system (Potential Sweep): x = (DO/DR)(1/2) q = exp[n F (E – E 0’) / (R T)] f(t) = i(t) / (n F A) f(t) = g(st); z = st i = n F A CO* (p DO s)1/2 c(s t) (6. 2. 17) s t = n F v t/(R T) = n F (Ei – E)/(RT) c(st) is a pure number for any given t.

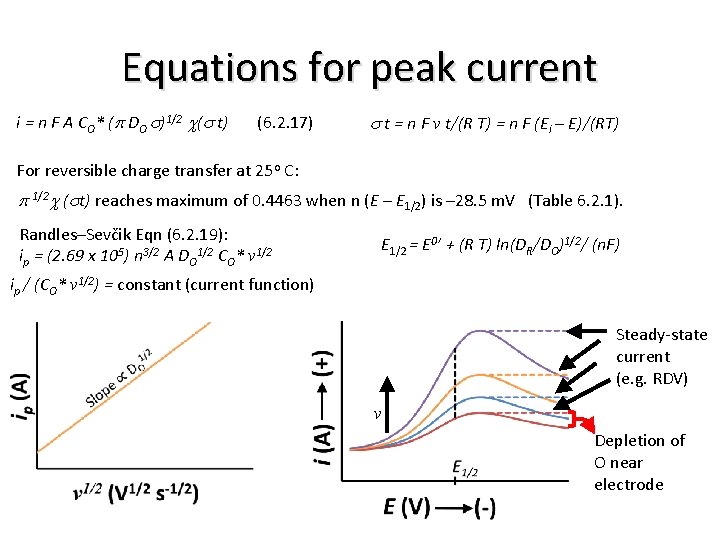
Equations for peak current i = n F A CO* (p DO s)1/2 c(s t) (6. 2. 17) s t = n F v t/(R T) = n F (Ei – E)/(RT) For reversible charge transfer at 25 o C: p 1/2 c (st) reaches maximum of 0. 4463 when n (E – E 1/2) is – 28. 5 m. V (Table 6. 2. 1). Randles–Sevčik Eqn (6. 2. 19): ip = (2. 69 x 105) n 3/2 A DO 1/2 CO* v 1/2 E 1/2 = E 0’ + (R T) ln(DR/DO)1/2/ (n. F) ip / (CO* v 1/2) = constant (current function) Steady-state current (e. g. RDV) v Depletion of O near electrode

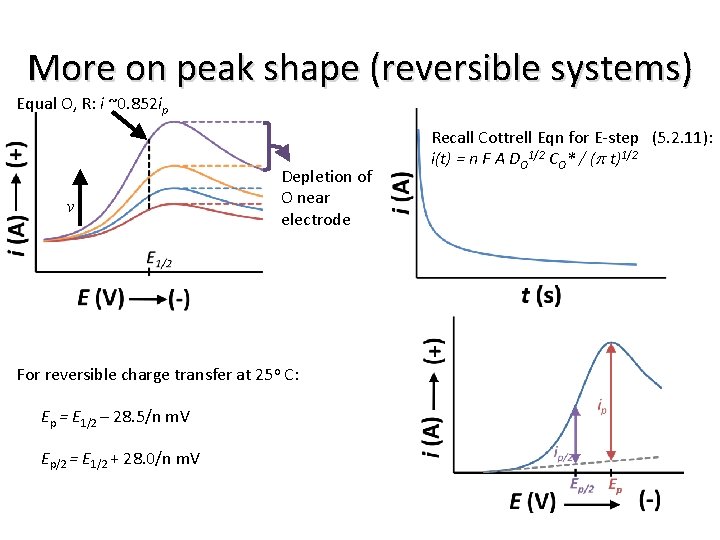
More on peak shape (reversible systems) Equal O, R: i ~0. 852 ip v Depletion of O near electrode For reversible charge transfer at 25 o C: Ep = E 1/2 – 28. 5/n m. V Ep/2 = E 1/2 + 28. 0/n m. V Recall Cottrell Eqn for E-step (5. 2. 11): i(t) = n F A DO 1/2 CO* / (p t)1/2

LSV with spherical electrodes and UMEs i = n F A CO* (p DO s)1/2 c(s t) + n F A DO CO* f(s t) / r 0 i (plane) i (spherical correction) s t = n F v t/(R T) = n F (Ei – E)/(RT) Spherical term dominates if v << R T D / (n F r 02) If 0. 5 mm radius, D = 10 -5 cm 2/s, T = 298 K, steady state up to 10 V/s. v

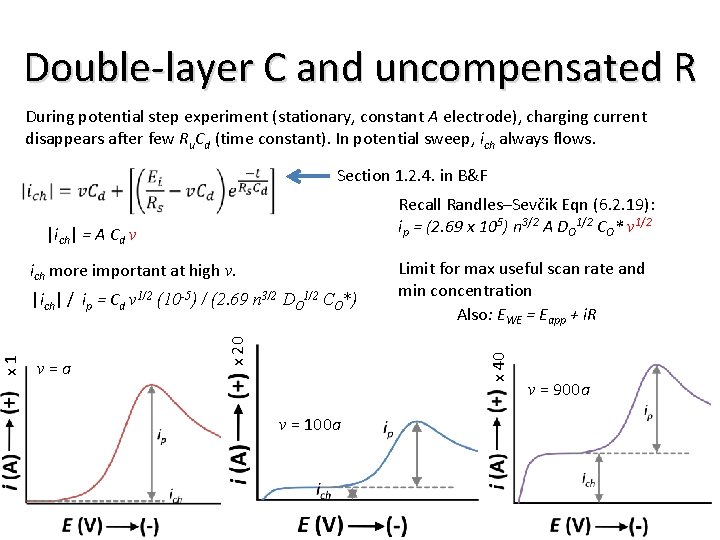
Double-layer C and uncompensated R During potential step experiment (stationary, constant A electrode), charging current disappears after few Ru. Cd (time constant). In potential sweep, ich always flows. Section 1. 2. 4. in B&F Recall Randles–Sevčik Eqn (6. 2. 19): ip = (2. 69 x 105) n 3/2 A DO 1/2 CO* v 1/2 |ich| = A Cd v ich more important at high v. |ich| / ip = Cd v 1/2 (10 -5) / (2. 69 n 3/2 DO 1/2 CO*) Limit for max useful scan rate and min concentration Also: EWE = Eapp + i. R x 40 v = a x 20 x 1 v = 100 a v = 900 a

Irreversible e– transfer (boundary condition) O + ne– ⇄ R (Assume semi-inf linear diff, only O initially present, and rapid charge-transfer kinetics) Recall boundary condition for reversible system (Potential Sweep): CO(0, t) / CR(0, t) = q e –st = q S(t) CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] And the general concentration equations: f(t) = i(t) / (n F A) Led to: i = n F A CO* (p DO s)1/2 c(s t) (6. 2. 17) kf – O + e R (Assume semi-inf linear diff, only O initially present, and totally irreversible, one -electron, one-step) The corresponding boundary condition is: Sec. 5. 5 in B&F

Irreversible e– transfer i(E) kf – O + e R (Assume semi-inf linear diff, only O initially present, and totally irreversible, one -electron, one-step) The corresponding boundary condition is: f = F / (R T) And the general concentration equations: f(t) = i(t) / (n F A) Leads to: i = F A CO* (p DO v)1/2 [(a F) / (R T)]1/2 c(bt) (6. 3. 6) Compare to Reversible: i = n F A CO* (p DO s)1/2 c(s t) (6. 2. 17) b=afv a transfer coefficient

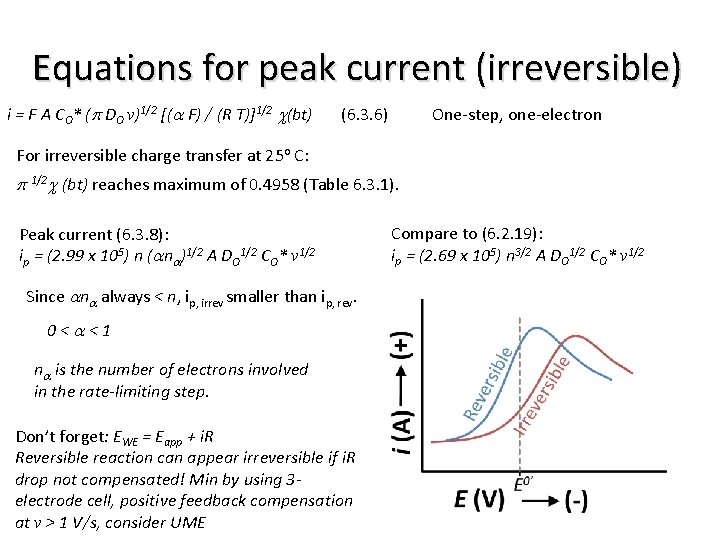
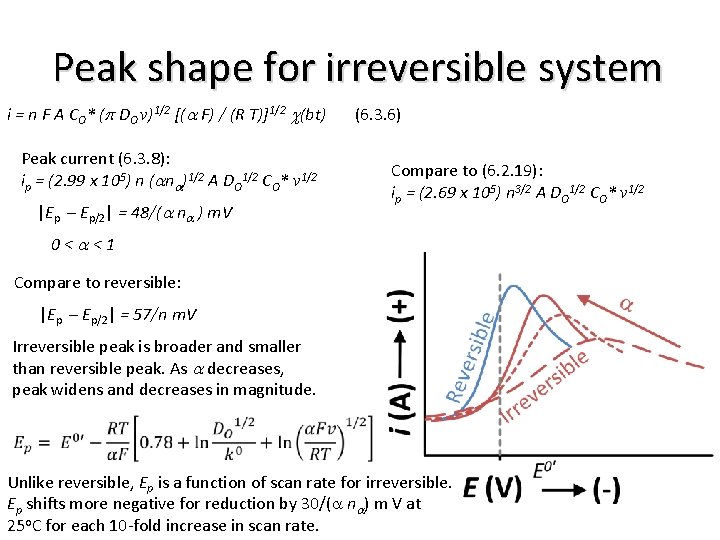
Equations for peak current (irreversible) i = F A CO* (p DO v)1/2 [(a F) / (R T)]1/2 c(bt) (6. 3. 6) One-step, one-electron For irreversible charge transfer at 25 o C: p 1/2 c (bt) reaches maximum of 0. 4958 (Table 6. 3. 1). Peak current (6. 3. 8): ip = (2. 99 x 105) n (ana)1/2 A DO 1/2 CO* v 1/2 Since ana always < n, ip, irrev smaller than ip, rev. 0<a<1 na is the number of electrons involved in the rate-limiting step. Don’t forget: EWE = Eapp + i. R Reversible reaction can appear irreversible if i. R drop not compensated! Min by using 3 electrode cell, positive feedback compensation at v > 1 V/s, consider UME Compare to (6. 2. 19): ip = (2. 69 x 105) n 3/2 A DO 1/2 CO* v 1/2

Peak shape for irreversible system i = n F A CO* (p DO v)1/2 [(a F) / (R T)]1/2 c(bt) (6. 3. 6) Peak current (6. 3. 8): ip = (2. 99 x 105) n (ana)1/2 A DO 1/2 CO* v 1/2 |Ep – Ep/2| = 48/(a na ) m. V Compare to (6. 2. 19): ip = (2. 69 x 105) n 3/2 A DO 1/2 CO* v 1/2 0<a<1 Compare to reversible: |Ep – Ep/2| = 57/n m. V Irreversible peak is broader and smaller than reversible peak. As a decreases, peak widens and decreases in magnitude. Unlike reversible, Ep is a function of scan rate for irreversible. Ep shifts more negative for reduction by 30/(a na) m V at 25 o. C for each 10 -fold increase in scan rate.

Quasireversible e– transfer (boundary condition) Recall boundary condition and i(E) relationship for reversible system (Potential Sweep): CO(0, t) / CR(0, t) = q e –st = q S(t) CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] i = n F A CO* (p DO s)1/2 c(s t) (6. 2. 17) And the boundary condition and i(E) relationship for the totally irreversible system: i = F A CO* (p DO v)1/2 [(a F) / (R T)]1/2 c(bt) (6. 3. 6) f = F / (R T) Now consider reactions where electron transfer limitations make consideration of the reverse reaction necessary (quasireversible – Matsuda and Ayabe): kf – (Assume semi-inf linear diff, only O initially present, one-electron, one-step) O + e ⇄ R The corresponding boundary condition is: kb

Quasireversible e– transfer equations Now consider reactions where electron transfer limitations make consideration of the reverse reaction necessary (quasireversible – Matsuda and Ayabe): kf – (Assume semi-inf linear diff, only O initially present, one-electron, one-step) O + e ⇄ R kb The corresponding boundary condition is: Matsuda and Ayabe showed peak shape and characteristics to be function of a and parameter L: i = F A CO* (DO v)1/2 [F/ (R T)]1/2 Y(E) (6. 4. 5)

Quasireversible, irreversible Now consider reactions where electron transfer limitations make consideration of the reverse reaction necessary (quasireversible – Matsuda and Ayabe): kf O + e– ⇄ R kb Matsuda and Ayabe showed peak shape and characteristics to be function of a and parameter L: i = F A CO* (DO v)1/2 [F/ (R T)]1/2 Y(E) (6. 4. 5) i = n F A CO* (p DO s)1/2 c(s t) (6. 2. 17) i = F A CO* (p DO v)1/2 [(a F) / (R T)]1/2 c(bt) (6. 3. 6) Y(E) is shown in Fig. 6. 4. 1. L > 10, behavior of Y(E) approaches that of reversible system. System |Ep – Ep/2|at 25 o. C (m. V) Reversible 57/n Irreversible 48/(a na ) Quasireversible 26 D(L, a) L ≥ 10, D(L, a) ≈ 2. 2 |Ep – Ep/2| ≈ 57 L < 10 -2 & a = 0. 5, D(L, a) ≈ 3. 7 |Ep – Ep/2| ≈ 96

Scan rate and kinetics System |Ep – Ep/2|at 25 o. C (m. V) Reversible 57/n Irreversible 48/(a na ) Quasireversible 26 D(L, a) L ≥ 10, D(L, a) ≈ 2. 2 |Ep – Ep/2| ≈ 57 L < 10 -2 & a = 0. 5, D(L, a) ≈ 3. 7 |Ep – Ep/2| ≈ 96 Depending on L (v), a system may show rev, quasirev or irrev behavior. Appearance of kinetic effects depends on time window of experiment. At small v (long t) rev, while at large v (short t) irrev. For n = 1, a = 0. 5, T = 25 o. C, and D = 10 -5 cm 2/s with L ≈ k 0/(39 D v)1/2 Matsuda and Ayabe suggested Reversible: L ≥ 15 ; k 0 ≥ 0. 3 v 1/2 cm/s Quasireversible: 15 ≥ L ≥ 10 – 2(1+a) ; 0. 3 v 1/2 cm/s ≥ k 0 ≥ 2 x 10 -5 v 1/2 cm/s Totally irreversible: L ≤ 10 – 2(1+a) ; k 0 ≤ 2 x 10 -5 v 1/2 cm/s Increased v makes rxn more difficult (broader wave, shifted negatively for reduction) Also need fast recorder < 0. 5 V s-1 ; computer or oscilloscope > 0. 5 V s-1 i. R compensation as i. R drop distorts linear input ramp of potential sweep EWE = Eapp + i. R

Cyclic Voltammetry Ox + ne– Red Ox – ne– Red - Reversal technique analogous to double-potential step methods. - Experiment time scale: 103 s to 10 -5 s. - For reversible electron transfer: - DE = |Ep, a – Ep, c| = 59 m. V/n - |Ep – Ep/2| = 57 m. V/n - ip, a/ip, c = 1

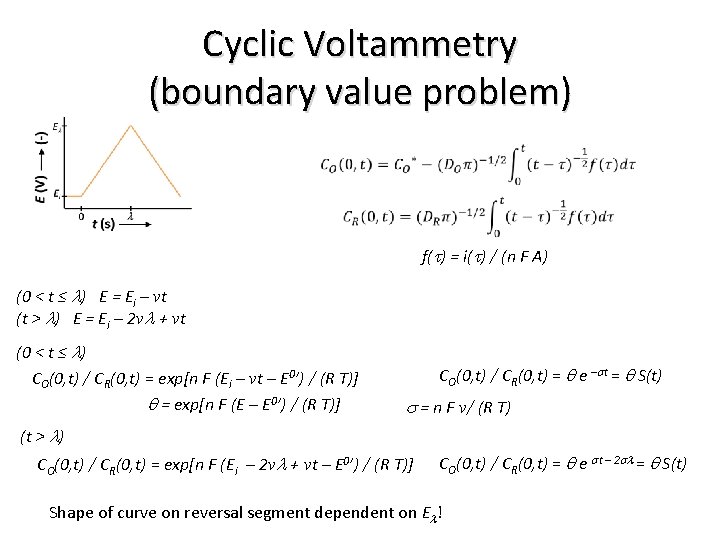
Cyclic Voltammetry (boundary value problem) f(t) = i(t) / (n F A) (0 < t ≤ l) E = Ei – vt (t > l) E = Ei – 2 vl + vt (0 < t ≤ l) CO(0, t) / CR(0, t) = exp[n F (Ei – vt – E 0’) / (R T)] q = exp[n F (E – E 0’) / (R T)] CO(0, t) / CR(0, t) = q e –st = q S(t) s = n F v/ (R T) (t > l) CO(0, t) / CR(0, t) = exp[n F (Ei – 2 vl + vt – E 0’) / (R T)] CO(0, t) / CR(0, t) = q e st – 2 sl = q S(t) Shape of curve on reversal segment dependent on El!

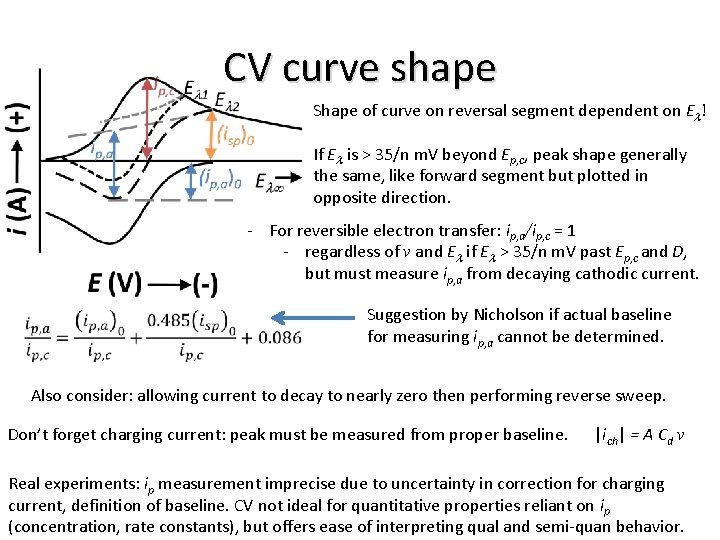
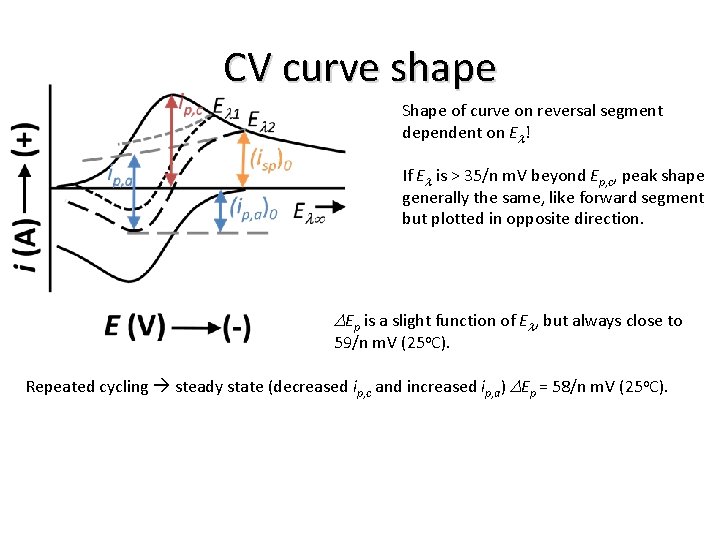
CV curve shape Shape of curve on reversal segment dependent on El! If El is > 35/n m. V beyond Ep, c, peak shape generally the same, like forward segment but plotted in opposite direction. - For reversible electron transfer: ip, a/ip, c = 1 - regardless of v and El if El > 35/n m. V past Ep, c and D, but must measure ip, a from decaying cathodic current. Suggestion by Nicholson if actual baseline for measuring ip, a cannot be determined. Also consider: allowing current to decay to nearly zero then performing reverse sweep. Don’t forget charging current: peak must be measured from proper baseline. |ich| = A Cd v Real experiments: ip measurement imprecise due to uncertainty in correction for charging current, definition of baseline. CV not ideal for quantitative properties reliant on ip (concentration, rate constants), but offers ease of interpreting qual and semi-quan behavior.

CV curve shape Shape of curve on reversal segment dependent on El! If El is > 35/n m. V beyond Ep, c, peak shape generally the same, like forward segment but plotted in opposite direction. DEp is a slight function of El, but always close to 59/n m. V (25 o. C). Repeated cycling steady state (decreased ip, c and increased ip, a) DEp = 58/n m. V (25 o. C).

CV curve shape (quasirev) Recall for quasirev: y (at 25 o. C) DEp (m. V) 20 61 5 65 2 72 0. 5 105 0. 25 141 DEp is a function of v, k 0, a, and El. If El is 90/n m. V beyond peak, El effect is small. 0. 3 < a < 0. 7, DEp nearly ind of a, only depends on y (Nicholson method) Variation of DEp with v y estimate k 0 Beware of uncomp R: ip. Ru must be small. Effect of Ru most important when currents large and k 0 rev limit (DEp only slightly diff from rev value)

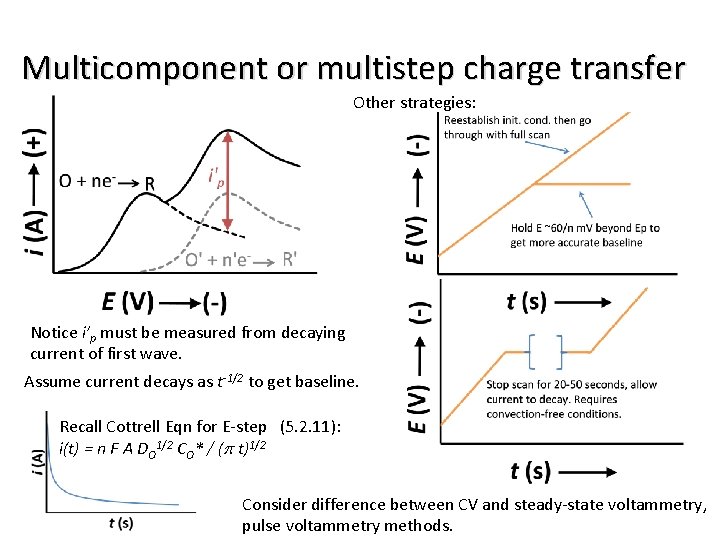
Multicomponent or multistep charge transfer Other strategies: Notice i’p must be measured from decaying current of first wave. Assume current decays as t-1/2 to get baseline. Recall Cottrell Eqn for E-step (5. 2. 11): i(t) = n F A DO 1/2 CO* / (p t)1/2 Consider difference between CV and steady-state voltammetry, pulse voltammetry methods.

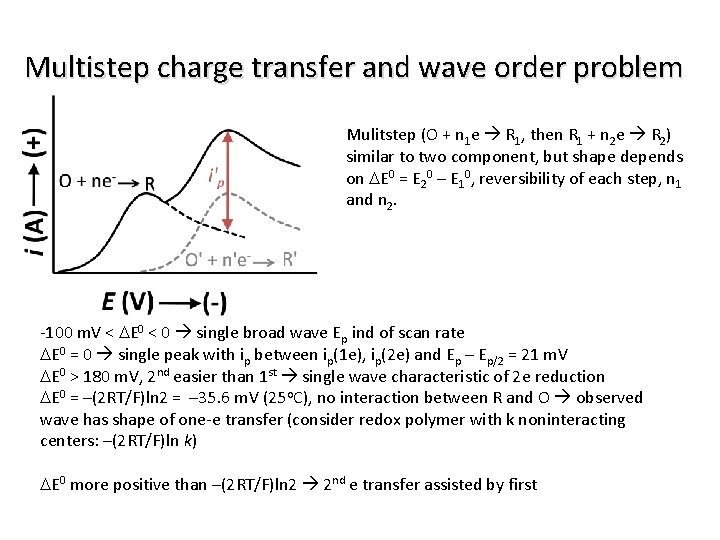
Multistep charge transfer and wave order problem Mulitstep (O + n 1 e R 1, then R 1 + n 2 e R 2) similar to two component, but shape depends on DE 0 = E 20 – E 10, reversibility of each step, n 1 and n 2. -100 m. V < DE 0 < 0 single broad wave Ep ind of scan rate DE 0 = 0 single peak with ip between ip(1 e), ip(2 e) and Ep – Ep/2 = 21 m. V DE 0 > 180 m. V, 2 nd easier than 1 st single wave characteristic of 2 e reduction DE 0 = –(2 RT/F)ln 2 = – 35. 6 m. V (25 o. C), no interaction between R and O observed wave has shape of one-e transfer (consider redox polymer with k noninteracting centers: –(2 RT/F)ln k) DE 0 more positive than –(2 RT/F)ln 2 2 nd e transfer assisted by first

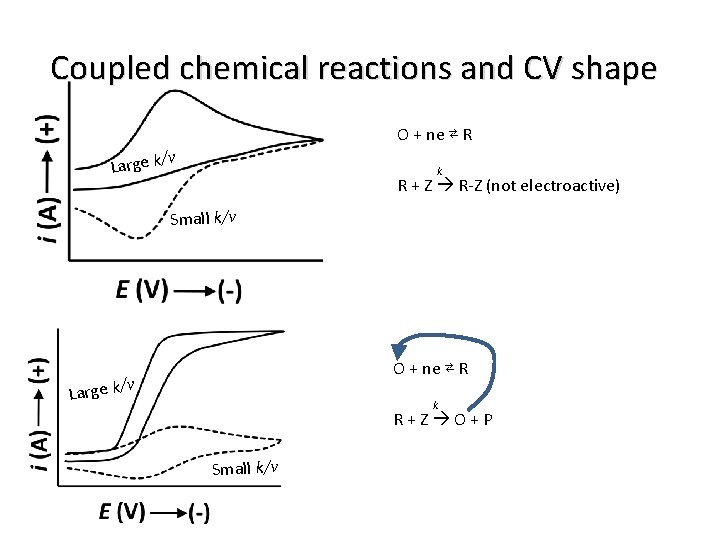
Coupled chemical reactions and CV shape O + ne ⇄ R /v Large k k R + Z R-Z (not electroactive) Small k/v O + ne ⇄ R /v Large k k R + Z O + P Small k/v

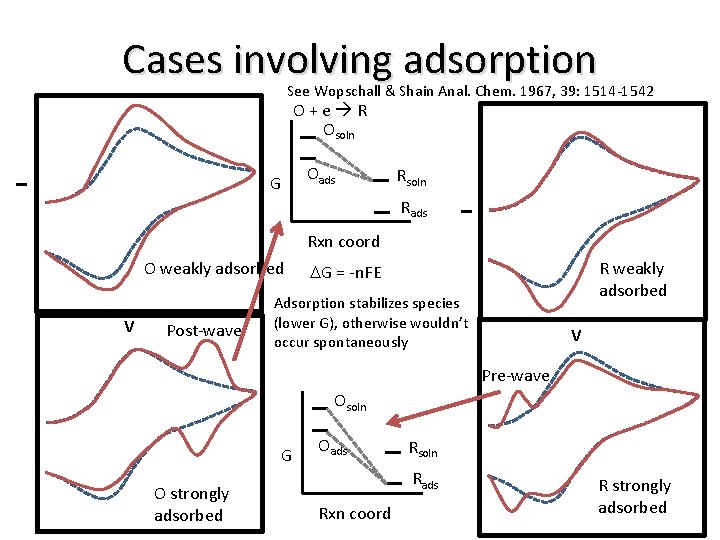
Cases involving adsorption See Wopschall & Shain Anal. Chem. 1967, 39: 1514 -1542 O + e R Osoln I Rsoln Rads I Oads G Rxn coord O weakly adsorbed V Post-wave R weakly adsorbed DG = -n. FE Adsorption stabilizes species (lower G), otherwise wouldn’t occur spontaneously V Pre-wave Osoln G O strongly adsorbed Oads Rsoln Rads Rxn coord R strongly adsorbed

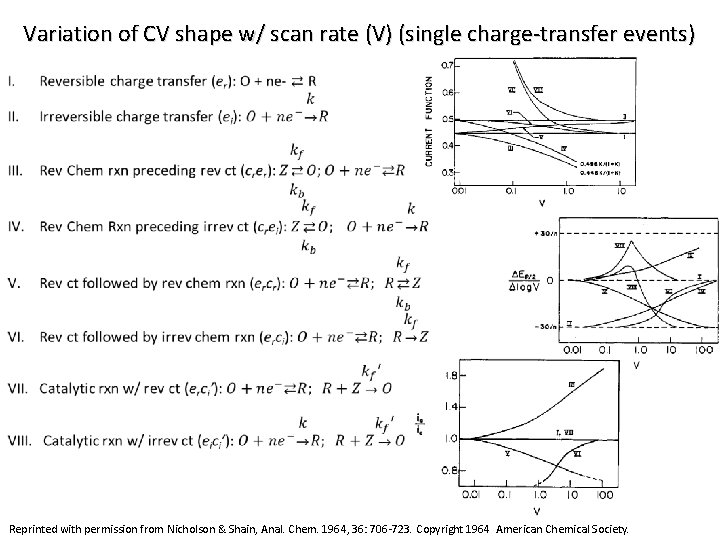
Variation of CV shape w/ scan rate (V) (single charge-transfer events) Reprinted with permission from Nicholson & Shain, Anal. Chem. 1964, 36: 706 -723. Copyright 1964 American Chemical Society.

Linear sweep methods • Signal shape can depend on electrode size, v, k 0, a, El • Good for qualitative or semi-quantitative description of system based on ip, DEp • Experimental data compared to mathematical models • ip measurement complicated by baseline correction – ich, i. R drop, reversal baseline – mathematical corrections, additional experiments • High scan rates: quasireversible behavior, large i. R effect • Detection limit ~10 -6 or 10 -7 M at best