Measurement Linear Agriculture Mechanics I Linear Measurements Linear

Measurement- Linear Agriculture Mechanics I

Linear Measurements � Linear ◦ Comes from the word line. � Linear Measure ◦ The measurement of lines ◦ A line is the distance between two points. ◦ It is one-dimensional (having length but no width or thickness). ◦ The lines to be measured can be curved, irregular, or straight.

Finding “Perimeters” � Perimeter- is the distance around the outside of an area or an object. � For Example, the boundaries of Tulare High School form its perimeter.

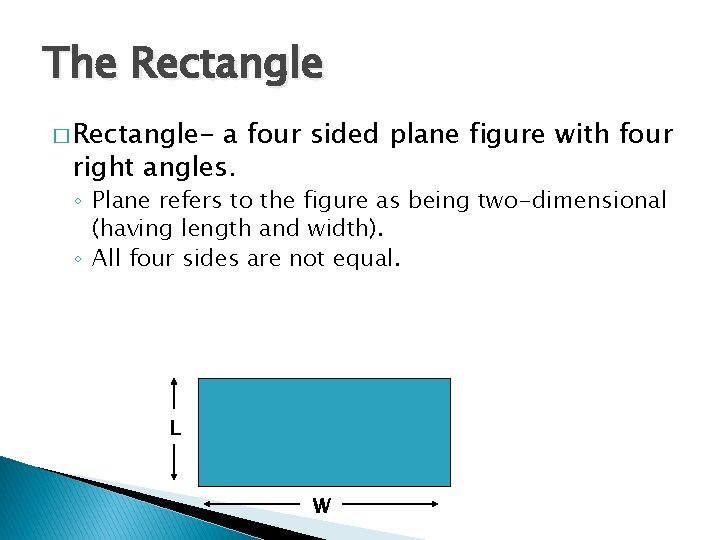
The Rectangle � Rectangle- a four sided plane figure with four right angles. ◦ Plane refers to the figure as being two-dimensional (having length and width). ◦ All four sides are not equal. L W

Finding the Perimeter of a Rectangle � There is a long and a short method ◦ Long method- add up the lengths of all sides. �P = L + W + L + W ◦ Short method- uses a formula �P = 2 L + 2 W (2 x length + 2 x width) � Example: ◦ ◦ L = 10 W=5 P = 2(10) + 2(5) P = 30 10 5

The Square � Square- is a plane figure with four equal sides and four right angles. � The formula for finding the perimeter of a square is P = 4 s ◦ The letter “s” stands for the length of one side. � Example: Find the perimeter of a hog pen whose sides are 15 feet. ◦P=4 s ◦ P = 4 (15) ◦ P = 60 feet 15’

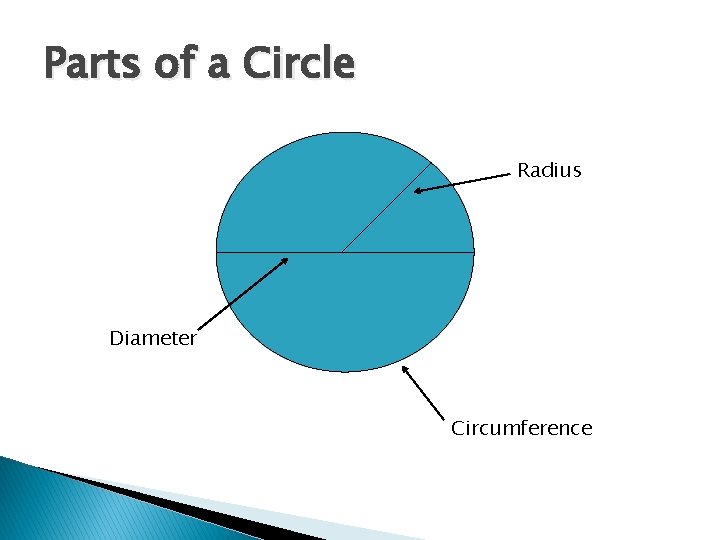
Finding the Circumference of Circles � Circle- a closed plane curve, every point of which is equally distant from a center point. � The circumference is the perimeter around the circle. � The diameter is the distance across the circle, through the center. � The radius is half of the diameter (from the center to the circle line).

Parts of a Circle Radius Diameter Circumference

Formulas of Circles � The formulas used for finding the circumference, diameter, and radius are derived from the relationship that exists between any circle’s circumference and diameter. ◦ This relationship is referred to as the RATIO of the circumference to the diameter. �Circumference/Diameter = 3. 14 (rounded off) ◦ The number 3. 14 has been named with the Greek letter π (pi) ◦C/d=π

Formulas of Circles cont. � To find a circle’s circumference, the following formulas can be used: ◦ C = π x diameter or C=πd ◦ C = 2 x π x radius or C=2πr � Example: Find the circumference of a grain silo when the diameter is 25’ d = 25’ C=πxd π = 3. 14 C = 3. 14 x 25 C=? C = 78. 5’

Formulas of Circles cont. � To find a circle’s diameter, the following formulas can be used: ◦ d=C/π ◦ d = 2 r � Example: Find the diameter of a stock tank when the circumference is 30’ ? C = 30 d=C/π π = 3. 14 d = 30 / 3. 14 d=? d = 9. 55’