Poetry The Pumping Lemma Any regular language L






















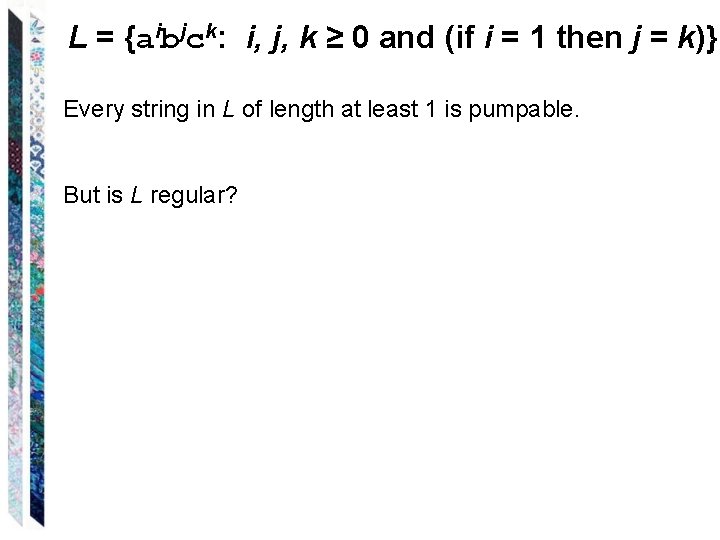



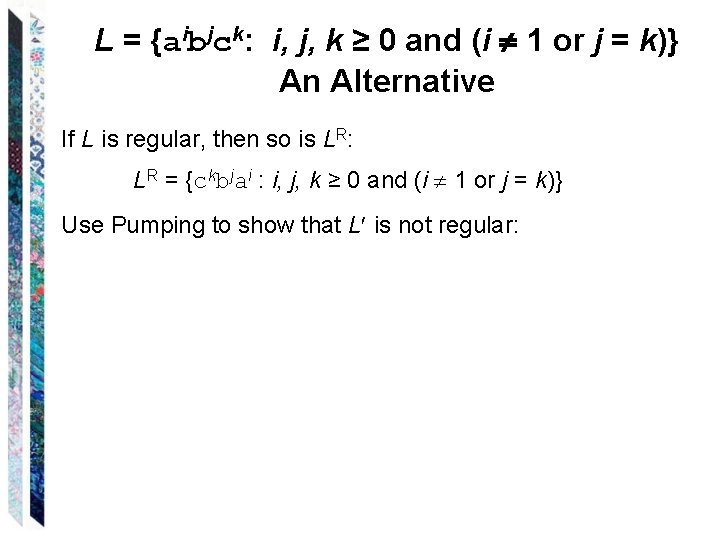








- Slides: 36

Poetry The Pumping Lemma Any regular language L has a magic number p And any long-enough word in L has the following property: Amongst its first p symbols is a segment you can find Whose repetition or omission leaves x amongst its kind. So if you find a language L which fails this acid test, And some long word you pump becomes distinct from all the rest, By contradiction you have shown that language L is not A regular guy, resiliant to the damage you have wrought. But if, upon the other hand, x stays within its L, Then either L is regular, or else you chose not well. For w is xyz, and y cannot be null, And y must come before p symbols have been read in full. As mathematical postscript, an addendum to the wise: The basic proof we outlined here does certainly generalize. So there is a pumping lemma for all languages context-free, Although we do not have the same for those that are r. e. -- Martin Cohn

MA/CSSE 474 Theory of Computation More on showing L non-regular (Pumping Theorem Examples)

Your Questions? • Previous class days' material (especially the Pumping Theorem) • Reading Assignments • HW 7 problems • Why Problem 10 on HW 6? • Anything else 474 difficulty level vs time

Using The Pumping Theorem to show that L is not Regular: We use the contrapositive of theorem: If some long enough string in L is not "pumpable", then L is not regular. What we need to show in order to show L non-regular: ( k 1 ( a string w L (|w| k and ( x, y, z ((w = xyz ∧ |xy| k ∧ y ) → q 0 (xyqz ∉ L)))))) → L is not regular. Soon: Be sure that you are convinced that this really is the contrapositive of the pumping theorem.

A way to think of it: adversary argument (following J. E. Hopcroft and J. D. Ullman) 1. Choose the language L you want to prove non-regular. 2. The "adversary" picks k, the constant mentioned in theorem. We must be prepared for any positive integer to be picked, but once it is chosen, the adversary cannot change it. 3. We select a string w L (whose length is at least k) that cannot be "pumped". 4. The adversary breaks w into w=xyz, subject to the constraints |xy| k and y . Our choice of w must take into account that any such x and y can be chosen. 5. All we must do is produce a single number q 0 such that xyqz L. Note carefully what we get to choose and what we do not get to choose.

Example: {anbn: n 0} is not Regular k is the number from the Pumping Theorem. We don't get to choose it. Choose w to be a k/2 b k/2 (“long enough”). 1 2 aaaaa…aaaaabbbb …bbbbbb x y z Adversary chooses x, y, z with the required properties: |xy| k, For each case, we must y , find at least one value of q We must show ∃ q 0 (xy z ∉ L). q Three cases to consider: ● y entirely in region 1: ●y partly in region 1, partly in 2: ●y entirely in region 2: q that takes xy z outside the language L. The most common q values to use are q=0 and q=2.

A Complete Proof We prove that L = {anbn: n 0} is not regular If L were regular, then there would exist some k such that any string w where |w| k must satisfy the conditions of theorem. Let w = a k/2 b k/2. Since |w| k, w must satisfy the conditions of the pumping theorem. So, for some x, y, and z, w = xyz, |xy| k, y , and q 0, xyqz is in L. We show that no such x, y, and z exist. There are 3 cases for where y could occur: We divide w into two regions: aaaaa…. . aaaaaa 1 | bbbbb…. . bbbbbb | 2 So y can fall into: ● (1): y = ap for some p. Since y , p must be greater than 0. Let q = 2. The resulting string is a k/2 +pb k/2. But this string is not in L, since it has more a’s than b’s. ● (2): y = bp for some p. Since y , p must be greater than 0. Let q = 2. The resulting string is a k/2 b k/2 +p. But this string is not in L, since it has more b’s than a’s. It would also be okay to simply write "same as previous case" ● (1, 2): y = apbr for some non-zero p and r. Let q = 2. The resulting string will contain interleaved a’s and b’s, and so is not in L. There exists one long string in L for which no "always pumpable" x, y, and z exist. So L is not regular.

What You Should Write (read these details later) We prove that L = {anbn: n 0} is not regular Let w = a k/2 b k/2. (If not completely obvious, as it is in this case, show that w is in fact in L. ) aaaaa…. . aaaaaa| bbbbb…. . bbbbbb 1 | 2 There are three possibilities for y: ● (1): y = ap for some p. Since y , p must be greater than 0. Let q = 2. The resulting string is a k/2 +pb k/2. But this string is not in L, since it has more a’s than b’s. ● (2): y = bp for some p. Since y , p must be greater than 0. Let q = 2. The resulting string is a k/2 b k/2 +p. But this string is not in L, since it has more b’s than a’s. It would also be okay to simply write "same as previous case" ● (1, 2): y = apbr for some non-zero p and r. Let q = 2. The resulting string will contain interleaved a’s and b’s, and so is not in L. Thus L is not regular.

Using the Pumping Theorem Effectively ● To choose w: ● Choose a w that is in the part of L that makes it not regular. ● Choose a w that is only barely in L. ● Choose a w with as homogeneous as possible an initial region of length at least k. ● To choose q: ● Try letting q be either 0 or 2. ● If that doesn’t work, analyze L to see if there is some other specific value that will work.

A better choice for w Second try. A choice of w that makes it easier: Choose w to be akbk (We get to choose any w whose length is at least k). 1 2 aaaaa…aaaaabbbb …bbbbbb x y z We show that there is no x, y, z with the required properties: |xy| k, y , q 0 (xyqz is in L). Since |xy| k, y must be in region 1. So y = ap for some p 1. Let q = 2, producing: ak+pbk which L, since it has more a’s than b’s. We only have to find one q that takes us outside of L.

Recap: Using the Pumping Theorem If L is regular, then every “long” string in L is pumpable. To show that L is not regular, for every length k, we find one long string (k chars or longer) that isn’t pumpable. 1. Choose a string w where |w| k. Since we do not know what k is, we must describe w in terms of k. 2. Divide the possibilities for y into a set of equivalence classes that can be considered together. 3. For each such class of possible y values where |xy| k and y : Find a value for q such that xyqz is not in L. Our textbook uses the terms pump in for q>1, and pump out for q=0.

Examples: Use the Pumping Theorem to show that these languages are non-regular Bal = {w { ), ( }* : the parens are balanced} Pal. Even = {ww. R : w {a, b}*} {anbm: n m}

{abanbn : n 0} Choose w = abakbk k abaaaaabbbbbb x y z What are the choices for (x, y)? ( , a) ( , aba+) (a, ba+) (ab, a+) (aba*, a+)

A Different Approach to abanbn? Can we argue as follows: We already know that {anbn: n 0} is not regular. So neither is L. Can we defend this argument by appeal to the fact that the regular languages are closed under concatenation: L = ab ? regular || {anbn: n 0} not regular

L = {an: n is prime} L = {w = an: n is prime} Let w = aj, where j = smallest prime integer that is greater than k+1: a a a a x y z |x| + |z| is prime. |x| + |y| + |z| is prime. |x| + 2|y| + |z| is prime. |x| + 3|y| + |z| is prime, and so forth. | | | | | | | | | | | | | p But the Prime Number Theorem tells us that the primes "spread out", i. e. , that the number of primes not exceeding x is asymptotic to x/ln x.

L = {an: n is prime} Let k be any integer > 0. Choose w = aj, where j is the smallest prime number > k+1. y = ap for some p (p is not necessarily a prime number). If L is regular, q 0 (a|x| + |z| +q|y| must be in L). So |x| + |z| +q |y| must be prime Choose q = |x| + |z|. Then: |x| + |z| +q |y| = |x| + |z| + (|x| + |z|) |y| = (|x| + |z|) (1 + |y|), which is non-prime if both factors are greater than 1: (|x| + |z|) > 1 because |w| > k+1 and |y| k. (1 + |y|) > 1 because |y| > 0.

Using the Pumping Theorem Effectively ● To choose w: ● Choose a w that is in the part of L that makes it not regular. ● Choose a w that is only barely in L. ● Choose a w with as homogeneous as possible an initial region of length at least k. ● To choose q: ● Try letting q be either 0 or 2. ● If that doesn’t work, analyze L to see if there is some other specific value that will work.

Using the Closure Properties The two most useful properties are closure under: • Intersection • Complement

Using the Closure Properties L = {w {a, b}*: #a(w) = #b(w)} If L were regular, then: L = L _______ would also be regular. But it isn’t.

L = {aibj: i, j 0 and i j} Try to use the Pumping Theorem by letting w = akbk+k!. Then y = ap for some nonzero p. Let q = (k!/p) + 1 (i. e. , pump in (k!/p) times). Note that (k!/p) must be an integer because p < k. The number of a’s in the new string is k + (k!/p)p = k + k!. So the new string is ak+k!bk+k!, which has equal numbers of a’s and b’s and so is not in L.

L = {aibj: i, j 0 and i j} An easier way: If L is regular then so is L. Is it?

L = {aibj: i, j 0 and i j} An easier way: If L is regular then so is L. Is it? L = An. Bn {out of order} If L is regular, then so is L = L a*b* = ______

The rest of today's slides • I doubt that we will get to many of them • They are here as examples in case they are helpful for you as you do HW 7 • Tomorrow we may do some of these examples in class, but not all of them • Most of them are discussed in detail in the textbook
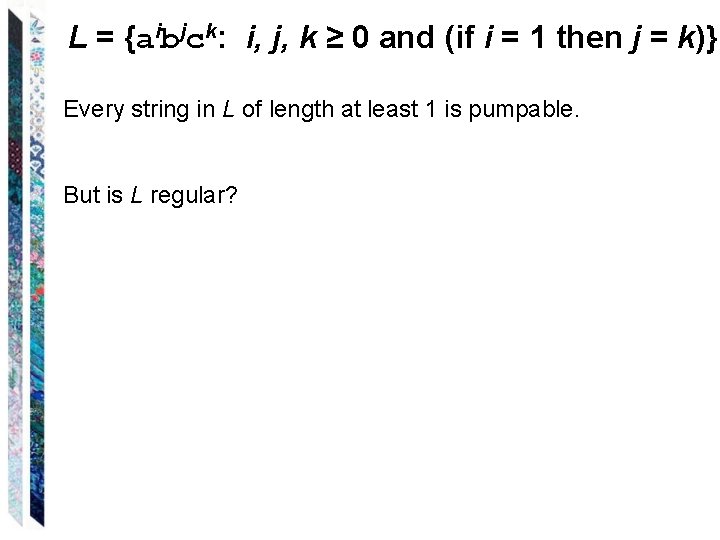
L = {aibjck: i, j, k ≥ 0 and (if i = 1 then j = k)} Every string in L of length at least 1 is pumpable. But is L regular?

L = {aibjck: i, j, k ≥ 0 and (if i = 1 then j = k)} Every string in L of length at least 1 is pumpable. Rewrite the final condition as: (i 1) or (j = k)

L = {aibjck: i, j, k ≥ 0 and (i 1 or j = k)} Every string in L of length at least 1 is pumpable: • If i = 0 then: if j 0, let y be b; otherwise, let y be c. Pump in or out. Then i will still be 0 and thus not equal to 1, so the resulting string is in L. • If i = 1 then: let y be a. Pump in or out. Then i will no longer equal 1, so the resulting string is in L. • • If i = 2 then: let y be aa. Pump in or out. Then i cannot equal 1, so the resulting string is in L. • If i > 2 then: let y = a. Pump out once or in any number of times. Then i cannot equal 1, so the resulting string is in L.

L = {aibjck: i, j, k ≥ 0 and (i 1 or j = k)} But the closure theorems help. Suppose we guarantee that i = 1. If L is regular, then so is: L = L ab*c*. L = {abjck : j, k ≥ 0 and j = k} Use Pumping to show that L is not regular:
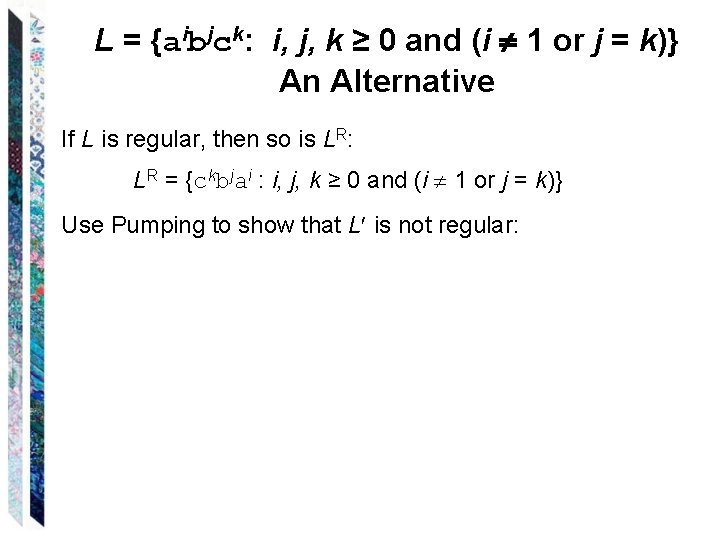
L = {aibjck: i, j, k ≥ 0 and (i 1 or j = k)} An Alternative If L is regular, then so is LR: LR = {ckbjai : i, j, k ≥ 0 and (i 1 or j = k)} Use Pumping to show that L is not regular:

Exploiting Problem-Specific Knowledge L = {w {0, 1, 2, 3, 4 , 5, 6, 7}*: w is the octal representation of a nonnegative integer that is divisible by 7}

Is English Regular? Is English finite?

In the event that the Purchaser defaults in the payment of any installment of purchase price, taxes, insurance, interest, or the annual charge described elsewherein, or shall default in the performance of any other obligations set forth in this Contract, the Seller may: at his option: (a) Declare immediately due and payable the entire unpaid balance of purchase price, with accrued interest, taxes, and annual charge, and demand full payment thereof, and enforce conveyance of the land by termination of the contract or according to the terms hereof, in which case the Purchaser shall also be liable to the Seller for reasonable attorney's fees for services rendered by any attorney on behalf of the Seller, or (b) sell said land premises or any part thereof at public auction, in such manner, at such time and place, upon such terms and conditions, and upon such public notice as the Seller may deem best for the interest of all concerned, consisting of advertisement in a newspaper of general circulation in the county or city in which the security property is located at least once a week for Three (3) successive weeks or for such period as applicable law may require and, in case of default of any purchaser, to re-sell with such postponement of sale or resale and upon such public notice thereof as the Seller may determine, and upon compliance by the Purchaser with the terms of sale, and upon judicial approval as may be required by law, convey said land premises in fee simple to and at the cost of the Purchaser, who shall not be liable to see to the application of the purchase money; and from the proceeds of the sale: First to pay all proper costs and charges, including but not limited to court costs, advertising expenses, auctioneer's allowance, the expenses, if any required to correct any irregularity in the title, premium for Seller's bond, auditor's fee, attorney's fee, and all other expenses of sale occurred in and about the protection and execution of this contract, and all moneys advanced for taxes, assessments, insurance, and with interest thereon as provided herein, and all taxes due upon said land premises at time of sale, and to retain as compensation a commission of five percent (5%) on the amount of said sale or sales; SECOND, to pay the whole amount then remaining unpaid of the principal of said contract, and interest thereon to date of payment, whether the same shall be due or not, it being understood and agreed that upon such sale before maturity of the contract the balance thereof shall be immediately due and payable; THIRD, to pay liens of record against the security property according to their priority of lien and to the extent that funds remaining in the hands of the Seller are available; and LAST, to pay the remainder of said proceeds, if any, to the vendor, his heirs, personal representatives, successors or assigns upon the delivery and surrender to the vendee of possession of the land premises, less costs and excess of obtaining possession.

Is English Regular? ● The rat ran. ● The rat the cat saw ran. ● The rat the cat the dog chased saw ran. Let: A = {cat, rat, dog, bird, bug, pony} V = {ran, saw, chased, flew, sang, frolicked}. Let L = English {The A (that the A)* V* V}. L = {The A (that the A)n Vn V, n 0}. Let w = The cat (that the rat)k sawk ran.

Defining Functions from one Language to Another Let firstchars(L) = {w : y L ( y = cx, c L , x L*, and w c*)} Are the regular languages closed under firstchars? L a*b* ca*cb* firstchars(L)

Defining Functions from one Language to Another Let chop(L) = {w : x L ( x = x 1 cx 2, x 1 L*, x 2 L*, c L , |x 1| = |x 2|, and w = x 1 x 2)} Are the regular languages closed under chop? L a*b* a*db* chop(L)

Defining Functions from One Language to Another Let maxstring(L) = {w: w L, z * (z wz L)} Are the regular languages closed under maxstring? L a*b* ab*a a*b*a maxstring(L)

Defining Functions from One Language to Another Let mix(L) = {w: x, y, z ( x L, x = yz, |y| = |z|, w = yz. R)}. Are the regular languages closed under mix? L (a b)* (ab)*a(ab)* mix(L)