Philosophy 103 Linguistics 103 Yet still Even further

Philosophy 103 Linguistics 103 Yet, still, Even further More and yet more, ad infinitum, Introductory Logic: Critical Thinking Dr. Robert Barnard

Last Time: • Introduction to Categorical Logic • Categorical Propositions – Parts and Characteristics – Conditional and Conjunctive Equivalents – Existential Import

Plan for Today • Venn Diagrams for Propositions • Existential Import in Diagramming • Traditional Square of Opposition

REVIEW: THE 4 TYPES of CATEGORICAL PROPOSITION UNIVERSAL PARTICULAR AFFIRMATIVE ALL S is P SOME S is P NEGATIVE NO S is P SOME S is not P

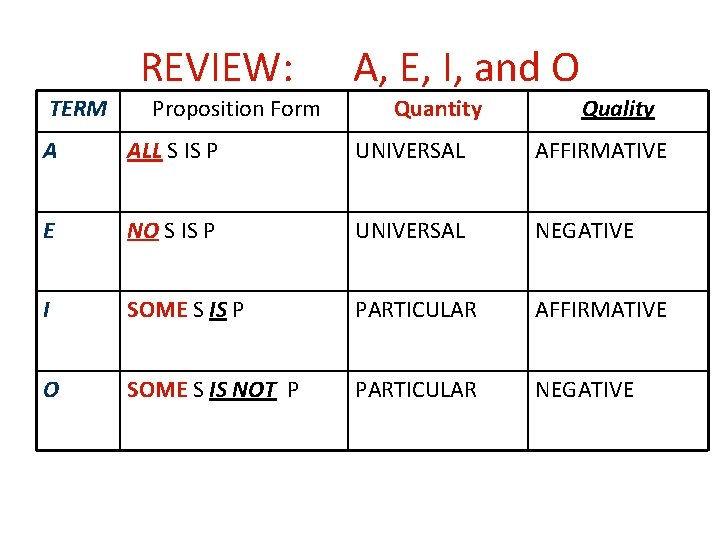
REVIEW: TERM Proposition Form A, E, I, and O Quantity Quality A ALL S IS P UNIVERSAL AFFIRMATIVE E NO S IS P UNIVERSAL NEGATIVE I SOME S IS P PARTICULAR AFFIRMATIVE O SOME S IS NOT P PARTICULAR NEGATIVE

Diagramming Propositions… Diagramming is a tool that can be used to make explicit information that is both descriptive and relational. • Geometric Diagrams • Blueprints • Road Maps • Flow Charts

…is FUN!!! We can also diagram CATEGORICAL PROPOSITIONS. They describe a relationship between the subject term (class) and the predicate term (class).

Focus on Standard Diagrams • Since there are 4 basic standard form categorical propositions, this means that there are exactly 4 standard diagrams for Categorical Propositions. • BUT – there are two flavors of diagrams we might use!

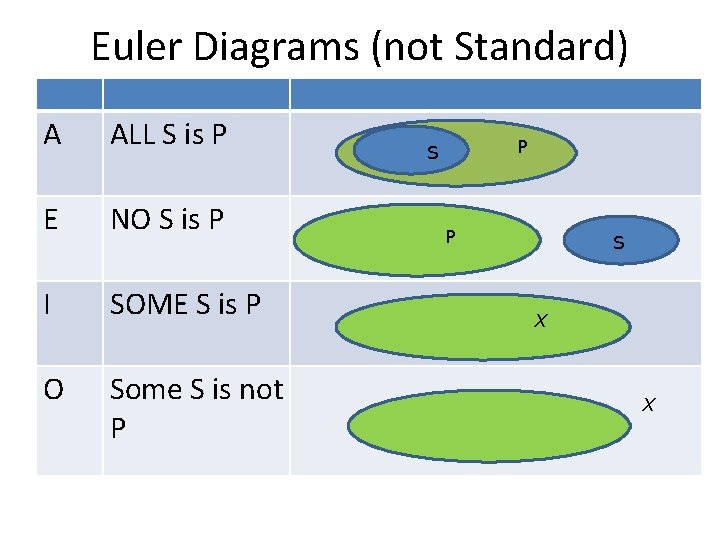
Euler Diagrams (not Standard) A ALL S is P E NO S is P I SOME S is P O Some S is not P P S X X

Pro and Cons: Pro: Euler Diagrams are very intuitive Con: Euler Diagrams can represent single propositions but are difficult to combine and apply to syllogisms. Con: Euler Diagrams Cannot capture Existential Import in both the Aristotelian AND Modern modes. (more later)

Alternative: Venn Diagrams • Venn Diagrams are less intuitive to some people than Euler Diagrams • Venn Diagrams Can easily be combined and used in Syllogisms. • Venn Diagrams CAN represent alternative modes of Existential Import.

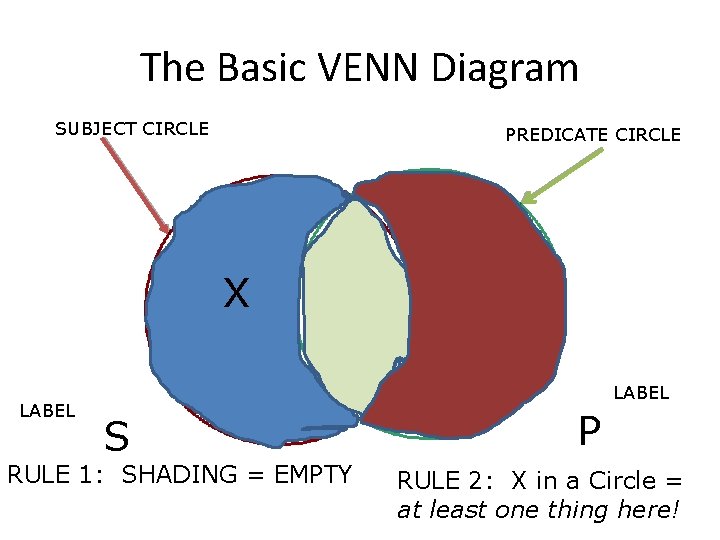
The Basic VENN Diagram SUBJECT CIRCLE PREDICATE CIRCLE X LABEL S RULE 1: SHADING = EMPTY P RULE 2: X in a Circle = at least one thing here!

Questions?

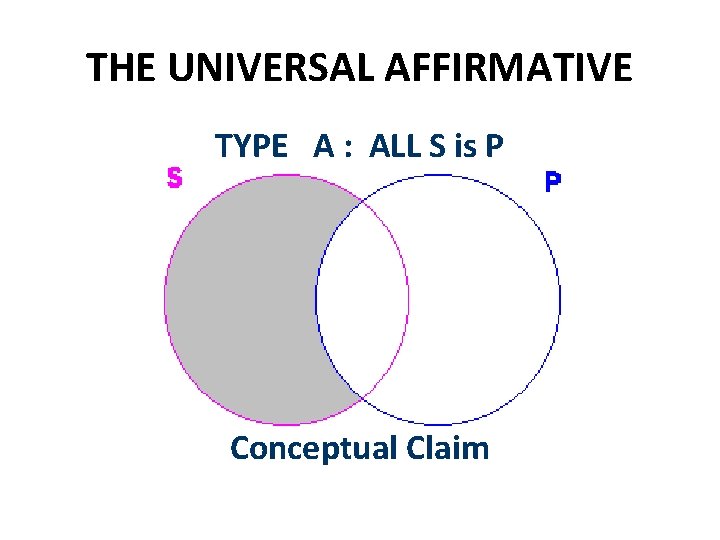
THE UNIVERSAL AFFIRMATIVE TYPE A : ALL S is P Conceptual Claim

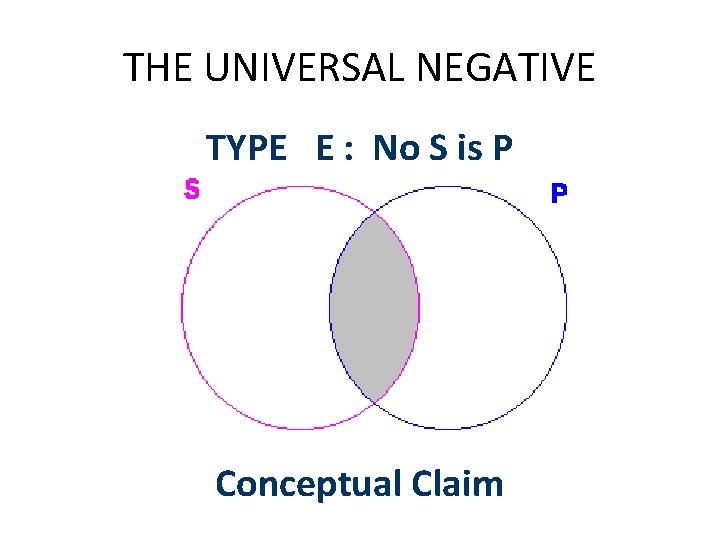
THE UNIVERSAL NEGATIVE TYPE E : No S is P Conceptual Claim

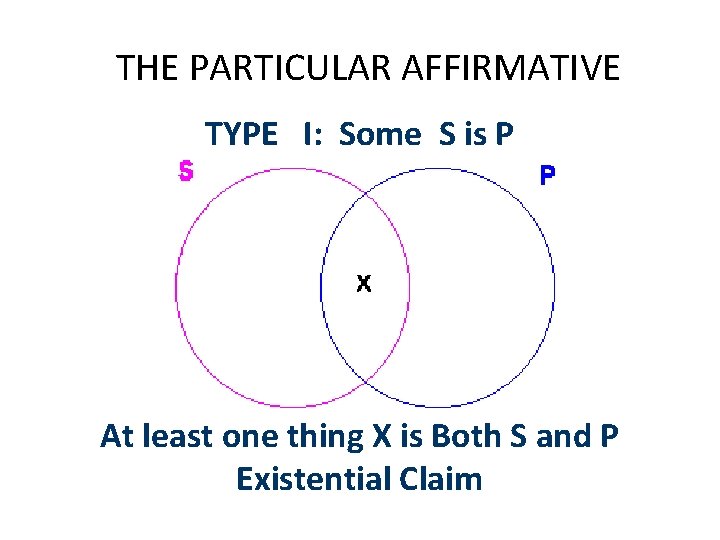
THE PARTICULAR AFFIRMATIVE TYPE I: Some S is P At least one thing X is Both S and P Existential Claim

THE PARTICULAR NEGATIVE TYPE O: Some S is not P At least one thing X is S and not P Existential Claim

EXISTENTIAL IMPORT ONLY a proposition with EXISTENTIAL IMPORT requires that there be an instance of the SUBJECT TERM in reality for the proposition to be true. Diagrams with an X indicate EXISTENTIAL IMPORT.

PROPOSITIONS ABOUT INDIVIDUALS In CATEGORICAL LOGIC a proper name denotes a class with one member. Fred Rodgers is Beloved by Millions Fred Beloved

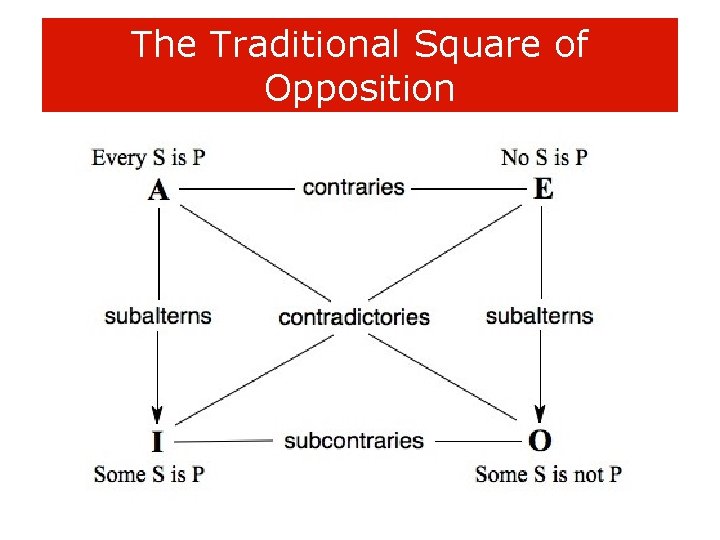
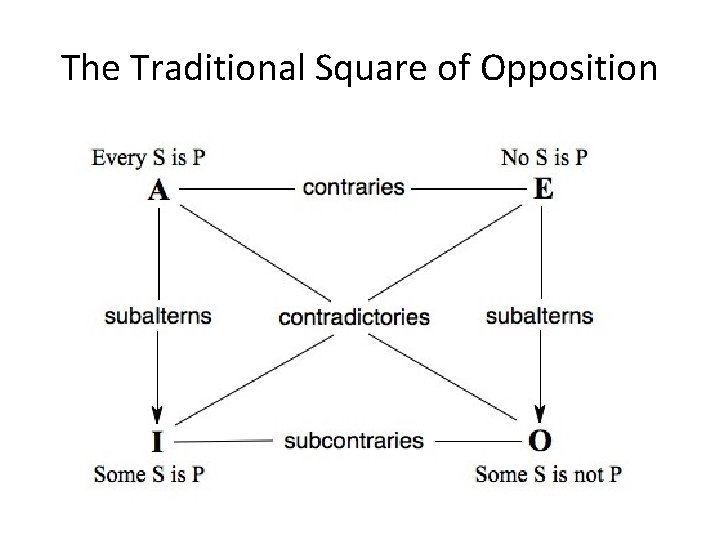
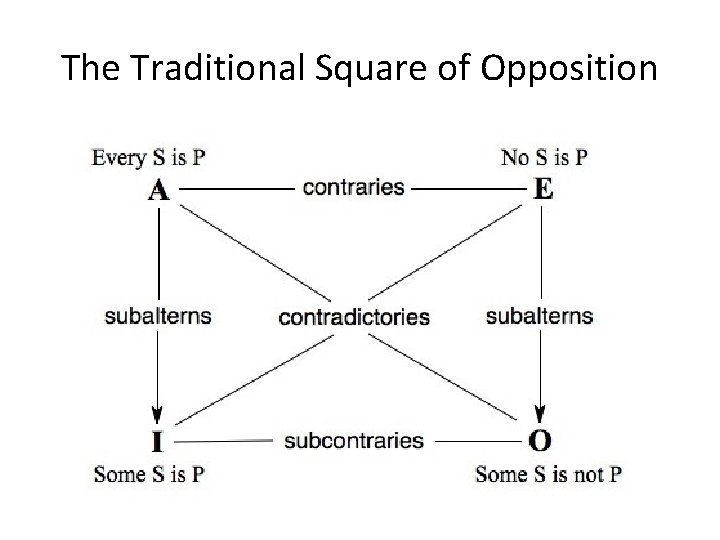
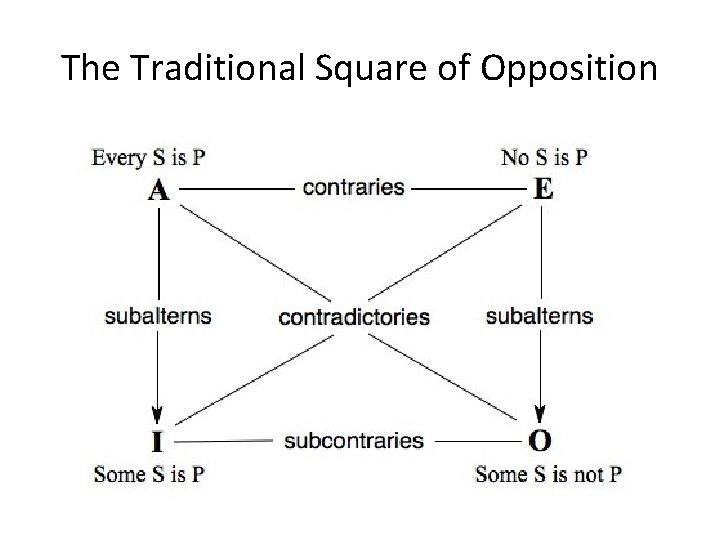
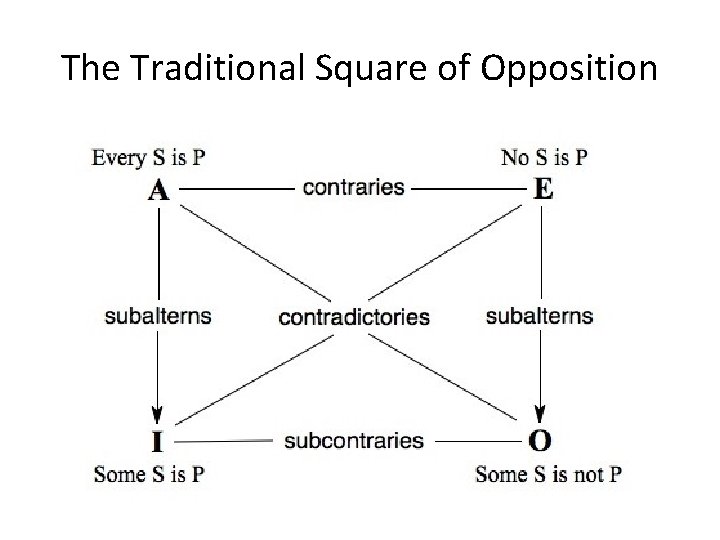
The Traditional Square of How are the 4 standard CPs related? Opposition

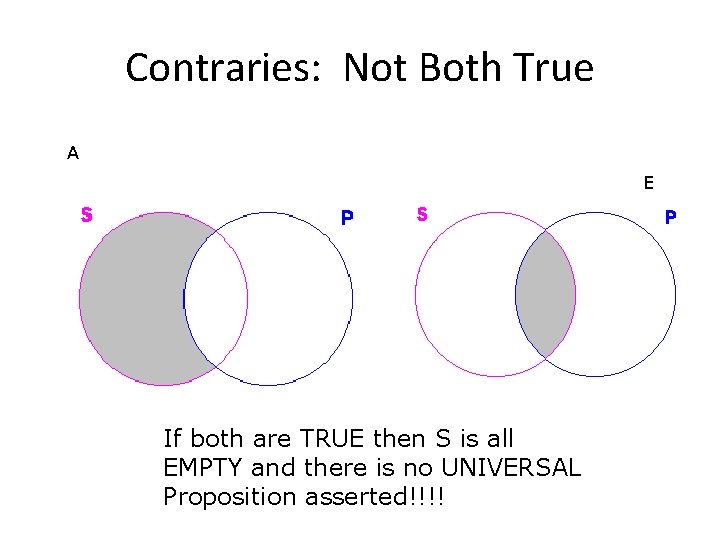
Contraries The A Proposition is related to the E proposition as a CONTRARY X is CONTRARY to Y = X and Y cannot both be true at the same time. Thus if A is true: E is False If E is True: A is False If A is False: E is UNDETERMINED

Contraries: Not Both True A E If both are TRUE then S is all EMPTY and there is no UNIVERSAL Proposition asserted!!!!

The Traditional Square of Opposition

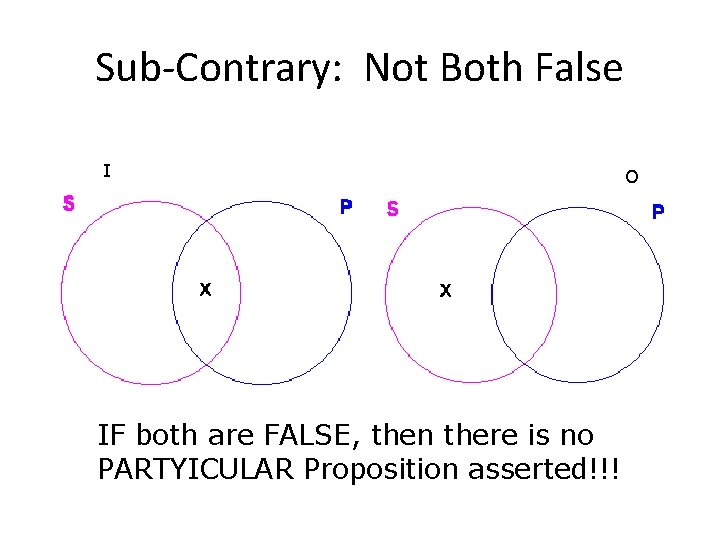
Sub-Contraries The SUBCONTRARY RELATION holds between the IProposition and the O-Proposition. Sub-Contrary = Not both False at the same time • If I is False then O is true • If O is False then I is true • If O (or I) is True, then I (or O) is undetermined

Sub-Contrary: Not Both False I IF both are FALSE, then there is no PARTYICULAR Proposition asserted!!! O

The Traditional Square of Opposition

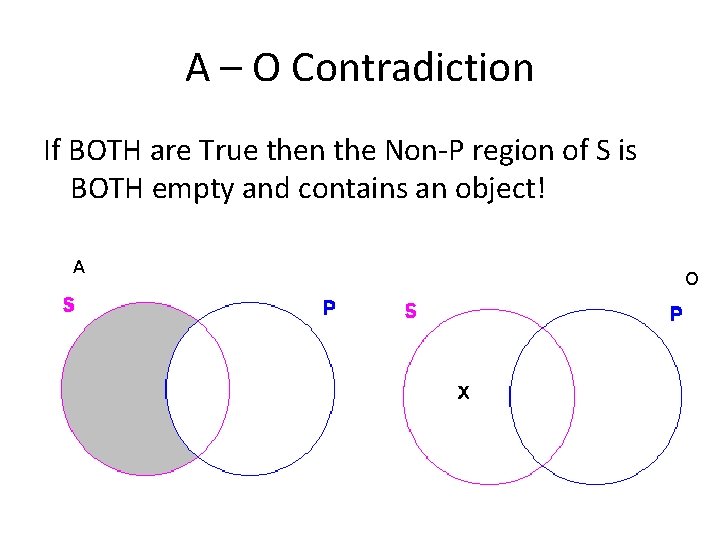
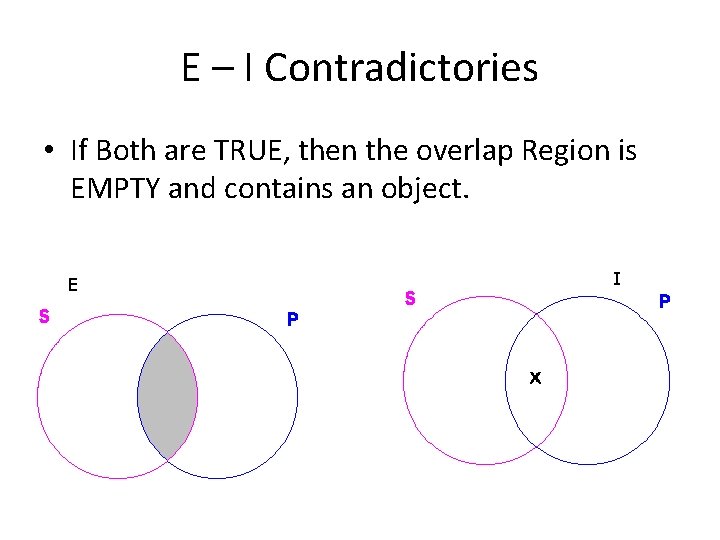
Contradictories Contradictory Propositions ALWAYS take opposite TRUTH VALUES • A and O are Contradictories • E and I are Contradictories

A – O Contradiction If BOTH are True then the Non-P region of S is BOTH empty and contains an object! A O

E – I Contradictories • If Both are TRUE, then the overlap Region is EMPTY and contains an object. E I

The Traditional Square of Opposition

Subalternation What is the relation between the UNIVERSAL and the PARTICULAR? • If All S is P, what about Some S is P? • If No S is P, what about Some S is not P? Subalternation claims that if the Universal is true, then the corresponding Particular is true.

Some Subalternations: • If All dogs are Brown, then Some dogs are brown. • If All Fish have Gills, then Some Fish have Gills. • If All Greeks are Brave, then Some Greeks are Brave

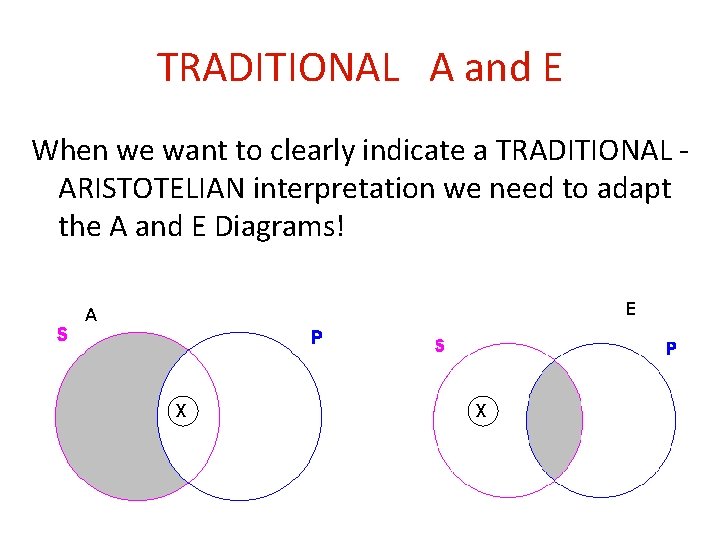
The TRADITIONAL Interpretation The TRADITIONAL or ARISTOTELIAN interpretation allows SUBALTERNATION Because FOR ARISTOTLE all category terms denote REAL objects. -- Every name picks out something in the world.

TRADITIONAL A and E When we want to clearly indicate a TRADITIONAL ARISTOTELIAN interpretation we need to adapt the A and E Diagrams! E A X X

The Traditional Square of Opposition

Questions?