Philosophy 103 Linguistics 103 Yet still Even further

Philosophy 103 Linguistics 103 Yet, still, Even further More and yet more, etc. , ad infinitum, Introductory Logic: Critical Thinking Dr. Robert Barnard

Last Time: • Venn Diagrams for Propositions • Existential Import in Diagramming • Traditional Square of Opposition

Plan for Today • Review: Venn Diagrams for Propositions • Modern Square of Opposition • The Existential Fallacy

Today is DAY 10 • In 10 Days an embryonic Chick goes from nothing to this: HAVE YOU DEVELOPED AS MUCH IN the LAST 10 Days? ? ?

REVIEW: THE 4 TYPES of CATEGORICAL PROPOSITION UNIVERSAL PARTICULAR AFFIRMATIVE ALL S is P SOME S is P NEGATIVE NO S is P SOME S is not P

REVIEW: TERM Proposition Form A, E, I, and O Quantity Quality A ALL S IS P UNIVERSAL AFFIRMATIVE E NO S IS P UNIVERSAL NEGATIVE I SOME S IS P PARTICULAR AFFIRMATIVE O SOME S IS NOT P PARTICULAR NEGATIVE

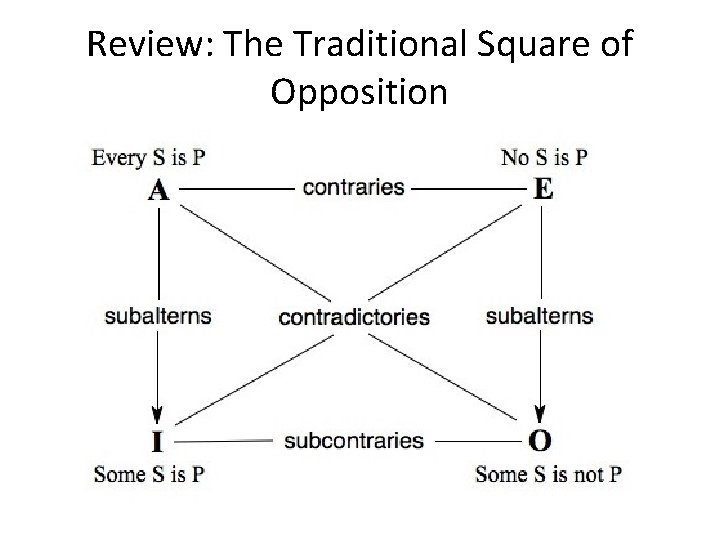
Review: The Traditional Square of Opposition

Subalternation What is the relation between the UNIVERSAL and the PARTICULAR? • If All S is P, what about Some S is P? • If No S is P, what about Some S is not P? Subalternation claims that if the Universal is true, then the corresponding Particular is true.

TRADITIONAL A and E In Traditional Logic we need to capture the Existential Assumption: That everything we can name with a category term or description, exists! E A X X

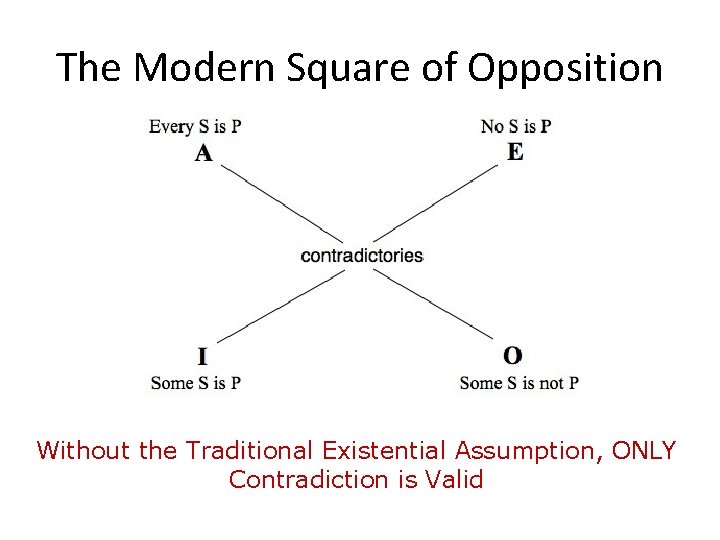
Traditional vs. Modern Categorical Logic The KEY difference between Traditional (Aristotelian) and Modern (Boolean) categorical Logic is that Traditional Logic ASSUMES that category terms all refer to actual objects. Modern Logic does NOT make the Existential Assumption.

Thanks to: George Boole • English Mathematician and Grandfather of computer Science. • Wrote The Laws of Thought (1854) • Invented Boolean Algebra 1815 -1864

Boole and the Existential Fallacy • Boole recognized that many Syllogistic Arguments assume that every category or class referred to is NON-EMPTY. • But it is possible to denote an EMPTY CLASS • What Happens to Categorical Logic if EMPTY CLASSES are allowed?

Traditional Square using Venn Diagrams X X The Existential Assumption allows the inference from Universal to Particular

Where is the Fallacy? Basically, the EXISTENTIAL FALLACY is this: 1. Deductive validity requires that it be IMPOSSIBLE to infer a FALSE CONCLUSION from TRUE PREMISES. 2. Reasoning by SUBALTERNATION always requires that the SUBJECT CLASS is non-empty. 3. It is POSSIBLE that a UNIVERSAL Proposition is true but has an empty SUBJECT CLASS 4. Therefore, it is possible to reason from True Premises to a false Conclusion by Subalternation. 5. So Subalternation is INVALID.

BUT Hurley Disagrees with ME!!! • The Author of our Logic Text claims that the Existential Fallacy only occurs when the subject is some sort of Mythic or Fictional being. • He thinks that traditional logic only sanctions SOME sub-alternations. • I disagree: I think Aristotle would not have drawn the line in THAT place. I think that relying upon individuals to decide on what is Mythic or Fictional takes us beyond LOGIC.

Take THAT Patrick J Hurley!

Avoiding the Existential Fallacy In order to avoid the Existential Fallacy we need to modify traditional categorical logic to remove the existential assumption. The Result is Modern or Boolean Categorical Logic

The Modern Square of Opposition Without the Traditional Existential Assumption, ONLY Contradiction is Valid

Modern Square using Venn Diagrams

Contradictories Contradictory Propositions ALWAYS take opposite TRUTH VALUES • A and O are Contradictories • E and I are Contradictories

Questions?

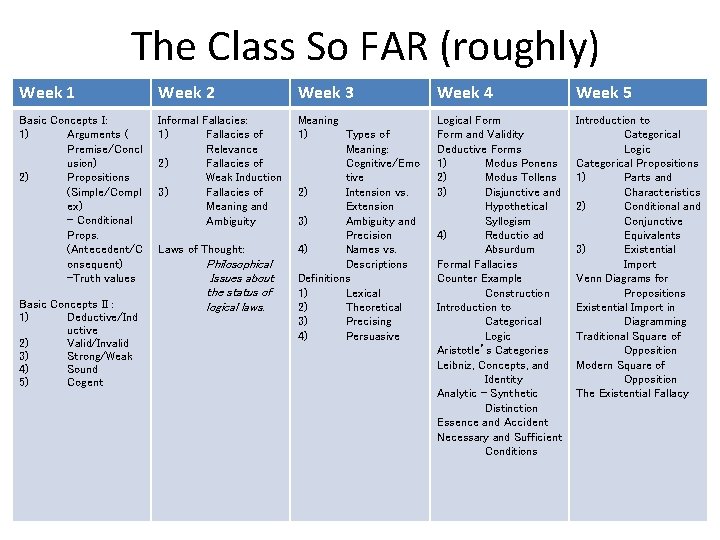
The Class So FAR (roughly) Week 1 Week 2 Week 3 Week 4 Week 5 Basic Concepts I: 1) Arguments ( Premise/Concl usion) 2) Propositions (Simple/Compl ex) - Conditional Props. (Antecedent/C onsequent) -Truth values Informal Fallacies: 1) Fallacies of Relevance 2) Fallacies of Weak Induction 3) Fallacies of Meaning and Ambiguity Meaning 1) Types of Meaning: Cognitive/Emo tive 2) Intension vs. Extension 3) Ambiguity and Precision 4) Names vs. Descriptions Definitions 1) Lexical 2) Theoretical 3) Precising 4) Persuasive Logical Form and Validity Deductive Forms 1) Modus Ponens 2) Modus Tollens 3) Disjunctive and Hypothetical Syllogism 4) Reductio ad Absurdum Formal Fallacies Counter Example Construction Introduction to Categorical Logic Aristotle’s Categories Leibniz, Concepts, and Identity Analytic – Synthetic Distinction Essence and Accident Necessary and Sufficient Conditions Introduction to Categorical Logic Categorical Propositions 1) Parts and Characteristics 2) Conditional and Conjunctive Equivalents 3) Existential Import Venn Diagrams for Propositions Existential Import in Diagramming Traditional Square of Opposition Modern Square of Opposition The Existential Fallacy Basic Concepts II : 1) Deductive/Ind uctive 2) Valid/Invalid 3) Strong/Weak 4) Sound 5) Cogent Laws of Thought: Philosophical Issues about the status of logical laws.

Next Week Tuesday: Mid Term Exam Thursday: Immediate Inferences in Categorical Logic

Test Format The Midterm will be 150 Points • • Section 1 (30 points) Basic Concepts/Vocabulary Section 2 (30 Points) Fallacies Section 3 (30 Points) Categorical Logic Concepts Section 4 (60 Points) Applications