Partial Molar Excess Quantities Notation convention Let G



















- Slides: 31

Partial Molar & Excess Quantities Notation convention Let G' stand for total free energy and in a similar fashion S', V', H', etc. Then we will let = G'/n represent the free energy per mole, n, and in a similar fashion. S', V', H', etc.

Consider a solution of volume V’ containing n, moles of a component 1, n 2 moles of a component 2 and etc. def Partial molar volume of component i

A Where the def the chemical potential of i Integrating the set of equation A , B etc

Differentiating the set and comparing A and B B etc Can also be written as Gibbs-Duhem eqns. *In the derivation of the Gibbs phase rule the Gibbs-Duhem eqns. play an important rule in restricting the allowed variations.

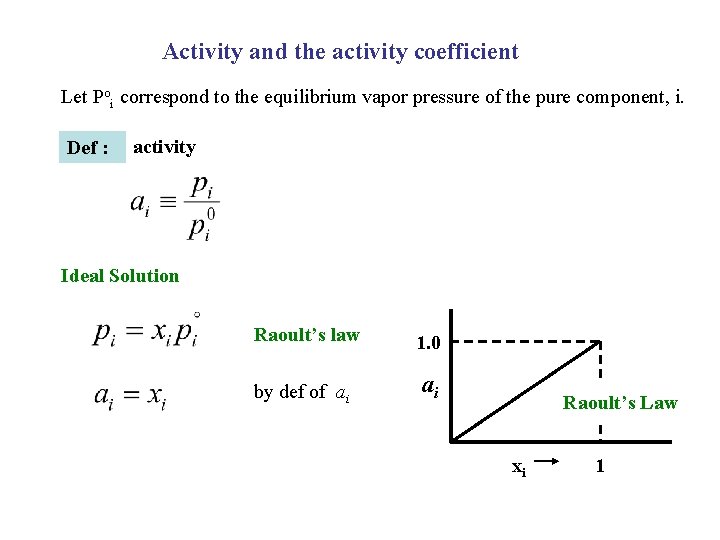
Activity and the activity coefficient Let Poi correspond to the equilibrium vapor pressure of the pure component, i. Def : activity Ideal Solution Raoult’s law 1. 0 by def of ai ai Raoult’s Law xi 1

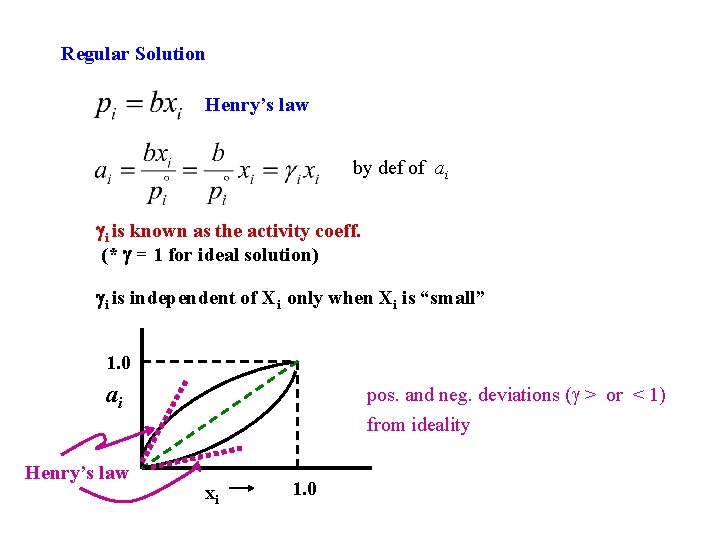
Regular Solution Henry’s law by def of ai gi is known as the activity coeff. (* g = 1 for ideal solution) gi is independent of Xi only when Xi is “small” 1. 0 ai Henry’s law pos. and neg. deviations ( > or < 1) from ideality xi 1. 0

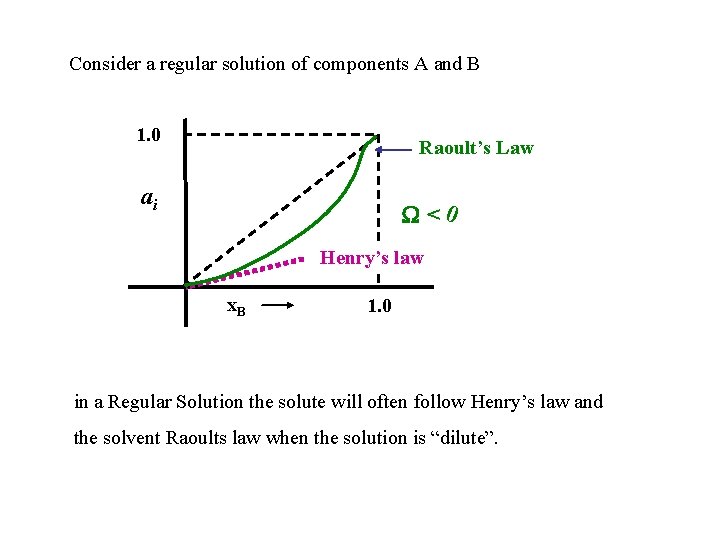
Consider a regular solution of components A and B 1. 0 Raoult’s Law ai <0 Henry’s law x. B 1. 0 in a Regular Solution the solute will often follow Henry’s law and the solvent Raoults law when the solution is “dilute”.

Partial molar Quantities in Ideal and regular solution Ideal Solution A We can also write the Gibbs potential as B Grouping terms in A and comparing coefficients of XA and XB in A and B Where and

Regular Solutions: A Using the identity Again comparing A and B This can be written in the form:

so that in the regular solution model: Summarizing Ideal Solution Regular Solution

How are the partial molar quantities related to the molar quantities ? Consider : Since x. A + x. B = 1 A

Also using and substituting for A from And similarly A

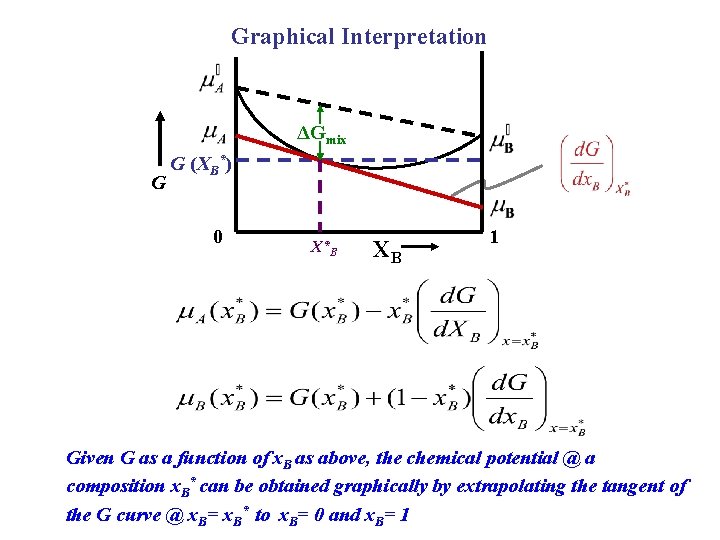
Graphical Interpretation ΔGmix G G (XB*) 0 X*B XB 1 Given G as a function of x. B as above, the chemical potential @ a composition x. B* can be obtained graphically by extrapolating the tangent of the G curve @ x. B= x. B* to x. B= 0 and x. B= 1

Chemical Equilibrium a. A + b. B + … x. X + y. Y + … A, B … reactants } standard states X, Y … products a, b, …. , x, y, …. Stoichiometric Coefficients Equilibrium is defined by the condition Since ≣ standard free energy change /mole

Solving for K is the equilibrium constant for the reaction. The equilibrium constant is defined by When components are not in standard state:

Equilibrium in multiphase Solutions Consider 2 phases containing the same component i in α and β The component i has and activity aαi and aβi. Imagine and infinitesimal amount of i is transferred from α to β so that the compositions have not been altered. The reaction is: The chemical potential of i in each phase is

The free energy change for the reaction at const T, P is, if => spontaneous (ΔG < 0) Equilibrium is defined by ΔG = 0 or ; In general for a multicomponent system with different phases present, equilibrium is defined by: … Equal P & T for all phases

The Gibbs Phase Rule Equilibrium for different phases, , …p in contact with one another is given by the conditions; A B C p phases present (p-1) eqns. for each component … C components present Equilibrium will in general not be maintained if the parameters are arbitrarily varied. The Gibbs phase rule restricts the manner in which the parameters can be varied such that equilibrium is maintained. The composition of a given phase is set by the additional condition. C - 1 composition variables per phase

The Gibbs Phase Rule For each phase there are (C – 1) + 2 = C + 1 independent variables or degrees of freedom. T, P The set of equations C represent a system of coupled linear equations. There are ( P – 1) equations for each component and C components so we have (P – 1)(C+2) equations. P (C +1) unknowns (P – 1)(C+2) equations In order for a solution to these equations to exist, # unknowns # of equations P (C +1) (P – 1)(C+2) P C+2

The Gibbs Phase Rule P C+2 For a system of C independent components not more than C + 2 phases can co-exist in equilibrium. Trivial Example: C = 1, P = 3 solid, liquid vapor If P is less than C + 2 then C + 2 – P variables can take on arbitrary values (degrees of freedom) without disturbing equilibrium. def. Thermodynamic degrees of freedom, f Gibbs Phase Rule

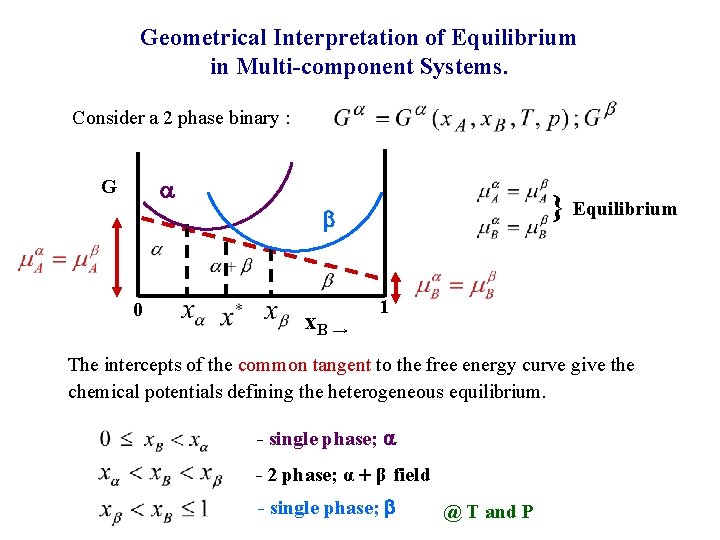
Geometrical Interpretation of Equilibrium in Multi-component Systems. Consider a 2 phase binary : a G 0 } Equilibrium b x. B → 1 The intercepts of the common tangent to the free energy curve give the chemical potentials defining the heterogeneous equilibrium. - single phase; a - 2 phase; α + β field - single phase; b @ T and P

Composition x* is in the 2 phase α + β field. Consider a simple rule of mixtures mass balance : fi is the fraction of alloy composed of i These formulas are analogous to mass balance for a lever with fulcrum @ x*. => “ Lever Rule”

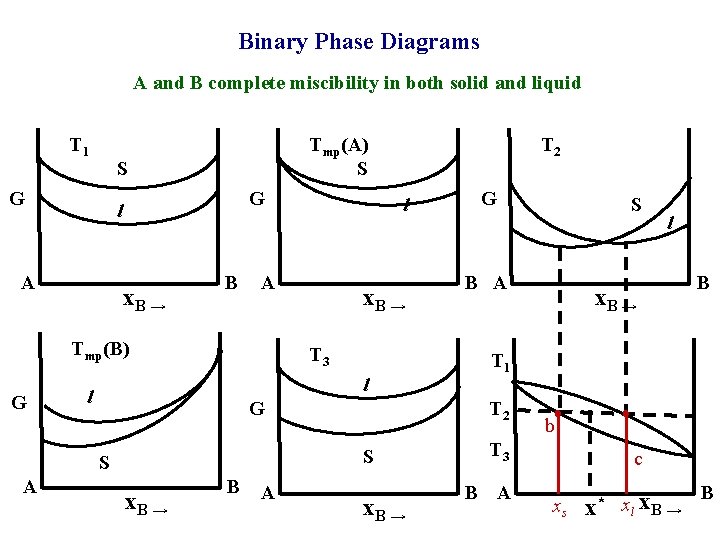
Binary Phase Diagrams A and B complete miscibility in both solid and liquid T 1 S G G l A x. B → B x. B → T 3 l l G x. B → B A G x. B → S B A l x. B → B T 1 T 2 S S A l A Tmp(B) G T 2 Tmp(A) S b T 3 B A c xs x* xl x. B → B

At temp T 2 x* is composed of some fl with composition c and fs at composition b: Lever Rule Ag-Au Si-Ge

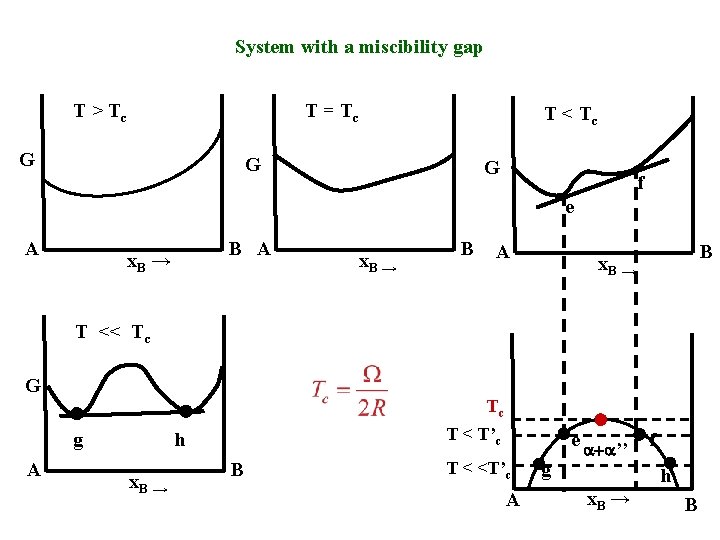
System with a miscibility gap T > Tc T = Tc G T < Tc G G f e A B A x. B → B A B x. B → T << Tc G Tc g A T < T’c h x. B → B T < <T’c A g e a+a’’ f h x. B → B

• The miscibility gap is the region where the overall composition exceeds the solubility limit. • The solid solution a is most stable as a mixture of two phases ’ + ’’. • Usually , ’, and ’’ have the same crystal structure. Cu –Pb, Au-Ni, Fe. Sn, Cr-W, Na. Cl-KCl, Ti. O 2 -Si. O 2.

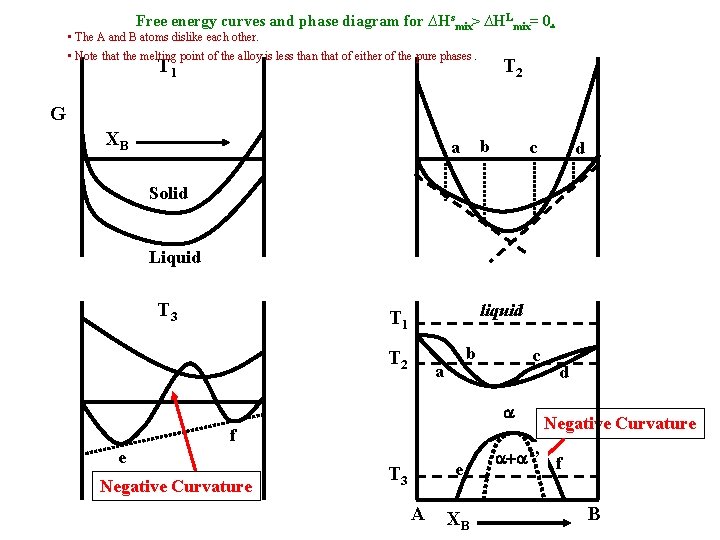
Free energy curves and phase diagram for ∆Hsmix> ∆HLmix= 0. • The A and B atoms dislike each other. • Note that the melting point of the alloy is less than that of either of the pure phases. T 2 T 1 G XB b a c d Solid Liquid T 3 liquid T 1 T 2 b a c a f e Negative Curvature e T 3 A XB d Negative Curvature a+a’’ f B

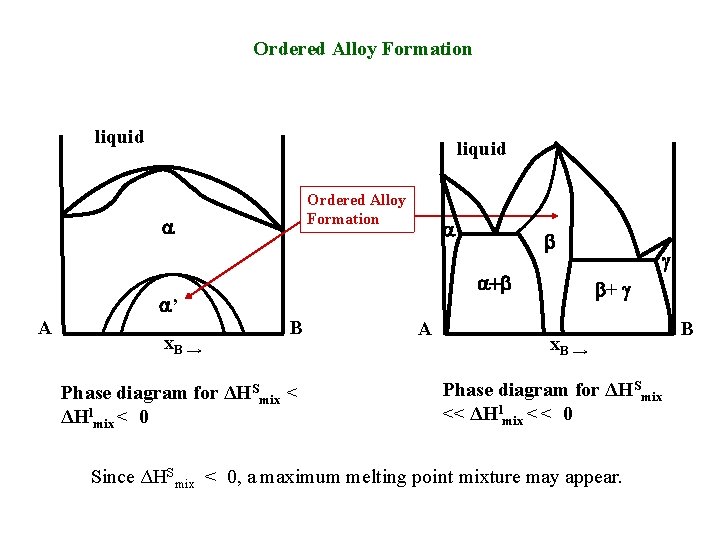
Ordered Alloy Formation liquid Ordered Alloy Formation a a a+b a’ A x. B → b B Phase diagram for ΔHSmix < ΔHlmix < 0 A g b+ g x. B → Phase diagram for ΔHSmix << ΔHlmix < < 0 Since ΔHSmix < 0, a maximum melting point mixture may appear. B

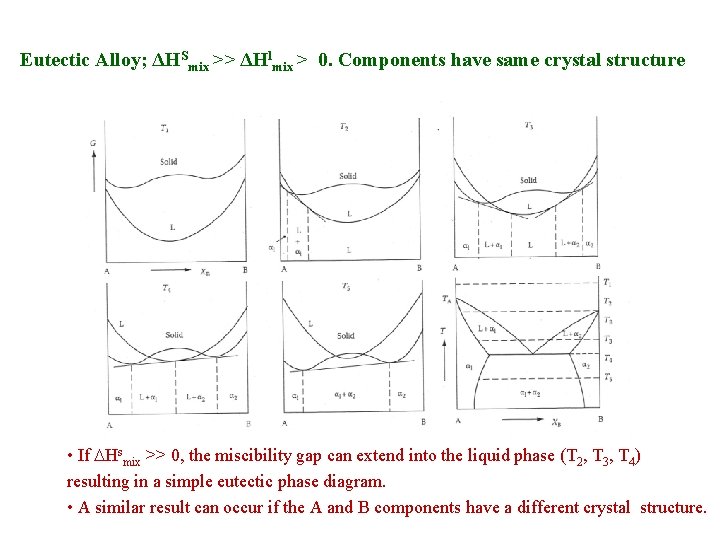
Eutectic Alloy; ΔHSmix >> ΔHlmix > 0. Components have same crystal structure • If Hsmix >> 0, the miscibility gap can extend into the liquid phase (T 2, T 3, T 4) resulting in a simple eutectic phase diagram. • A similar result can occur if the A and B components have a different crystal structure.

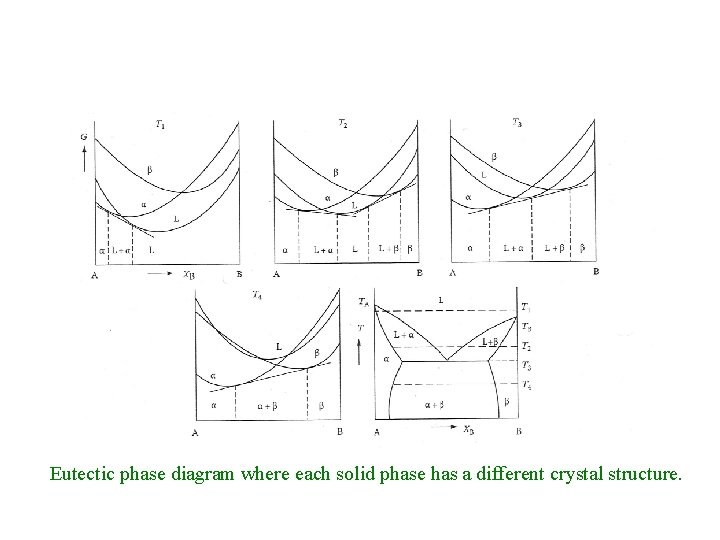
Eutectic phase diagram where each solid phase has a different crystal structure.

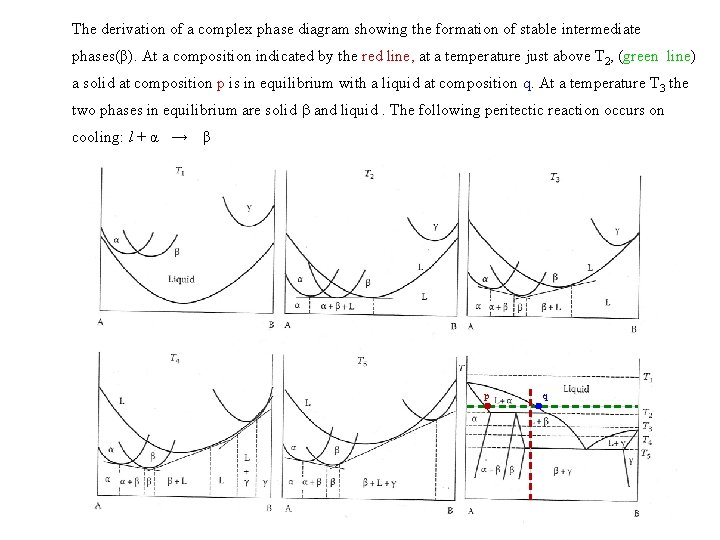
The derivation of a complex phase diagram showing the formation of stable intermediate phases(β). At a composition indicated by the red line, at a temperature just above T 2, (green line) a solid at composition p is in equilibrium with a liquid at composition q. At a temperature T 3 the two phases in equilibrium are solid and liquid. The following peritectic reaction occurs on cooling: l + α → β p q
 Partial molar quantities
Partial molar quantities Partial molar quantities
Partial molar quantities Partial molar volume
Partial molar volume Define partial molar quantities
Define partial molar quantities Let me let me let me
Let me let me let me Relation between linear and angular quantities
Relation between linear and angular quantities Excess 4 notation
Excess 4 notation Which excess notation is used to represent zero as 10000
Which excess notation is used to represent zero as 10000 Partial molar pregnancy
Partial molar pregnancy Antecenent
Antecenent Partial molar pregnancy
Partial molar pregnancy Prefix postfix infix conversion
Prefix postfix infix conversion Reverse polish notation
Reverse polish notation Reversed polish notation expression
Reversed polish notation expression How would 13800 volts be written in metric notation
How would 13800 volts be written in metric notation Let's go to my house
Let's go to my house Let him who has ears to hear
Let him who has ears to hear Me te le nos les
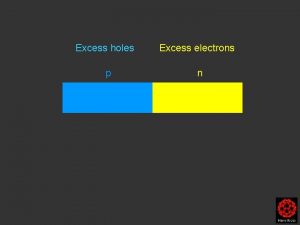
Me te le nos les Haynes shockley experiment
Haynes shockley experiment Jettison excess baggage
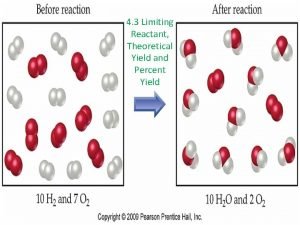
Jettison excess baggage How to calculate excess reactant
How to calculate excess reactant What is equilibrium cant
What is equilibrium cant Konversi bilangan desimal 9 menjadi kode excess-3 adalah
Konversi bilangan desimal 9 menjadi kode excess-3 adalah Reserve ratio formula
Reserve ratio formula How to find excess reserves
How to find excess reserves Excess reagent def
Excess reagent def How to find excess reactant
How to find excess reactant Excess capacity
Excess capacity Molecular sieve
Molecular sieve Excess heat reduce
Excess heat reduce Banana split method limiting reagent
Banana split method limiting reagent Limiting reagent
Limiting reagent