Parallel Lines and Proportional Parts Section 7 4

Parallel Lines and Proportional Parts Section 7. 4

Proportional parts of triangles • Non parallel transversals that intersect parallel lines can be extended to form similar triangles. • So, the sides of the triangles are proportional.

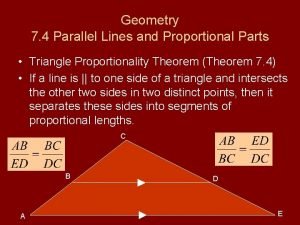
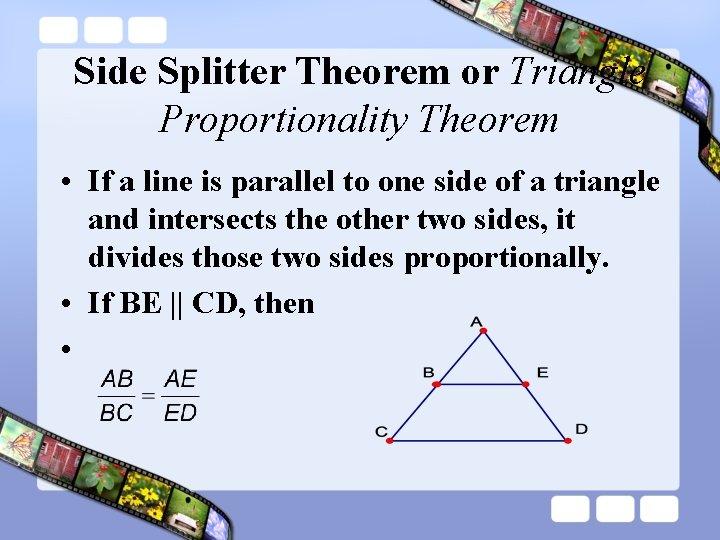
Side Splitter Theorem or Triangle Proportionality Theorem • If a line is parallel to one side of a triangle and intersects the other two sides, it divides those two sides proportionally. • If BE || CD, then •

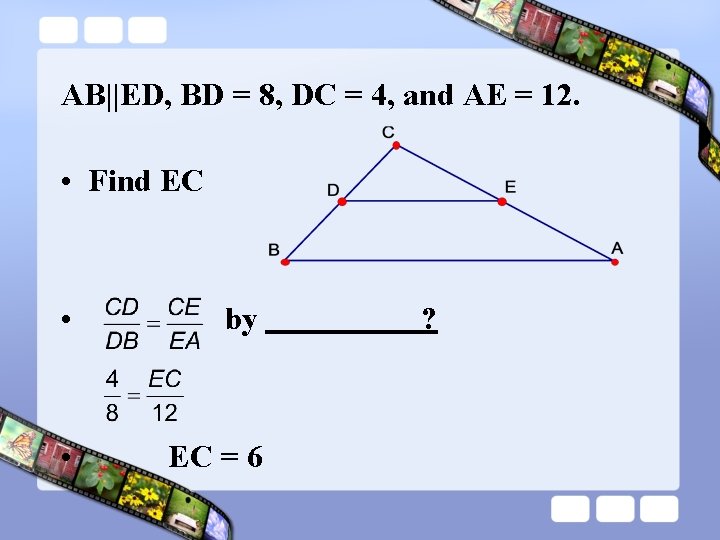
AB||ED, BD = 8, DC = 4, and AE = 12. • Find EC • by • EC = 6 ?

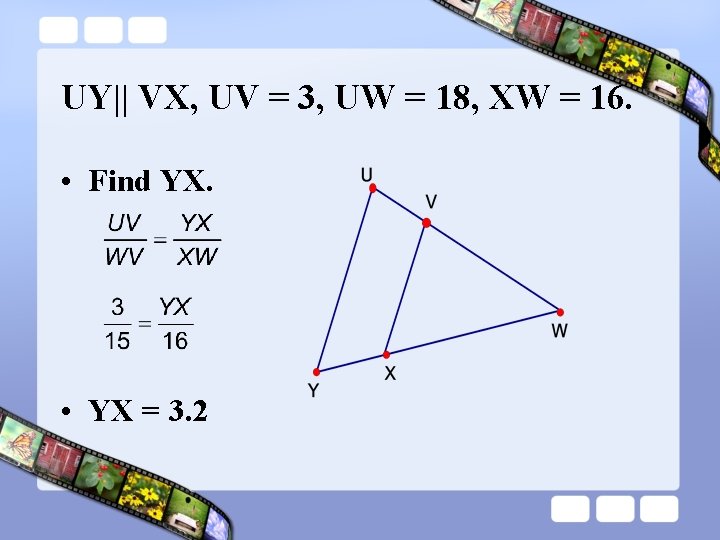
UY|| VX, UV = 3, UW = 18, XW = 16. • Find YX. • YX = 3. 2

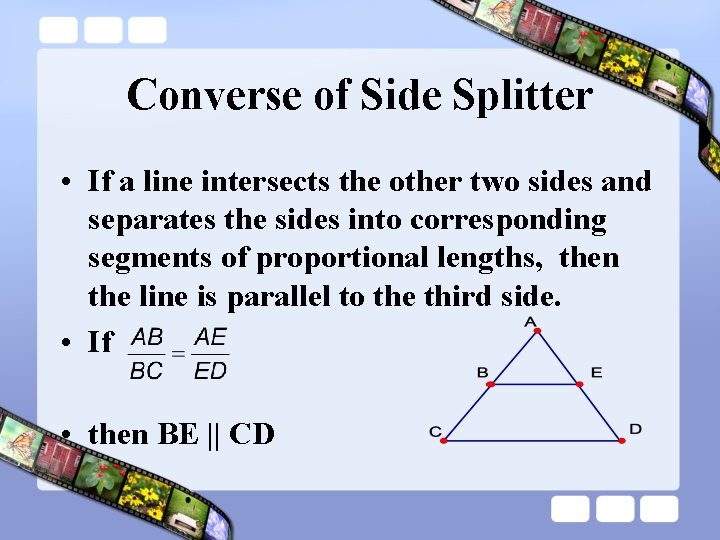
Converse of Side Splitter • If a line intersects the other two sides and separates the sides into corresponding segments of proportional lengths, then the line is parallel to the third side. • If • then BE || CD

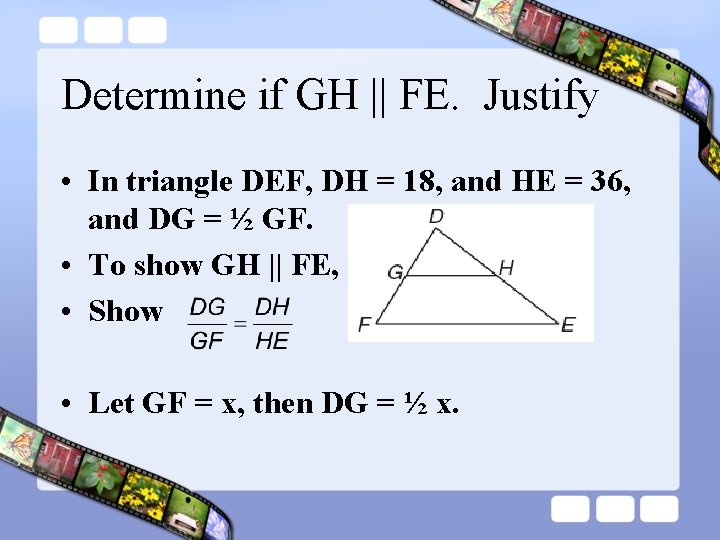
Determine if GH || FE. Justify • In triangle DEF, DH = 18, and HE = 36, and DG = ½ GF. • To show GH || FE, • Show • Let GF = x, then DG = ½ x.

• Substitute • Simplify

• Since the sides are proportional, then GH || FE.

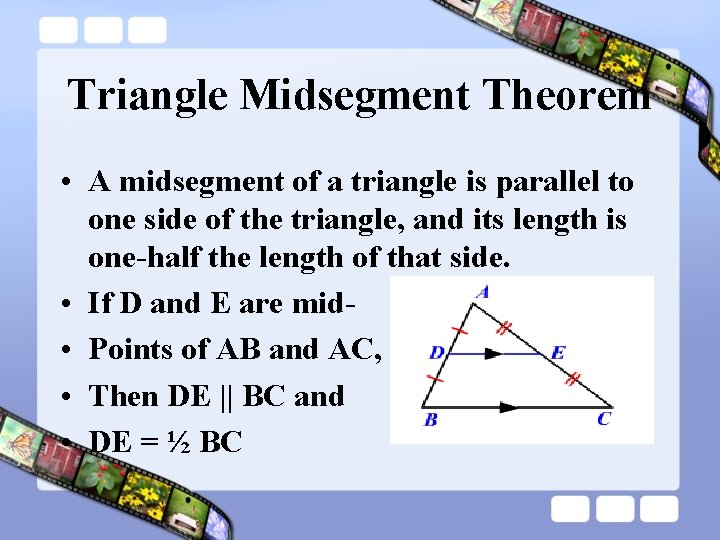
Triangle Midsegment Theorem • A midsegment of a triangle is parallel to one side of the triangle, and its length is one-half the length of that side. • If D and E are mid • Points of AB and AC, • Then DE || BC and • DE = ½ BC

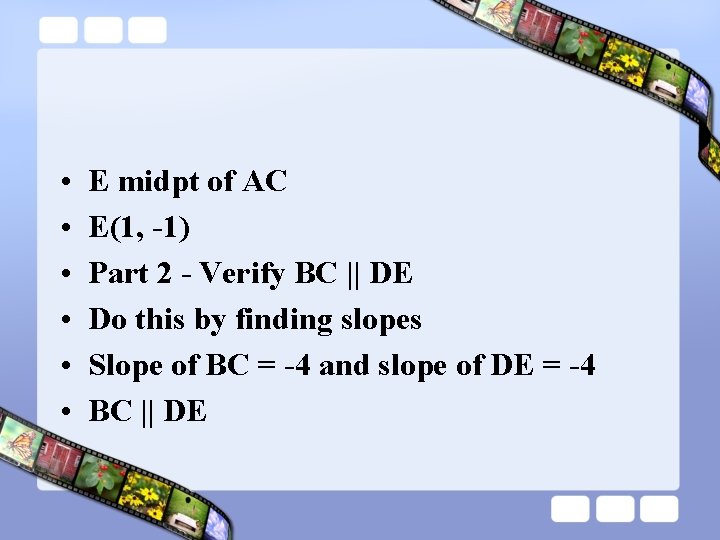
Example • Triangle ABC has vertices A(-2, 2), B(2, 4) and C(4, -4). DE is the midsegment of triangle ABC. • Find the coordinates of D and E. • D midpt of AB • D(0, 3) •

• • • E midpt of AC E(1, -1) Part 2 - Verify BC || DE Do this by finding slopes Slope of BC = -4 and slope of DE = -4 BC || DE

• • • Part 3 – Verify DE = ½ BC To do this use the distance formula BC = which simplifies to DE = ½ BC

Corollaries of side splitter thm. • 1. If three or more parallel lines intersect two transversals, then they cut off the transversals proportionally.

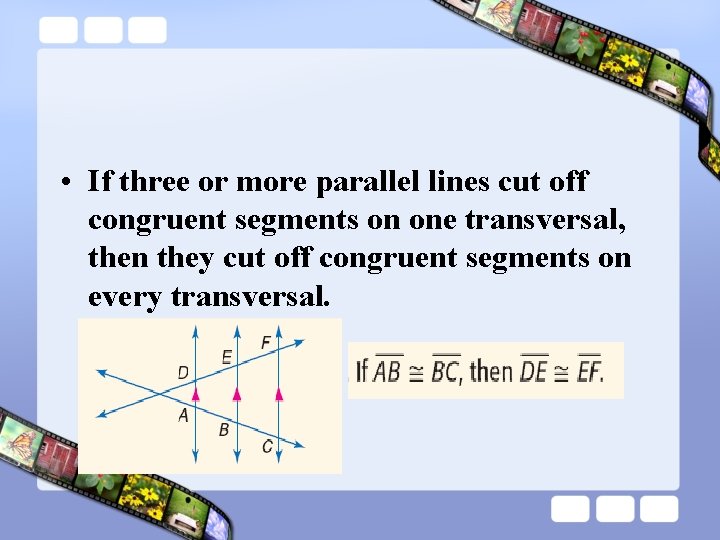
• If three or more parallel lines cut off congruent segments on one transversal, then they cut off congruent segments on every transversal.

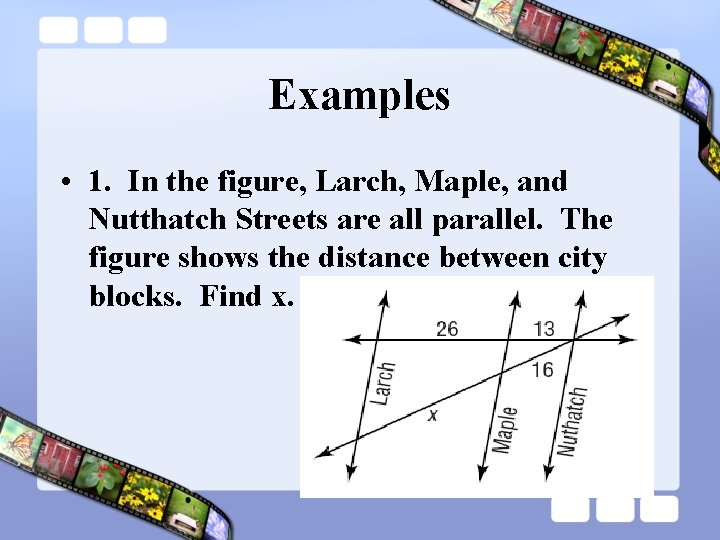
Examples • 1. In the figure, Larch, Maple, and Nutthatch Streets are all parallel. The figure shows the distance between city blocks. Find x.

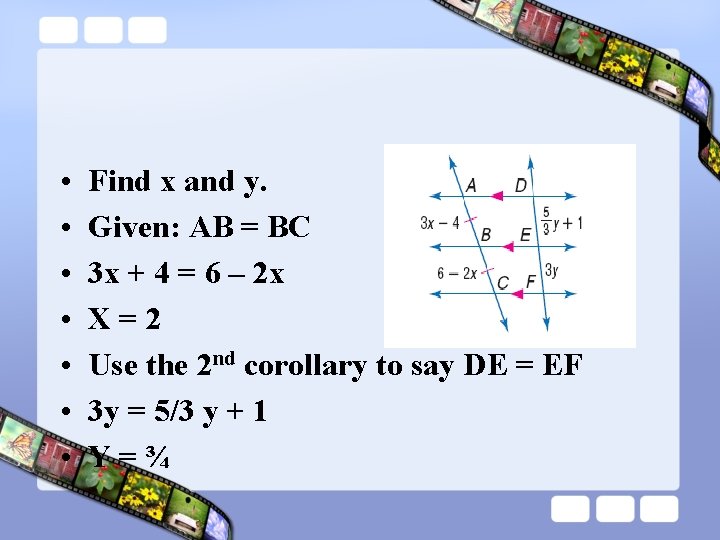
• • Find x and y. Given: AB = BC 3 x + 4 = 6 – 2 x X=2 Use the 2 nd corollary to say DE = EF 3 y = 5/3 y + 1 Y=¾