Lesson 6 4 Parallel Lines and Proportional Parts

Ohio Content Standards: Estimate, compute and solve problems involving real numbers, including ratio, proportion

Ohio Content Standards: Estimate, compute and solve problems involving rational numbers, including ratio, proportion

Ohio Content Standards: Use proportional reasoning and apply indirect measurement techniques, including right triangle

Ohio Content Standards: Use scale drawings and right triangle trigonometry to solve problems that

Ohio Content Standards: Apply proportional reasoning to solve problems involving indirect measurements or rates.

Theorem 6. 4 Triangle Proportionality Theorem

Theorem 6. 4 Triangle Proportionality Theorem If a line is parallel to one side

Theorem 6. 4 Triangle Proportionality Theorem C B A D E

Theorem 6. 5 Converse of the Triangle Proportionality Theorem

Theorem 6. 5 Converse of the Triangle Proportionality Theorem If a line intersects two

Theorem 6. 5 Converse of the Triangle Proportionality Theorem C B A D E

Midsegment A segment whose endpoints are the midpoints of two sides of the triangle.

Theorem 6. 6 Triangle Midsegment Theorem

Theorem 6. 6 Triangle Midsegment Theorem A midsegment of a triangle is parallel to

Theorem 6. 6 Triangle Midsegment Theorem C B A D E

Triangle ABC has vertices A(-2, 2), B(2, 4), and C(4, -4). DE is a

Corollary 6. 1 If three or more parallel lines intersect two transversals, then they

Corollary 6. 2 If three or more parallel lines cut off congruent segments on

In the figure, Larch, Maple, and Hatch Streets are all parallel. The figure shows

Assignment: Pgs. 312 -315 14 -28 evens, 50 -56 evens

Slides: 33

Download presentation

Lesson 6 -4 Parallel Lines and Proportional Parts

Ohio Content Standards:

Ohio Content Standards: Estimate, compute and solve problems involving real numbers, including ratio, proportion and percent, and explain solutions.

Ohio Content Standards: Estimate, compute and solve problems involving rational numbers, including ratio, proportion and percent, and judge the reasonableness of solutions.

Ohio Content Standards: Use proportional reasoning and apply indirect measurement techniques, including right triangle trigonometry and properties of similar triangles, to solve problems involving measurements and rates.

Ohio Content Standards: Use scale drawings and right triangle trigonometry to solve problems that include unknown distances and angle measures.

Ohio Content Standards: Apply proportional reasoning to solve problems involving indirect measurements or rates.

Theorem 6. 4 Triangle Proportionality Theorem

Theorem 6. 4 Triangle Proportionality Theorem If a line is parallel to one side of a triangle and intersects the other two sides in two distinct points, then it separates these sides into segments of proportional lengths.

Theorem 6. 4 Triangle Proportionality Theorem C B A D E

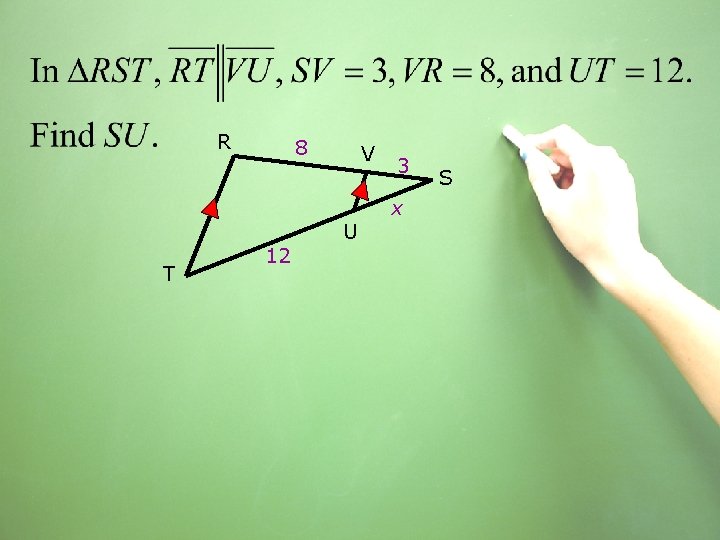
R T 8 12 V U 3 x S

Theorem 6. 5 Converse of the Triangle Proportionality Theorem

Theorem 6. 5 Converse of the Triangle Proportionality Theorem If a line intersects two sides of a triangle and separates the sides into corresponding segments of proportional lengths, then the line is parallel to the third side.

Theorem 6. 5 Converse of the Triangle Proportionality Theorem C B A D E

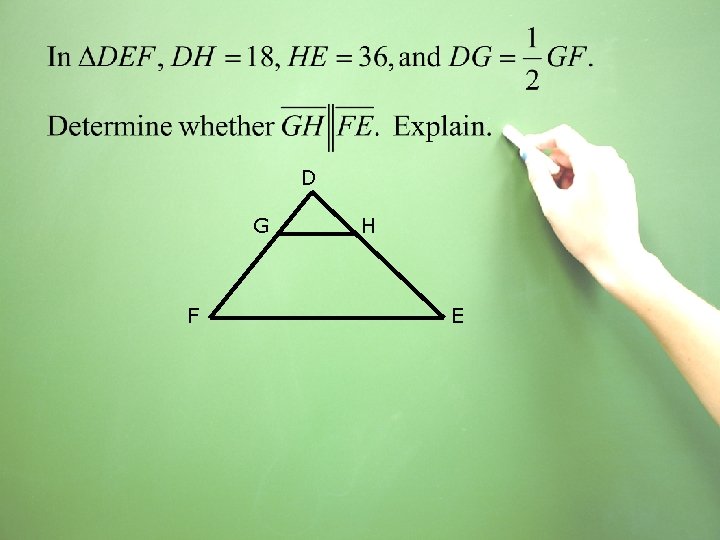
D G F H E

Midsegment

Midsegment A segment whose endpoints are the midpoints of two sides of the triangle.

Theorem 6. 6 Triangle Midsegment Theorem

Theorem 6. 6 Triangle Midsegment Theorem A midsegment of a triangle is parallel to one side of the triangle, and its length is one-half the length of that side.

Theorem 6. 6 Triangle Midsegment Theorem C B A D E

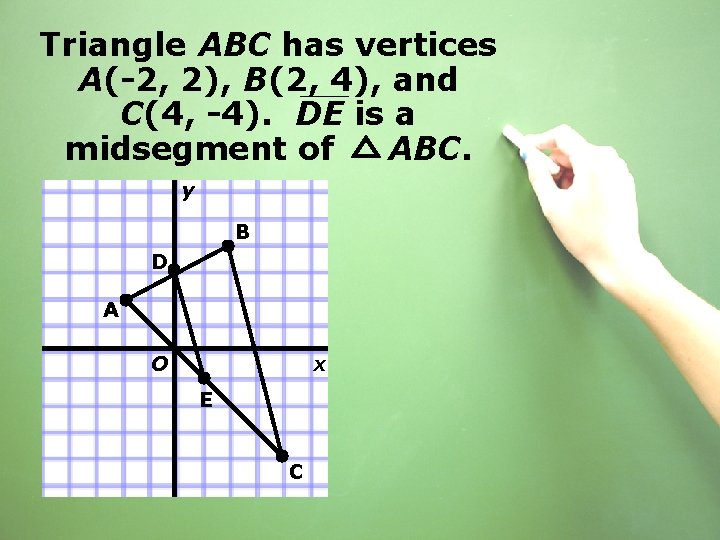
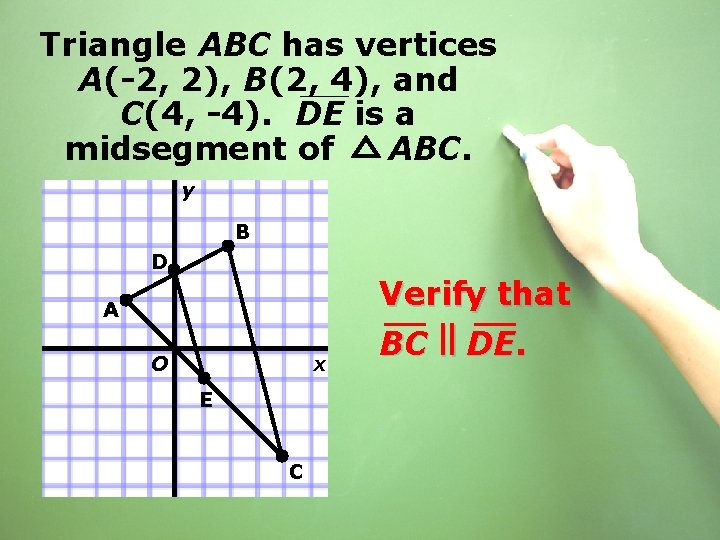
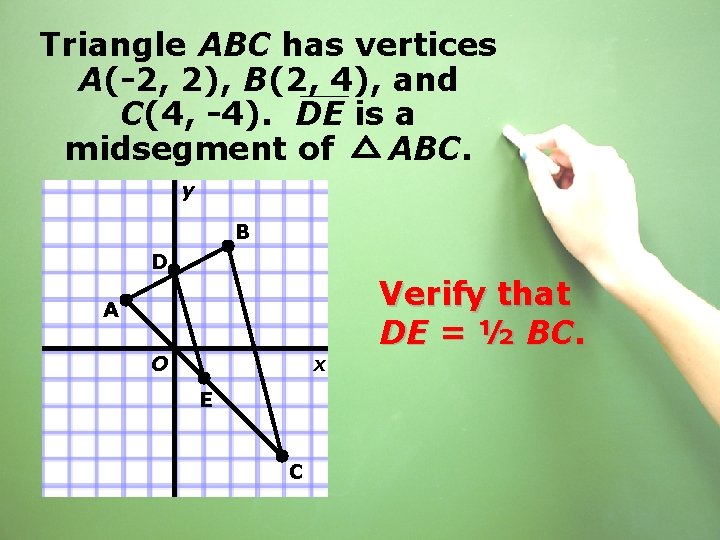
Triangle ABC has vertices A(-2, 2), B(2, 4), and C(4, -4). DE is a midsegment of ABC. y B D A O x E C

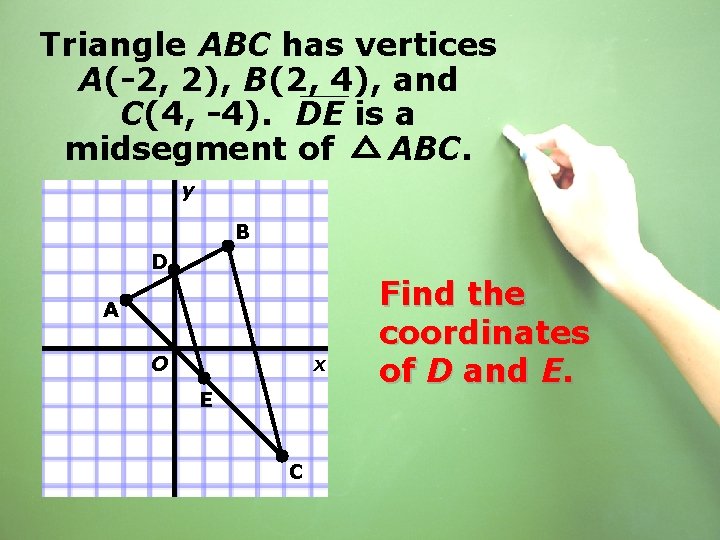
Triangle ABC has vertices A(-2, 2), B(2, 4), and C(4, -4). DE is a midsegment of ABC. y B D A O x E C Find the coordinates of D and E.

Triangle ABC has vertices A(-2, 2), B(2, 4), and C(4, -4). DE is a midsegment of ABC. y B D Verify that A O x E C BC ll DE.

Triangle ABC has vertices A(-2, 2), B(2, 4), and C(4, -4). DE is a midsegment of ABC. y B D A O x E C Verify that DE = ½ BC.

Corollary 6. 1

Corollary 6. 1 If three or more parallel lines intersect two transversals, then they cut off the transversals proportionally.

Corollary 6. 1 D A E B F C

Corollary 6. 2

Corollary 6. 2 If three or more parallel lines cut off congruent segments on one transversal, then they cut off congruent segments on every transversal.

Corollary 6. 2 D A E B F C

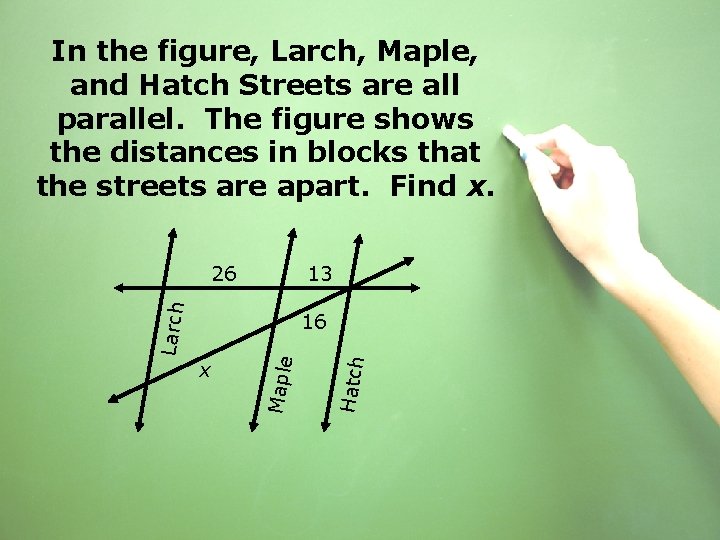
In the figure, Larch, Maple, and Hatch Streets are all parallel. The figure shows the distances in blocks that the streets are apart. Find x. 13 Larch 26 Hatch x Maple 16

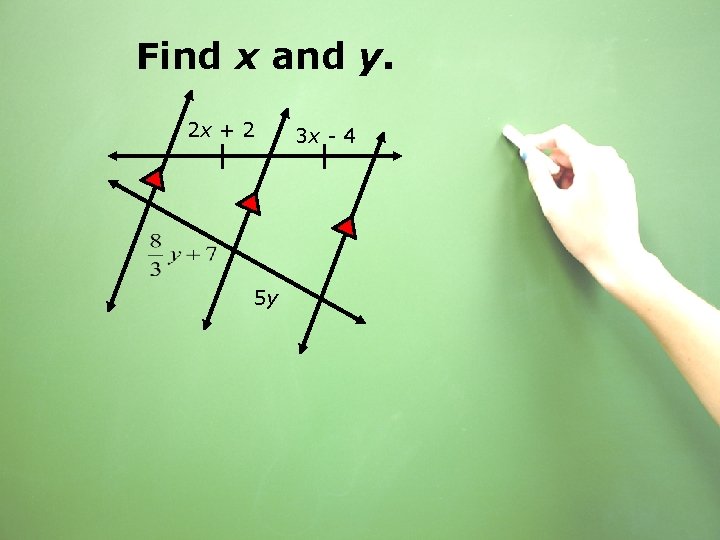
Find x and y. 2 x + 2 5 y 3 x - 4

Assignment: Pgs. 312 -315 14 -28 evens, 50 -56 evens