3 2 Use Parallel Lines and Transversals Postulate

3. 2 – Use Parallel Lines and Transversals Example 1: Identify congruent angles The

3. 2 – Use Parallel Lines and Transversals Theorem 3. 1 – Alternate Interior

3. 2 – Use Parallel Lines and Transversals Theorem 3. 1 – Alternate Exterior

3. 2 – Use Parallel Lines and Transversals Theorem 3. 1 – Consecutive Interior

3. 2 – Use Parallel Lines and Transversals Example 2 – Use properties of

3. 2 – Use Parallel Lines and Transversals Example 3 – Use properties of

3. 2 – Use Parallel Lines and Transversals Example 4 – Use properties of

3. 2 – Use Parallel Lines and Transversals Example 5 – Use properties of

3. 2 – Use Parallel Lines and Transversals Example 6 – Use properties of

3. 2 – Use Parallel Lines and Transversals Example 7 – Use properties of

3. 2 – Use Parallel Lines and Transversals Example 8 – Prove the Alternate

3. 2 – Use Parallel Lines and Transversals Example 9 – Solve a real

Slides: 13

Download presentation

3. 2 – Use Parallel Lines and Transversals Postulate 15 – Corresponding Angles Postulate If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.

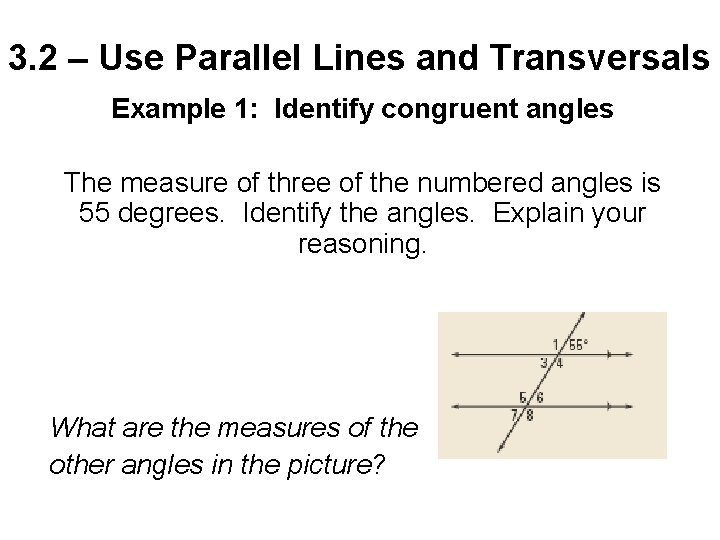
3. 2 – Use Parallel Lines and Transversals Example 1: Identify congruent angles The measure of three of the numbered angles is 55 degrees. Identify the angles. Explain your reasoning. What are the measures of the other angles in the picture?

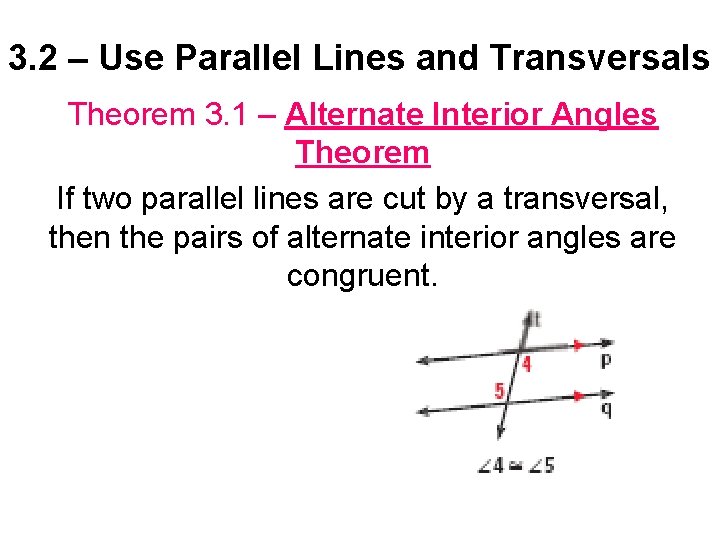
3. 2 – Use Parallel Lines and Transversals Theorem 3. 1 – Alternate Interior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.

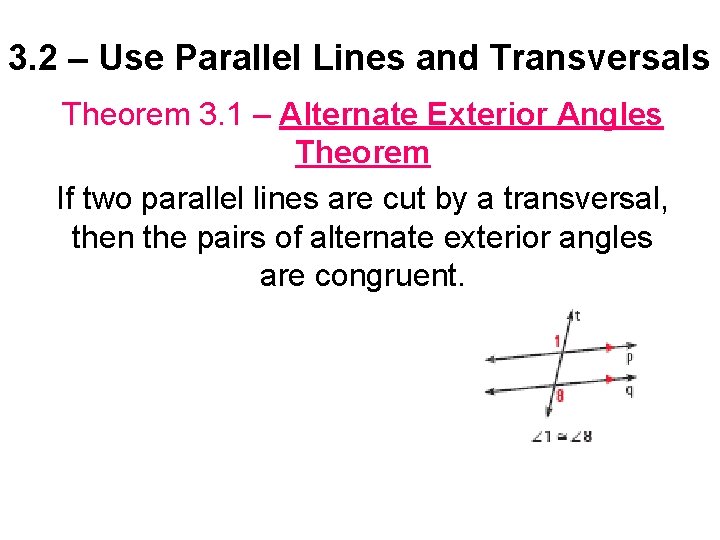
3. 2 – Use Parallel Lines and Transversals Theorem 3. 1 – Alternate Exterior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.

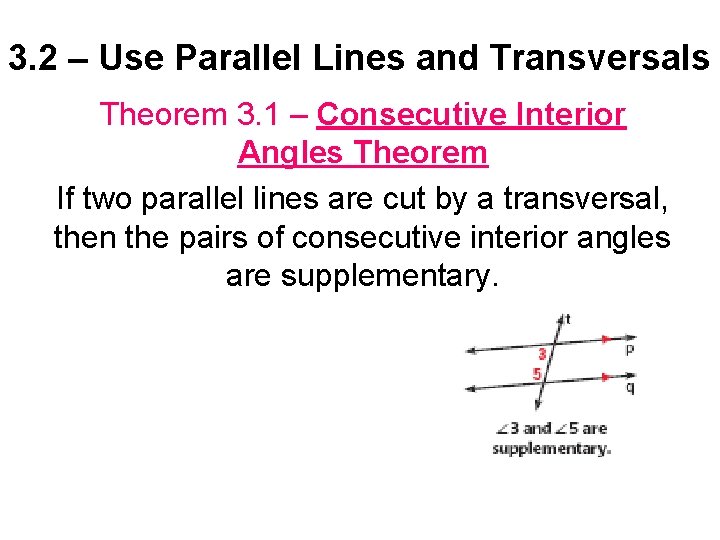
3. 2 – Use Parallel Lines and Transversals Theorem 3. 1 – Consecutive Interior Angles Theorem If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary.

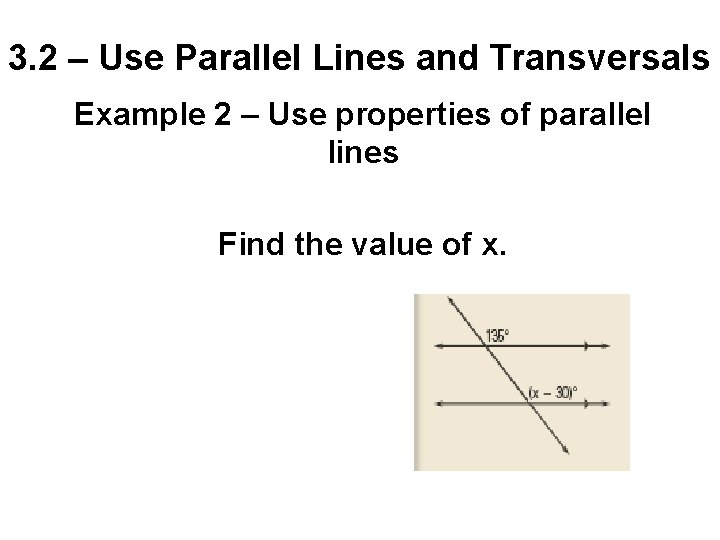
3. 2 – Use Parallel Lines and Transversals Example 2 – Use properties of parallel lines Find the value of x.

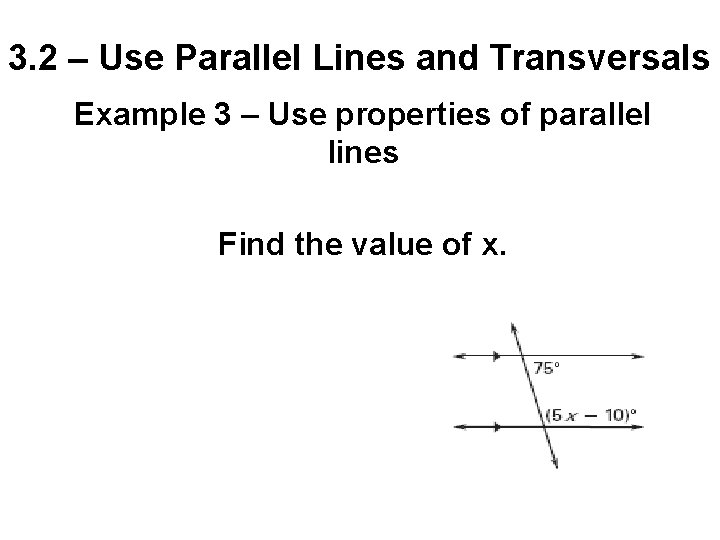
3. 2 – Use Parallel Lines and Transversals Example 3 – Use properties of parallel lines Find the value of x.

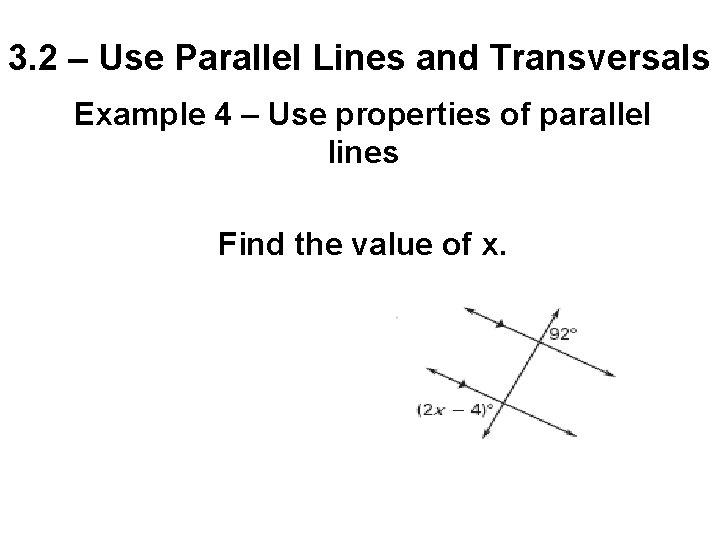
3. 2 – Use Parallel Lines and Transversals Example 4 – Use properties of parallel lines Find the value of x.

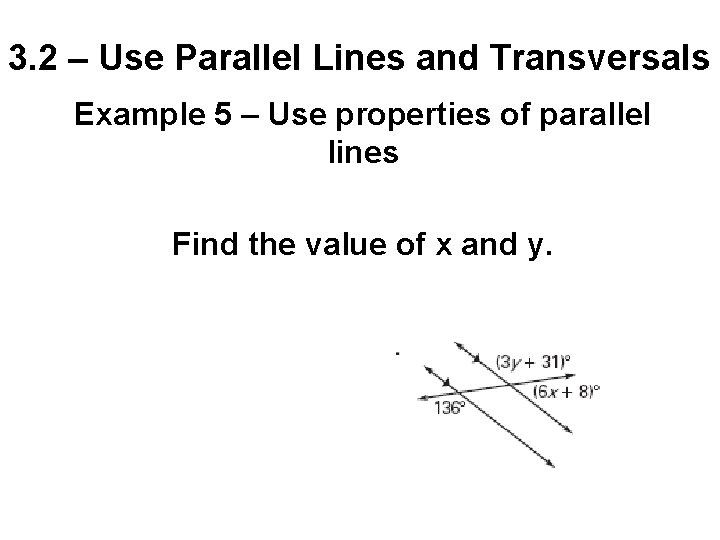
3. 2 – Use Parallel Lines and Transversals Example 5 – Use properties of parallel lines Find the value of x and y.

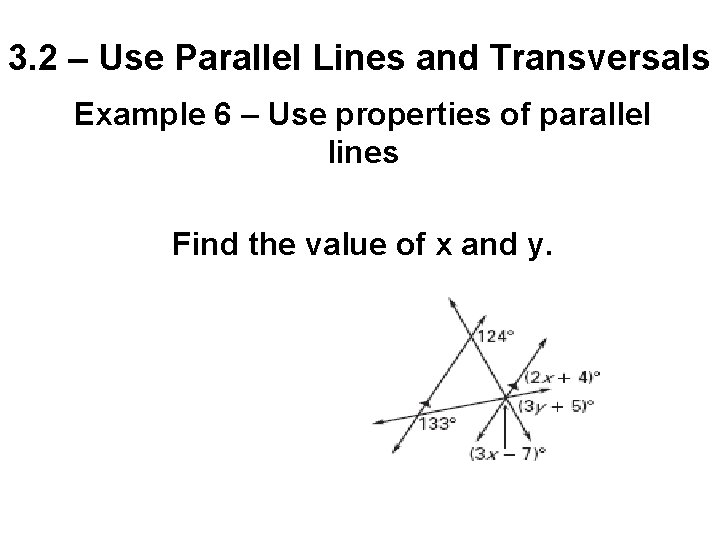
3. 2 – Use Parallel Lines and Transversals Example 6 – Use properties of parallel lines Find the value of x and y.

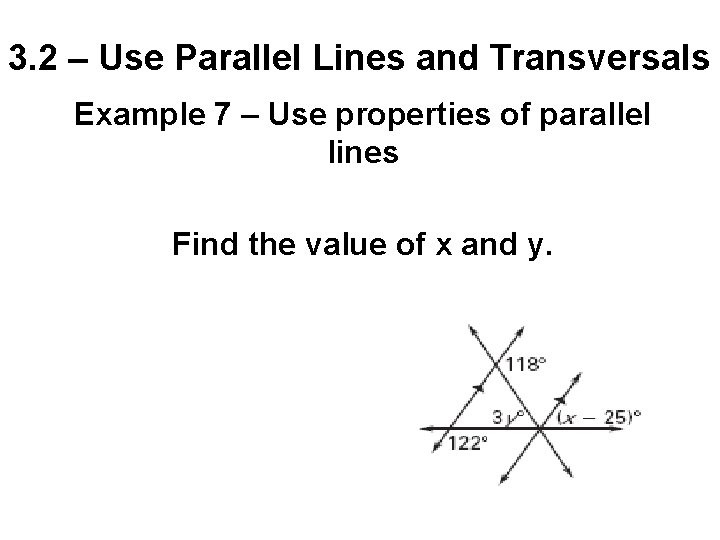
3. 2 – Use Parallel Lines and Transversals Example 7 – Use properties of parallel lines Find the value of x and y.

3. 2 – Use Parallel Lines and Transversals Example 8 – Prove the Alternate Interior Angles Theorem Prove that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.

3. 2 – Use Parallel Lines and Transversals Example 9 – Solve a real world problem. When sunlight enters a drop of rain, different colors of light leave the drop at different angles. This process is what makes a rainbow. For violet light, m<2 = 40 degrees. What is m<1? How do you know?