Optimization via too much Randomization Why parallelizing like

Optimization via (too much? ) Randomization Why parallelizing like crazy and being lazy can be good Peter Richtarik

Optimization as Mountain Climbing

Optimization with Big Data = Extreme* Mountain Climbing * in a billion dimensional space on a foggy day

Big Data BIG Volume BIG Velocity BIG Variety digital images & videos transaction records government records health records defence internet activity (social media, wikipedia, . . . ) • scientific measurements (physics, climate models, . . . ) • • •

God’s Algorithm = Teleportation

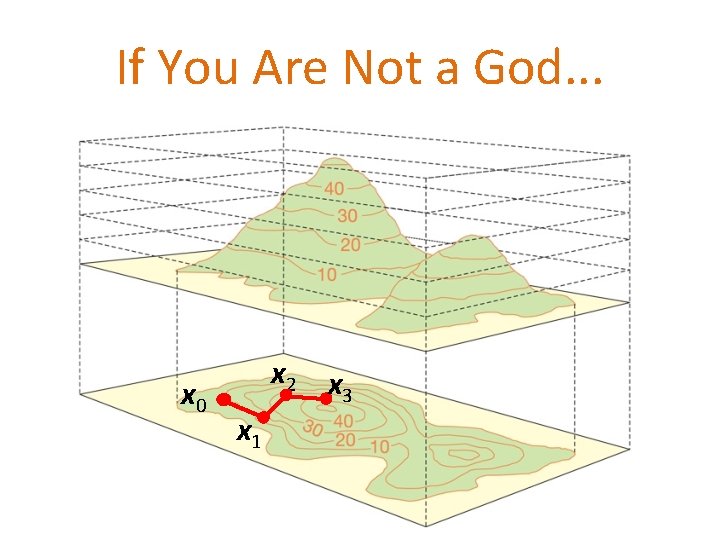
If You Are Not a God. . . x 0 x 2 x 3 x 1

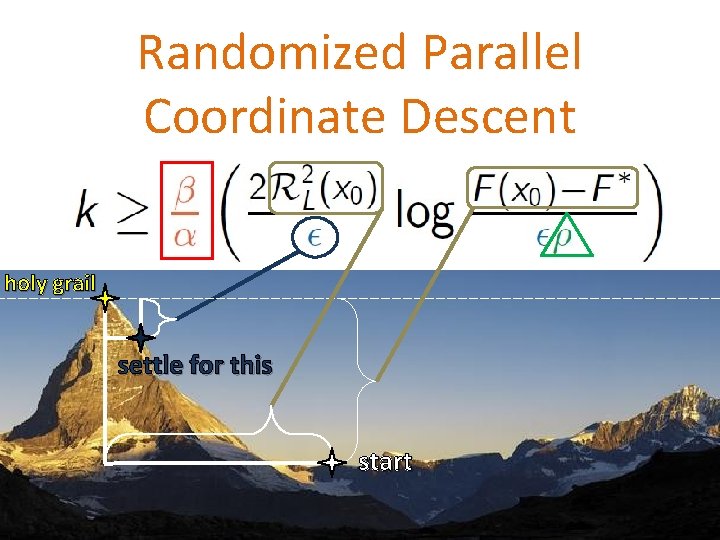
Randomized Parallel Coordinate Descent holy grail settle for this start

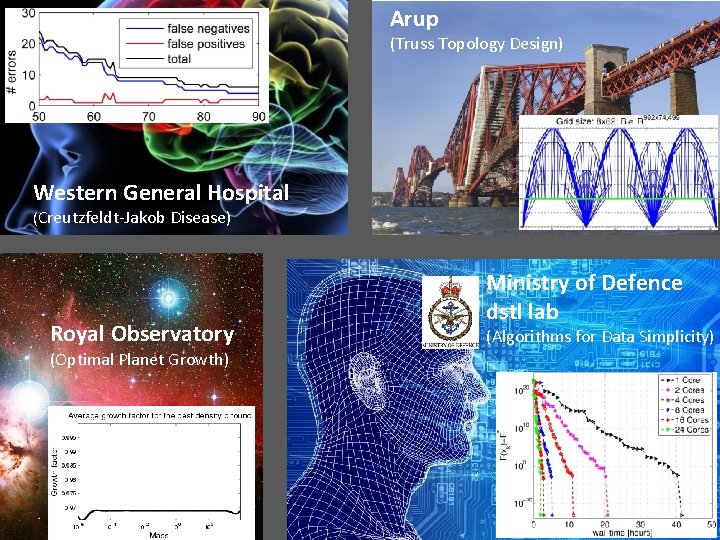
Arup (Truss Topology Design) Western General Hospital (Creutzfeldt-Jakob Disease) Royal Observatory (Optimal Planet Growth) Ministry of Defence dstl lab (Algorithms for Data Simplicity)

Optimization as Lock Breaking

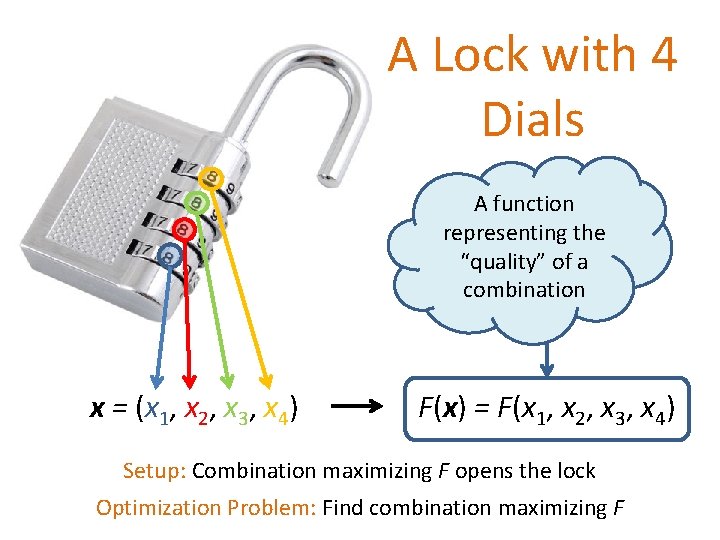
A Lock with 4 Dials A function representing the “quality” of a combination x = (x 1, x 2, x 3, x 4) F(x) = F(x 1, x 2, x 3, x 4) Setup: Combination maximizing F opens the lock Optimization Problem: Find combination maximizing F

Optimization Algorithm

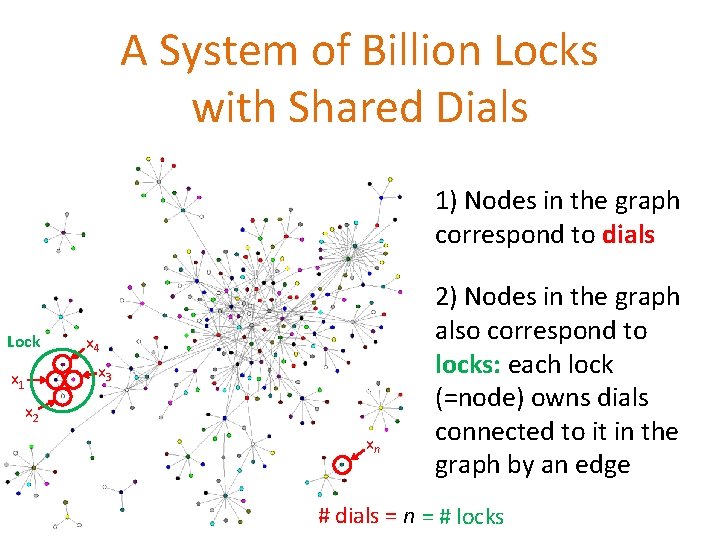
A System of Billion Locks with Shared Dials 1) Nodes in the graph correspond to dials Lock x 1 x 4 x 3 x 2 xn 2) Nodes in the graph also correspond to locks: each lock (=node) owns dials connected to it in the graph by an edge # dials = n = # locks

How do we Measure the Quality of a Combination? • Each lock j has its own quality function Fj depending on the dials it owns • However, it does NOT open when Fj is maximized • The system of locks opens when F = F 1 + F 2 +. . . + Fn is maximized F : Rn R

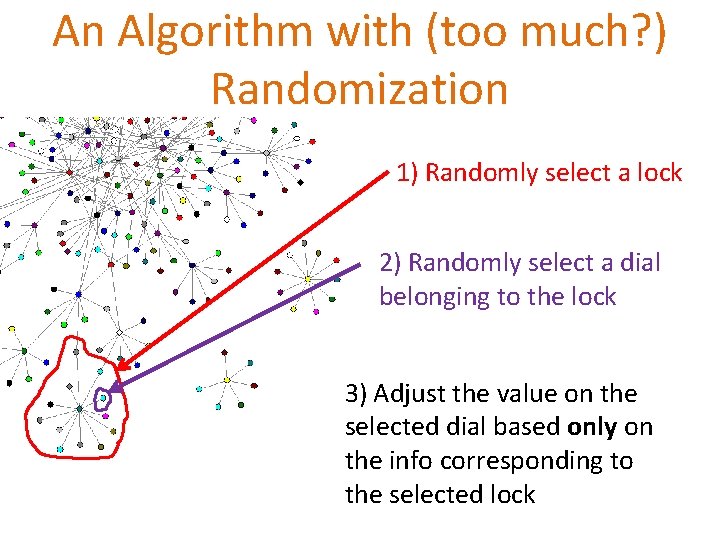
An Algorithm with (too much? ) Randomization 1) Randomly select a lock 2) Randomly select a dial belonging to the lock 3) Adjust the value on the selected dial based only on the info corresponding to the selected lock

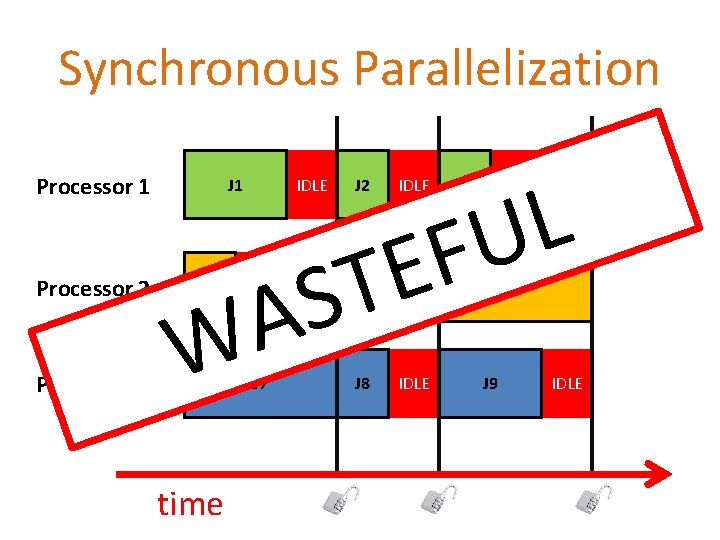
Synchronous Parallelization Processor 1 Processor 2 Processor 3 J 1 IDLE J 7 time IDLE E T S A W J 4 J 2 J 5 J 8 IDLE L FU J 3 IDLE J 6 J 9 IDLE

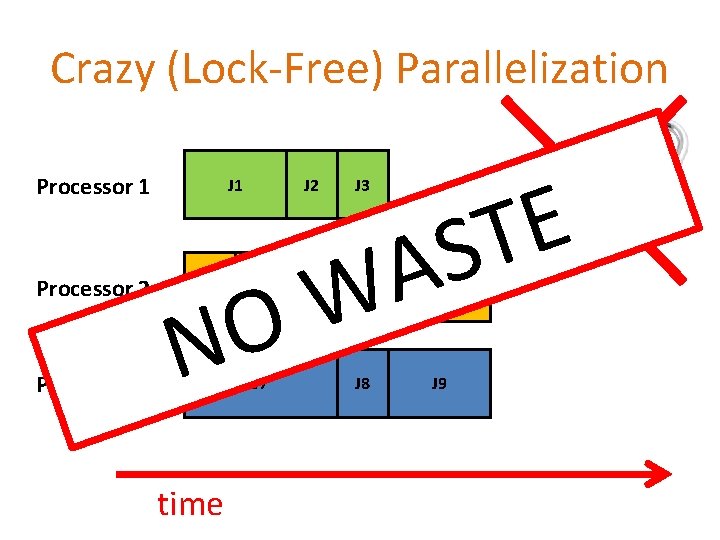
Crazy (Lock-Free) Parallelization Processor 1 Processor 2 Processor 3 J 1 J 4 J 3 W O N time J 2 J 5 J 7 J 8 E T S A J 6 J 9

Crazy Parallelization

Crazy Parallelization

Crazy Parallelization

Crazy Parallelization

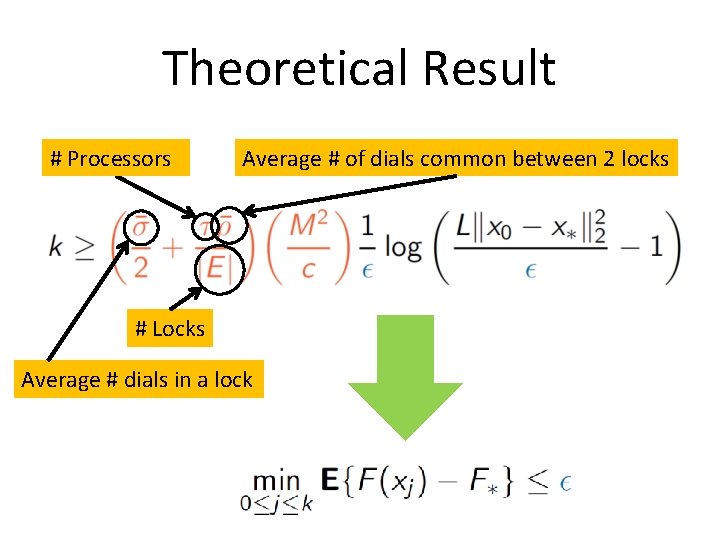
Theoretical Result # Processors Average # of dials common between 2 locks # Locks Average # dials in a lock

Computational Insights

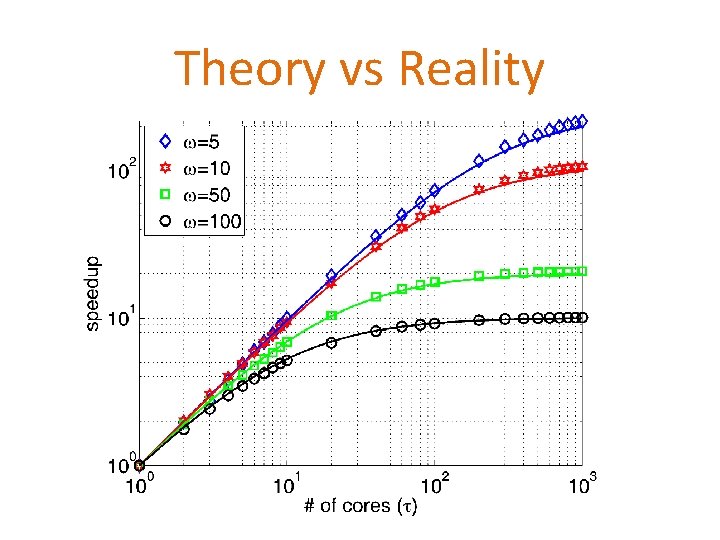
Theory vs Reality

Why parallelizing like crazy and being lazy can be good? Parallelization Randomization • • Effectivity Tractability Efficiency Scalability (big data) Parallelism Distribution Asynchronicity

Optimization Methods for Big Data • Randomized Coordinate Descent – P. R. and M. Takac: Parallel coordinate descent methods for big data optimization, Ar. Xiv: 1212. 0873 [can solve a problem with 1 billion variables in 2 hours using 24 processors] • Stochastic (Sub) Gradient Descent – P. R. and M. Takac: Randomized lock-free methods for minimizing partially separable convex functions [can be applied to optimize an unknown function] • Both of the above M. Takac, A. Bijral, P. R. and N. Srebro: Mini-batch primal and dual methods for support vector machines, Ar. Xiv: 1303. xxxx

Final 2 Slides

Probability HPC Matrix Theory Tools Machine Learning