Operacje zmiennoprzecinkowe Ernest Jamro Kat Elektroniki AGH Reprezentacja

Operacje zmiennoprzecinkowe Ernest Jamro Kat. Elektroniki AGH

Reprezentacja liczby IEEE-754 (32 -bity) (-1)Z x 2 e-127 x (1. m) Z. . . . wartość bitu znaku, E. . . wartość eksponenty, M. . . mantysa liczby Eksponenta (cecha)-8 bitów Mantysa (podstawa) – 23 bity Znak (mantysy) – 1 -bit IEEE-754 (64 -bity) Eksponenta (cecha)-11 bitów (-1)Z x 2 e-1023 x (1. m) Mantysa (podstawa) – 52 bity Znak (mantysy) – 1 -bit

Reprezentacja Mantysy Liczby ujemne mantysy są reprezentowana w formacie: znak, moduł Dwie postacie mantysy: Znormalizowana 1, m 1 m 2. . . m. N Zawsze 1 na najbardziej znaczącej pozycji Jedynka nie jest kodowana (jest ukryta) Nieznormalizowana 0, m 1 m 2. . . m. N Zero ukryte – domniema się zero dla eksponenty = 00. . 0 wtedy format liczby (-1)Z x 2 -b+1 x 0. m

Przykładowy, reprezentacja (32 -bity) znak eksponenta mantysa 1 bit 8 bits 23 bits 7/4 0 01111111 1 1 0 0 0 0 0 0 -34. 432175 1 10000100 0 0 0 1 1 1 0 1 0 0 0 1 1 0 0 -959818 1 1 0 0 1 0 1 1 0 1 0 1 0 0 0 +0 0 0000 0 0 0 0 0 0 -0 1 0000 0 0 0 0 0 0 +nieskończon. 0 1111 000000000000 najmniejsza 0 00000001 0 0 0 0 0 0 największa 0 11111110 1 1 1 1 1 1 -nieskonczon. 1 1111 000000000000 Na. N 0 1111 Chociaż jedna ‘ 1’ 2 -128** 0 0000 0100000000000

Operacje specjalne Na. N – not a number Operation n ÷ ± ± × ± ± ÷ 0 + + + (- + - ) ± 0 ÷ ± 0 + - + ± ÷ ± Result 0 ± ± + (- ) Na. N ± × 0 Na. N

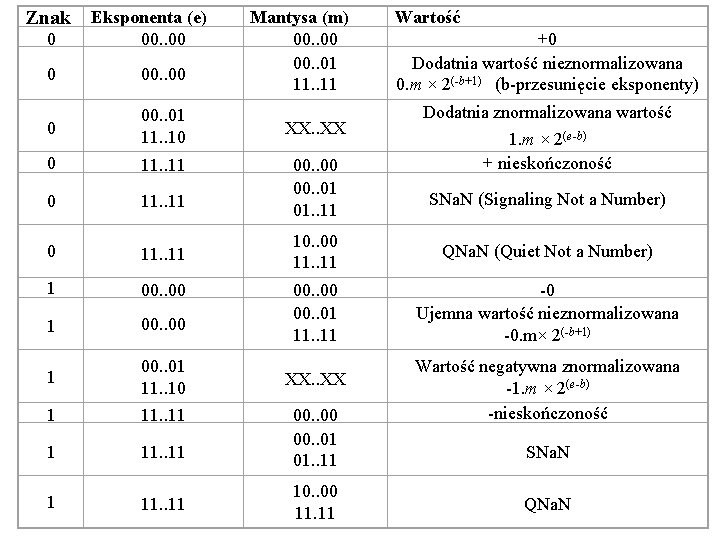
Znak Eksponenta (e) Mantysa (m) 00. . 00 00. . 01 11. . 11 Wartość 0 00. . 00 +0 Dodatnia wartość nieznormalizowana 0. m × 2(-b+1) (b-przesunięcie eksponenty) 0 00. . 00 0 00. . 01 11. . 10 XX. . XX 0 11. . 11 00. . 00 00. . 01 01. . 11 0 11. . 11 10. . 00 11. . 11 QNa. N (Quiet Not a Number) 1 00. . 00 00. . 01 11. . 11 -0 Ujemna wartość nieznormalizowana -0. m× 2(-b+1) 1 00. . 01 11. . 10 XX. . XX 1 11. . 11 00. . 00 00. . 01 01. . 11 Wartość negatywna znormalizowana -1. m × 2(e-b) -nieskończoność 1 11. . 11 10. . 00 11. 11 Dodatnia znormalizowana wartość 1. m × 2(e-b) + nieskończoność SNa. N (Signaling Not a Number) SNa. N QNa. N

Konwersja Integer->Float • Dokonać konwersji do formatu znak - moduł • Znaleźć najstarszą ‘ 1’ – w ten sposób określamy eksponentę • Dokonać przesunięcia tak aby najstarsza ‘ 1’ była na pozycji pierwszego bitu po kropce– w ten sposób określamy mantysę Algorytm sekwencyjny (wolny) - język C I- liczba wejściowa dodatnia (tylko moduł) if (I==0) { exp= 0; mantysa= 0; } // liczba zero int sh= 0; // przesunięcie while ( I & 0 x 8000000 == 0) // sprawdź najstarszy bit { sh++; I<<=1; } exp= 127+31 - sh; // eksponenta mantysa= I <<1; // mantysa zaczyna się od najstarszego bitu (pierwsza ‘ 1’ jest odrzucona)

Konwersja Integer->Float Algorytm szybki (zastosowany w sprzęcie) I- liczba wejściowa dodatnia (tylko moduł) int sh= 0; // przesunięcie if (I & 0 x. FFFF 0000 == 0) // sprawdź najstarsze 16 -bitów { I<<= 16; sh|= 0 x 10; } // ewentualnie przesuń o 16 bitów if (I & 0 x. FF 000000 == 0) // sprawdź najstarsze 8 bitów { I<<= 8; sh|= 8; } // ewentualnie przesuń o 8 bitów if (I & 0 x. F 0000000 == 0) // sprawdź najstarsze 4 bitów { I<<= 4; sh|= 4; } // ewentualnie przesuń o 4 bity if (I & 0 x. C 0000000 == 0) // sprawdź najstarsze 2 bitów { I<<= 2; sh|= 2; } // ewentualnie przesuń o 2 bitów if (I & 0 x 80000000 == 0) // sprawdź najstarszy bit { I<<= 1; sh|= 1; } // ewentualnie przesuń o 8 bitów if (I & 0 x 8000000 == 0) { exp= 0; mantysa= 0; } // liczba zero (sprawdź tylko najstarszy bit) else { mantysa= I<<1; exp= 31+127 -sh; }

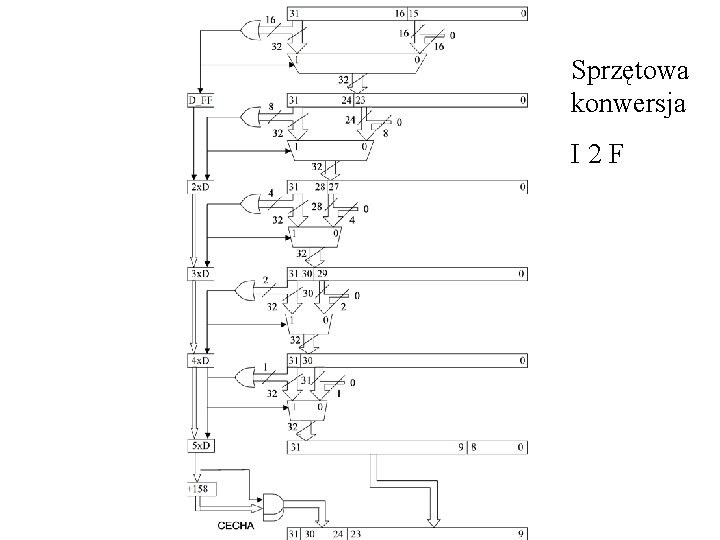
Sprzętowa konwersja I 2 F

Konwersja Float -> Int I= (1<<sizeof(Mantysa) | M; // dołożenie 1 na najstarszym bicie I<<= Eksponenta – 127 – sizeof(Mantysa) Uwaga wspomniana konwersja nie może być w prosty sposób wykonana dla formatu int 32 oraz float 64

Operacja mnożenia i dzielenia Mnożenie: Y= A*B= ((-1)Sa * MA*2 Ea-b) * ((-1)Sb * MB * 2 Eb-b) Y= (-1)Sa+Sb * MA*MB * 2 Ea+Eb– 2 b (b – przesuniecie eksponenty) SY= SA xor SB MY= MA * MB (należy pamiętać o wiodących jedynkach. W niektórych przypadkach MY >=2. 0 co wymaga dodatkowego przesunięcia o jeden bit w prawo) EY= EA + EB – b (+1 – w przypadku dodatkowej normalizacji) Dzielenie Y= A/B = ((-1)Sa * MA*2 Ea-b) / ((-1)Sb * MB * 2 Eb-b Y= (-1)Sa+Sb * (MA/MB) * 2 Ea – Eb SY= SA xor SB MY= MA / MB – uwaga mantysa wymaga normalizacji (przesunięcia w lewo o kbitów) EY= EA – EB + b – k (k przesunięcia mantysy o k-bitów podczas normalizacji)

Operacja dodawania Założenie EA >= EB (w przeciwnym wypadku zamienić argumenty) Y= A+B= ((-1)Sa * MA*2 Ea-b) + ((-1)Sb * MB * 2 Eb-b Y= (-1)Sa * (MA + ((-1)Sb+Sa MB)>>(EA-EB) ) * 2 Ea-b Wykonywanie operacje: Porównanie EA i EB i ewentualne zamienienie argumentów Przesunięcia MB o (EA-EB) bitów w prawo Wykonanie operacji dodawania (lub odejmowania jeżeli SA SB). Normalizacja wyniku Operacja odejmowania: Wystarczy zanegować znak SB Zobacz: http: //tima-cmp. imag. fr/~guyot/Cours/Oparithm/english/Flottan. htm

Propagacja błędów Operacja dodawania AR= A + e. R; AR – rzeczywista wartość A, A- wartość otrzymana AR + BR = A + e. A + B + e. B (e. A- błąd reprezentacji liczby AR) AR + BR = (A+B) + e. A + e. B e. AB= (AR + BR) – (A+B) = e. A + e. B propagacja błędu bezwzględnego, błąd ma szczególne znaczenie w przypadku kiedy (A+B) dużo mniejsze od A i B. Najgorszy przypadek wtedy kiedy A -B wtedy możliwe jest że e. AB AR+BR Operacja mnożenia AR * BR = (A + e. A) * (B + e. B)= A*B + A*e. B + B*e. A + (e. A*e. B – można pominąć) Następuje propagacja i sumowanie błędów (szczególne znaczenie ma błąd reprezentacji liczby mniejszej), natomiast nie następuje zwielokrotnienie błędu jak to może mieć miejsce w przypadku operacji dodawania

Zalety i wady reprezentacji zmiennoprzecinkowej Operacje zmiennoprzecinkowe są zalecane tam gdzie wartości liczb mają bardzo różne wielkości (różne eksponenty). Część znaczących bitów reprezentacji zmiennoprzecinkowej jest tracona na eksponentę, np. dla 32 -bitowej reprezentacji jest to 8 -bitów. Dlatego jeżeli liczby wejściowe nie różnią się o więcej niż o 8 bitów w eksponencie zaleca się stosować reprezentację stałoprzecinkową, w której każda liczba jest reprezentowana na 32 bitach. Zaletą liczb zmiennoprzecinkowych jest to, że błąd względny reprezentacji jest stały. Wada – operacje zmiennoprzecinkowe są bardziej skomplikowane i przez to zajmują więcej zasobów i są z reguły wolniej wykonywane. Ma to szczególne znaczenie w przypadku operacji dodawania.

Operacje stałoprzecinkowe Bardzo często nie jest konieczne stosowanie operacji zmiennoprzecinkowych – można je zastąpić operacjami stałoprzecinkowymi czyli pośrednio operacjami na liczbach całkowitych Często wynik operacji stałoprzecinkowych jest szybszy i dokładniejszy od wyniku operacji zmiennoprzecinkowych ponieważ nie jest tracona informacja na eksponentę Reprezentacja stałoprzecinkowa AR= A << EA AR- liczba rzeczywista, A- liczba całkowita, EA- stałe przesunięcie dla wszystkich operacji. Przesunięcie EA nie jest uwzględniane podczas obliczeń a jedynie na samym początku i końcu obliczeń. Przykład: Y= A 1*B 1 + A 2*B 2 + C 3*B 3 Ai= Ari << EA; Bi= Bri << EB YR= Y >> (EA + EB) Wada: Konieczność pamiętania przesunięcia każdej operacji. Możliwość stosowania tylko wtedy kiedy przesunięcia EAi oraz EBi są podobnej wartość (nie różnią się o więcej niż około 10 bitów)

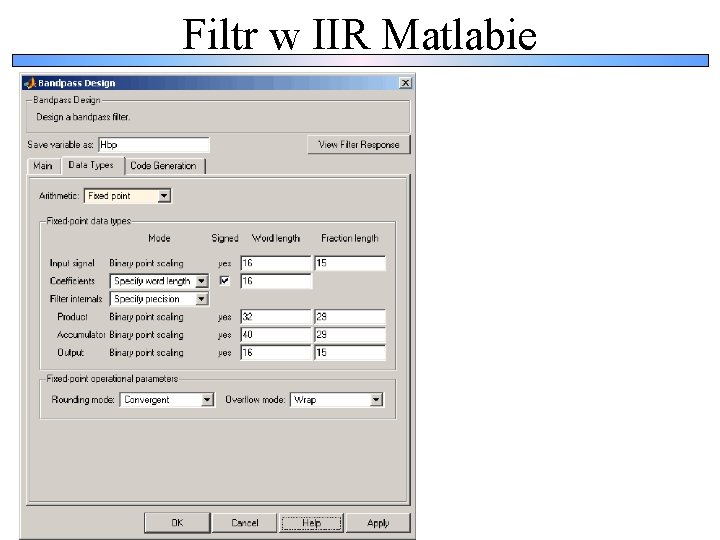
Filtr w IIR Matlabie

Rounding Modes Sets the mode the filter uses to quantize numeric values when the values lie between representable values for the data format (word and fraction lengths). • ceil - Round toward positive infinity. • convergent - Round to the closest representable integer. Ties round to the nearest even stored integer. This is the least biased of the methods available in this software. E. g. 101. 1000 110; 1000 100 ale 1001 101 • round - Round toward nearest. Ties round toward negative infinity for negative numbers, and toward positive infinity for positive numbers. • zero/fix - Round toward zero. • floor - Round toward negative infinity. • nearest - Round toward nearest. Ties round toward positive infinity.