On Constructing Parallel Pseudorandom Generators from OneWay Functions

On Constructing Parallel Pseudorandom Generators from One-Way Functions Emanuele Viola Harvard University June 2005

Pseudorandom Generator (PRG) [BM, Y] PRG • Poly(n)-time Computable • Stretch s(n) ¸ 1 (e. g. , s(n) = 1, s(n) = n) • Fools efficient adversaries: 8 PPT A Pr. X, |X| = n+s(n)[A(X) = 1] ¼ Pr , | | = n [A(PRG( )) = 1]

Background on PRG • PRG , One-Way Functions (OWF) [BM, Y, GL, …, HILL] (f OWF if easy to compute but hard to invert, i. e. 8 PPT M, almost never M(f(X)) 2 f(X)-1) • Applications of PRG: cryptography, derandomization need stretch s(n) = poly(n) • Stretch s(n) only makes sense relative to n 2 n {0, 1} – E. g. G : ! )G: – Two main cases s(n) = 1, or s(n) = n {0, 1}n+s(n) ! 2 + n¢s(n) n {0, 1}

PRG Constructions • We study complexity of constructing PRG with big stretch from OWF f • Def. : black-box PRG constructions Gf : for every (comput. -unbounded) function f, adversary A A breaks Gf ) 9 PPT M : Mf, A inverts f • Most constructions are black-box [BM, Y, …, HILL] Many negat. results for black-box model [IR, …, GT, RTV] – Cannot make sense of negat. result in non-black-box model

Standard Constructions w/ big stretch • STEP 1: OWF f ) Gf : {0, 1}n ! {0, 1}n+1 n – Think e. g. f : {0, 1} ! {0, 1} Gf n • STEP 2: Gf ) PRG with stretch s(n) = poly(n) [GM] Input Gf Gf Gf … . . . . Output. . • Stretch s ) s adaptive queries to f ) circuit depth ¸ s • Question [this work]: stretch s vs. adaptivity & depth? E. g. , can have s = n, circuit depth O(log n)?

Previous Results • [AIK] Log-depth OWF/PRG ) O(1)-depth PRG (!!!) However, any stretch ) stretch s = 1 • [GT] s vs. number q of queries to OWF (Thm: q ¸ s) [This work] s vs. adaptivity & circuit depth • […, IN, NR] O(1)-depth PRG from specific assumptions [This work] general assumptions • Context: [V] studies complexity of NW-type PRG

Outline • Our model • Our results • Proof sketch of main negative result • Other: new negative result on worst-case vs. average-case connections in NP, PH

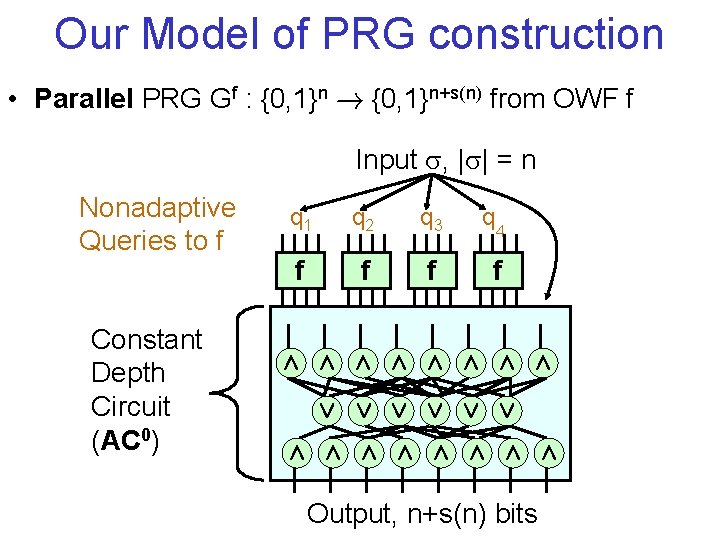
Our Model of PRG construction • Parallel PRG Gf : {0, 1}n ! {0, 1}n+s(n) from OWF f Input , | | = n Nonadaptive Queries to f Constant Depth Circuit (AC 0) q 1 q 2 q 3 q 4 f f Æ Æ Æ Æ Ç Ç Ç Æ Æ Æ Æ Output, n+s(n) bits

Our Results on PRG Constructions • Parallel construction Gf : {0, 1}n ! {0, 1}n+s(n) n n From one-way function f ( e. g. f : {0, 1} ! {0, 1} ) f arbitrary f one-to-one f permutation Neg. s(n) · o(n) ? Pos. ? s(n) ¸ 1

Proof Sketch of Negative Result • Thm[this work]: Parallel black-box PRG constructions Gf : {0, 1}n ! {0, 1}n+s(n) satisfy s(n) · o(n) • Proof: Exhibit comput. -unbounded f, A such that: (1) A breaks Gf when s(n) = (n) (2) f one-way, i. e. hard to invert. We show distribution on f s. t. (1) & (2) hold w. h. p.

Def. of f and (1) break Gf • Restriction [FSS, H, …] maps bits to {0, 1, *} • Def. distribution on f apply to truth-table of f f(0) f(111) 01** 1*0* 1**0 0101 1100 1110 – known to adversary A replace * with random bits (1) A breaks Gf : 0 f 8 , G ( ) is AC function of truth-table of f ) makes Gf( ) biased ) A breaks Gf( ). – If s(n) = (n) can union bound over all .

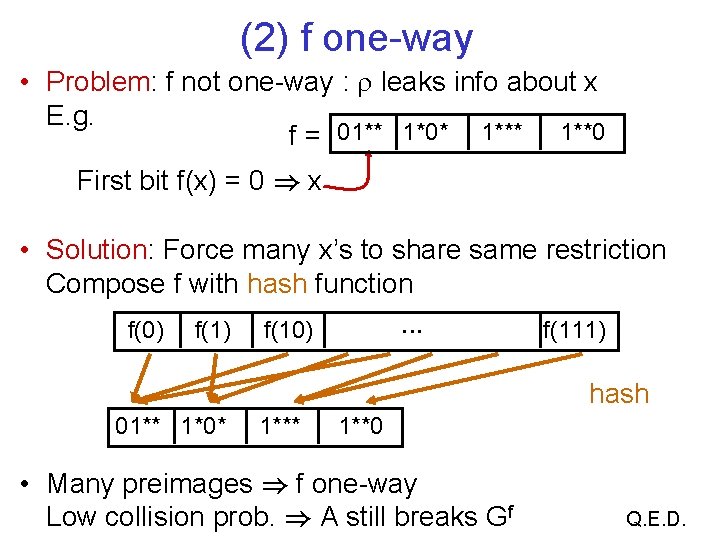
(2) f one-way • Problem: f not one-way : leaks info about x E. g. f = 01** 1*0* 1**0 First bit f(x) = 0 ) x • Solution: Force many x’s to share same restriction Compose f with hash function f(0) f(10) f(111) hash 01** 1*0* 1**0 • Many preimages ) f one-way Low collision prob. ) A still breaks Gf Q. E. D.

Our Result on Average Case Complexity • Question: given f 2 NP worst-case hard (f 2 P/poly), can build f 0 2 NP average-case hard? I. e. 8 small circuit A : Prx[A(x) f 0(x)] ¸ 1/3 • Thm[V]: no black-box construction of f 0 using both function f and adversary A as black-box • Thm[BT]: no construction using A as black-box – Also uses A ``non-adaptively’’ • Thm[this work]: no construction using f as black-box – Proof uses pseudorandom restrictions

Conclusion • Thm[this work]: Parallel black-box construction Gf : {0, 1}n ! {0, 1}n+s(n) satisfy f arbitrary f one-to-one f permutation Neg. s(n) · o(n) ? Pos. ? s(n) ¸ 1 • Average-case complexity Thm[this work]: given f 2 NP worst-case hard no construction of average-case hard f 0 2 NP using f as black-box

Pseudorandom Bits for Constant-Depth Circuits with Few Arbitrary Symmetric Gates Emanuele Viola Harvard University April 2005

Pseudorandom Generator (PRG) [BM, Y, NW] PRG • Efficiently Computable • Big Stretch s(n) À n ( e. g. s(n) = n (1) ) • Fools small circuits: 8 small C Pr. X, |X| = s(n)[C(X) = 1] ¼ Pr , | | = n [C(PRG( )) = 1]

Do PRG Exist? • PRG ) derandomization: BP ¢ P ( EXP [Y, NW, …] • PRG , circuit lower bounds: EXP P/poly [NW, BFNW, STV, SU, …] • Open Problem: PRG exist? • This Work: study restricted PRG Only fool constant-depth circuits We know lower bounds for constant-depth circuits

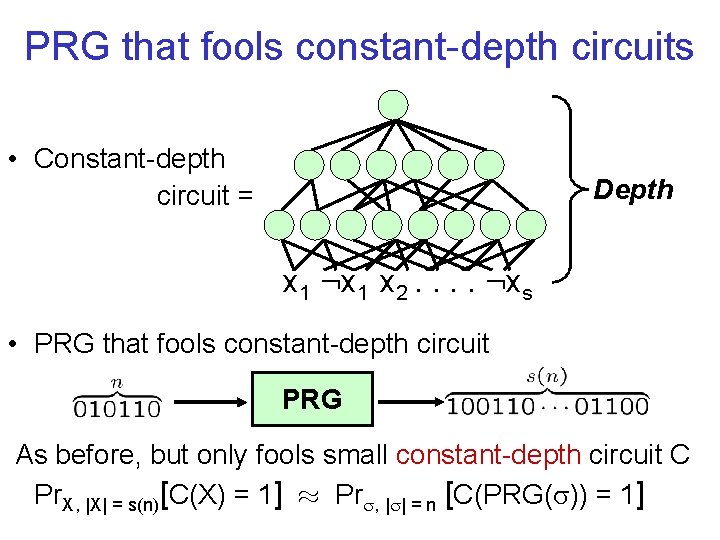
PRG that fools constant-depth circuits • Constant-depth circuit = Depth x 1 : x 1 x 2. . : xs • PRG that fools constant-depth circuit PRG As before, but only fools small constant-depth circuit C Pr. X, |X| = s(n)[C(X) = 1] ¼ Pr , | | = n [C(PRG( )) = 1]

Previous Results Æ • [N’ 91] PRG : {0, 1}n ! {0, 1}s(n) = n 2 , fools AC 0 Ç Ç Ç = Æ Æ Æ Æ x 1 : x 1 x 2. . . : xs • Applications: BP ¢ AC 0 ( EXP, more in [NW, HVV, V] • [LVW’ 93] PRG : {0, 1}n ! {0, 1}s(n) SYM s(n) = n log n, fools SYM ○ AND = Æ Æ Æ SYM = arbitrary symmetric gate x 1 : x 1 x 2. . : xs E. g. , SYM = PARITY, MAJORITY

Our Results • Theorem[This Work]: {0, 1}n {0, 1}s(n) PRG : ! with s(n) = n log n fools AC 0 with log 2 n SYM = SYM Ç Ç SYM Æ Æ Æ Æ x 1 : x 1 x 2. . : xs • Improves on [LVW 93] Fools richer class than [N 91] but worse stretch • BP ¢ (AC 0 with few SYM) ( EXP Currently richest BP ¢ class one can derandomize

The Pseudorandom Generator • [NW] style Input = 110101110110101110 f Output = 101010 …. . . . 1 ………. . . 1010100 © f= [RW] Æ Æ © © x 1. . . xn © = PARITY

Outline • Why previous results/techniques do not suffice • For PRG need new average-case lower bound for AC 0 with few SYM • Proof sketch of average-case lower bound

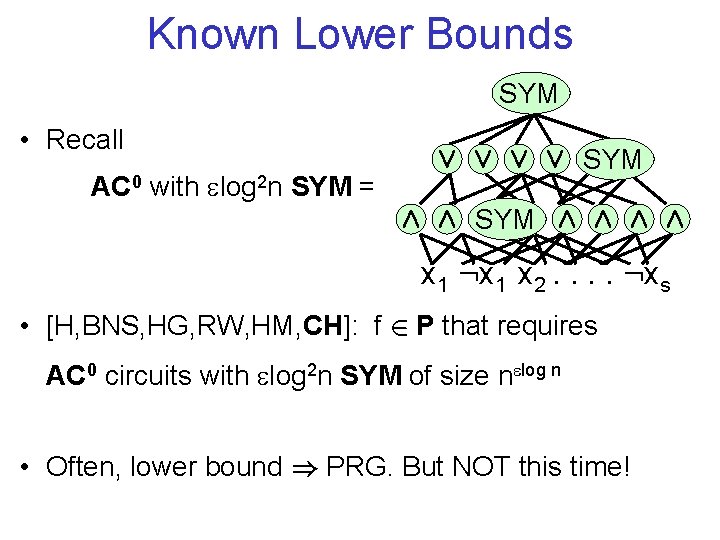
Known Lower Bounds SYM • Recall AC 0 with log 2 n SYM = Ç Ç SYM Æ Æ Æ Æ x 1 : x 1 x 2. . : xs • [H, BNS, HG, RW, HM, CH]: f 2 P that requires AC 0 circuits with log 2 n SYM of size n log n • Often, lower bound ) PRG. But NOT this time!

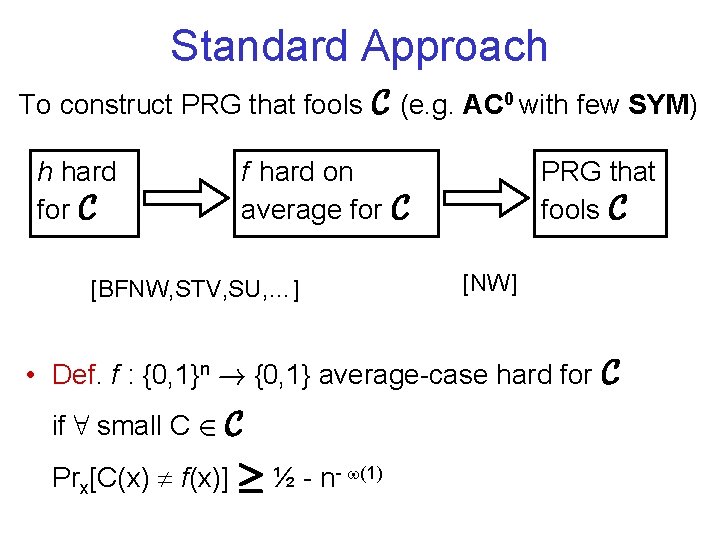
Standard Approach To construct PRG that fools C (e. g. AC 0 with few SYM) h hard for C f hard on average for C [BFNW, STV, SU, …] PRG that fools C [NW] • Def. f : {0, 1}n ! {0, 1} average-case hard for C if 8 small C 2 C Prx[C(x) f(x)] ¸ ½ - n- (1)

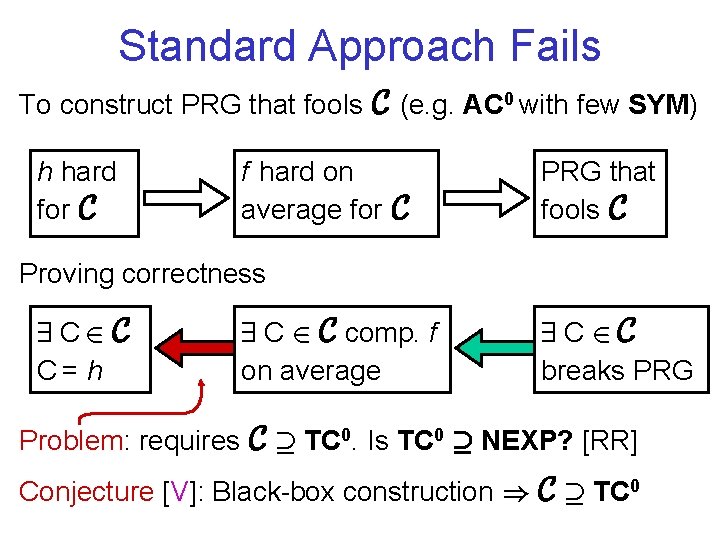
Standard Approach Fails To construct PRG that fools C (e. g. AC 0 with few SYM) h hard for C f hard on average for C PRG that fools C Proving correctness 9 C 2 C C= h 9 C 2 C comp. f on average 9 C 2 C breaks PRG Problem: requires C ¶ TC 0. Is TC 0 ¶ NEXP? [RR] Conjecture [V]: Black-box construction ) C ¶ TC 0

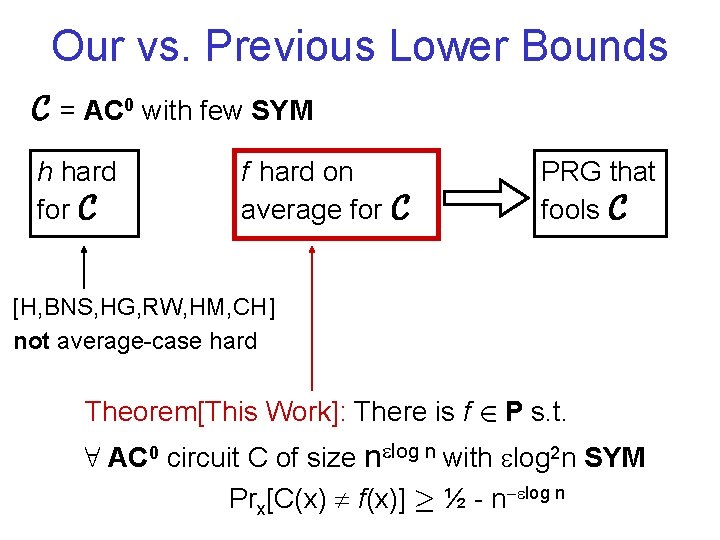
Our vs. Previous Lower Bounds C = AC 0 with few SYM h hard for C f hard on average for C PRG that fools C [H, BNS, HG, RW, HM, CH] not average-case hard Theorem[This Work]: There is f 2 P s. t. 8 AC 0 circuit C of size n log n with log 2 n SYM Prx[C(x) f(x)] ¸ ½ - n- log n

Tools • Random restrictions [FSS, H, …] : {x 1, x 2, …, xs} ! {0, 1, *} C| subcircuit on *’s • Multiparty communication complexity [CFL] © Thm[BNS]: Gen. Inner Product (GIP) = Æ Æ has high x 1. . . . xn communication complexity

Proof Sketch © • Thm[This Work]: f = GIP ○ PARITY = Æ Æ is average-case hard for © © small AC 0 circuits with few SYM x 1. . . . xn • Proof sketch: C small AC 0 circuit with few SYM. W. h. p. over random restriction : E 1: GIP ○ PARITY| ¼ GIP ) high comm. complexity E 1 ( each bottom PARITY has * E 2: C| computable with low comm. complexity E 1 and E 2 ) C| (x) GIP(x) Q. E. D.

Conclusion • Theorem[This Work]: PRG : {0, 1}n ! {0, 1}s(n) with s(n) = n log n fools AC 0 with log 2 n SYM • Improves [LVW 93], fools richer class than [N 91] Currently richest BP ¢ class one can derandomize • Obtained from average-case hardness result Conj. : PRG from worst-case hardness ) C ¶ TC 0 • Open problems: (log 2 n) SYM? EXP average-case hard for GF(2) poly of deg. log n ?

C| low communication complexity • Lemma[this work]: C small AC 0 circuit w/ log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Lemma[HG+HM]: Above holds for 1 SYM

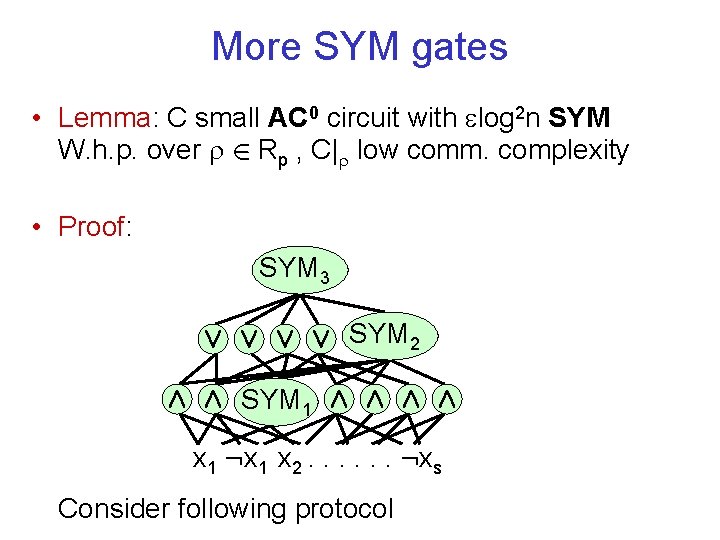
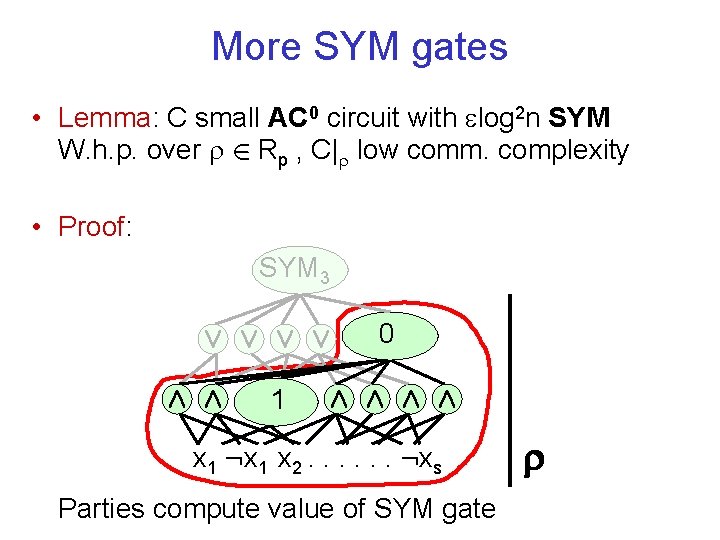
More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: SYM 3 Ç Ç SYM 2 Æ Æ SYM 1 Æ Æ x 1 : x 1 x 2. . . : xs Consider following protocol

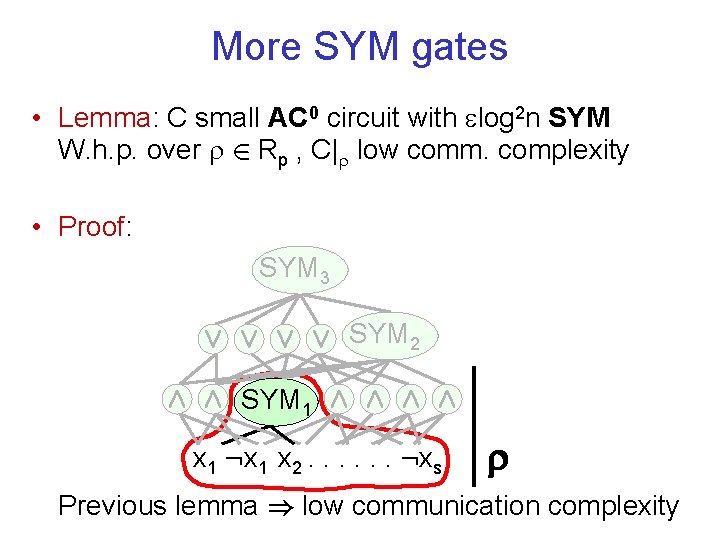
More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: SYM 3 Ç Ç SYM 2 Æ Æ SYM 1 Æ Æ x 1 : x 1 x 2. . . : xs Previous lemma ) low communication complexity

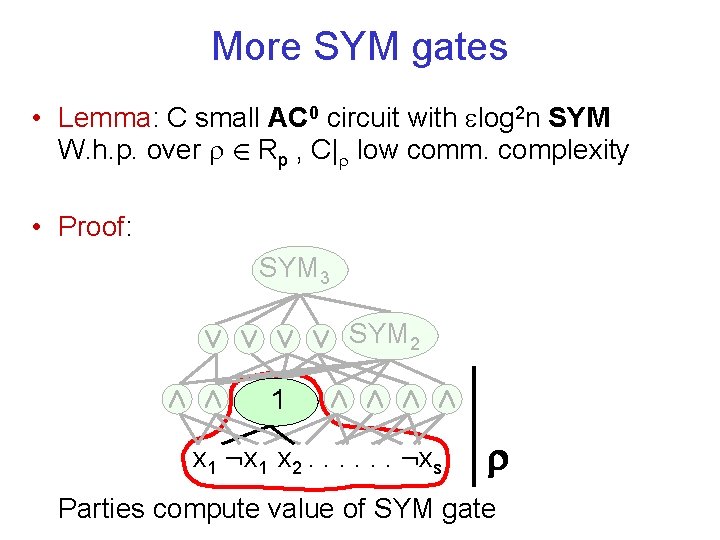
More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: SYM 3 Ç Ç SYM 2 Æ Æ 1 Æ Æ x 1 : x 1 x 2. . . : xs Parties compute value of SYM gate

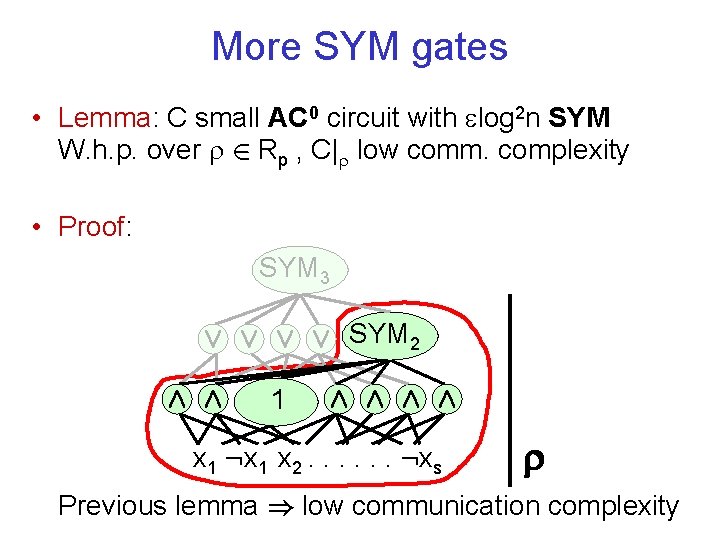
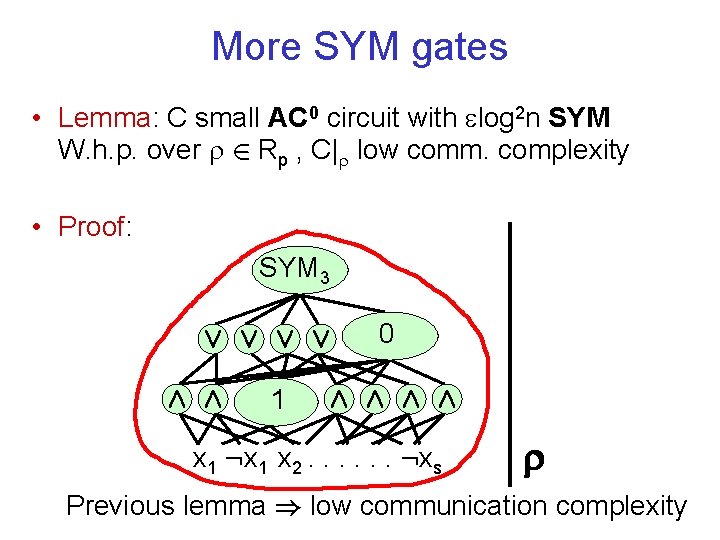
More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: SYM 3 Ç Ç SYM 2 Æ Æ 1 Æ Æ x 1 : x 1 x 2. . . : xs Previous lemma ) low communication complexity

More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: SYM 3 Ç Ç Æ Æ 1 0 Æ Æ x 1 : x 1 x 2. . . : xs Parties compute value of SYM gate

More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: SYM 3 Ç Ç Æ Æ 1 0 Æ Æ x 1 : x 1 x 2. . . : xs Previous lemma ) low communication complexity

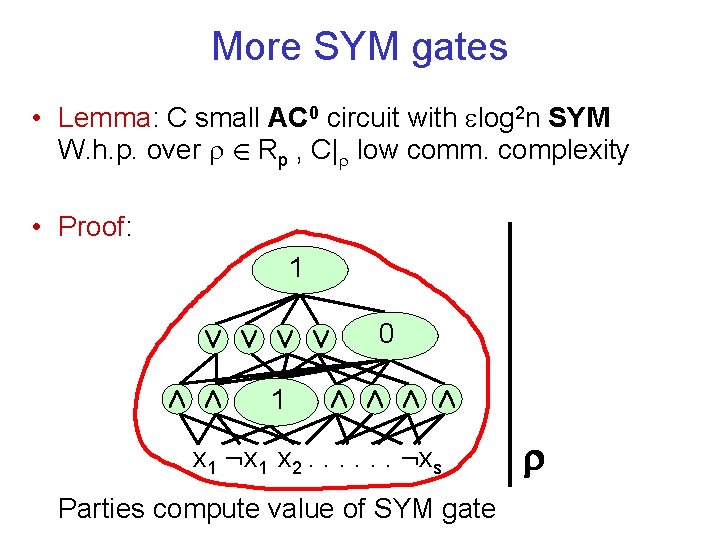
More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: 1 Ç Ç Æ Æ 1 0 Æ Æ x 1 : x 1 x 2. . . : xs Parties compute value of SYM gate

More SYM gates • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: Total communication = communication for 1 SYM X number of SYM Q. E. D. • Union bound over 2#SYM circuits limits # SYM. Open Problem: Better analysis?

Conclusion • Theorem[This Work]: PRG : {0, 1}n ! {0, 1}s(n) with s(n) = n log n fools AC 0 with log 2 n SYM • Improves [LVW 93], fools richer class than [N 91] Currently richest BP ¢ class one can derandomize • Obtained from average-case hardness result Conj. : PRG from worst-case hardness ) C ¶ TC 0 • Open problems: (log 2 n) SYM? EXP average-case hard for GF(2) poly of deg. log n ?

Multiparty Communication Complexity • ``Number on the forehead’’ model [CFL] – – • • k-parties want to compute f(x) x partitioned in k blocks ! x 1 i-th party knows all x but xi Communication = broadcast x 2 xk Generalized Inner Product. GIP(x) = Æ © n k Æ k x 1. . xnk Lemma[BNS]: Low communication complexity protocol P ) Prx[P(x) GIP(x)] ¸ ½ - n- log n – Discrepancy, [CT, R]

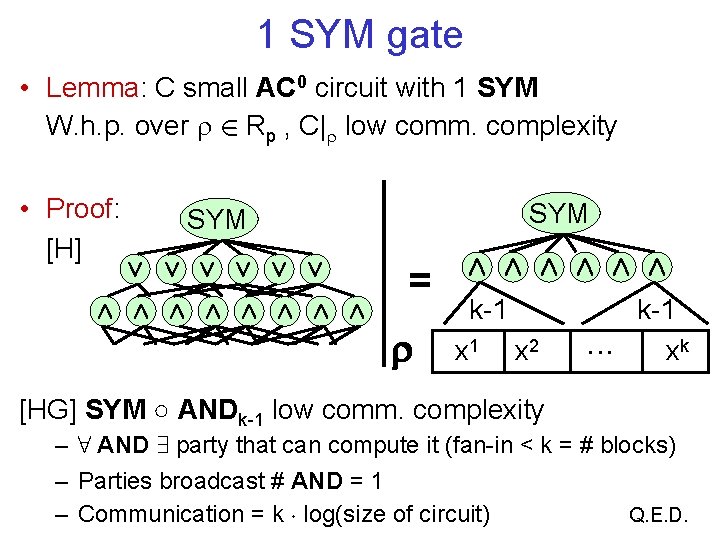
C| low communication complexity • Restriction [FSS, …] map variables to {0, 1, *} – Rp = uniform distribution, Pr[ (xi) = *] = p – C| subcircuit. New input bits = * • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • First prove 1 SYM, then log 2 n SYM

1 SYM gate • Lemma: C small AC 0 circuit with 1 SYM W. h. p. over 2 Rp , C| low comm. complexity • Proof: [H] SYM Ç Ç Ç Æ Æ Æ Æ = Æ Æ Æ k-1 x 2 k-1 xk [HG] SYM ○ ANDk-1 low comm. complexity – 8 AND 9 party that can compute it (fan-in < k = # blocks) – Parties broadcast # AND = 1 – Communication = k ¢ log(size of circuit) Q. E. D.

Summary of Lemmas • Lemma[BNS]: Low communication complexity protocol P ) Prx[P(x) GIP(x)] ¸ ½ - n- log n • Lemma: C small AC 0 circuit with log 2 n SYM W. h. p. over 2 Rp , C| low comm. complexity • Want Theorem: There is f 2 P s. t. 8 AC 0 circuit C of size n log n with log 2 n SYM gates Prx[C(x) f(x)] ¸ ½ - n- log n

© Proof: f = GIP ○ PARITY = Æ Æ © © x 1. . . . xn C small AC 0 circuit with log 2 n SYM Random Input x = random + random y for the * • E 1: f | ¼ GIP ) high comm. complexity – E 1 ( each bottom PARITY has * • E 2: C| low comm. complexity Prx[C(x) f (x)] ¸ Pr , y[C| (y) f| (y) | E 1, E 2] Pr[E 1, E 2] = Pry[P(y) GIP(y)] (1 - n- log n) ¸ ( ½ - n- log n)

Conclusion • Theorem[This Work]: PRG : {0, 1}n ! {0, 1}s(n) with s(n) = n log n fools AC 0 with log 2 n SYM • Improves [LVW 93], fools richer class than [N 91] Currently richest BP ¢ class one can derandomize • Obtained from average-case hard function Conj. : PRG from worst-case hardness ) EXP TC 0 • Open problems: (log 2 n) SYM? EXP average-case hard for GF(2) poly of deg. log n ?

Proof Sketch • Tools: Random restrictions [FSS, H, …] – : {x 1, x 2, …, xs} ! {0, 1, *} , C| subcircuit on *’s Communication complexity bound for GIP [BNS] • Theorem[This Work]: GIP ○ PARITY is average-case hard for small AC 0 circuits with few SYM • Proof sketch: C small AC 0 circuit with few SYM. W. h. p. over random restriction : E 1: GIP ○ PARITY| ¼ GIP ) high comm. complexity E 2: C| computable with low comm. complexity E 1 and E 2 ) C| (x) GIP(x) Q. E. D.