Pseudorandom Generators for Polynomial Threshold Functions Raghu Meka










![Fooling Majority Let Partition [n] into t blocks. Block 1 Block t Observe: �Y’s Fooling Majority Let Partition [n] into t blocks. Block 1 Block t Observe: �Y’s](https://slidetodoc.com/presentation_image_h/aff67132a3ddf2d88c825a4e92041118/image-13.jpg)








![Subsequent Work 30 Reference Gopalan et al. [GOWZ 09] Harsha et al. [HKM 09 Subsequent Work 30 Reference Gopalan et al. [GOWZ 09] Harsha et al. [HKM 09](https://slidetodoc.com/presentation_image_h/aff67132a3ddf2d88c825a4e92041118/image-30.jpg)





- Slides: 35

Pseudorandom Generators for Polynomial Threshold Functions Raghu Meka UT Austin (joint work with David Zuckerman) 1

Polynomial Threshold Functions Applications: Complexity theory, learning theory, voting theory, quantum computing 2

Halfspaces Applications: Perceptrons, Boosting, Support Vector Machines 3

Good PRGs for Important PTFs? in Complexity theory. This Work Algorithmic applications: explicit Johnson-Lindenstrauss families, > 1. First nontrivial answer for degrees derandomizing Goemans. Significant improvements for degree 1. Williamson. Generic techniques: PRGs from CLTs, monotone trick. 4

PRGs for PTFs Small set preserving fraction of +’ve points for all PTFs Fraction of set Positive Universe Small Universe ofof. PRG Points points ~ Fraction of Positive PRG points 5

PRGs for PTFs Stretch r bits to n bits and fool degree d PTFs. 6

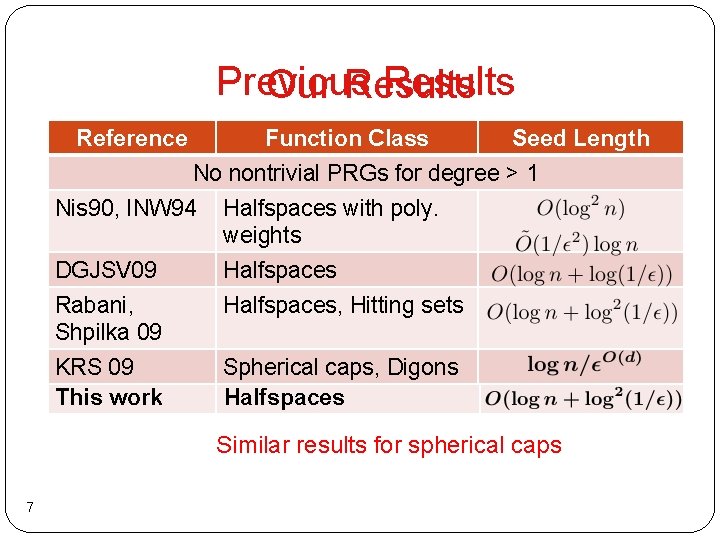
Previous Results Our Results Reference Function Class Seed Length No nontrivial PRGs for degree > 1 Nis 90, INW 94 Halfspaces with poly. weights DGJSV 09 Halfspaces Rabani, Shpilka 09 This 09 work KRS Halfspaces, Hitting sets This work Degree d caps, PTFs Digons Spherical Halfspaces Similar results for spherical caps 7

Independent Work Ø Diakonikolas, Kane and Nelson 09: wise independence fools degree 2 PTFs. 8 -

Outline of Constructions Essentially a simplification halfspac 1. PRGs for regular PTFs of the hitting set of Rabani es. andhashing Shpilka. �Limited dependence �Berry-Esseen theorem and invariance principle 2. Reduce arbitrary PTFs to regular PTFs �Regularity lemmas and bounded independence 9 3. PRGs for logspace machines fool halfspaces

Regular Halfspaces All variables have low “influence”. Why regular? By CLT: Nice target distributions: • Enough to find G such that 10

Berry-Esseen Theorem Quantitative central limit theorem Error depends only on first four moments! Crucial for our analysis. 11

Toy Example: Majority Ø For simpliciy, let . Ø BET: For Ø Idea: Error in BET depends only on first four moments. Let’s exploit that! 12
![Fooling Majority Let Partition n into t blocks Block 1 Block t Observe Ys Fooling Majority Let Partition [n] into t blocks. Block 1 Block t Observe: �Y’s](https://slidetodoc.com/presentation_image_h/aff67132a3ddf2d88c825a4e92041118/image-13.jpg)
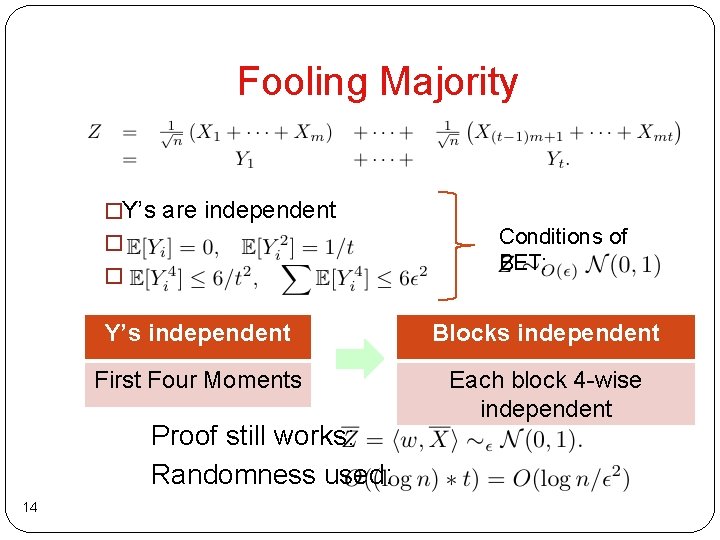
Fooling Majority Let Partition [n] into t blocks. Block 1 Block t Observe: �Y’s are independent � � 13 Conditions of BET:

Fooling Majority �Y’s are independent Conditions of BET: � � Y’s independent Blocks independent First Four Moments Each block 4 -wise independent Proof still works: Randomness used: 14

Fooling Regular Halfspaces Ø Problem for general regular: weights skewed in a block �Example: Ø Solution: partition into blocks at random �Analysis reduces to the case of majorities. �Enough to use pairwise-independent hash functions. Ø Some notation: �Hash family � 4 -wise independent generator 15

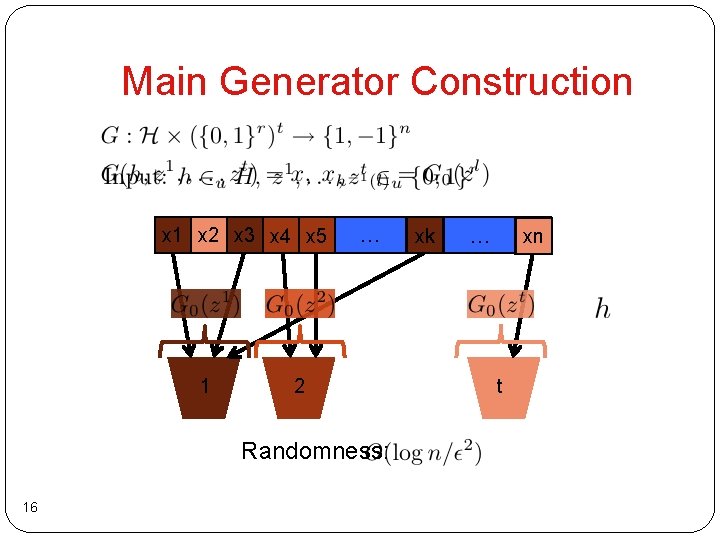
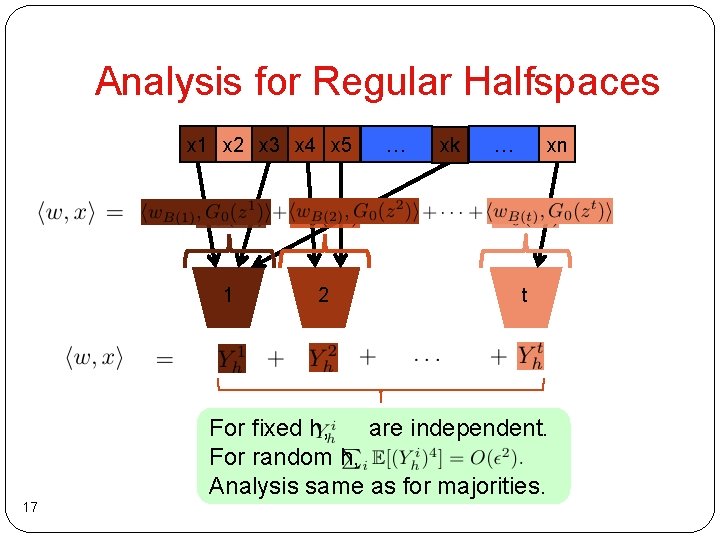
Main Generator Construction x 1 x 2 x 3 x 4 x 5 1 … 2 Randomness: 16 xk … xn t

Analysis for Regular Halfspaces x 1 x 2 x 3 x 4 x 5 1 2 … xk xn … t For fixed h, are independent. For random h, Analysis same as for majorities. 17

PRGs for Halfspaces 1. PRGs for Regular halfspaces �Limited dependence and Hashing �Berry-Esseen theorem 2. Reduction to regular case (Servedio, 2. Reduce arbitrary halfspaces to regular DGJSV): case ØHalfspace is regular – use previous �analysis Regularity lemmas and bounded Ø Halfspace depends only on few independence variables – use bounded independence. 18 3. PRGs for logspace machines fool halfspaces

Outline of PRGs for PTFs 1. PRGs for regular PTFs �Limited independence and hashing �Invariance principle of Mossel et al. [MOO 05] Same generator with stronger. Analysis more complicated: ØCannot use invariance principle as black box ØNew ‘blockwise’ hybrid argument 2. Reduce arbitrary PTFs to regular PTFs �Regularity lemmas of Diakonikolas et al. [DTSW 09], Harsha, Klivans, M. [HKM 09] 19

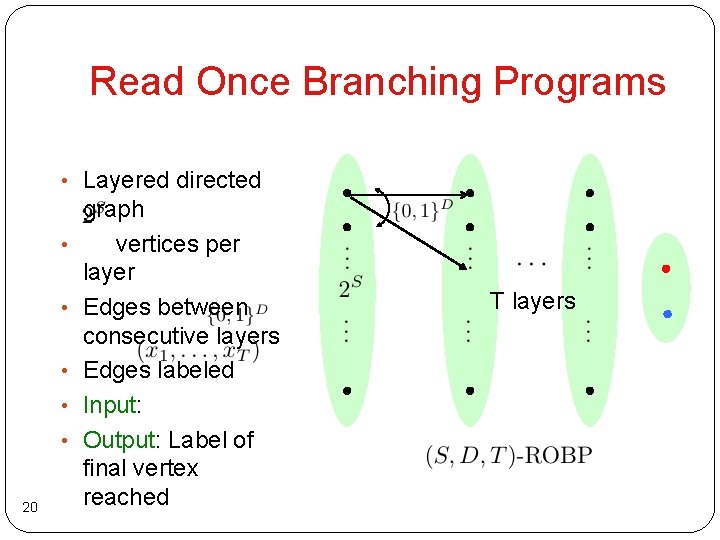
Read Once Branching Programs • Layered directed • • • 20 graph vertices per layer Edges between consecutive layers Edges labeled Input: Output: Label of final vertex reached T layers

PRGs for ROBPs Stretch r bits to n bits and “fool” (S, D, T)ROBPs. 21

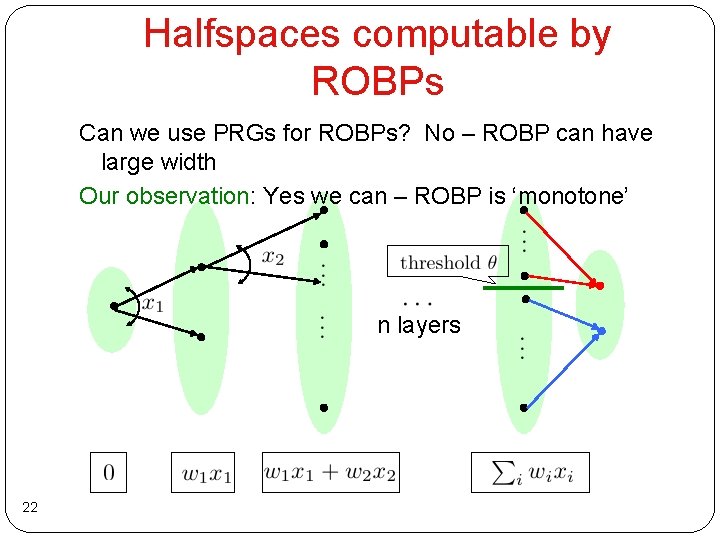
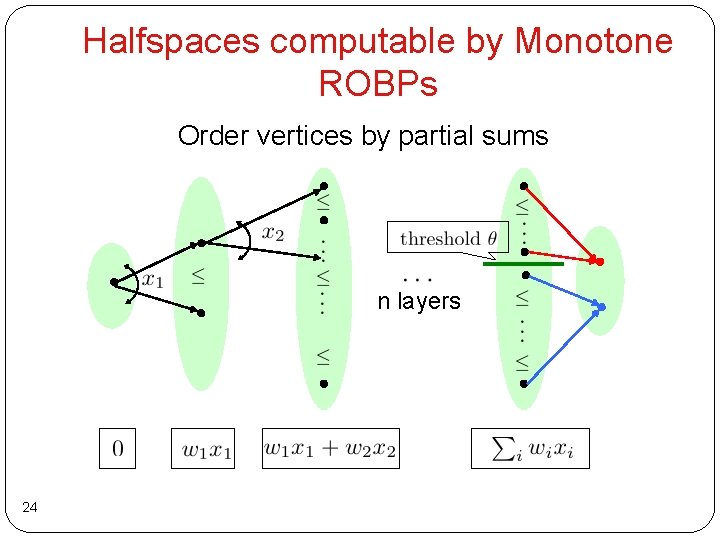
Halfspaces computable by ROBPs Can we use PRGs for ROBPs? No – ROBP can have large width Our observation: Yes we can – ROBP is ‘monotone’ n layers 22

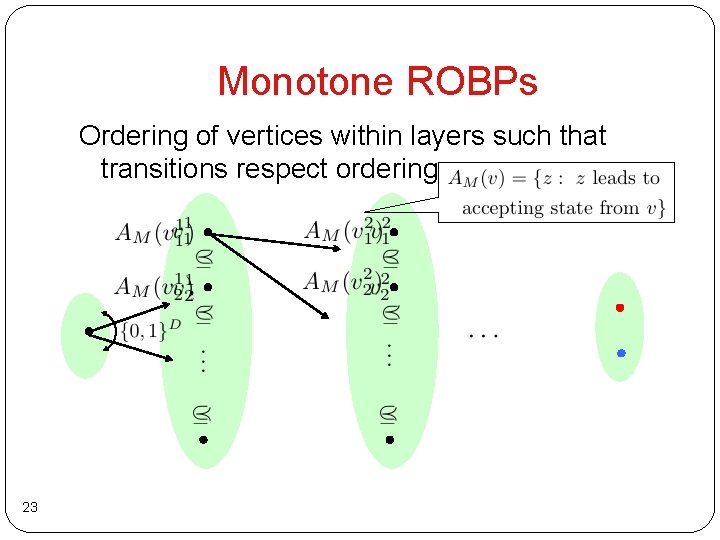
Monotone ROBPs Ordering of vertices within layers such that transitions respect ordering 23

Halfspaces computable by Monotone ROBPs Order vertices by partial sums n layers 24

Fooling Monotone ROBPs Monotone Trick: PRGs for small-width ROBPs fool arbitrary width monotone ROBPs. Thm: Cor: Nisan 90, INW 94 PRGs fool halfspaces with seed-length and error. Already improves previous constructions. 25

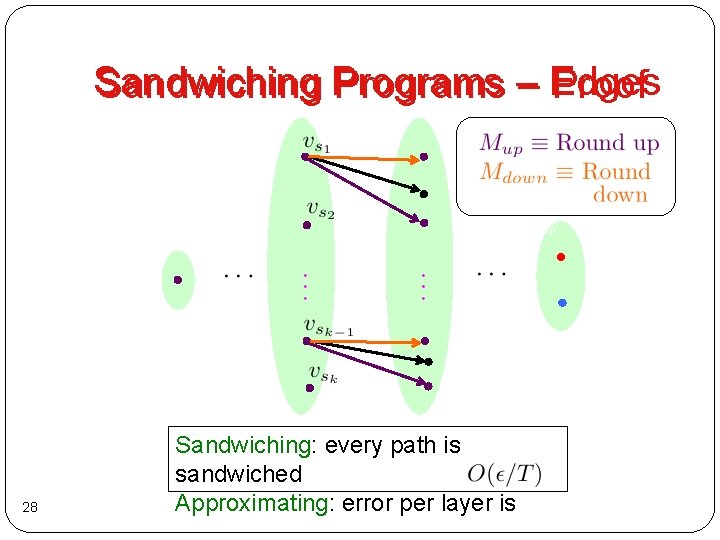
Proof via Sandwiching Pair of ROBPs for M if: -sandwiching � � Bazzi 2006: Existence of small-width sandwiching programs enough. 26

Sandwiching Programs Sparsification 27

Sandwiching Programs – Edges Proof 28 Sandwiching: every path is sandwiched Approximating: error per layer is

Summary for Halfspaces 1. PRGs for Regular halfspaces �Limited independence, hashing �Berry-Esseen theorem 2. Reduce arbitrary case to regular case �Regularity lemmas, bounded independence 3. PRGs for ROBPs fool Halfspaces 29 �More general ‘monotone trick’ PRG for Halfspaces
![Subsequent Work 30 Reference Gopalan et al GOWZ 09 Harsha et al HKM 09 Subsequent Work 30 Reference Gopalan et al. [GOWZ 09] Harsha et al. [HKM 09](https://slidetodoc.com/presentation_image_h/aff67132a3ddf2d88c825a4e92041118/image-30.jpg)
Subsequent Work 30 Reference Gopalan et al. [GOWZ 09] Harsha et al. [HKM 09 b] (new IP + generator) Result PRGs for functions of halfspaces under product distributions Quasi-polynomial time approx. counting for “regular” integer programs Gopalan et al. [GKM 10] Deterministic approximate counting for knapsack

Take Home … PRGs from invariance principles �IPs give us nice target distributions to aim. �Error depends on first few moments – manage with limited independence + hashing. Monotone trick �Width not important if more structure in ROBP. �PRGs of Nisan 90, INW 94 always more powerful than we know them to be. 31

Open Problems Better PRGs for PTFs? Optimal non-explicit: Possible approach: adapt monotone trick to work for higher degree PTFs. 32

Open Problems Optimal PRGs for Monotone ROBPs? Improving Nisan 90, INW 94 an outstanding open problem. Monotone ROBPs an important special case. 33

Open Problems More applications of ‘PRGs from invariance principles’? 34

Thank You 35