Efficient Pseudorandom Generators from Exponentially Hard OneWay Functions

Efficient Pseudorandom Generators from Exponentially Hard One-Way Functions Iftach Haitner, Danny Harnik, Omer Reingold 1

Pseudorandom Generators (PRG) [BM 82, Yao 82] Eff. computable function G: {0, 1}n ! {0, 1}n’ x n n G(x) Increases Length (n’ > n) Output is computationally indistinguishable from random. G(Un) w. C Un’ n Central in cryptography, implies bit-commitment [Naor 91], pseudorandom functions [GGM 86], pseudorandom permutations [LR 88] and … 2

PRG Based on General Hardness Assumptions One-way permutations [BM 82, Yao 82]. O(n) O(n 3) n Regular one-way functions [GKL 88]. n!{0, 1}n is a one-way function (OWF) if Def: f: {0, 1} n n is function n Any !{0, 1} one-way [HILL 89]. f: {0, 1} regular if all images have the O(n 8) n Efficiently computable same preimage size n it holds -1(f(x))| 2. for. Hard to invert: for any PPT n any x 2{0, 1} that |f = resulting n. Input Blowup: The ninput -1 length. Aof the PrxÃUn [A(f(x), 1 ) 2 fto(f(x))] = neg(n)OWF. PRG grows compared the underlying 1. • Central to the security of the construction. n, then it is If f is • also a permutation on {0, 1} denote the input length of the OWF by n a one-way permutation (OWP). 3

n!{0, 1} Example: We trustn ais. OWF to befunction secure Def: f: {0, 1} a one-way an exponentially hardonly for one-way 100 bitif: inputs. (OWF) function if: Efficiently computable n 1. [BMY] is insecure for seed < 100 bits. Hardistoinsecure invert: for anyseed PPT A< 1016 bits! n 2. [HILL] n -Cn n) 2 f-1 -1(f(x))] = PrxÃUn [A(f(x), 1 neg(n) < 2 xÃUn Goal: Reduce input length blowup. for some constant C> 0 n [Holenstein 06] One-way function with 5) O(n exponential hardness (2 -Cn for some C>0) 4

Our Results Paper [BM 82][Y 82] Restriction One-way Permutations Seed length n +o(n) [GKL 88] Regular OWF O(n 3) [HHR 05] Regular OWF O(n log n) [HILL 89] Any OWF O(n 8) [HHR 05] Any OWF O(n 7) [Holens 06] Exponentially Hard OWF O(n 5) This work Exponentially Hard OWF O(n 2) 5

PRG from exponentially hard OWF n [Holenstein 06] is a generalization of [HILL] that takes into account the hardness 2 -Φn length is a function Φ, with optimal results when Φ is a constant C. ¨ Seed n Our construction follows by developing the Randomized Iterate techniques presented in [HHR 05] in the context of PRGs from regular OWFs. ¨ Works only for Φ> Ω (1/log n) 6

Plan of the talk: Motivation - The BMY generator. n The Randomized Iterate. n A PRG from regular OWFs. n The randomized iterate of a general OWF. n The construction for exponentially hard OWFs. n 7

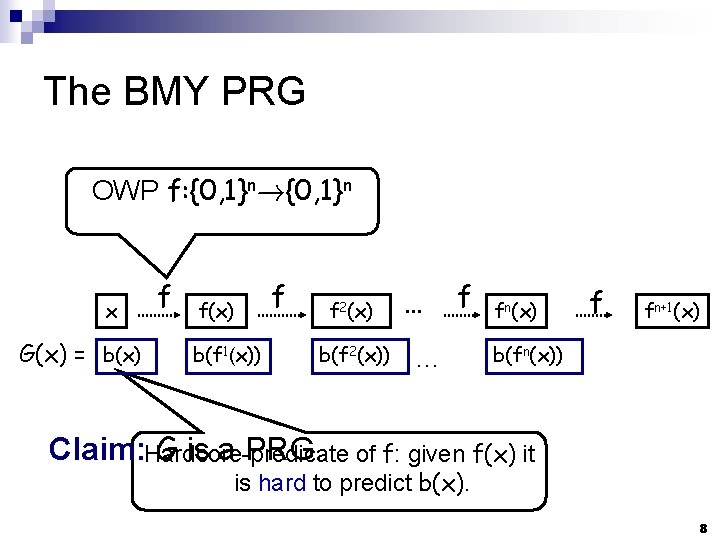
The BMY PRG OWP f: {0, 1}n!{0, 1}n x G(x) = b(x) f f(x) b(f 1(x)) f f 2(x) b(f 2(x)) … fn(x) f fn+1(x) b(fn(x)) Claim: Hardcore-predicate G is a PRG. of f: given f(x) it is hard to predict b(x). 8

given z = fk(x) it is hard to find y such that f(y) = z One-Way on Iterates: [Levin]: If 8 k it is hard to invert fk Then b(x), b(f(x)), …, b(fm(x)) is pseudorandom. 9

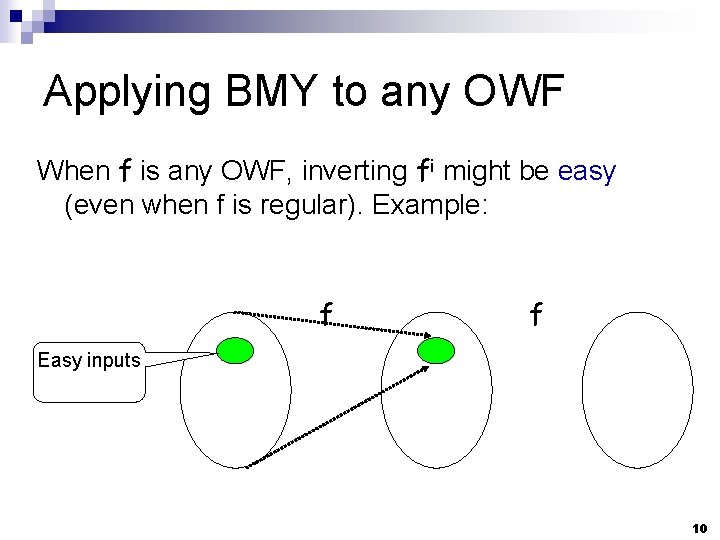
Applying BMY to any OWF When f is any OWF, inverting fi might be easy (even when f is regular). Example: f f Easy inputs 10

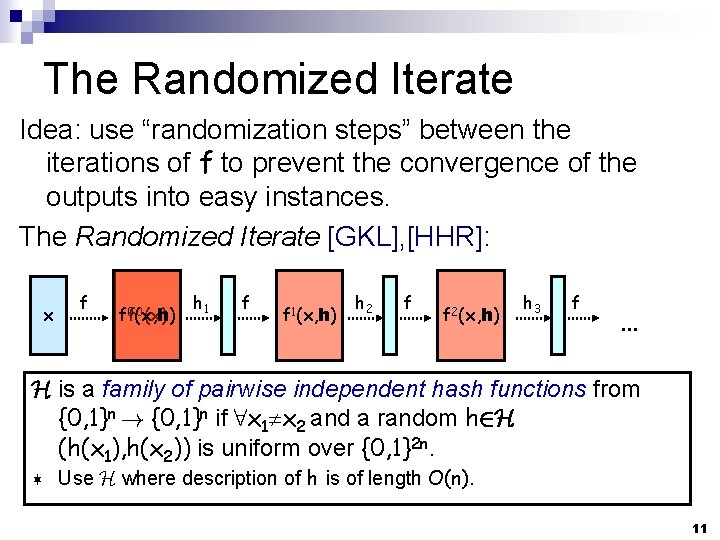
The Randomized Iterate Idea: use “randomization steps” between the iterations of f to prevent the convergence of the outputs into easy instances. The Randomized Iterate [GKL], [HHR]: x f 0(x) f 0 f(x, h) h 1 f f 1(x, h) h 2 f f 2(x, h) h 3 f h. H= is (h 1 a , . . . , h pairwise independent hash functions n) random family of pairwise hash functions {0, 1}n ! {0, 1}n if 8 x 1 x 2 and a random h 2 H 0(x, h)), . . . , b(f n(x, h)), h G(x, h) = b(f (h(x 1), h(x )) is uniform over {0, 1}2 n. 1, . . . , hn 2 ¬ … from Use H where description of h is of length O(n). 11

Lemma [HHR]: (Last randomized iteration is hard to invert) Let f be a regular OWF and H be family of pairwise independent hash functions, then no PPT can invert fk given h 1, . . . , hk. Corollary: Let f be a regular OWF and H be family of pairwise independent hash functions, then G(x, h) = b(f 0(x, h)), b(f 1(x, h)), …, b(fn(x, h)), h is a PRG. 12

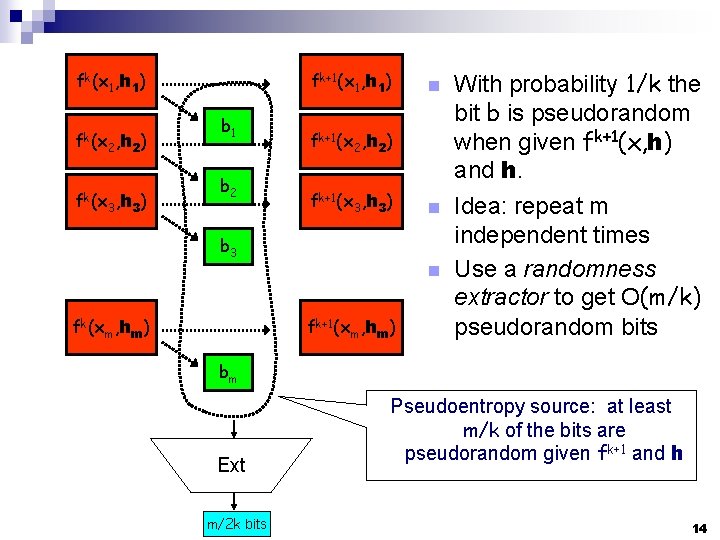
Randomized Iterate of general OWF Can we apply the construction to any OWF? ¨ No, security deteriorates with every iteration. Lemma: It is hard to invert fk (given h) over a set of density at least 1/k. (x, h) ! f 0(x, h), f 1(x, h) , … , fk(x, h) n n fk is hard to invert whenever the last iteration is at least as heavy as all the iterations in the sequence. By Symmetry happens with probability ¸ 1/k. Note: for regular functions always true… 13

k(x, h) ffk(x 1, h 1) fk(x 2, h 2) fk(x 3, h 3) k+1 ffk+1 (x (x, h) 1, h 1) bb 1 b 2 n fk+1(x 2, h 2) fk+1(x 3, h 3) n b 3 n fk(xm, hm) fk+1(xm, hm) With probability 1/k the bit b is pseudorandom when given fk+1(x, h) and h. Idea: repeat m independent times Use a randomness extractor to get O(m/k) pseudorandom bits bm Ext m/2 k bits Pseudoentropy source: at least m/k of the bits are pseudorandom given fk+1 and h 14

Randomness Extractors [NZ 93] n n n Extract randomness from distributions which contain sufficient (min)-entropy. Use a short seed of truly random bits. Output is (close to) uniform even when the seed is known. n n high pseudoentropy distribution high entropy distribution Extractor seed pseudorandom output Uniform extraction Lemma: an analogues result for pseudoentropy, appears implicitly in [HILL] New proof of the uniform extraction Lemma given in [Holens 06] & [HHR 05]. ¨ Based on the uniform hardcore set proof of Holenstein (FOCS 2005). 15

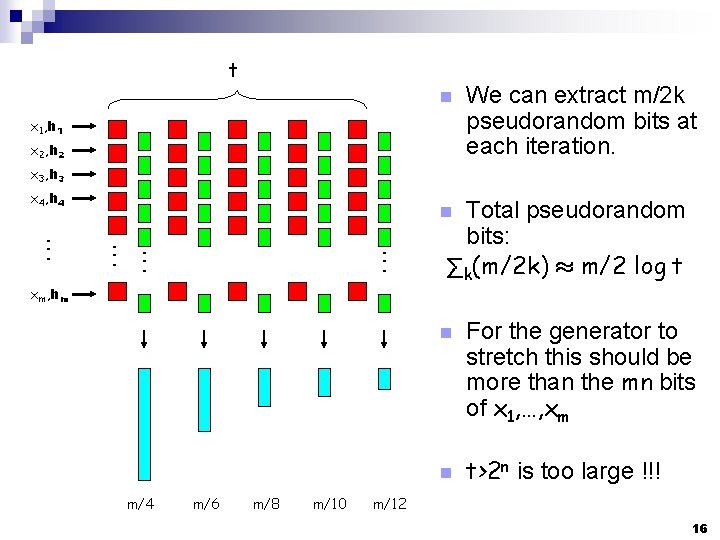
t n x 1, h 1 x 2, h 2 We can extract m/2 k pseudorandom bits at each iteration. x 3, h 3 x 4, h 4 Total pseudorandom bits: ∑k(m/2 k) ¼ m/2 log t n xm, hm n n m/4 m/6 m/8 m/10 For the generator to stretch this should be more than the mn bits of x 1, …, xm t>2 n is too large !!! m/12 16

Exponential hardness Theorem [GL 89]: if a one-way function f has hardness 2 -Cn then it has O(Cn) hard-core bits. We can take out more pseudorandom bits at every iteration! 17

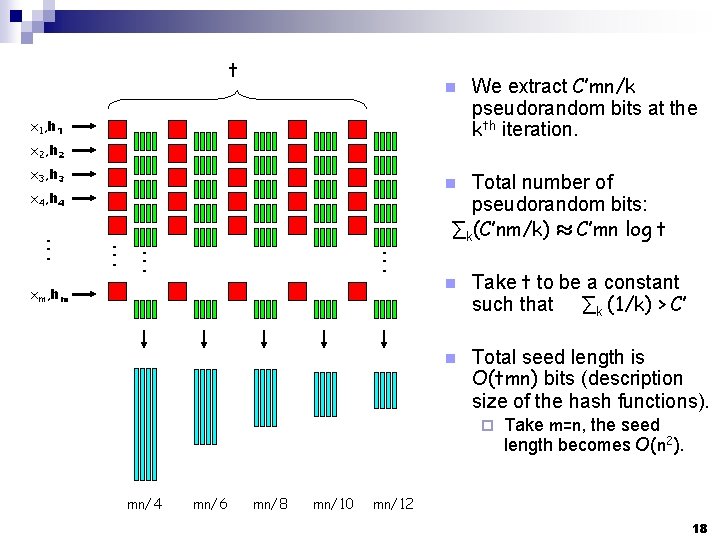
t n x 1, h 1 x 2, h 2 x 3, h 3 Total number of pseudorandom bits: ∑k(C’nm/k) ¼ C’mn log t n x 4, h 4 We extract C’mn/k pseudorandom bits at the kth iteration. xm, hm n n Take t to be a constant such that ∑k (1/k) > C’ Total seed length is O(tmn) bits (description size of the hash functions). ¨ mn/4 mn/6 mn/8 mn/10 Take m=n, the seed length becomes O(n 2). mn/12 18

Questions and Further Issues n n Holenstein achieves seed O(n 4 log 2 n) if the resulting PRG need only have standard hardness (superpolynomial). Accordingly, we get O(n log 2 n) in such a case. Can such methods work for general OWFs? n n Could work if the deterioration in security in each iteration where somehow limited. Other applications of exponentially hard OWFs? n Recent results of [GI 06], [HR 06]. 19