Normal Forms Western Michigan University CS 6800 Advanced

Normal Forms Western Michigan University CS 6800 Advanced Theory of Computation Spring 2014 By Abduljaleel Alhasnawi & Rihab Almalki

Introduction » Grammar: G = (V, , R, S) Terminals and Nonterminals Terminals V = {A, B, C , a , b, c} = { a, b } Start Symbol S Rules R=S→A

Regular Grammar » Rules: X Y , where: » X V- » Ex: S a. S » Y : , a, A, a. B » G 1: R= S a. S | . . . ? » G 2: R= S a. Sa | b. Sb | . . ? » G 3: R= S SS | (S) | . . . ?

Context Free Grammar (CFG) » Rules: X Y , where: » X V- and |X| = 1 » Ex: S a. S » Y V* » Ex: S S a. Sb » A a A b. BBa » A B S SS » A a. B S ABCD

Ambiguity » A grammar G is ambiguous iff there is at least one string in L(G) for which G produces more than one parse tree. » Ex: » Bal = { w {), (}*: the parentheses are balanced} » G = {{S, ), (}, {), (}, R, S} , where: » R = S SS | (S) |

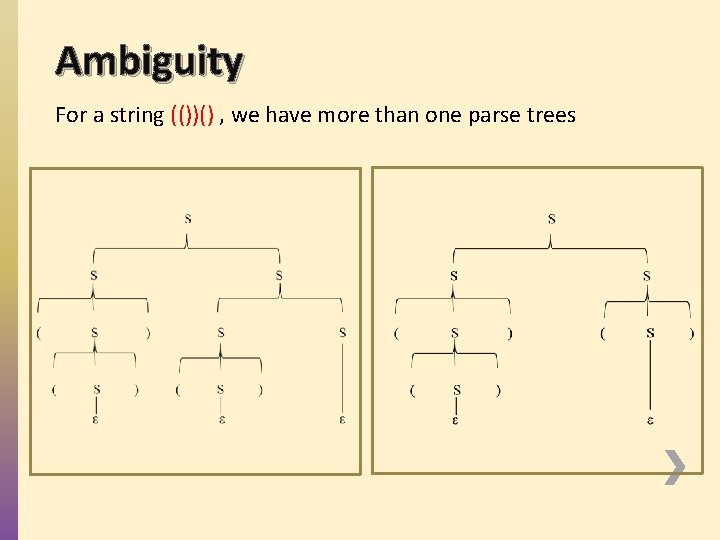
Ambiguity For a string (())() , we have more than one parse trees

Normal Forms » Chomsky Normal Form (CNF) » Def. : A context-free grammar G = (V, Σ, R, S) is said to be in Chomsky Normal Form (CNF), iff every rule in R is of one of the following forms: » X a where a , or » X BC where B and C V- » Greibach Normal Form (GNF) » Def. : GNF is a context free grammar G = (V, , R, S), where all rules have one of the following forms: » X a where a and (V- )*

Converting to Chomsky Normal Form » There exists 5 -steps algorithm to convert a CFG G into a new grammar Gc such that: L(G) = L(Gc) – { } » convert. Chomsky(G: CFG) = » 1 - G' = remove. Eps(G: CFG) S » 2 - G'' = remove. Units(G': CFG) A B » 3 - G''' = remove. Mixed(G'': CFG) A a. B » 4 - G'v = remove. Long(G''' : CFG) S ABCD » 5 - G'v : L(G) = L(G'v) – { } Gv = atmostone. Eps(G'v: CFG) S* S, S

Remove Epsilon » » » Find the set N of nullable variables in G. X is nullable iff either X or (X A , A ) : X Ex 1: G: S a. ACa A B|a B C|c C c. C | Now, since C , C is nullable since B C , B is nullable since A B , A is nullable Therefore N = { A, B, C}

Remove Epsilon » According to N, the rules will be: » S a. ACa » A B|a| » B C|c| » C c. C | » Now, remove. Eps returns G': » S a. ACa | a. Aa | a. Ca | aa » A B|a » B C|c » C c. C | c

Remove Unit Productions » Def. : unit production is a rule whose right hand side consists of a single nonterminal symbol. Ex: A B » Remove any unit production from G'. » Consider the remain rules » Ex 1(continue), G‘: » S a. ACa | a. Aa | a. Ca | aa » A B|a » B C|c » C c. C | c

Remove Unit Productions » » » » » Now by apply remove. Units(G': CFG) : Remove A B But B C | c, so Add A C | c Remove B C Add B c. C (B c, already there) Remove A C Add A c. C (A c, already there) So remove. Units returns G'' : S a. ACa | a. Aa | a. Ca | aa A a | c. C B c | c. C C c. C | c

Remove Mixed » Def. : mixed is a rule whose right hand side consists of combination of terminals or terminals with nonterminal symbol. » Create a new nonterminal Ta for each terminal a » For each Ta , add the rule Ta a » Ex 1(continue), G'' : » S a. ACa | a. Aa | a. Ca | aa » A a | c. C » B c | c. C » C c. C | c

Remove Unit Productions » Now, by apply remove. Mixed(G'': CFG), G''' : » S Ta. ACTa | Ta. ATa | Ta. CTa | Ta. Ta » A a | c | Tc C » B c | Tc C » C Tc C | c » Ta a » Tc c

Remove Long » Def. : long is a rule whose right hand side consists of more than two nonterminal symbol. » R: A BCDE » By remove long, it will be: » A BM 2 » M 2 CM 3 » M 3 DE » Ex 1(continue), G'' : » S a. ACa | a. Aa | a. Ca | aa » A a | c. C » B c | c. C » C c. C | c

Remove Long » Ex 1(continue), G''' : » S Ta. ACTa | Ta. ATa | Ta. CTa | Ta. Ta » A a | c | Tc C » B c | Tc C » C Tc C | c » Ta a » Tc c

Remove Long » Now, by apply remove. Long(G''' : CFG), G'v : » » » » S Ta. S 1 |Ta. S 3 |Ta. S 4 |Ta. Ta S 1 AS 2 CTa S 3 ATa A a | c | T c. C B c | T c. C C Tc C | c Ta a Tc c S 4 CTa

Add Epsilon » Finally, atmostone. Eps(G'v: CFG) does not apply in Ex 1, Gv = G'v since L does not contain (S is not » » » » nullable). S Ta. S 1 |Ta. S 3 |Ta. S 4 |Ta. Ta S 1 AS 2 CTa S 3 ATa A a | c | T c. C B c | T c. C C Tc C | c Ta a Tc c S 4 CTa

Example 2 » Convert the following CFG to CNF: » S ABC » A a. C | D » B b. B | | A » C Ac | | Cc » D aa

1 -Remove epsilon » » » » » N = {A, B, C} So add S AB|BC|AC, A a, B b, C c delete B , C The result is: S ABC| AB|BC|AC A a. C | D|a B b. B | A|b C Ac | Cc| c D aa

2 - Remove units » S ABC| AB|BC|AC » A a. C | D |a (A D, D aa) remove A D add A aa » B b. B | A|b (B A, A a. C|aa|a) remove B A add B a. C|aa|a » C Ac | Cc|c » D aa

2 - Remove units » S ABC| AB|BC|AC » A a. C | aa |a » B b. B | a. C|aa|a|b » C Ac | Cc|c » D aa

3 - Remove Mixed » S ABC| AB|BC|AC » A Ta. C | Ta. Ta |a » B Tb. B | Ta. C| Ta. Ta |a|b » C ATc | CTc|c » D T a

4 - Remove Long » » » » » S AM 2| AC|AB M 2 BC A Ta. C | Ta. Ta |a B Tb. B | Ta. C| Ta. Ta |a |b C ATc | CTc|c D T a Ta a Tb b Tc c

5 - Add Epsilon: N/A » » » » » S AM 2| AC|AB M 2 BC A Ta. C | Ta. Ta |a B Tb. B | Ta. C| Ta. Ta |a |b C ATc | CTc|c D T a Ta a Tb b Tc c

Example 3 » » » » » Convert the following CFG to CNF: A → BAB | ε B → 00 | ε 1 - remove epsilon: A → BAB | BB | AB | BA B → 00 2 - remove units: A → BAB | 00 | BB | AB | BA B → 00

» 3 - remove mixed » A → BC | T 0 T 0 | BB | AB | BA » C → AB, B → T 0 T 0, T 0 → 0 » 4 - Add epsilon » A → BC | T 0 T 0 | BB | AB | BA | » C → AB » B → T 0 » T 0 → 0

Example 4 » Which one is Chomsky Normal Form ? Why?

Chomsky Normal Form Not Chomsky Normal Form

Example 5 » Convert the following CFG to CNF:

Introduce new variables for the terminals:

Introduce new intermediate variable to break first production:

Introduce intermediate variable:

Final grammar in Chomsky Normal Form: Initial grammar

Example 6 » » » » Convert the following CFG to CNF: E E+T E T T T F F (E) F id

1 - Remove units » » » » Remove E T , add E T F |F Remove E F , add E (E) | id Remove T F , add T (E) | id The result: E E + T | T F | (E) | id T T F | (E) | id F (E) | id

2 - Remove Mixed » » » » E E T+ T | T T F | T(E T)| id T T T F | T(E T)| id F T(E T)| id T( ( T ) ) T+ + T* *

3 - Remove Long » » » » » E E M 2 | T M 3 | T( M 4 | id T T M 3 | T(M 4 | id F T( M 4 | id M 2 T+ T M 3 T* F M 4 E T) T( ( T ) ) T+ + T* *

5 - Add Epsilon: N/A » » » » » E E M 2 | T M 3 | T( M 4 | id T T M 3 | T(M 4 | id F T( M 4 | id M 2 T+ T M 3 T* F M 4 E T) T( ( T ) ) T+ + T* *

References » Elaine A. Rich (2008) Automata, Computability, and Complexity: Theory and Applications, Pearson Prentice Hall. » https: //cs. wmich. edu/~elise/courses/cs 680/pres entations. htm